基于梯度的等效静载荷法的汽车正面碰撞关键结构优化设计

陈 涛 戴江璐 陈自凯 李奇奇 李 卓

湖南大学汽车车身先进设计制造国家重点实验室，长沙,410082

基于梯度的等效静载荷法的汽车正面碰撞关键结构优化设计

陈 涛 戴江璐 陈自凯 李奇奇 李 卓

湖南大学汽车车身先进设计制造国家重点实验室，长沙,410082

针对在已有车型的继承式开发中，由于结构尺寸、总布置等因素限制，无法快速准确地进行结构非线性优化设计的问题，提出了一种基于梯度的等效静载荷法与G1-G2设计规则以及载荷传递路径相结合的正面碰撞关键结构优化设计流程：收集对标车型数据，根据G1-G2设计规则，确定满足乘员损伤的最优目标加速度等效双阶梯形波；建立载荷数据库，得到一类车型的碰撞载荷路径百分比分布图；提取基础车型正面碰撞关键部件，以目标波形为指导对其进行必要的截面尺寸优化，并运用ESLMG对其进行厚度优化；将优化后的关键部件放入整车模型中,验证其加速度曲线是否达到目标值。结果表明，优化后的结构特性基本达到目标要求，整车碰撞性能得以改善。

结构非线性优化；基于梯度的等效静载荷法；G1-G2设计规则；碰撞载荷路径；车身结构平台化

0 引言

近年来，许多汽车企业为了节约成本，缩短开发周期，致力于针对已有车型进行继承式开发，实现车身结构平台化建设[1]。但是，通常由于结构尺寸以及总布置等因素影响，无法快速准确地对结构进行有效的优化设计，尤其是针对非线性工况下的整车被动安全性能的提升，困难重重[2]。

车辆正面碰撞的减速度-时间曲线是碰撞动态非线性工况下最易获取且最具表征意义的响应特性之一，并且与乘员损伤存在密切关联[3]。在传统的车身抗撞性开发流程中，结构详细设计阶段通常是根据经验设计结构，对设计后的结构通过试验或虚拟试验方法进行验证，若碰撞波形没有得到改善，则需要再次修改结构，直至波形得到改善。该设计方法缺乏明确的目标指导，通常需要经历一个反复“试错”的过程[4]，工作量大、效率低、周期长，在继承式开发过程中无法为车身结构优化设计提供及时且有效的改进方案。

另外，对于汽车碰撞，由于结构非线性的存在，使得有限元仿真模型的计算是非常“昂贵”的。在运用传统的设计方法进行结构耐撞性优化设计时，由于碰撞分析的非线性效应，使得灵敏度的计算代价太高[5-7]。Kang等[8]针对动态线性优化问题而提出的等效静载荷法(equivalent static loads method，ESLM)，将求解耗时、收敛性差和计算复杂的动态优化问题，转化为技术成熟的线性静态优化问题，与传统的基于梯度的数值优化算法和全局优化算法相比，该方法可以极大地提高优化效率。Shin等[9]提出了基于等效静载荷求解静态非线性优化问题的方法，首次考虑了结构的非线性特性。陈涛等[10]扩充了等效静载荷的概念，同时考虑了动态效应和非线性特性，可以求解动态非线性优化问题。然而，当结构的非线性很显著或设计变量较多时，非线性分析与线性分析的差异会增大，ESLM优化效率会降低。朱航斌等[11]提出了一种基于梯度的等效静载荷法(ESLM based on gradient, ESLMG)，该方法对于处理大变形及多变量结构动态非线性优化问题非常有效，同时该方法在收敛速度方面相比ESLM方法和数值优化算法具有很大的优势。

本文突破传统有限元试错法的盲目性与局限性，首先确立满足乘员损伤要求的高性能减速度-时间曲线，以指导结构优化的方向和目标。然后，通过分析载荷传递路径分布情况，选择关键部件作为优化对象并对其进行必要的截面尺寸优化，充分利用基于梯度的等效静载荷法(ESLMG)的稳健性、可靠性和高效性对截面厚度进行快速优化，达到目标曲线的优化设计要求。基于ESLMG的正面碰撞关键结构优化设计流程如图1所示。

图1 基于ESLMG的正面碰撞关键结构优化设计流程

1 结构耐撞性优化目标确定

综合学术界和工业界对碰撞过程的已有理解，把整车碰撞减速度-时间历程设为车身结构优化设计的目标量值是合理而有效的[3]。

基于能量守恒原理的两阶(G1-G2)等效波形可以有效替代复杂的实车波形，两阶波形可以为整车碰撞波形规划提供有效的指导，为工程化阶段结构碰撞性能提供评价手段[12]。等效双阶梯形波的两阶特性是由于发动机参与碰撞引起的。车体前部结构可以简化成图2所示的几个区域，其中，D1为发动机在发生碰撞之前的压缩距离，D2为发动机发生碰撞之后可利用的压缩空间。实车测取D1，取发动机发生碰撞的时间为T1，以T1为界将减速度时间曲线分为G1和G2两大区域。

图2 前端结构主要尺寸简图

在G1和G2两大区域中，用等效梯形波代替减速度曲线的方法称为“G1-G2设计规则”。其中，车体碰撞速度：

(1)

车体碰撞减速度：

(2)

由式(1)和式(2)可以得到

adx=vdv

(3)

adx或vdv称为能量密度微分，将式(3)两端积分有

(4)

在G1区域设减速度为恒定G1，边界条件有：t=0,x=x0=0,v=v0(碰撞初速度)；t=T1,x=D1,v=vD1(T1时刻车体速度)。将上述条件代入式(4)中，有

(5)

同理在G2区域：t=T1,x=x0=D1，v=v0=vD1；t=tm,x=C,v=0。可得

(6)

式中，C为整车压溃距离。

与概念设计中采用的方法类似，在已有基础车型的继承式开发过程中，同样可以通过对标分析(benchmarking)结果来制订结构性能优化目标，重新定位车身结构的安全性能。耐撞性对标分析的任务是：根据竞争对手车型的碰撞减速度曲线制订出自己的G1-G2目标域[3]。图3给出了5个参考车型的减速度-时间历程曲线，根据“G1-G2设计规则” 计算得到各对标车型的等效双阶梯形波的G1和G2值，将它们简化成等效双阶梯形波，并形成包络线如图4所示。本文选用的基础车型的加速度曲线及其简化波形如图5所示，其中，G1=16g,G2=39g，参照包络线范围，可得到一系列加速度波形，分别为等效波形：16g/39g(基础车型)、14g/42g、18g/35g、20g/32g。根据MADYMO乘员损伤值的计算结果，优化选择一组G1/G2作为基础车型结构优化的目标曲线[13]。

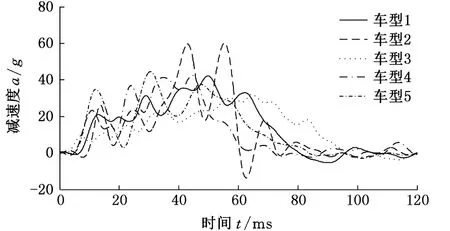
图3 对标车型减速度-时间曲线

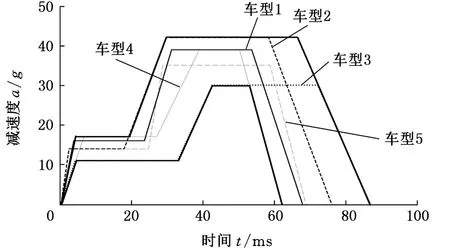
图4 等效双阶梯形波包络线

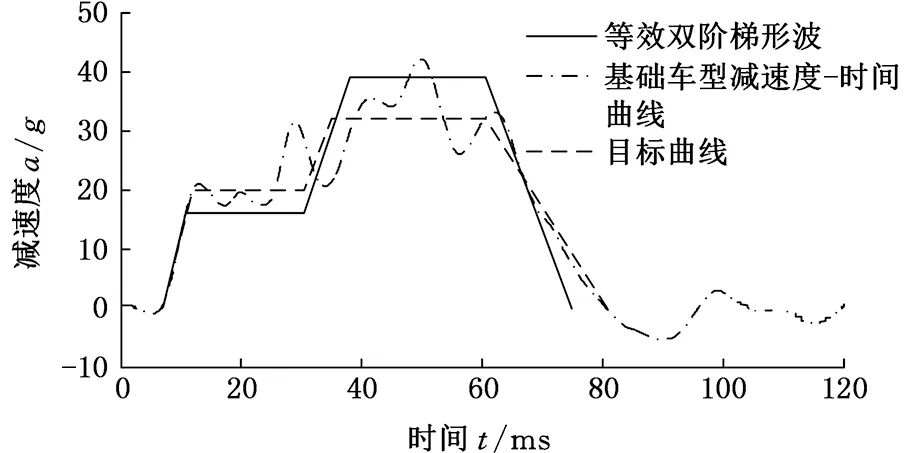
图5 基础车型加速度曲线及其简化波形

如表1所示，利用MADYMO/Toolbar计算得到的约乘效率、假人胸部3 ms加速度峰值变化、C-NCAP评分等结果，可以看出，G1=20g，G2=32g的两阶波形为各项指标结果最佳的方案，故定义该等效双阶梯形波为优化设计的目标波形。

表1 乘员约乘效率、胸部加速度及C-NCAP评分

2 关键结构提取与简化模型的建立

2.1 碰撞载荷传递路径

收集并计算得到前文提到的5款竞争车型(整备质量为1.0～1.4 t，整车长度为4.2～4.8 m，前置前驱的家用轿车)的前端结构关键截面碰撞载荷数据如表2所示。经过数据分析与处理，得到车辆前端结构载荷分配百分比如图6所示。

表2 竞争车型截面碰撞载荷数据 kN

图6 前端结构碰撞载荷百分比分布

可以看出，前纵梁及其前端吸能结构在正面100%碰撞工况下的载荷传递路径上承担了绝大部分载荷，对整车碰撞安全性能起到了决定性的作用。基础车型的仿真和试验结果显示，前纵梁中后段吸能较低，且设计空间受总布置约束很大，所以本文仅提取基础车型纵梁前端及吸能盒所在子系统作为结构优化设计对象，着重对其截面进行优化设计并验证其有效性。

2.2 简化模型的建立及验证

本文采用简化模型代替整车模型以满足后续优化要求，同时，简化模型还可以缩短计算时间，提高计算效率。通过对整车碰撞模型的变形特征和吸能特性进行研究，建立了图7所示的前端结构碰撞的简化模型，模型中只保留了前防撞梁、吸能盒、前纵梁以及发动机总成，共有56 001 个节点，57 283 个单元。同时定义了一个集中质量点，且通过刚性单元与前端结构截断处的节点连接起来，以保证简化模型的重量和重心与原车一致。

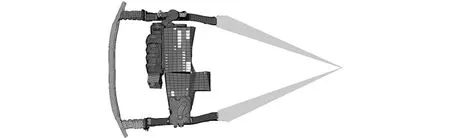
图7 前部碰撞关键子系统简化模型(俯视图)

由于前舱中防撞横梁与发动机前端的其他附件被省略，所以可能会对吸能盒与前纵梁的受力以及吸能情况产生一定的影响，而从上文的碰撞载荷传递路径分析可知，这个影响几乎是可以忽略不计的。

此外，由于简化模型省去了B柱等结构，所以在对模型计算精度进行验证时，无法直接读取B柱下方加速度与原始模型进行对比，因此需首先验证整车仿真模型与试验模型加速度曲线是否一致，再将验证后的整车仿真模型与简化模型的前端吸能结构的变形模式进行对比验证。

由图8、图9可以看出，整车试验曲线与仿真曲线变化趋势一致，加速度曲线的峰值时刻与大小基本相同，数据一致性较好；简化模型与整车模型在第一阶时间域内的变形模式也基本一致，所以简化模型计算结果的准确性和有效性得到保证，模型精度可以满足后续研究要求。

图8 整车试验与仿真减速度-时间曲线

3 前端关键吸能结构优化设计

本文将从两方面对前端关键吸能结构进行结构优化设计：一方面，先以G1/G2特征参数为目标，对其进行必要的截面形状优化，使其具有更佳的吸能特性的同时，减小质量，为后续的厚度优化提供更有利的优化空间；另一方面，运用基于梯度的等效静载荷法对该结构进行厚度优化，以进一步提高其耐撞性能，最终达到目标曲线优化设计目标，这是本文的主要目的所在。

3.1 截面形状优化

由于渐变的前小后大的截断的锥体结构在碰撞中更具稳定性[13]，所以首先利用hypermorph将原车型的吸能盒结构由等截面更改为渐变截面，如图10所示，更改后前端截面面积为后端截面面积的1/2，总质量较之前降低了13.3%。将更改后的吸能盒代入原车模型中验证结构吸能特性以及整车减速度-时间曲线。

(a)原始吸能盒(b)渐变截面吸能盒

表3数据表明，更改后的前小后大的吸能盒结构不仅质量减小了，而且平均碰撞力也增大了10.85%，吸收的能量增加了11.85%，具备更好的吸能能力。图11为更改后的减速度-时间曲线与其等效双阶梯形波，此时，G1=18g，G2=36g，G1值得到一定程度提升，但与目标曲线仍存在差距，需进一步优化。

表3 吸能盒形状优化前后吸能性能对比

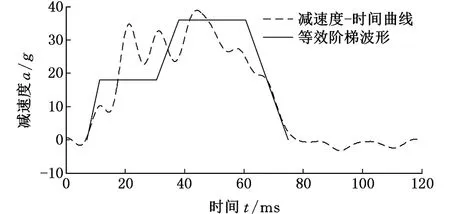
图11 截面优化后的减速度-时间曲线及其简化波形

3.2 ESLMG在吸能结构厚度优化中的应用

3.2.1 等效静载荷的概念

基于节点位移等效的等效静载荷定义为：在每个时间步，产生与动态非线性分析相同位移响应的、针对线性分析的静态载荷[10]。等效静载荷的概念如图12所示。在动态非线性分析的每个时间步(ti)，都产生一个等效载荷集(si)，时间步的总数与等效静载荷集的总数相等，静态响应曲线和动态响应曲线也是等效的。第i个时间步的结构阻尼效应和质量效应可以通过等效静载荷计算的节点位移来体现。从某种程度上说，等效的不只是位移，同时还包括了非线性特性与动态效应。

图12 等效静载荷概念

3.2.2 ESLMG基本思想与优化流程

图13 ESLMG基本思想

3.2.3 前端吸能结构厚度优化

在截面形状优化的基础上，运用ESLMG对吸能盒以及前防撞梁、前纵梁进行厚度优化，以进一步提高关键吸能结构的吸能特性，实现目标波形第一阶加速度G1值的提升。

本文吸能盒的结构优化设计采用连续变截面(tailor rolled blanks，TRB)技术，如图14所示，将吸能盒外板离散成5个部分并赋予其不同的厚度值，通过优化部件的厚度近似得到吸能盒以及其前纵梁前部的最佳厚度分布。

图14 参与厚度优化的部件

该问题是一个多变量非线性动态结构优化问题，约束前纵梁后端节点6个自由度，将前防撞横梁7，吸能盒1～6以及前纵梁内板8和外板9共9个部件的厚度作为设计变量。目标函数为吸能盒与前纵梁吸收的最大应变能U，通过优化设计变量使得最大应变能最大，约束d1和d2不超过各自的允许值，设置d1allow为d1的极限厚度，它是为了保证吸能盒在压溃时更充分地吸能，设置d2allow为d2的极限厚度，它是为了防止前纵梁过度压溃。图15所示为厚度优化前的前端结构有限元模型，刚性墙的质量设为800 kg，初始速度为50 km/h。

图15 前端结构有限元模型

该优化问题的数学模型如下：

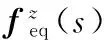
用ESLMG的方法对该问题进行优化，经过40次迭代收敛。最优解满足位移约束条件，同时使得应变能达到最大值。

为了证明该方法的有效性，针对以上问题，与全局最优化算法模拟退火算法(ASA)的优化结果进行对比，图16所示为两种方法优化后的厚度分布情况，可以看出，两种方法优化后的设计变量的取值基本相同，各个设计变量的偏差均不超过5%；表4结果显示，两种方法优化后的最大应变能基本一致，最大约束偏差均不超过3%；两种方法均达到了收敛条件。ESLMG相比ASA在计算效率上有较大的提升，CPU运算总时间缩短了93%。

图16 ASA与ESLMG优化后厚度分布

表4 ASA与ESLMG优化结果对比

4 整车验证与分析

将更改后的吸能盒结构以及优化后得到的各个部件的厚度分别更新并放入整车模型中，计算后得到正面100%碰撞工况下的整车加速度曲线与原始车型减速度-时间曲线(图17)，将其简化成等效双阶梯形波(图18)，优化后的第一阶加速度得到显著提高，G1值为19g，G2值为34g，基本达到目标要求，说明本文所采用的优化分析思想对于已有车型的继承式开发中结构优化设计是行之有效的。

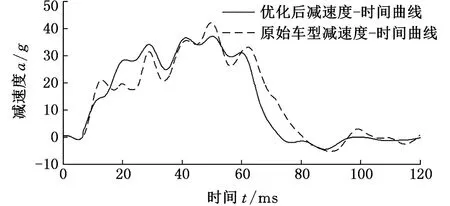
图17 优化前后整车减速度-时间曲线

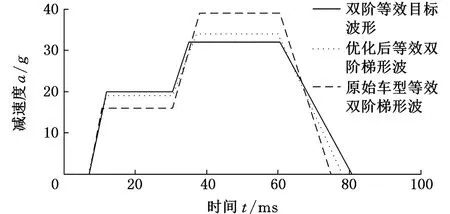
图18 优化前后等效双阶梯形波

5 结论

(1)根据G1-G2设计规程，形成了碰撞减速度-时间等效双阶梯形波的包络线，为基础车型的目标曲线确定了可行范围。结合MADYMO乘员损伤值计算结果，优化选择出最佳的G1和G2值，提供了明确的结构优化目标。同时验证了“提高第一阶加速度和降低第二阶加速度有利于减少乘员损伤”结论的正确性。

(2)运用一种基于梯度的等效静载荷法(ESLMG)对前端吸能结构的厚度进行了快速有效的优化。将优化结果与模拟退火算法(ASA)进行了对比，充分显示了ESLMG计算效率的优越性。

(3)将优化后的吸能结构在整车模型中进行计算验证，第一阶加速度G1值基本达到目标曲线设定要求，证明了本文提出的优化设计思想以及ESLMG算法对于已有车型继承式开发正面碰撞关键结构优化设计中，解决大变形和多变量结构动态非线性优化问题的有效性。

[1] 鞠晓锋. 车身平台化开发策略研究[J].汽车技术，2012(2)：7-10. Ju Xiaofeng, Study of BIW Platform Development Strategy[J]. Automotive Technology，2012(2)：7-10.

[2] 袁焕泉. 车身平台开发与关键技术研究[J]. 大众汽车，2014,20(8)：32-39. Yuan Huanquan. Study on Auto-body Platform and Key Technology[J]. Popular Auto, 2014,20(8)：32-39.

[3] 唐洪斌. 乘用车正面耐撞性方法研究[D]. 长春：吉林大学，2008.

[4] 刘乐丹.某乘用车正面碰撞波形优化及其方法研究[D].长春：吉林大学，2011.

[5] Park G J. Analytical Methods in Design Practice[J]. Journal of AIAA, 2012，10：636-649.

[6] Arora J S. Introduction to Optimum Design[J]. Elsevier, 2004, 2(1) ：114-161.

[7] Haftka R T, Gurdal Z. Elements of Structural Optimization[M]. Dordrecht: Kluwer Academic Publisher, 1992.

[8] Kang B S, Choi W S, Park G J. Structural Optimization under Equivalent Static Loads Transformed from Dynamic Loads Based on Displacement[J]. Comput. Struct.， 2001, 79 (2):145-154.

[9] Shin M K, Park K J, Park G J. Optimization of Structures with Nonlinear Behavior Using Equivalent Loads[J]. Comput. Methods Appl. Mech. Engrg., 2007, 196(2):1154-1167.

[10] 陈涛，陈自凯，段立斌，等.针对结构动态非线性优化问题的ESLM梯度优化方法[J].机械工程学报，2014,50(6)：1-9. Chen Tao, Chen Zikai, Duan Libin，et al. Gradient-based Equivalent Static Loads Method for Structure Nonlinear Dynamic Optimization Problem[J]. Journal of Mechanical Engineering, 2014,50(6):1-9.

[11] 朱航斌，刘学军. 正面碰撞波形对乘员伤害值的影响[J]. 汽车工程，2008,30(11)：964-968. Zhu Hangbin, Liu Xuejun. Effect of Frontal Crash Pulse on Occupant Injury Response[J]. Automotive Engineering, 2008，30(11):964-968.

[12] 胡宏勋，刘学军.车身正面结构碰撞性能开发方法[C]//中国汽车安全技术研讨会.重庆，2010：1-8.

[13] Jovan O，Simonetta B，Giovanni B. Lightweight Design and Crash Analysis of Composite Frontal Impact Energy Absorbing Structures[J]. Composite Structures，2012，94(2)：423-430.

(编辑 王艳丽)

Design Optimization of Key Structures in Frontal Crash Based on ESLMG

Chen Tao Dai Jianglu Chen Zikai Li Qiqi Li Zhuo

State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Changsha,410082

In inheritance development processes of existing vehicle models, it was difficult to optimize and redesign the structures efficiently and accurately because of the limitations of structure sizes and general arrangements. A procedure which contained withG1-G2design regulation, crash load path and an ESLMG was proposed to overcome the disadvantages to improve the performance of key structures in frontal crash. First, the equivalent double step target curve was defined, which was satisfied for the requirements of passenger injury according toG1-G2regulation and crash loads database was built by collecting and analyzing competing models. Then, frontal crash key structures of original model were determined as optimization objects and the thicknesses of them were optimized using ESLMG after optimizing their shapes. Finally, the optimized structures were input into full vehicle model to verify if its acceleration curve had achieved the optimization target or not. The validity of this procedure was proved with the calculation results of numerical examples.

structure nonlinear dynamic optimization; equivalent static loads method based on gradient(ESLMG);G1-G2design regulation; crash load path; vehicle body platform

2016-02-02

国家国际科技合作计划资助项目(2014DFG71590-101);广西科学研究与技术开发计划资助项目(桂科合14125008-2-25);国家自然科学基金资助项目(61540031)

U463.82

10.3969/j.issn.1004-132X.2016.24.022

陈 涛，男，1978年生。湖南大学汽车车身先进设计制造国家重点实验室助理研究员、博士。主要研究方向为汽车碰撞安全、汽车CAE技术、覆盖件冲压仿真与冲压工艺设计、计算可视化等。发表论文20余篇。戴江璐，女，1990年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。陈自凯，男，1988年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。李奇奇，男，1990年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。 李 卓，男，1988年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。