局部特征尺度分解结合局部均值解调的齿轮故障诊断

崔伟成 许爱强 李 伟 孟凡磊

海军航空工程学院，烟台，264001

局部特征尺度分解结合局部均值解调的齿轮故障诊断

崔伟成 许爱强 李 伟 孟凡磊

海军航空工程学院，烟台，264001

为了准确地进行故障诊断，根据齿轮故障振动信号的多分量调幅-调频特征，提出了一种新的解调方法——局部均值解调法，将之与局部特征尺度分解相结合进行齿轮故障诊断。该诊断方法首先对齿轮振动信号运用局部特征尺度分解，得到若干个内禀尺度分量，然后应用局部均值解调法求取每个分量的调频分量，最后根据瞬时频率的频谱进行故障诊断。采用仿真信号将局部均值解调法与Hilbert解调法、经验调幅调频分解法进行了对比，结果表明，局部均值解调法的精确性更好。通过齿轮故障振动数据的分析，验证了局部特征尺度分解结合局部均值解调的故障诊断方法的有效性。

局部特征尺度分解；局部均值解调；瞬时频率谱；齿轮故障诊断

0 引言

齿轮传动是一种常见的运动和动力传递方式，广泛地应用于机械设备中。齿轮故障会导致机械设备的整体性能下降，甚至引起严重设备事故从而造成重大经济损失[1-2]，因此，研究齿轮故障诊断方法具有实际意义。而齿轮的振动信号蕴含了齿轮的运行状态信息，所以，通常通过振动信号分析进行齿轮故障诊断。

齿轮故障的振动信号一般具有非线性、非平稳的特性，为了准确地将信号分解，进而得到分量的局部特征，许多学者开展了时频分析技术的研究[3-5]。其中，经验模态分解(empirical mode decomposition，EMD)是一个研究的热点。作为一种有效的自适应时频分析方法，EMD与Hilbert变换(Hilbert transform, HT)相结合，被广泛地应用于齿轮故障诊断领域[6-8]。但EMD在使用过程中存在一些问题，如过包络、欠包络、端点效应、模态混叠等[6-8]。因此，国内外学者一直在寻求EMD的改进、替代方法。

程军圣等[9]在本征时间尺度分解(intrinsic time-scale decomposition, ITD)[10]的基础上创造性地提出了局部特征尺度分解(local characteristic-scale decomposition，LCD)方法，该方法在保证分解所得分量物理意义清晰的基础上，具有计算时间短、端点效应不明显等优势，开拓了自适应时频分析方法的新思路[11-12]。

齿轮故障振动信号可以看成多个调幅-调频信号的叠加，通过LCD可将信号分解成单个调幅-调频分量之和，对每个分量进行解调再进行故障诊断是一种有效的方法。常用的解调方法有Hilbert解调和经验调幅调频分解(empirical AM-FM decomposition, EAD)。Hilbert法的不足是：包络本身光滑性较差，且端点效应明显，求取信号瞬时频率时会出现负频率现象[13]。EAD法可避免Hilbert变换引起的端点效应及负频率，但EAD法只是一种经验方法，缺乏严密的理论推导[14]。因此，研究新的解调方法具有一定的工程意义。

为了准确分析齿轮故障振动信号蕴含的故障特征，本文提出了一种新的解调方法——局部均值解调法，并结合LCD进行故障诊断。

1 基本理论

1.1 LCD方法

LCD方法将一个信号x(t)分解成若干个内禀尺度分量(intrinsic scale components，ISC)之和[10-12]。每个ISC分量必须满足2个条件：①任意2个相邻的极值点符号互异；②考虑所有的极值点Xk及对应的时刻τk(k=1，2，…，M，其中M为极值点的个数)。

取两个相距最近且符号互异的极值点(τk,Xk)和(τk+2,Xk+2)，按照下式定义一个τk+1时刻的函数值：

(1)

则Ak+1与极值点Xk+1的比值关系不变，即

αAk+1+(1-α)Xk+1=0

(2)

式中，α∈(0,1)为一常量，典型地，α=0.5。

为了筛选出ISC分量，LCD方法构造了信号的均值曲线，将均值曲线不断地从原信号中分离，其迭代过程与EMD方法类似，不同之处在于均值曲线的构造方法。LCD方法用均值点构造均值曲线，均值点的定义为

Lk+1=αAk+1+(1-α)Xk+1

(3)

式中，Lk+1为均值点，在迭代结束时数值为0。

标准LCD算法采用分段线性方法由均值点Lk计算均值曲线。为了得到更光滑的ISC分量，本文采用三次样条方法替代分段线性方法。

1.2 局部均值解调法

文献[14]提出了EAD法，指出该方法大多数情况下较Hilbert法有优势，笔者通过理论分析及数值仿真发现，在ISC分量的解调中，有必要对EAD法进行改进。

EAD法的基本思路是：将信号的所有极值点取绝对值，用三次样条函数插值形成包络函数，用原始信号除以包络函数得到标准化信号；若标准化信号为调频分量，则分解结束，否则将标准化信号作为原始信号，重复分解过程。通常情况下，迭代2～3次，标准化分解就会结束，信号可以表示为调幅分量(包络)和调频分量的乘积。

在上述过程中，有两点需要注意：

(1)EAD法认为信号是零均值对称的，所以将所有极值点取绝对值，进而求包络函数。但在实际应用中，LCD分解得到的分量往往不能满足EAD法的假设，只能“局部”满足“零均值对称”，这一点从均值点的定义及均值曲线的构造过程可以看出。为了从数值上说明这个问题，图1给出了调幅-调频信号x(t)的均值曲线。x(t)为

x(t)=0.3(1+0.5 sin5πt)sin(120πt+20πt2)

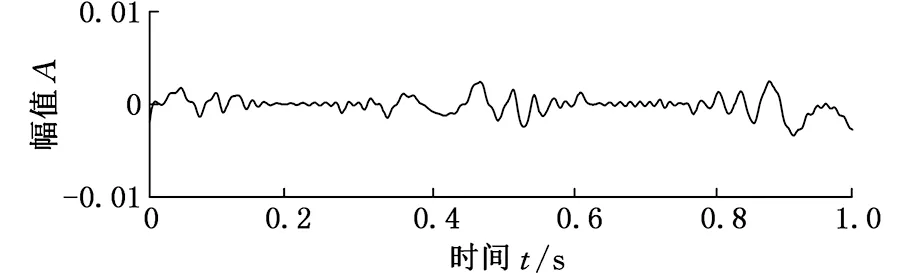
图1 调幅调频信号的均值曲线

由图1可以看出，LCD方法定义的均值曲线是零均值的近似，在局部范围内与零值存在较大的偏差，按照均值曲线迭代得到的ISC分量并非是零均值对称的，而EAD法按照全局零均值处理求包络理论上存在误差，利用局部信息则能减小其影响。因此，在构造包络函数时，考虑用“局部均值曲线”代替“全局均值曲线”。

(2)EAD法采用三次样条插值方法求包络函数，存在“过包络”、“欠包络”的问题，从而导致解调精度下降。为了避免这种情况，考虑用滑动平均法代替三次样条插值。

基于以上两点考虑，参考局域均值分解(local mean decomposition，LMD)[15]的思想，提出了一种局部均值解调(local mean envelope，LME)法，将信号的调幅部分和调频部分分离。与EAD法相比，该方法在包络函数的构造方法上作了改进，其余步骤相同。包络函数的构造方法为：计算信号的局部均值点，采用滑动平均法求局部均值曲线，用原信号减去局部均值曲线，得到零均值对称曲线，用滑动平均法计算包络函数。计算过程如下。

(1)确定第j个ISC分量ISCj(t)的所有局部极值点ni及其时刻tni，计算均值点mi、局部幅值ai：

(4)

(5)

(2)用滑动平均法得到均值函数m11(t)、包络估计函数a11(t)。

(3)将局部均值函数m11(t)从原始信号ISCj(t)中分离出来，得到

h11(t)=ISCj(t)-m11(t)

(6)

(4)用h11(t)除以包络估计函数对h11(t)进行解调，得到

s11(t)=h11(t)/a11(t)

(7)

(5)重复步骤(1)～(4)k次，直至得到一个纯调频信号s1k(t)(瞬时幅值均小于1)及k个包络信号a1k(t)，按照下式计算包络信号：

(8)

从LME解调法的流程可以看出，其实质就是将一个ISC分量视为一个乘积函数(product function，PF)分量和一个剩余信号之和，然后按LMD方法迭代的第一步求出一个纯调频信号和一个包络信号，剩余信号视为计算误差舍去。ISC分量与PF分量的定义内涵类似，剩余信号很小，可作为误差舍去。

1.3 瞬时频率计算

对纯调频信号s1k(t)利用反正切函数计算相位：

(9)

将φ(t)展开并求导，可得到瞬时频率。

求导计算会导致局部极值点附近的瞬时频率出现畸点，可对瞬时频率作平滑或滤波处理。本文采用滑动平均法，对任何一个瞬时频率的计算结果取连续3个采样点的平均值。

1.4 基于瞬时频率频谱的齿轮故障诊断

当齿轮存在故障时，其振动信号会出现调幅、调频现象。忽略传递函数的影响，齿轮故障振动信号可表示为[8]：

(10)

am(t)=Xm(1+dm(t))

(11)

Φm(t)=2πmzfrt+φm+bm(t)

(12)

式中，fr为轴的转频；z为齿轮的齿数；Xm为第m阶啮合频率谐波分量的幅值；φm为第m阶啮合频率谐波分量的初相位；dm和bm(t)为第m阶啮合频率谐波分量的幅值和相位调制函数，两者都是以fr及其倍频为重复频率的周期函数。

根据瞬时频率fm(t)的定义：

(13)

可以看出fm(t)可反映bm(t)的信息。

应用LCD方法对y(t)进行分解，对ISC分量求出瞬时频率fm(t)。fm(t)是一个以齿轮转轴转频及其倍频为中心的频率分量。对fm(t)进行频谱分析进而得到瞬时频率谱，由瞬时频率谱可以直观地判断fr及其倍频是否存在，从而进行故障诊断。

2 仿真数据分析

考察下式所示的仿真信号：

(14)

其中，x(t)为仿真信号，由调幅调频信号x1(t)、正弦信号x2(t)合成；采样频率为fs=1024 Hz，仿真时间t∈[0,1]。对仿真信号进行LCD，得到2个ISC分量和一个剩余信号r(t)，仿真信号及分解结果见图2。

图2 仿真信号及LCD分解结果

由图2可以看出，LCD能将调频调幅信号、正弦信号分解出来，剩余信号幅值很小，具有良好的分解能力。

为了比较Hilbert法、EAD法和LME法的效果，分别采用三种方法对两个ISC分量进行包络解调，将瞬时幅值直接给出。对EAD法和LME法采用反正切法计算瞬时频率，三种方法的瞬时频率计算结果均采用三点平滑处理。

图3、图4所示是两个ISC分量瞬时幅值的计算结果，可以看出三种方法解调结果均能反映原始信号的变化趋势，其中，Hilbert法计算结果波动最大且端点处的计算值严重偏离理论值；EAD法效果优于Hilbert法；LME法求得的瞬时幅值最贴近理论值，端点效应最小，更符合原始信号的实际特征。

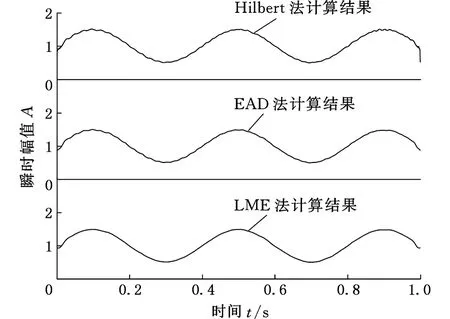
图3 第1个ISC分量ISC1(t)的瞬时幅值

图4 第2个ISC分量ISC2(t)的瞬时幅值

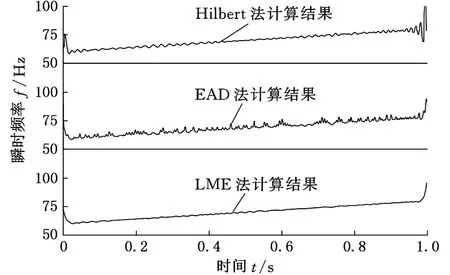
图5 第1个ISC分量ISC1(t)的瞬时频率

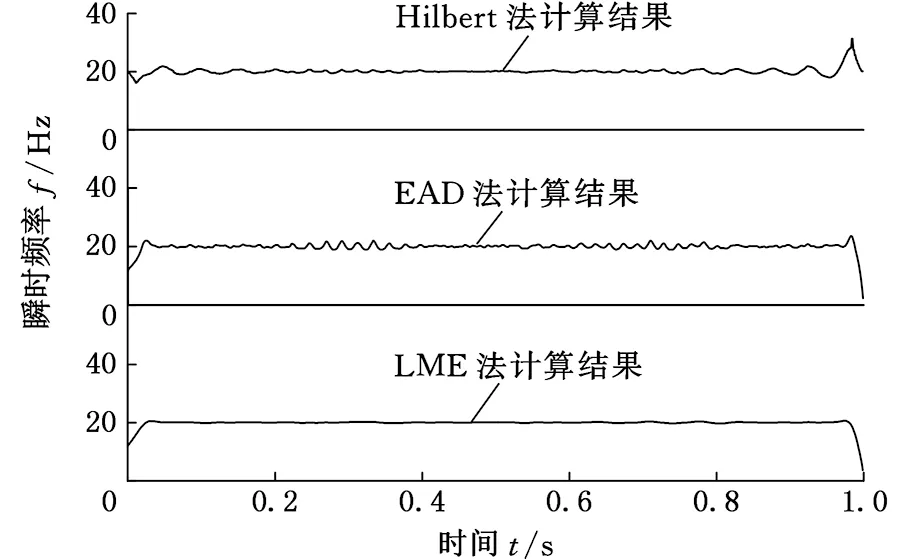
图6 第2个ISC分量ISC2(t)的瞬时频率

图5、图6所示是两个ISC分量瞬时频率的计算结果，可以看出不同方法计算结果差别较大：①在ISC1(t)的计算结果中，Hilbert法端点效应最明显，两端的计算误差已超过实际频率；EAD法的端点效应较Hilbert法有明显改善，但中间段的精确度有所下降；LME法计算结果最好；②在ISC2(t)的计算结果中，Hilbert法端点效应最小，EAD法端点效应最大；而中间段的计算效果，LME法最好，Hilbert法与EAD法相当。

总的来说，在瞬时幅值的计算方面，三种方法计算误差均不大，LME法优于EAD法，Hilbert法效果最差；在瞬时频率的计算方面，计算误差均较大，从端点和中间段的综合效果来看，LME法最优，Hilbert法最差。

3 试验数据分析

图7 齿轮箱传动结构

齿轮故障试验数据源于QPZZ-Ⅱ旋转机械振动分析及故障诊断试验平台系统，其齿轮箱传动结构如图7所示。变频调速电机通过联轴节驱动小齿轮，大齿轮与小齿轮直接啮合。大小齿轮均为圆柱齿轮，大齿轮齿数为75，小齿轮齿数为55。

人为地将小齿轮的一个齿尖切割约5 mm，模拟小齿轮断齿中度故障。试验中，大齿轮输出轴负载为零。设置电机轴转速为880 r/min，实测转速878 r/min，则小齿轮的转频f1=14.6 Hz，大齿轮的转频f2=10.7 Hz，齿轮啮合频率为804.8 Hz。采用加速度传感器采集振动信号，传感器在输出轴电机侧轴承处垂直于齿轮箱上表面安装，信号采样频率为fs=5120 Hz，计算数据点N=1024。

(a)时域波形

图8给出了原始信号的时域波形图及包络谱。从时域波形图上可以看出原始信号具有调幅-调频特性，并且存在周期性冲击。为了验证LCD本身的能力，本文没有采用中值滤波、SVD等降噪技术，包络谱直接采用Hilbert法求出，为了观察特征频段的特征，只给出了低频段(0～1000 Hz)的波形。从包络谱上可以看出20 Hz、45 Hz处有明显谱峰。20 Hz可近似认为是大齿轮转频的2倍频，45 Hz可近似认为是小齿轮转频的3倍频，由此可以判定齿轮箱出现了故障，但不能判定哪个齿轮出现了故障。

(b)包络谱

对原始采样信号进行LCD，得到4个ISC分量和1个剩余信号。图9是4个ISC分量的时域波形。可以看出：①LCD类似于自适应滤波器，4个ISC分量所包含的频率段逐渐降低；②每个ISC分量的幅值依次减小；③每个ISC分量均可近似认为是调幅-调频分量。因此，LCD是一种有效的信号自适应分解方法。

图9 原始信号LCD的ISC分量时域波形

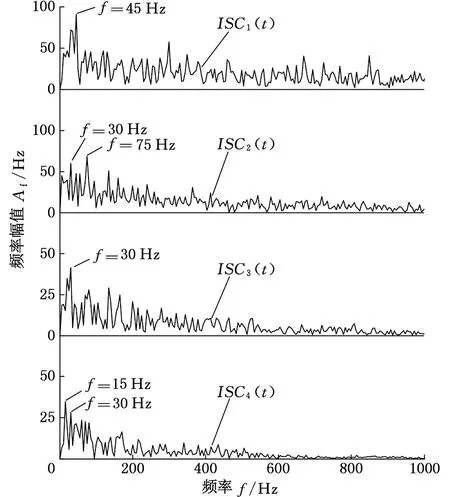
图10 应用Hilbert法解调的ISC分量瞬时频率谱

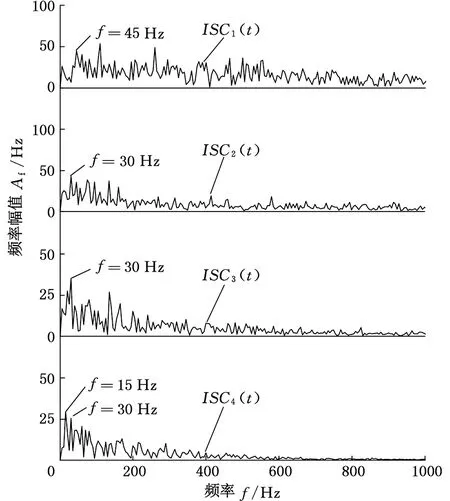
图11 应用EAD法解调的ISC分量瞬时频率谱

图12 应用LME法解调的ISC分量瞬时频率谱

对4个ISC分量分别应用三种方法解调，并求瞬时频率谱，将低频段(0～1000 Hz)的结果列于图10～图12。可以看出：①在分量1的瞬时频率谱中，小齿轮转频3倍频处存在相对明显的谱线；②在分量2、3的瞬时频率谱中，小齿轮转频2倍频处存在相对明显的谱线；③分量4的瞬时频率谱能清晰反映小齿轮转频及其2倍频。因此， LCD结合三种解调方法求出的瞬时频率谱均能得出小齿轮存在故障的正确结论。

但是Hilbert法求得的瞬时频率谱中存在明显的高频能量泄漏现象，其他频段的谱线杂乱，干扰较大；在EAD法求得的瞬时频率谱中，高频段的干扰得到明显的抑制；而LME法求得的瞬时频率谱高频干扰最小，信噪比最高。因此，LME法在齿轮故障诊断中具有一定的优越性。

4 结论

本文根据齿轮故障振动信号的多分量调幅-调频特征，提出了局部特征尺度分解(LCD)和局部均值解调(LME)相结合的故障诊断方法。通过仿真信号验证了LME解调的精确性；通过齿轮断齿故障振动数据的分析，验证了LCD结合LME的故障诊断方法的有效性，该方法不仅能够诊断出齿轮箱故障与否，还能准确地定位发生故障的齿轮，具有一定的工程应用价值。

[1] 康海英, 祁彦洁, 阎文, 等. 运用阶次跟踪和奇异谱降噪诊断齿轮早期故障[J]. 振动测试与诊断, 2010,30(6):662-665. Kang Haiying, Qi Yanjie, Yan Wen, et al. Early Fault Diagnosis and Singular of Gear Spectrum by Order Tracking Denoising[J]. Journal of Vibration Measurement & Diagnosis, 2010,30(6): 662-665.

[2] 赵军, 崔颖, 赖欣欢, 等. 随机共振降噪下的齿轮微弱故障特征提取[J]. 中国机械工程, 2014, 25(4): 539-546. Zhao Jun, Cui Ying, Lai Xinhuan, et al. Weak Texture Extraction of Gear Faults Based on Stochastic Resonance Denoising[J]. China Mechanical Engineering, 2014, 25(4): 539-546.

[3] Huang N E, Shen Z, Long R S, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proc. Roy. Soc. London, 1998, 454: 903-995.

[4] Huang N E, Shen Z, Long S R. A New View of Nonlinear Water Waves: the Hilbert Spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417-457.

[5] Huang N E, Chiang W, Busalacchi A J. A Bridge Health Monitoring Method Using the Hilbert-Huang Transform: a Case Study [R]. Washington: Nasa, 2000.

[6] Huang N E，Wu Z H. A Review on Hilbert-Huang Transform: Method and Its Applications to Geophysical Studies[J]. Adv. Adapt. Data Anal., 2009, 1: 1-23.

[7] 于德介, 程军圣, 杨宇. 机械故障诊断的Hilbert-Huang变换方法[M]. 北京: 科学出版社. 2006.

[8] 于德介, 程军圣, 杨宇. Hilbert-Huang变换在齿轮故障诊断中的应用[J]. 机械工程学报, 2005, 41(6): 102-107. Yi Dejie, Cheng Junsheng, Yang Yu. Application of Hilbert-Huang Transform Method to Gear Fault Diagnosis[J]. Chinese Journal of Mechanical Engineering，2005，41(6)：102-107.

[9] 程军圣, 郑近德, 杨宇. 一种新的非平稳信号分析方法—局部特征尺度分解法[J]. 振动工程学报, 2012, 25(2): 215-220. Cheng Junsheng，Zheng Jinde，Yang Yu. A New Non-Stationary Signal Analysis Approach—The Local Characteristic-Scale Decomposition Method[J]. Journal of Vibration Engineering，2012，25(2)：215-220.

[10] Frei M G，Osorio I. Intrinsic Time-scale Decomposition: Time-frequency-energy Analysis and Real-Time Filtering of Non-stationary Signals[J]. Proc. Royal Soc. A, 2007, 463: 321-342.

[11] 杨宇, 曾鸣, 程军圣. 局部特征尺度分解方法及其分解能力研究[J]. 振动工程学报, 2012, 25(5): 602 -609. Yang Yu, Zeng Ming, Cheng Junsheng. Research on Local Characteristic-scale Decomposition and Its Capacities[J].Journal of Vibration Engineering，2012，25(2)：602-609.

[12] 杨宇, 曾鸣, 程军圣. 局部均值尺度分解方法及其分量判据研究[J]. 中国机械工程, 2013, 24(2): 195-208. Yang Yu, Zeng Ming, Cheng Junsheng. Research on Local Characteristic-scale Decomposition and Its Stopping Criteria[J]. China Mechanical Engineering, 2013, 24(2): 195-208.

[13] 戴豪民, 许爱强. 瞬时频率计算方法的比较研究和改进[J]. 四川大学学报(自然科学版), 2014, 51 (6): 1197-1203. Dai Haomin, Xu Aiqiang. Comparative Research and Improvement on the Calculation Method of Instantaneous Frequency[J]. Journal of Sichuan University(Natural Science Edition), 2014,51(6):1197-1203.

[14] Huang N E. Computing Instantaneous Frequency by Normalizing Hilbert Transform: U.S., 6901353[P]. 2005-05-31.

[15] Smith J S. The Local Mean Decomposition and Its Application to EEG Perception Data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.

(编辑 苏卫国)

Gear Fault Diagnosis Based on LCD and LME Demodulation Approach

Cui Weicheng Xu Aiqiang Li Wei Meng Fanlei

Naval Aeronautical and Astronautical University,Yantai，Shandong,264001

In order to diagnose the gear fault accurately, according to the amplitude-modulated and frequency-modulated characteristics of the gear fault vibration signals a modle was proposed based on LCD and LME. Firstly，the original vibration signals were disposed by LCD．Secondly, the intrinsic mode components of LCD were envelope demodulated by LME. Finally, the gear faults were diagnosed by the instantaneous frequency spectrum. The analysis of the simulated data shows that the LME mode may get more accurate results of instantaneous amplitude and instantaneous frequency than that of Hilbert mode and empirical AM-FM decomposition mode. The analysis of gear fault data shows that the method based on LCD and LME may realize the fault diagnosis effectively.

local characteristic-scale decomposition(LCD); local mean envelope(LME) demodulation; instantaneous frequency spectrum; gear fault diagnosis

2015-12-18

国家部委预研基金资助项目(9140A27020214JB1446)

TN911.23；TP206.3

10.3969/j.issn.1004-132X.2016.24.012

崔伟成，男，1981年生。海军航空工程学院飞行器工程系讲师、博士研究生。研究方向为装备智能故障诊断。发表论文13篇。许爱强，男，1963年生。海军航空工程学院飞行器检测与应用研究所教授。李 伟，男，1980年生。海军航空工程学院飞行器工程系讲师。孟凡磊，男，1978年生。海军航空工程学院飞行器工程系讲师。