功率分流式混合动力系统发动机起动平顺性控制研究*
2017-01-09程辉军朱建新张彤王晨
程辉军朱建新张彤王晨
(1.上海交通大学,上海 200240;2.科力远混合动力技术有限公司,上海 201501)
功率分流式混合动力系统发动机起动平顺性控制研究*
程辉军1,2朱建新1,2张彤2王晨2
(1.上海交通大学,上海 200240;2.科力远混合动力技术有限公司,上海 201501)
为改善功率分流式混合动力系统纯电动至混合动力模式切换性能设计了一套控制算法。通过发动机曲轴位置和拖转扭矩预估行星架输入端的阻力,在转矩分配时将该扭矩作为输入条件,从而消除因发动机拖转扭矩波动导致的整车抖动;根据整车动力学模型设计状态观测器,以输出轴转速和轮边转速之差为反馈进行闭环控制,以减少输出轴转速波动。通过模型仿真和实车试验对该控制算法的有效性进行验证。
1 前言
搭载行星排耦合技术的功率分流系统的深度混合动力汽车不仅燃油利用率高、节能减排效果好,而且市场占有率高,已成为未来混合动力汽车的发展趋势。在混合动力系统中,为了降低油耗和排放,汽车行驶过程中发动机的起停非常频繁,因此提高发动机起动过程中整车的平顺性变得尤为重要[1]。因功率分流式混合动力系统结构的原因,发动机、电机和驱动轮始终耦合在一起,任何一轴的扭矩波动都会影响到最终的扭矩输出[2~3]。在起动和熄火过程中,由于发动机端扭矩会产生突变,导致整车在起动、熄火工况下抖动明显,严重影响了车辆的平顺性和驾驶感受。为了提升驾驶性能,需要研究一套针对此类问题的控制策略。
2 混合动力系统结构原理及发动机起动过程介绍
2.1 结构原理
功率分流式混合动力系统是指采用动力分离装置将来自发动机的能量进行合理分配,平衡发动机负荷,并形成多种动力传递模式的混联式混合动力系统。目前功率分流系统一般采用具有多自由度、输入输出灵活可控、结构紧凑、体积小、速比大等优点的行星排结构,其典型结构有丰田单模和通用双模为代表的功率分流深度混合动力系统。
所研究的功率分流式混合动力系统是一款双行星排单模混合动力系统,如图1所示。可知,行星架PC通过扭转减振器与发动机相连,前行星排的太阳轮S1与电机MG1相连,后行星排的太阳轮S2与电机MG2相连,前行星排外齿圈R1通过主减速器和差速器的连接将动力输出到驱动轮上。另外,在箱体内部设计了两个湿式制动器B1和B2,必要时可以在系统工作过程中闭合其中一个来提高系统工作效率[4]。
该系统共有4种基本运行模式。在纯电动模式下,通过制动器锁止与发动机相连的行星架,由大小电机驱动整车实现纯电动行驶;在车辆静止状态下,可以原地起动发动机实现怠速发电;在急加速时,两个电机和发动机共同驱动行驶,满足大扭矩需求;在中高速行驶时,通过离合器锁止小电机,实现定速比驱动,降低中高速油耗[5]。
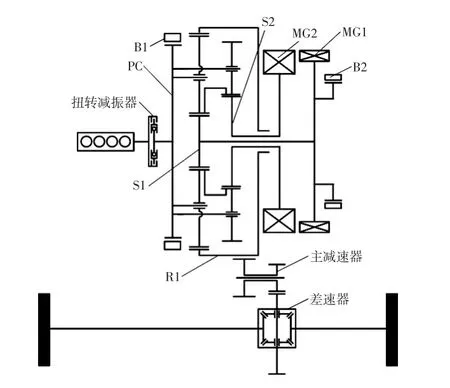
图1 双行星排单模混合动力系统结构简图
2.2 发动机起动过程
该系统的发动机起动过程与传统的起动方式不同,在静止或行驶过程中,整车控制器(HCU)根据当前剩余电量(SOC)、电池允许充放电功率、车速及加速踏板等信号判断起动条件。当整车控制认为需要起动发动机时,控制电机MG1将发动机以设定的扭矩曲线拖转到满足点火的转速,同时协调发动机完成起动过程,发动机起动完成后立即进入扭矩模式。在整个起动过程中,发动机倒拖到点火过程的扭矩冲击将被完全传递到输出轴上,处理不当将引起扭矩波动。加入控制算法前的波动数据如图2所示。

图2 加入控制算法前发动机起动过程抖动数据
可以看出,车辆抖动由两部分组成,刚开始拖转发动机时,由于发动机倒拖阻力会随着曲轴位置和转速发生变化,经过扭转减振器过滤后传递到行星架输入轴上;另一部分则发生在发动机点火瞬间,由于发动机从负扭矩到正扭矩发生跳变,也将扭矩波动传递过来,整车出现耸车现象。
3 数学模型的建立
3.1 发动机点火前控制算法
通过动力学原理和系统结构特性,可以将混合动力系统简化成图3所示的数学模型,其中Je为发动机转动惯量,Jst为行星架转动惯量,Js1为电机1转动惯量,Js2为电机2转动惯量,Jbd为整车等效到输出轴转动惯量,Jti为轮胎转动惯量,Jrg为差速器总成转动惯量,Kd为扭转减振器弹簧刚度,Cd为扭转减振器等效阻尼。
根据传动系统模型及动力学原理可得:
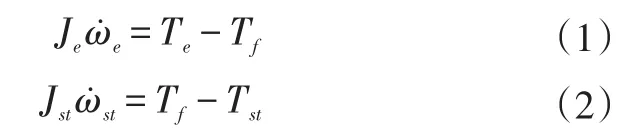
式中,Tf为扭转减振器两端受到的弹簧力;Te为发动机输出扭矩;Tst为行星架上输出扭矩;ωst为行星架角速度;ωe为发动机角速度;θst为行星架转过的角度;θe为发动机转过的角度。
同理,对行星齿轮分析可以得:

式中,ω˙e1、ω˙e2为电机MG1和MG2的角速度;Te1、Te2为电机MG1和MG2的输出扭矩;Tso1、Tso2为前、后行星排太阳轮上的输出扭矩;ω˙Ho为外齿圈的角速度;JHo为外齿圈的转动惯量;THL为轮边阻力等效到外齿圈的扭矩;THo为外齿圈的输出扭矩。
根据力矩平衡公式可以得到:

式中,io1为前行星排太阳轮到外齿圈的传动比;io2为后行星排太阳轮到外齿圈的传动比。
根据双行星排转速关系可得:

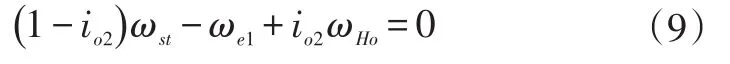
根据式(1)~式(9)可以得出状态方程:
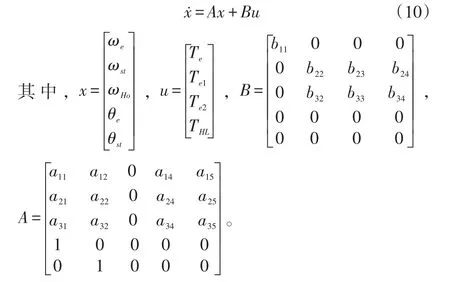
式中,aij、bij为与惯量和刚度阻尼相关的系数。
根据状态方程(10)可得:

式中,Ge(s)、Ge1(s)、Ge2(s)、GHL(s)分别是发动机、电机MG1、电机MG2和路面载荷作为输入,弹簧力为输出的传递函数。
为了方便计算,可以将发动机阻力Te分解成稳态分量Te_cont和动态ΔTe两部分组成。其中,Te_cont主要是受发动机转速和机油温度影响,ΔTe主要受发动机曲轴位置影响。把Tf分解成Tf_cont和ΔTf,同理将起动过程中的电机补偿扭矩分成Te1_cont和ΔTe1两个部分,Te2_cont和ΔTe2两个部分,因此式(11)式可以表示为:
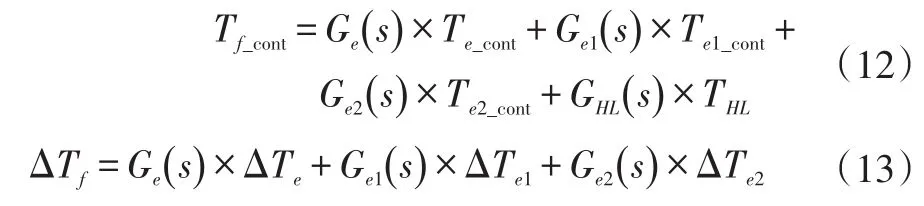
其中对式(12),可以设定已知THo、THL、ωst和Tf,根据式(3)~式(9)得到Te1_cont、Te2_cont。只要通过控制算法使ΔTf=0,发动机起动过程中的冲击将不再影响行星排的输入,从而降低整车抖动。
以ΔTf=0为目标,行星排扭矩输出THo保持不变,结合式(3)~式(9)和式(13)可以得到ΔTe1和ΔTe2。具体控制算法如图4所示。

图4 发动机补偿扭矩算法
发动机在点火成功前的扭矩τe_cont主要与发动机当前水温和转速相关,可以通过试验法结合理论估算得出近似值。Δτe与发动机曲轴转角和转速相关,可以通过理论计算结合试验法得到,如图5所示。
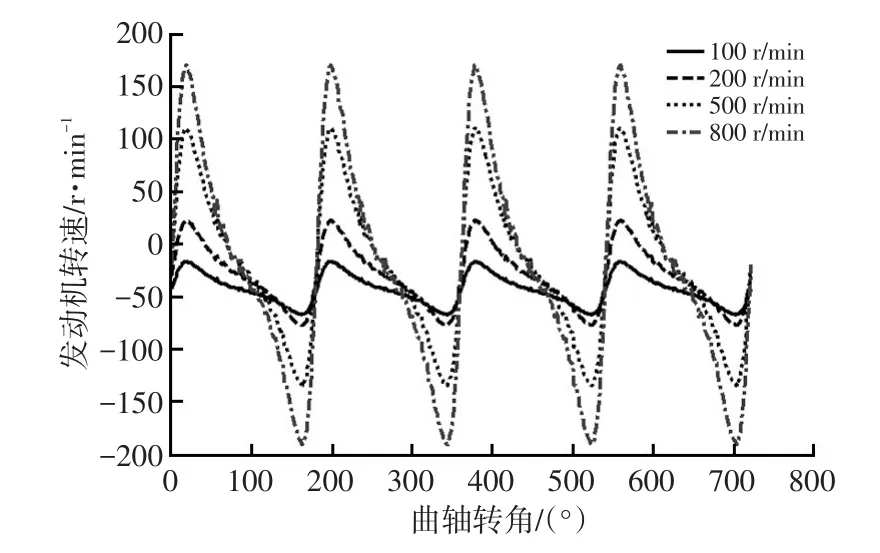
图5 发动机不同转速下的倒拖阻力矩曲线
3.2 发动机点火后控制算法
在发动机点火瞬间或输出扭矩发生改变时,整车会出现低频抖动,严重影响驾驶性。为了有效消除这种低频抖动,通过对输出轴后半部分进行分析,可以等效成图6所示系统。
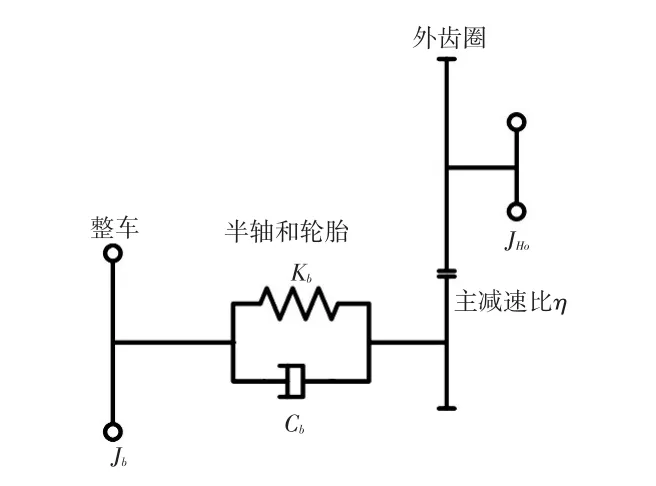
图6 轮边输出等效模型示意
根据轮边输出等效模型,可以得到以下方程:

式中,Jb为整车等效转动惯量;JHo传动系统的等效惯量;Cb为整车等效阻尼;Kb为整车等效刚度;ωHo为外齿圈转速;ωb为轮胎上的转速(等效到外齿圈);θHo为外齿圈转动角度;θb为轮胎转动角度(等效到外齿圈);THL为路面摩擦阻力,可以假设为恒定值,即T˙HL=0。
建立状态方程:

为了提高系统稳定性,将信号作为闭环调节,THo为:

其中,THo_ref是设定轮边驱动力,f是反馈系数。通过调节f值,可以使得系统的闭环极点落在实轴上并尽可能远离虚轴。
通常情况下可以通过图7的方式来确定需要配置的极点。系统在开环状态下有3个极点,其中一个落在原点,另外两个极点是一对共轭复根,当f增大时,其会逐渐接近实轴变成重根(图中b位置)。当f继续增大时,系统的两个极点往b点左侧移动,但是系统的响应速度将变慢。在本研究对象中,配置极点在b位置处,能够取得较好的效果。
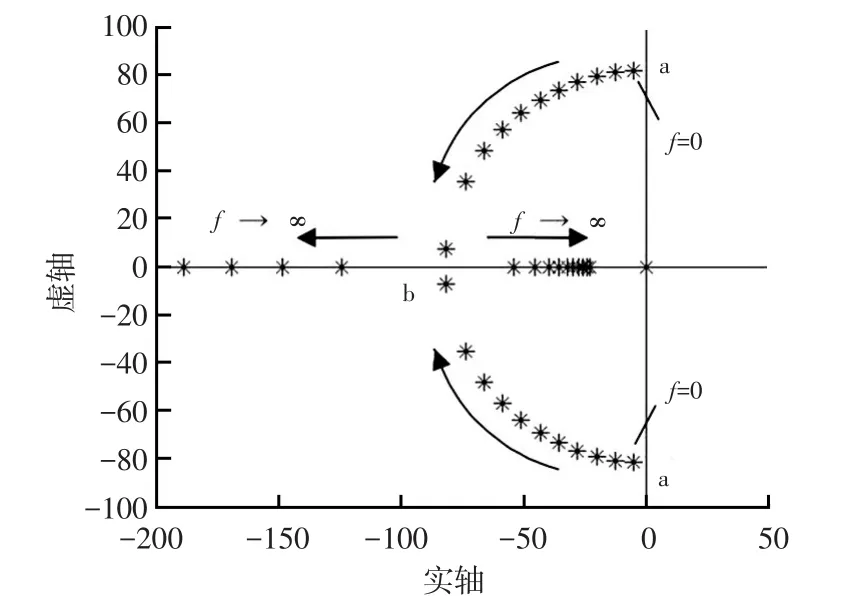
图7 根轨迹法计算反馈系数示意
实车运行过程中,方程中的ωHo可以直接通过电机测得,但是ωb很难直接测量,因此通过设计状态观察器的方式来观察出ωb。根据状态方程(16),输出ωHo作为反馈,设计状态观察器并将其离散化,具体如下:

式中,Fob为状态观察器反馈系数;是状态变量估计值;是观察出的轮边转速。
3.3 整体控制算法
结合以上两种算法的优点,在发动机点火之前采用传递函数估算输入扭矩的前馈算法,在发动机点火瞬间或其它扭矩突变时,采用反馈算法,两者之间根据状态切换,总体算法框图如图8所示。
4 仿真分析
为了更好地模拟实车中发动机的起动过程,在Matlab/Simscape下搭建整车传动系统的物理模型。根据数学模型在Matlab环境中编写m文件,求出、,再计算出当前扭转减振器弹簧力Tf。在Simulink下根据式(1)~式(9)求解出电机扭矩。使用Simulink建模验证控制算法,仿真结果如图9所示。可以看出,通过传递函数估算的弹簧力和实际弹簧力在发动机拖转过程中完全重合;在使用以上控制算法后,输出轴扭矩、加速度和转速波动得到显著改善。
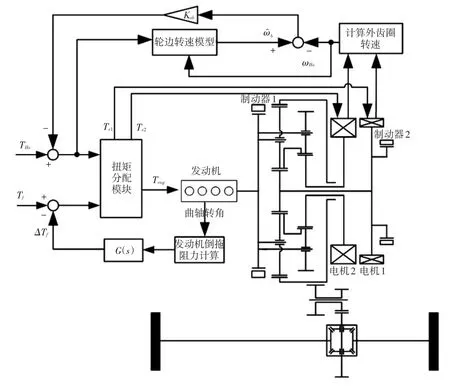
图8 整体控制算法

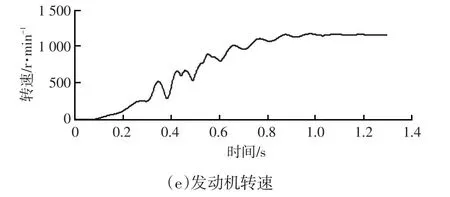
图9 仿真结果对比
5 实车验证
将控制算法在Matlab/Simulink中完成建模并通过模型在环(MIL)测试,使用dSPACE TargetLink软件在环(SIL)测试后,直接生成应用层C代码和a2l文件,将应用层代码和底层代码合并编译后生成格式为HEX和a2l的程序文件。通过INCA将HEX文件刷写到整车控制器中。在实车发动机起动过程中,主观的振动感受明显改善,通过座椅下加速度传感器测量结果(图10)可以明显看到两者的区别。
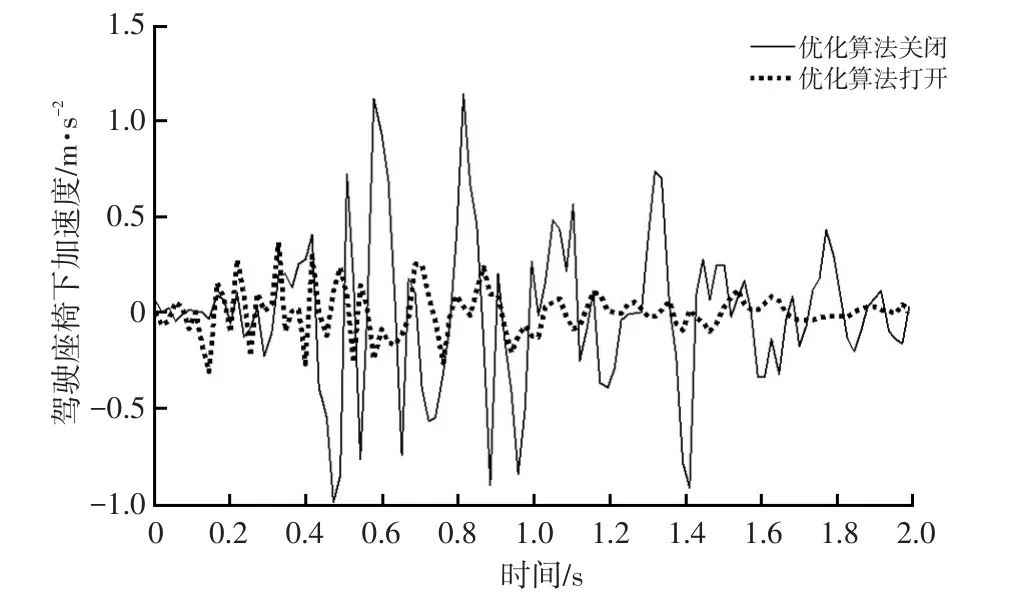
图10 加速度传感器测量结果对比
图11为起动电机叠加补偿力矩后的对比图,电机最大扭矩为±90 N·m,需求扭矩在电机能力范围之内。
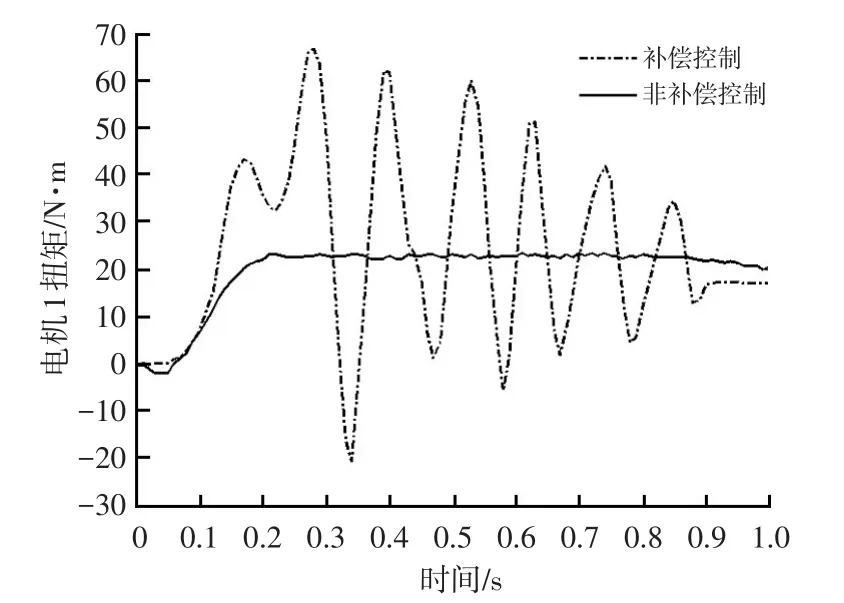
图11 补偿扭矩对比
1 Chen Jiashiun,Hwang Hsiuying.Engine automatic start–stop dynamic analysis and vibration reduction for a twomode hybrid vehicle.Journal of Automobile Engineering, 2013,227:1303.
2 Sugimura H,Takeda M,Takei M,et al.Development of HEV Engine Start-Shock Prediction Technique Combining Motor Generator System Control and Multi-Body Dynamics(MBD) Models.SAE Papper,2013-01-2007.
3 刘振军,赵江灵,秦大同,等.混合动力汽车纯电动工况起动发动机特性研究.重庆理工大学学报,2013,27(11):1~7.
4 于海生,张建武,张彤,等.电磁功率分流混合动力汽车传动控制模式研究.农业机械学报,2012,43(6):1~7.
5 张彤,余卫,马智涛,等.一种双行星排四轴传动装置.中国专利,102022489A.2011-3-30.
(责任编辑晨 曦)
修改稿收到日期为2016年5月1日。
Engine Start Control Study of Power-split Hybrid Electrical System
Cheng huijun1,2,Zhu Jianxin1,2,Zhang Tong2,Wang Chen2
(1.Shanghai Jiao Tong University,Shanghai 200240;2.Corun CHS Hybrid Technology Co.,Ltd.,Shanghai 201501)
In order to improve the switching performance from electric mode to hybrid mode in power-split hybrid system,a control algorithm was designed.Planetary carrier input end resistance was estimated according to engine crankshaft position and dragging torque,which was used as input condition in torque distribution,thus eliminating vehicle trembling caused by engine dragging torque fluctuation;according to vehicle dynamic model design state observer,the difference between output shaft speed and wheel speed was used as feedback for closed-loop control,thus to reduce output shaft speed fluctuation.Validity of this control algorithm was verified through model simulation and vehicle test.
Hybrid vehicle,Power-split,Engine,Start control
混合动力 功率分流 发动机 起动控制
U461.4
A
1000-3703(2016)12-0015-05
国家高技术研究发展计划项目(2011AA11A20)、国家自然科学基金(51275355)资助。
