页岩气基质纳米通道流动模拟研究
2017-01-07李俊南李世贵
李俊南 刘 洪 李世贵 李 倩
(1. 重庆科技学院石油与天然气工程学院, 重庆 401331;2. 中国石油西南油气田安全环保与技术监督研究院, 成都 610000)
页岩气基质纳米通道流动模拟研究
李俊南1刘 洪1李世贵1李 倩2
(1. 重庆科技学院石油与天然气工程学院, 重庆 401331;2. 中国石油西南油气田安全环保与技术监督研究院, 成都 610000)
结合活性炭表面扩散系数计算原理,建立页岩气在纳米孔道中的流动方程。模拟结果表明:通道半径为0~8 nm,通道中以吸附气的表面扩散为主,压力的影响可忽略不计;通道半径大于10 nm时,表面扩散通量相对较少,压力的影响不可忽略;当通道半径高于50 nm时,自由分子流动通量可以达到99%,压力是气体分子传输速度的主要影响因素。
等温吸附; 扩散系统; 表面扩散; 单相流动模型
具有极大开发潜力的页岩气藏属于非常规气藏的一种,该类气藏的天然气储集和运移均不同于常规气藏[1]。其中大部分气体主要吸附于基质中,仅有少量气体以自由气的形式存在于孔隙中。据统计,孔隙表面上甲烷的含量高达60%~70%,页岩气主要流动通道为纳米级通道[2]。目前国内外关于纳米级通道流动模型的研究较多。2009年,Javadpour建立了努森扩散、滑脱流动模型,提出了表观渗透率模型,初步揭示了页岩气在纳米级通道中的流动规律[3]。2015年,吴克柳结合郭亮测试的活性炭表面扩散系数测试方法提出了吸附气的表面扩散模型。但是,吴克柳所采用的活性炭表面扩散系数测试方法和活性炭的表面扩散系数计算原理有所不同,其页岩表面扩散模型存在不足之处,影响页岩气在纳米级孔道中流动模型的准确性[4-5]。
本次研究以纳维斯托克斯方程作为纳米级通道内自由分子的扩散理论基础,结合活性炭的表面扩散方程式,建立了页岩纳米级通道的物理扩散系统。在考虑游离气、吸附气的同时兼顾气体滑脱效应,应用该模型分析页岩气流动过程中自由气和吸附气的权重变化。
1 基质纳米通道流动模型建立
1.1 自由分子流动模型
页岩气的气体分子流动通道主要为纳米级通道。在此引用微分方程,将页岩气中自由气体分子在通道内的流动视为分子在微管中运动的理想状态。在该运动过程中,假设分子沿x、y、z方向运动,其流动状态如图1所示。
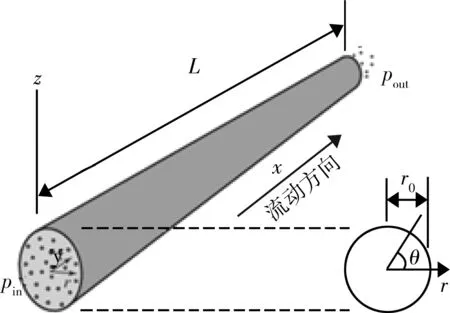
图1 自由气在通道中的流动示意图
根据N-S方程,建立x方向理想流体平面流动方程:
(1)
式中:u—— 气体分子的空间速度,ms;
p—— 压力,MPa;
ρ—— 页岩气密度,kgm3;
v——y方向的速度分量,ms;
μ—— 黏度,mPa·s;
gx——x方向重力加速度分量,ms2;
v′ ——x方向速度分量,ms。
按照毛管束处理法则,可将速度方程简化:
(2)
裂缝通道内的流动为轴对称,且在页岩基质中存在着解吸气的流动。假设解吸气在裂缝通道中的流动有效半径为rh,则式(2)可变换为式(3):
(3)
式中:r—— 毛管束半径,m;
L—— 毛管束长度,m;
Δp—— 压差,MPa。
再对微分方程的解进行积分,得到关于速度的方程:
(4)
在r=rh处,流体速度为0,由此得到参数c:
将c代入式(4),再进行积分:
(5)
式中:rh—— 解吸气在裂缝通道中流动的有效半径。
由流量公式计算得到:
(6)
求解式(6),得到气体扩散通量Jvs的关系式:
(7)
式中:Jvs—— 气体扩散通量,kg(m2·s);
M—— 气体摩尔质量,kgmol。
由于气体在喉道中流动时产生滑脱效应,因此引入Brown滑脱流动修正系数[7]:
(8)
式中:F—— 气体滑脱效应校正系数,无因次;
R—— 理想气体常数,(m3·Pa)(K·mol);
T—— 系统温度,K;
pavg—— 裂缝通道内平均压力,MPa;
α—— 孔隙壁面切向动量供给系数,无因次。
α的值与孔隙壁面形态,气体性质、温度、压力有关,通常为(0,1],取1时表示完全滑脱[8]。将式(7)代入式(8),得到修正后的气体扩散通量Jvs*关系式:
(9)式中:Jvs*—— 修正后的气体扩散通量,kg/(m2·s)。
1.2 解吸气表面扩散
由于页岩中含有大量的吸附气体,气体在孔隙渗流过程中存在吸附解吸现象,解吸气在页岩气的传输过程中具有重要作用。根据Langmuir等温吸附原理[9]:
(10)
式中:θ—— 气体有效解吸分子所占表面积与总吸附表面积之比;
b—— 吸附平衡常数;
kd—— 解吸平衡常数;
ka——吸附平衡常数。
吸附气在表面扩散的能量由化学势能梯度提供,类似于分子跳跃模型[10]。根据空间异相性,将表面扩散方向视为与化学势能梯度垂直的方向,其他方向不予考虑。在此只考虑化学势能降低的方向,此时平行于x轴向右运动的分子为分子总数的1/3。图2所示为表面扩散分子跳跃模型示意图。
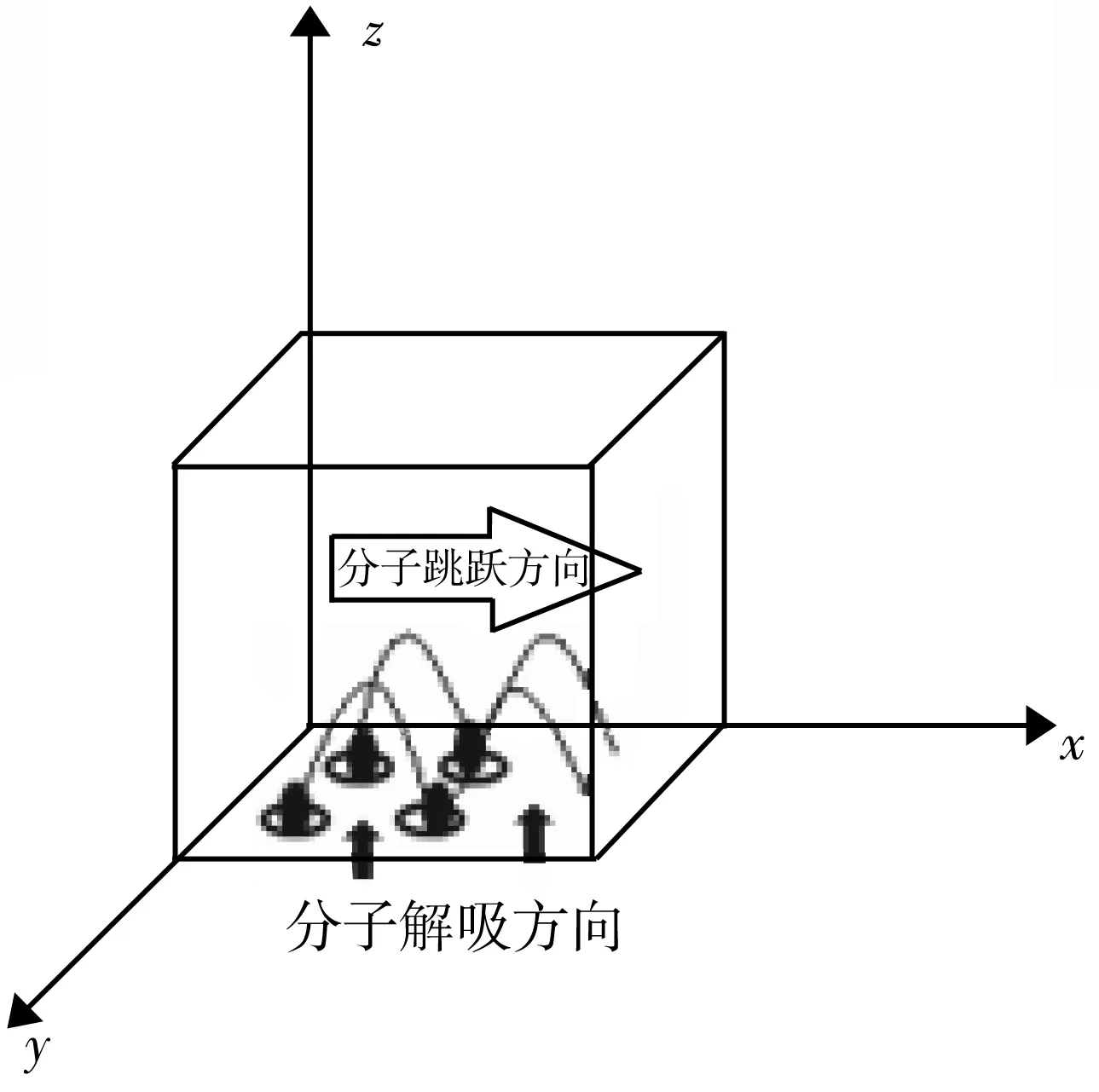
图2 表面扩散分子跳跃模型示意图
基于以上分析,得到Langmuir单层吸附气质量浓度的计算式:
(11)
式中:Cs—— 吸附气质量浓度,kg/m3;
NA—— 阿伏加德罗常数,mol-1;
r0—— 分子半径,m。
根据Maxstefan方法[11],表面扩散表达式定义为:
(12)
式中:Ds—— 表面扩散系数;
φ—— 孔隙度,%;
Cu—— 表面扩散的吸附气质量浓度,kgm3。
根据DO的结论[12],页岩表面扩散系数的计算公式为:
Ds=(kap+kd)Lμ/2
表面扩散的吸附气浓度为:
(13)
式中:pi—— 方程第i个点的压力,MPa;
pi+1—— 第i+1个点的压力,MPa。
将式(12)及表面扩散系数计算公式代入式(13),得到气体表面扩散通量Js表达式:

(14)
式中:Js—— 吸附气表面扩散通量,mol/(m2·s)。
1.3 流动模型建立
页岩气基质纳米通道中的流动主要由吸附气表面扩散和自由气滑脱流动所组成,在此建立页岩气纳米级通道流动物理扩散系统(见图3)。

图3 页岩气纳米通道物理扩散系统
分子有效流动半径表达式[12]为:
rh=r-dmθ
(15)
综上所述,页岩气通道内气体总传输量表达式为:
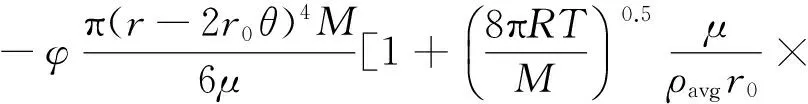
(16)
式中:JT—— 气体总传输量,mol/(m-1·s)。
根据达西定律,JT表达式可写成以下公式:
(17)
结合式(17)得到表观渗透率Kapp:

(18)
2 实例应用
2.1 常规参数选取
选取西南某区块页岩参数作为基础数据,总结得到模型参数表(见表1)。
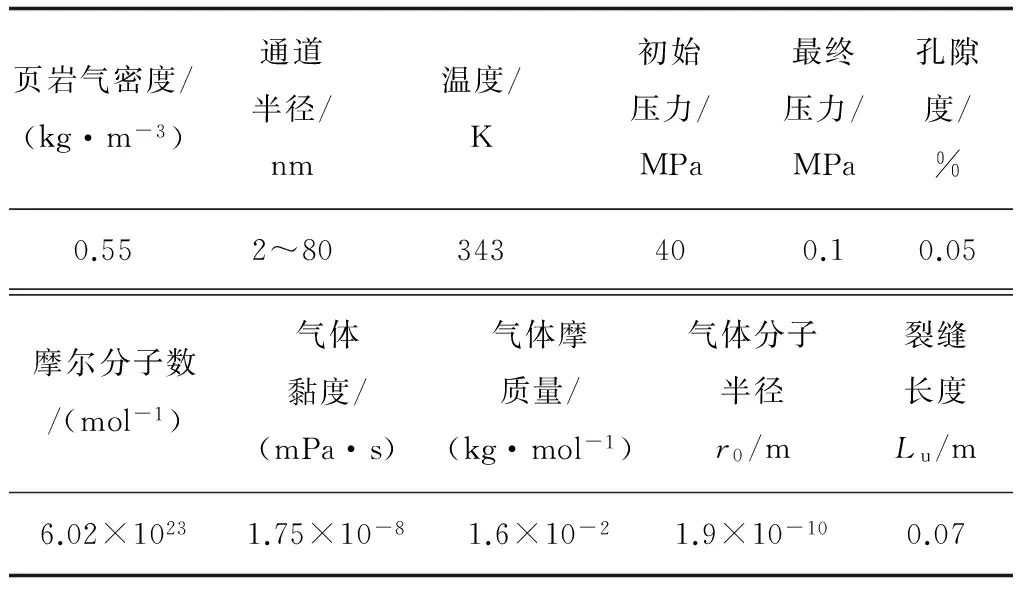
表1 模型参数表
2.2 解吸能力数据提取
以页岩气的实验解吸数据为准,通过温度压力校正公式得到符合地层温度70 ℃的实际Langmuire等温吸附曲线[13](见图4)。
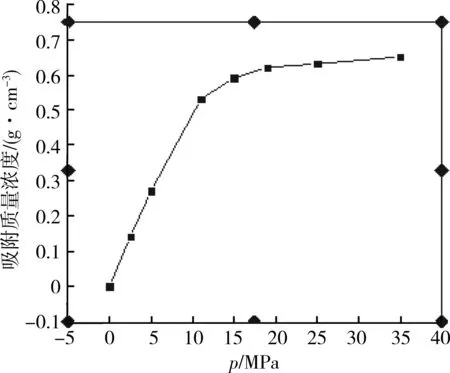
图4 页岩气等温吸附曲线
根据Langmuir等温曲线的数据对方程进行拟合,得到吸附能力b的值为0.16,无因次。图5所示为页岩气吸附能力拟合结果。
2.3 计算分析
传输流动通道半径不断增大时,随着压力的不断增加吸附气表面扩散所占的权重将先增大后减小。图6所示为流动通道对气体流动的影响。当流动通道半径为0~8 nm时,吸附气表面扩散通量所占比例较高,但随着流动通道变窄会逐渐降低。在该范围内,通道半径越小,吸附气表面扩散比例随压力增大而下降的速度越快,即分子解吸为自由滑脱流动分子的速度越快。

图5 页岩气吸附能力拟合结果

注:JT—— 含吸附气的总传输量;—— 不含吸附气的总传输量。
随着压力增大,气体表面扩散通量在减少,说明吸附气解吸能力的大小是影响表面扩散通量的重要因素。当地层压力保持在30 MPa以上时,吸附气几乎不会从页岩基质中解吸出来,表面扩散通量几乎为0;当压力在10 MPa以下且保持不变时,流动通道半径是影响表面扩散的重要因素;当通道半径大于10 nm以后,表面扩散通量相对较少,可忽略不计。图7所示为不同压力及通道半径下表面扩散通量变化曲线。
可以看出,气体自由分子流动通量主要受流动通道半径及压力的影响。当通道半径为0~8 nm时,自由分子流动所占比例几乎相同,压力的影响较小可忽略不计;通道半径为10~50 nm时,压力越高,自由分子流动分子所占比例越高,压力高于20 MPa时候,自由分子流动通量可以达到99%;当通道半径大于50 nm时,压力是气体分子传输速度的主要影响因素。图8所示为不同压力及通道半径下自由分子流动通量变化曲线。
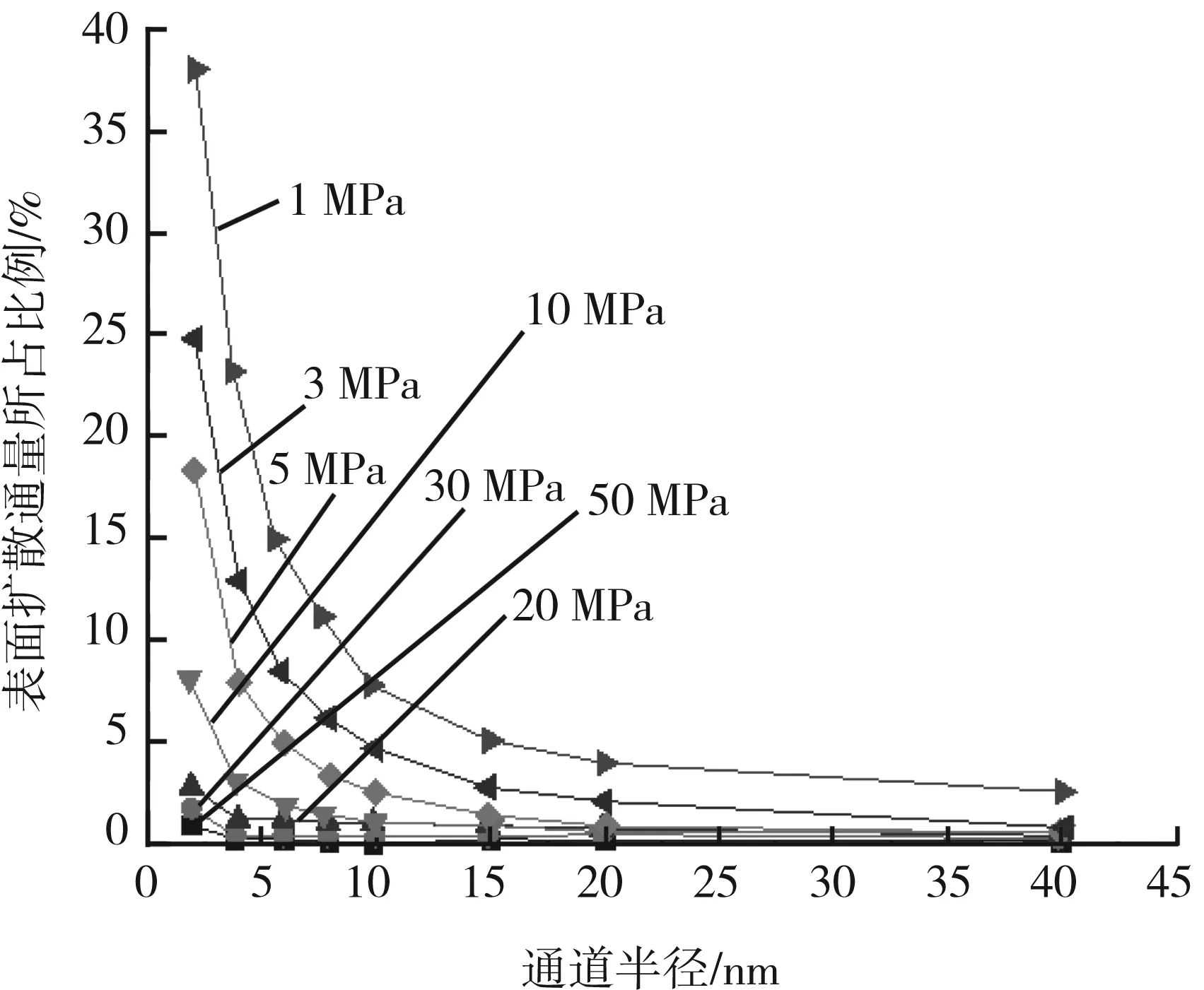
图7 不同压力及通道半径下表面扩散通量变化曲线

图8 不同压力及通道半径下自由分子流通量变化曲线
3 结 语
针对页岩气在纳米级流动通道的流动过程进行了综合分析。吸附气表面扩散、自由气体滑脱效应等均是页岩气在流动中的重要机制,其中表面扩散流动影响更为复杂。
在表面扩散的过程中,吸附质的表面扩散系数受吸附介质的影响较大,不同页岩的吸附能力会影响扩散系数的大小,而吸附能力只能通过页岩实验测得。在研究页岩气在纳米级通道流动规律时,必须针对岩心进行等温吸附实验测试。
随着流动半径增大,页岩气表面扩散的影响作用将减轻。当达到一定程度以后,气体分子滑脱黏性流动的权重最大,表面扩散通量极小或可以忽略不计。
[1] 魏明强,段永刚,方全堂,等.页岩气藏孔渗结构特征和渗流机理研究现状[J].油气藏评价与开发,2011,1(4):73-77.
[2] LU X C,LI F C,ATSON A T.Adsorbtion Measurements in Devonian Shales[J].Fuel,1995(4):74-81.
[3] JAVADPOUR F,FISHER D,UNSWORTH M.Nanopores and Apparentpermeability of Gas Flow in Mudrocks[J].Journal of Canadian Petroleum Technology,2009,48(8):16-21.
[4] 吴克柳,李相方,陈掌星.页岩气纳米孔气体传输模型[J].石油学报,2015,36(7):837-849.
[5] DO D D.Model for Surface Diffusion of Ethane and Propane in Active Carbon[J].Chemical Engineering Science,1996(51):297-310.
[6] BROWN G P,DINARD O A,CHENG G K,et al.The Flow of Gases in Pipes at Low Pressures[J].Journal of Applied Physics,1946,17(10):802-813.
[7] MILLIKAN R A.Coefficients of Slip in Gases and the Law of Reflection of Molecules From the Surfaces of Solids and Liquids[J].Physical Review,1923(1):17-238.
[8] 辜敏,陈昌国,鲜学福.Langmuir 方程在变压吸附过程中的应用[J].天然气化工,2002(1):29-32.
[9] CUNNINGHAM R E,WILLIAMS R J J.Diffusion in Gases and Porous Media[M].New York:Plenum Press,1980:51-59.
[10] 盛茂,李根生,黄中伟,等.考虑表面扩散作用的页岩气瞬态流动模型[J].石油学报,2014(2):347-353.
[11] DO D D,DO H D.Surface Diffusion of Hydrocarbons in Activated Carbon:Comparison Between Constant Molar Flow[J].Adsorption:Journal of The International Adsorption Society,2001(7):189-209.
[12] XIONG X,DEVEGOWDA D L,VILLAZON G G M,et al.A Fully-Coupled Free and Adsorptive Phase Transport Model for Shale Gas Reservoirs Including Non-Darcy Flow Effects[G].SPE 159758,2012:26-34.
[13] 王莉莎,陈乔,王森,等.页岩含气量的影响因素及预测[J].油气田地面工程,2014(2):42-45.
Research on Flow Simulation in Matrix Nano-Channel of Shale Gas
LIJunnan1LIUHong1LIShigui1LIQian2
(1. School of Petroleum and Natural Gas Engineering, Chongqing University of Science and Technology, Chongqing 401331, China; 2. Environmental Protection and Technical Supervision Institute,Southwest Oil and Gas Field Company, Chengdu 610000, China)
This paper combines the activated carbon surface diffusion coefficient calculation principle with shale isothermal adsorption experiment to establish the shale gas diffusion model. Simulation tests show that when the radius of channel in 0 ~ 8 nm range, there exists mainly the surface diffusion of the adsorbed gas, and the influence of pressure can be ignored; when channel radius is wider than 10 nm, surface diffusion is relatively small, and pressure should not be neglected; when the channel is further than 50 nm, free molecular flow flux can reach 99%, so the pressure is the most influencing factors of gas molecules.
isothermal adsorption; diffusion system; surface diffusion; single phase flow model
2016-03-29
国家自然科学基金项目“页岩气藏多重介质渗流机理与理论研究”(51374265);重庆科技学院研究生科技创新计划项目“威远区块水平井产能模型研究”(YKJCX1620101)
李俊南(1990 — ),男,硕士研究生,研究方向为油藏工程及油气开发。
TE312
A
1673-1980(2016)06-0031-05
