基于修正相似度的User-Based协同过滤推荐算法

王竹婷 夏竹青 周艳玲

(合肥学院计算机科学与技术系， 合肥 230601)

基于修正相似度的User-Based协同过滤推荐算法

王竹婷 夏竹青 周艳玲

(合肥学院计算机科学与技术系， 合肥 230601)

运用传统的User-Based协同过滤算法计算用户相似度时，因数据过度稀疏而易造成较大的计算偏差。为了有效提高该算法的准确性，研究改进相似度计算方法。根据用户现有的评分数据计算每个项目的自信息量，根据自信息量为不同的项目分配权值，利用权值来修正传统的相似度计算方法。当用户共同评分项目数量较少时，增加惩罚因子，以避免评分相似所致相似度过高的问题。

推荐系统； 协同过滤； 相似度； 自信息量； 平均绝对偏差

0 前 言

推荐系统的主要功能是，根据网络用户在线消费及浏览行为历史数据进行用户的消费偏好分析及感兴趣商品预测，为用户提供个性化推荐信息。 优秀的推荐系统，可以使用户在信息过载的情况下准确获取所需信息，也可以使企业精准地向潜在客户展示自身形象。个性化推荐系统目前已广泛应用于各类电子商务网站、社交网站及门户网站。推荐系统中常用的协同过滤算法成为当前研究的热点问题。

推荐系统的协同过滤算法可以分为基于近邻 (Neighborhood-Based)的算法和基于模型 (Model-Based)的算法两大类[1-2]。基于模型的推荐算法利用了统计学或机器学习相关方法建立推荐模型，通过推荐模型进行预测。常用的建模方法包括朴素贝叶斯[3]、贝叶斯网络[4]、潜在因子分析[5]等。这些算法虽然在推荐系统中得到了一定程度的应用，但贝叶斯模型的建立需要处理除评分数据之外的大量语义信息，加重了系统的负担。通过奇异值分解(SVD)矩阵降维技术可以得到用户兴趣潜因子和项目潜因子，但会有部分信息丢失，从而影响推荐效果。

基于近邻的推荐算法又可细分为基于用户[6](User-Based)的算法和基于项目[7](Item-Based)的算法。基于用户的推荐算法，首先利用了用户的历史评分数据，计算出目标用户与其他用户之间的相似度，选择相似度高的用户作为近邻用户，再将近邻用户感兴趣项目推荐给目标用户。基于项目的推荐算法，则先是计算项目之间的相似度，然后再找出与目标用户感兴趣的项目相似度较高的项目予以推荐。

运用基于近邻的推荐算法时，无须获知用户或项目属性信息，仅通过分析历史评分数据即可实施推荐。该算法在实际推荐系统中得到了最为广泛的应用，但也存在数据稀疏性、冷启动和扩展性等方面的问题。

本次研究针对传统的用户相似性度量方面存在的缺陷，提出一种修正的相似性度量算法。根据每个项目的受用户欢迎程度为其赋予不同的权值，对传统的相似度算法予以修正，为共同评分项目数过少的用户设计惩罚因子。MovieLens数据集测试结果证明，改进后的相似性度量公式可以在一定程度上修正因数据稀疏性而导致的相似度计算结果偏差，从而改善User-Based协同过滤算法推荐效果。

1 User-Based协同过滤算法

分步执行User-Based协同过滤算法：建立用户兴趣模型；根据用户兴趣模型计算出用户之间的相似度，并选择相似度高的用户作为近邻用户；根据近邻用户感兴趣的项目预测目标用户对这些项目感兴趣的程度，再执行推荐。

1.1 用户兴趣推荐模型

设系统中有m个用户和n个推荐项目，用户集合为U={U1,U2,…，Ui，…,Um}，项目集合为I={I1,I2,…，Ij，…,In}，用户的历史评分数据通过用户-项目评分矩阵表示(见表1)。表1中，Rij为用户i对项目j的评分。

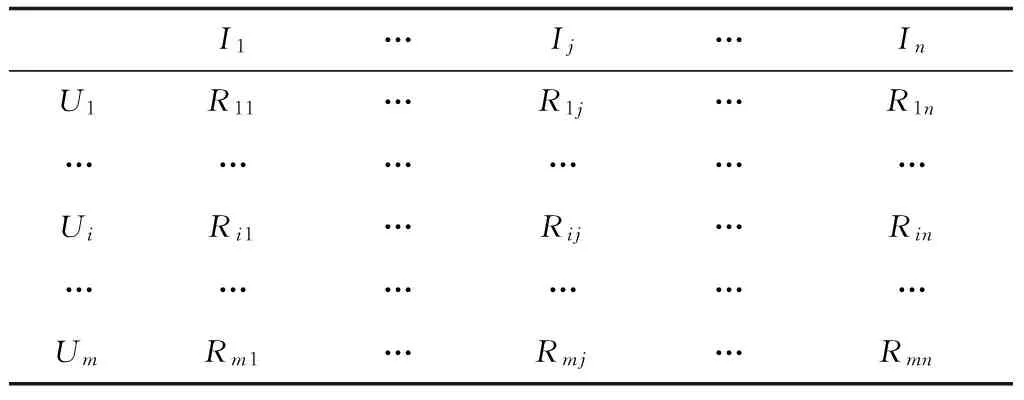
表1 用户-项目评分矩阵

在用户-项目评分矩阵中，行向量反映的是同一用户对不同项目的评分数据。User-Based推荐算法则是通过用户共同评分项目的评分差异来度量用户间的相似性。但实际推荐系统中，用户评分项目往往非常有限，用户-项目矩阵存在大量空缺值，难以准确描述用户的兴趣爱好。

1.2 相似度计算方法

相似度计算结果决定了近邻集合的选择和最终的推荐结果预测，在整个推荐过程中起到了至关重要的作用。传统的相似度计算方法包括余弦相似性、修正的余弦相似性、Pearson相关系数、Jaccard相似性系数等[8]。总体来说，修正的余弦相似性和Pearson相关系数推荐的精度更高。

(1) 修正的余弦相似性。余弦相似性是将用户在n个项目上的评分数据视为一个n维向量，通过计算用户n维空间向量的夹角余弦值来度量用户间的相似度。但余弦相似性没有考虑到不同用户在评分习惯上的差异性，衡量效果不够理想。修正的余弦相似性则通过用户评分值减去该用户的平均评分值所得到的偏差来改善不同用户的评分差异性。通过式(1)计算：

(1)

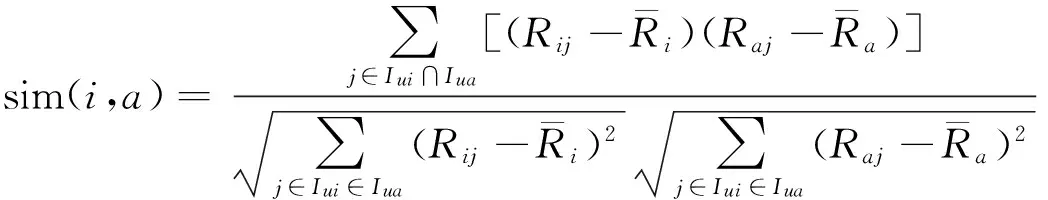
(2)

与式(1)不同的是，式(2)中分母部分只计算用户共同评分项目偏差和的乘积。

1.3 相似度计算方法缺陷

运用余弦相似性方法在计算用户相似度时，先将用户未评分项目标记为0，再将评分数据带入公式计算。而用户-评分矩阵的极度稀疏是由于用户购买能力有限所造成的， 并非是对未评分项目不感兴趣，用0标记未评分项显然与实际情况不符。运用Pearson相关系数方法计算时，则只考虑用户共同的评分项目，当共同评分项目过少时不足以衡量用户间的相似性。

2 基于自信息量修正的相似度计算方法

2.1 自信息量

Shannon在1948年提出并发展了信息论的观点，主张用数学方法度量和研究信息，并提出自信息量的概念[9]。自信息量是对离散信源发出信号不确定性的一种度量，自信息量越大，不确定性也越大。计算公式如式(3)所示：

Inf(ai)=log2p(ai)

(3)

式中：ai的自信息量为Inf(ai)；p(ai)是取值为ai的概率。

2.2 项目自信息量

在推荐问题中，项目自信息量反映的是该项目能否得到用户认可的不确定性，通过式(4)、(5)来计算：

(4)

Inf(Ii)=log2p(Ii)

(5)

式中：p(Ii)表示项目i被用户接受的概率；Fre(Ii)表示项目i被用户评分的次数；Pop(Ii)表示对项目i的评分高于用户平均评分的次数。Inf(Ii) 是项目i的自信息量，自信息量越高表示项目能够被用户接受的不确定性越大，越符合噪声项目的特征。

2.3 修正的相似度计算方法

Pearson相关系数通过计算用户共同评分项目的评分差异来衡量用户间的相似程度。所有的项目在衡量用户相似度时所产生的影响力是均等的，忽略了噪声数据的干扰及用户间共同评分的项目数量对相似度的影响。

为提高相似度计算方法的精度，在Pearson相关系数计算公式的基础上为每个项目增加权值，权值大小由项目的自信息量决定。自信息量越大的项目，越符合噪声项目的特征，权值也应适当减小。自信息量越小的项目则越受用户欢迎，越能代表用户的兴趣爱好，权值应适当增加。项目权值通过式(6)来计算：

(6)

式中：wi是项目i的权值；Infmax和Infmin分别为所有项目中自信息量最大值和最小值。式(7)为本次研究所提出的改进后的相似度计算方法。

(7)

(8)

式中：| Iui∩Iua|为用户i和用户a的共同评分项目数；T为事先设定好的阈值。

3 基于用户的协同过滤推荐

利用上述改进方法计算用户间的相似度，根据用户相似度确定目标用户的最近邻居集，通过近邻用户对目标项目的评分值进行预测。计算方法如式(9)所示：

(9)

式中：Pui为用户u对项目i的预测评分；NBu为用户u的近邻集。

4 实验结果及分析

4.1 数据集

采用GroupLens研究小组提供的MovieLens数据集ml-100k，对改进后的相似度计算方法进行评估测试。该数据集包含7组数据，每组数据分为训练集和测试集。其中，训练集中包括943名用户对1 682部电影的100 000项评分数据，评分值的取值范围为1～5，每位用户至少有20个评分项。通过训练集数据来预测用户对未评分项目的评分值，再对预测结果与测试集数据进行对比分析。

4.2 评估标准

以平均绝对偏差MAE作为评估算法推荐质量评价指标，其计算方法如下：

(10)

(11)

式中：pij为通过训练集产生的预测评分；qij为测试集提供的实际评分；Ni为测试集提供的用户i的评分项目数量；MAEi为用户i对Ni个项目预测评分的平均绝对偏差；M为全体用户总数；MAE为全体用户的平均绝对偏差。MAE的值越小，算法预测的结果与实际评分值越接近，算法推荐的准确性也越高。

4.3 实验结果对比

本次研究所提出的相似性度量方法，是在Pearson相关系数的基础进行了改进。为验证改进策略的有效性，并确定参数T的最佳取值，设计实验进行对比。分别将基于Pearson相关系数 (PCC)、自信息量修正相似性 (IPCC)和加惩罚因子的自信息量修正相似性 (WIPCC)这3种度量方法与User-Based推荐算法相结合，比较改进策略对推荐结果产生的影响。

与传统的Pearson相关系数相比，自信息量修正的相似性度量方法在推荐质量上有较大的改进。图1所示为不同T值下的MAE结果对比。加惩罚因子的自信息量修正相似性在T值取3～9的情况下，可将MAE值改进到0.086～0.012。当T为4时，改进效果最佳。在后面的对比实验中，T全部取4。

User-Based协同过滤算法的推荐质量，在很大程度上还受近邻个数的影响，通常情况下近邻个数越多，推荐的准确率越高。为验证本算法在不同近邻个数下实施推荐的有效性，将实验中近邻个数从10依次递增到100，比较其与传统的Pearson相关系数(PCC)和修正的余弦相似性(AC)推荐结果的MAE值。图2 所示为3种算法在不同近邻个数下的MAE结果对比。

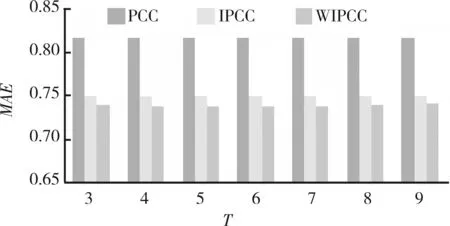
图1 不同T值下的MAE结果对比

图2 3种算法在不同近邻个数下的MAE结果对比

由图(2)可知，修正相似度计算方法优于传统的Pearson相关系数和修正的余弦相似性，在近邻个数较少时推荐质量尤为明显，具有更高的稳定性。

4.4 实验结果分析

传统的Pearson相关系数仅仅通过用户的共同评分项目计算相似度，会因为数据的极端稀疏造成共同评分项目数过少，且又受到噪声项目的影响，导致计算结果与实际情况出现较大偏差。

修正的余弦相似性虽然整体推荐质量优于Pearson相关系数，但其在近邻数量低于30时表现出的性能并不理想。从计算公式中，不难发现其分母项将用户各自的评分项都纳入计算，分子项中却只有共同评分项。因此，余弦相似性的整体计算结果偏低，用户近邻数量少，推荐效果不稳定。

本次提出的修正相似度计算方法，以Pearson相关系数为基础，不存在余弦相似性计算结果偏低的缺陷；同时针对Pearson相关系数存在的问题进行修正，为用户共同评分项目数设置阈值，并对所有项目根据其自信息量确定权值，削弱噪声项目的不利影响，有效提高了协同过滤算法的推荐质量。

5 结 语

针对User-Based协同过滤推荐算法，提出了一种新的衡量用户间相似性的度量方法。该方法以传统的Pearson相关系数为基础，在计算相似度前首先计算每个项目的自信息量。自信息量越大表示该

项目被用户接受的不确定性越大，那么其确认为噪声项目的可能性也越大。根据自信息量的大小为项目分配不同的权值，对于用户受欢迎的项目，增加其在相似度计算时的权重，对于噪声项目则削弱其在相似度计算时产生的不利影响。在用户共同评分项目极少的情况下，在相似度值计算过程中加入了惩罚因子，以避免极少数项目评分相似而使相似度过高的问题。利用MovieLens数据集对本次改进算法和传统的相似性度量方法进行测试，测试结果证明改进算法在一定程度上克服了数据稀疏性和噪声数据的影响，取得了较好的推荐效果。

[1] SHI Y,LARSON M,HANJALIC A.Exploiting User Similarity Based on Rated-Item Pools for Improved User-Based Collaborative Filtering[C]∥Proc of the 3rd Acm Conf on Recommender Systems.2009:125-132.

[2] LU J,WU D S,MAO M S,et al.Recommender System Application Developments: a Survey [J].Knowledge-Based Systems ,2015,74:12-32.

[3] 李大学,谢名亮,赵学斌.基于朴素贝叶斯方法的协同过滤推荐算法[J].计算机应用，2010,30(6):1523-1526.

[4] YEUNG C K F,YANG Y Y,NDZI D.A Proactive Personalized Mobile Recommendation System Using Analytic Hierarchy Process and Bayesian Network [J].Journal of Internet Services and Applications,2012,3(2): 195-214.

[5] PATEREK A.Improving Regularized Singular Value Decomposition for Collaborative Filtering[C]∥Proceeding of KDD Cup Workshop at 13th ACM Int.Conf.on Knowledge Discovery and Data Mining.2007: 39-42.

[6] HERLOKCER J L,KONSTAN J A,BORHCESR A,et al.An Algorithmic Framework for Performing Collaborative Filtering[C]∥Proceedings of SIGIR99 :22nd International Conference on Research and Development in Information Retrieval.1999:230-237.

[7] SARWAR B,KARYPIS G,KONSTAN J,et al.Item-Based Collaborative Filtering Recommendation Algorithms[C]∥Proceedings of the 10th International World Wide Web Conference.2001:285-295.

[8] BIDYUT K P，RAIMO L，VILLE O，et al.A New Similarity Measure Using Bhattacharyya Coefficient for Collaborative Filtering in Sparse Data[J].Knowledge Based Systems,2015,82: 163-177.

[9] 廖芹，郝志峰，陈志宏.数据挖掘与数学建模[M].北京：国防工业出版社，2010:152-154.

[10] BREESE J S,HECKERMAN D,KADIE C.Empirical Analysis of Predictive Algorithms for Collaborative Filtering[C]∥ Proc 14th Conf on Uncertainty in Artificial Intelligence Conference.1998: 43-52.

A User-Based Collaborative Filtering Recommendation Algorithm Based on Modified Similarity

WANGZhutingXIAZhuqingZHOUYanling

(Department of Computer Science and Technology, Hefei University, Hefei 230601, China)

An improved method of similarity calculation is proposed in this paper because the traditional user-based collaborative filtering algorithm are not suitable in sparse data. First of all, we utilize the user′s rating data to calculate self information quantity of each item, which can be used to determine the weights of the item, and improved the traditional similarity measure. Then, we add a penalty factor to avoid the high similarity caused by the fewer similar rating behavior when the number of co-rated items is few.

recommendation system; collaborative filtering; similarity; self information quantity; mean absolute error

2016-03-16

安徽省教育厅自然科学资助项目“基于上下文相关性的网络编码可靠多播技术的研究”(KJ2016A609)；合肥学院科研发展基金资助项目“面向电子商务的个性化推荐系统研究”(14KY11ZR)；合肥学院重点建设学科资助项目(2014XK08)；合肥学院学科带头人培养对象资助项目(2014DTR08)

王竹婷(1984 — )，女，硕士，助理实验师，研究方向为人工智能与数据挖掘。

TP301

A

1673-1980(2016)06-0075-05