多矢量水听器低频近场目标协同定位算法*

张超然，程锦房，肖大为

(1. 海军装备研究院 标准规范研究所， 上海 200235； 2. 海军工程大学 兵器工程系， 湖北 武汉 430033)

多矢量水听器低频近场目标协同定位算法*

张超然1，程锦房2，肖大为2

(1. 海军装备研究院 标准规范研究所， 上海 200235； 2. 海军工程大学 兵器工程系， 湖北 武汉 430033)

针对水下小平台难以实现低频近场目标定位的问题，研究了基于多个矢量水听器的协同定位算法。算法将多个矢量水听器视为不同的观测点，利用矢量水听器阵列流型特点估计出目标相对于不同观测点的方位角，根据这些方位角信息利用正交矢量算法对近场目标进行定位，避免了多维搜索过程，减少了计算量。仿真结果表明，算法能够准确地定位低频近场目标，有效地提高定位精度。

近场定位；矢量水听器；纯方位估计；正交矢量算法

水下目标定位在水中兵器领域应用广泛，而低频声信号在水中衰减较小，在水下定位中扮演着重要的角色。但是低频信号的波长较大，为了保证良好的分辨率以及定位精度，定位所需的阵列长度非常大，水下小平台一般难以实现；此外水中兵器的控制范围有限，当目标靠近时，远场平面波模型往往不再适用，也就是说目标常常处于阵列的近场范围内。所以基于水下小平台的近场低频目标定位研究具有重要的应用价值。

以往的近场定位算法主要利用的是声压阵，声压阵近场定位是远场定位的扩展，包括二维多重信号分类(MUltiple SIgnal Classification，MUSIC)算法、三维MUSIC算法、近场最大似然算法等[1-3]。与远场情况不同的是，近场定位需要估计的参数个数增加，远场定位算法需要的单维搜索在近场情况下变为了多维搜索，这大大增加了计算量，使得很多算法难以实现。针对这个问题，近期多种分步估计算法被提出，比如Two-stage MUSIC算法、Mixed-order MUSIC算法、二阶旋转不变子空间(Estimation of Signal Parameters via Rotational Invariance Techniques， ESPRIT)算法以及二阶非圆信号定位算法等[4-7]。这些算法利用Fresnel近似[8]，将方位角与距离参数进行分离，然后进行逐步估计。但是这些算法只能应用于中心对称阵列[9]，并且往往需要利用高阶累计量[10]，应用范围较小。

在小平台定位研究方面，由于尺寸的限制，阵列的孔径不能很大。矢量水听器是一种新型传感器，可以同时、共点测量声场的声压以及三轴质点振速分量[11]。单个传感器就可以实现目标的方位估计[12]，不受尺寸的限制，而且由于在近场情况下声阻抗与信号的距离有关，所以单个矢量水听器就能够完成对近场目标的距离估计[13]。但是，与声压阵相似，单矢量水听器在近场定位时同样需要多维搜索，而且定位精度随着距离的增加会严重下降。另外，利用多个矢量水听器测向能力对目标进行定位的算法有测向交叉算法以及三角定位算法等，这类算法根据单矢量水听器估计得到目标的方位角，然后利用水听器与目标的几何关系解算出目标的位置。这类算法没有充分利用各矢量水听器之间的协同关系，容易出现虚假目标；为了避免较大的定位误差，这一类算法一般要求水听器之间具有较远的距离[14]，从而导致定位系统的尺寸过大。所以基于小平台的近场低频目标定位研究需要考虑平台大小、计算量以及定位精度的权衡问题。本文提出一种基于多个矢量水听器的近场目标协同定位算法。

1 近场模型

1.1 近场阵列模型

当目标位于阵列近场范围内，平面波模型已经不再适用，此时信号应被视为球面波。图1为近场信号的二维示意图。

图1 近场信号示意图Fig.1 Spatial geometry of near-field signal

如果以阵元1为参考阵元，r1,n为声源n到阵元1的距离，θ1,n为声源n到阵元1的方位角。根据球面波的传播方式，可以得到线阵的近场阵列转向矢量：

(1)

式中，rm,n为声源n到第m个阵元的距离，M为阵元个数。利用声压阵对近场信号进行定位与远场方位估计相似。以子空间类算法为例，将协方差矩阵通过特征分解，可以分为互相正交的信号子空间Ups与噪声子空间Upn。由于信号子空间与噪声子空间正交，可知信号的导向矢量与噪声子空间正交，由此可以得到二维MUSIC空间谱估计为：

(2)

其中ap(r,θ)与式(1)具有相同的形式，通过对距离以及角度的二维搜索就可以得到估计的空间谱，所得的峰值对应了信号的位置。

1.2 近场单矢量水听器模型

当声波为球面波时，假设声源产生的是单频信号，则简谐球面波声压可以表示为：

(3)

式中，w为信号角频率，k为波数，P为信号的幅度，r为距离。根据声场欧拉方程，可以求得近场声阻抗为[15]：

(4)

式中，λ为波长，ρ为介质的密度，c为声速，ρc为常数，可以看出近场声阻抗与信号波长以及传播距离有关，当传播距离远大于波长时，声阻抗的虚部可以忽略，与远场声阻抗相同。

考虑二维矢量水听器，其接收的数据为：

(5)

av(θ,r)=[cosθ,sinθ,1/f(r)]T

(6)

与近场声压阵相似，其阵列流型在近场时与方位角和距离有关，可以用于近场定位。同样可以将协方差矩阵分为信号子空间Uvs与噪声子空间Uvn，并利用正交关系得到单矢量水听器近场二维MUSIC方位谱为：

(7)

综上所述，可以得到多矢量水听器近场测量得到的数据为：

y(t)=As(t)+ζ(t)

(8)

式中，s(t)=[s1(t),s2(t),…,sn(t)]T为源信号组成的信号矢量，ζ(t)为噪声矢量。如果有N个信号入射，则阵列流型具有如式(9)所示形式。

A=[a(θ1,1,r1,1),a(θ1,2,r1,2),…,a(θ1,N,r1,N)]

(9)

式中，

(10)

2 多矢量水听器协同定位算法

前文介绍的近场定位算法是远场定位算法在近场的直接推广。虽然可以有效地定位目标的位置，但是由于近场情况下阵列流型与距离有关，导致了需要估计的参数增加，使得搜索的维度增加，这大大地增加了算法的计算量，在很多实际应用中难以实现；其次，两种方法的精度不高，随着频率的降低、距离的增加，这种现象更加严重。本节介绍基于多个矢量水听器的协同定位算法。协同定位算法分为两步，首先利用多水听器对目标的方位角进行估计。由于在矢量水听器的阵列流型中，相同的水听器振速通道之间的比值与频率无关，这就使得当目标频率降低时，方位估计的精度不受影响。然后利用多个矢量水听器估计得到的方位角，根据纯方位角估计中的正交矢量方法，估计出目标的位置。

文献[16]利用数据的时间旋转不变性，提出了单矢量水听器ESPRIT算法，该算法不需要进行搜索，且在距离未知的情况下能够直接计算出目标的方位角。本文将这种方法用于多矢量传感器，假设目标为单频信号，而且信号频率分别为f1,f2,…,fN，将多矢量水听器的测量数据与延时后的数据组成新的数据：

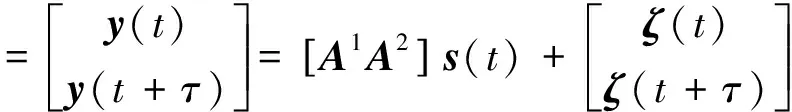
(11)

式中，

(12)

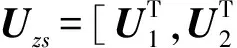
(13)

式中，T为非奇异矩阵，引入变换矩阵Ψ，定义Ψ=T-1ΦT，则有：

U1Ψ=U2

(14)

根据最小二乘法或者加权最小二乘法可以求出Ψ的估计值。由于Φ为对角矩阵，则Φ对应了Ψ的特征值矩阵，而T-1对应Ψ的特征向量。所以对Ψ进行特征分解并利用式(13)就可以得到阵列流型A的估计值。

由于A包含了目标的方位角信息，根据式(6)和式(10)可以看出，阵列流型A中av(θm,n,rm,n)的前两项只与角度有关，所以可以利用式(15)求出各目标相对于不同水听器的角度：

(15)

式中：m=1,2,…,M；n=1,2,…,N；[A]m,n表示A的第(m,n)个元素。每一个目标对应了M个方位角，在近场条件下这些角度是不同的。得到这些角度信息之后，目标的定位可以看作是多个观测站点的纯方位角定位问题，对于这个问题可以采用正交矢量算法来估计目标的距离[17]。当然，除了以上方法外，也可以利用其他的算法对各个矢量水听器的方位角信息进行估计。

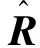
q=Rm,n+om

(16)

(17)

式中，em,n为垂直误差矢量，它与观测矢量垂直，可以求出：

(18)

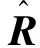
(19)

将对应于目标n的一组观测矢量写成向量的形式，可以表示为：

Bq=o⊥+c

(20)

式中，

(21)

对于式(20)，可以利用最小二乘法或者加权最小二乘法求得q的估计值，所以正交矢量方法得到目标n的位置估计为：

(22)

值得注意的是：一组观测矢量对应了一个指定的目标，这就避免了纯方位角估计中对于多目标情况常遇到的数据联合问题[18]。另外，由于M个阵元对应了3M个数据通道，所以本文方法最多可以定位3M-1个目标。

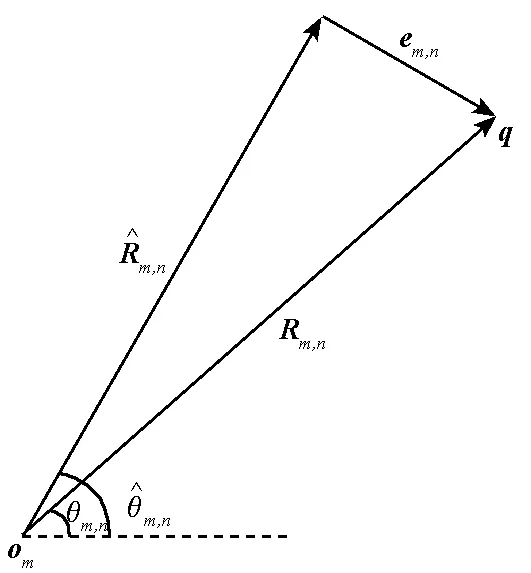
图2 观测矢量与目标的关系Fig.2 Relationship between the bearing vector and target

文献[14]推导了在纯方位角估计中测向误差对于定位误差的影响，与之相似，在本文算法中较小的测向误差会造成较大的定位误差。

3 算法仿真

为了验证算法的有效性，对本文算法进行仿真实验，并将定位结果与声压阵二维MUSIC近场定位算法、单矢量水听器二维MUSIC近场定位算法以及矢量阵聚焦波束形成算法进行比较。

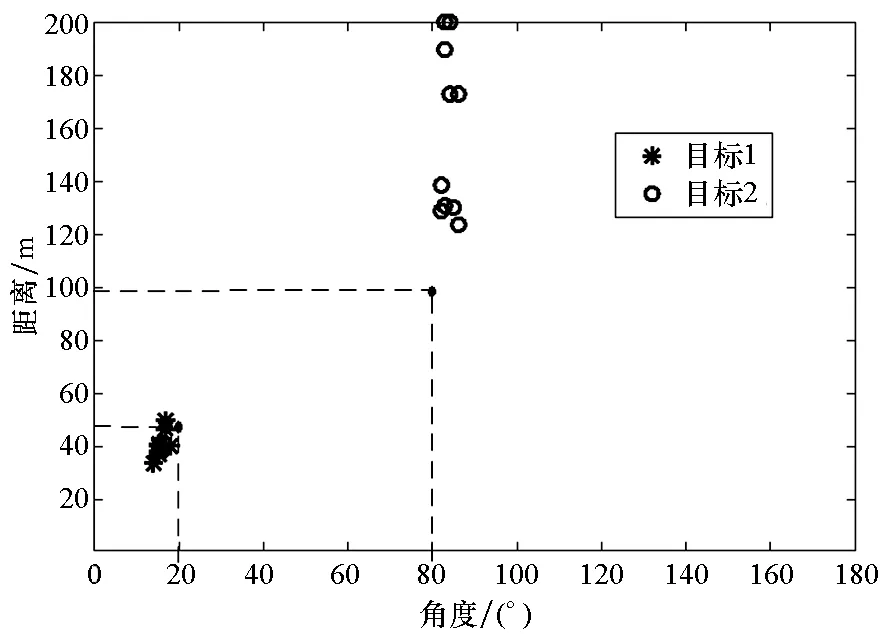
仿真1 利用算法对两个近场目标进行10次独立的定位。仿真条件为：阵元个数为6，阵元间距为1 m，信噪比为10 dB。两个目标的位置信息分别为：距离50 m，方位角20°；距离100 m，方位角80°。信号频率分别为50 Hz和60 Hz，采样个数为1000。表1为三种算法估计得到的目标定位结果。图3为三种算法估计得到的目标位置分布图，其中空心点是对于100 m处目标的定位结果，而星号是对于50 m处目标的定位。根据单矢量水听器对目标进行估计得到的结果可以看出，其对50 m处目标距离估计的效果要好于100 m处目标的，这是因为在距离较小时，距离对于声阻抗的影响较大，随着距离的变大，声阻抗随距离的变化越来越小，使得距离估计的偏差变大。根据声压阵对目标定位时得到的结果可以看出两个目标的定位都出现了明显的偏差，角度和距离的估计都有明显的误差，这是因为对于低频信号，声压阵不具有足够的孔径，从而使得估计的精度大大降低。本文算法的定位结果要比前两种方法精确，结果都收敛于真实值附近。

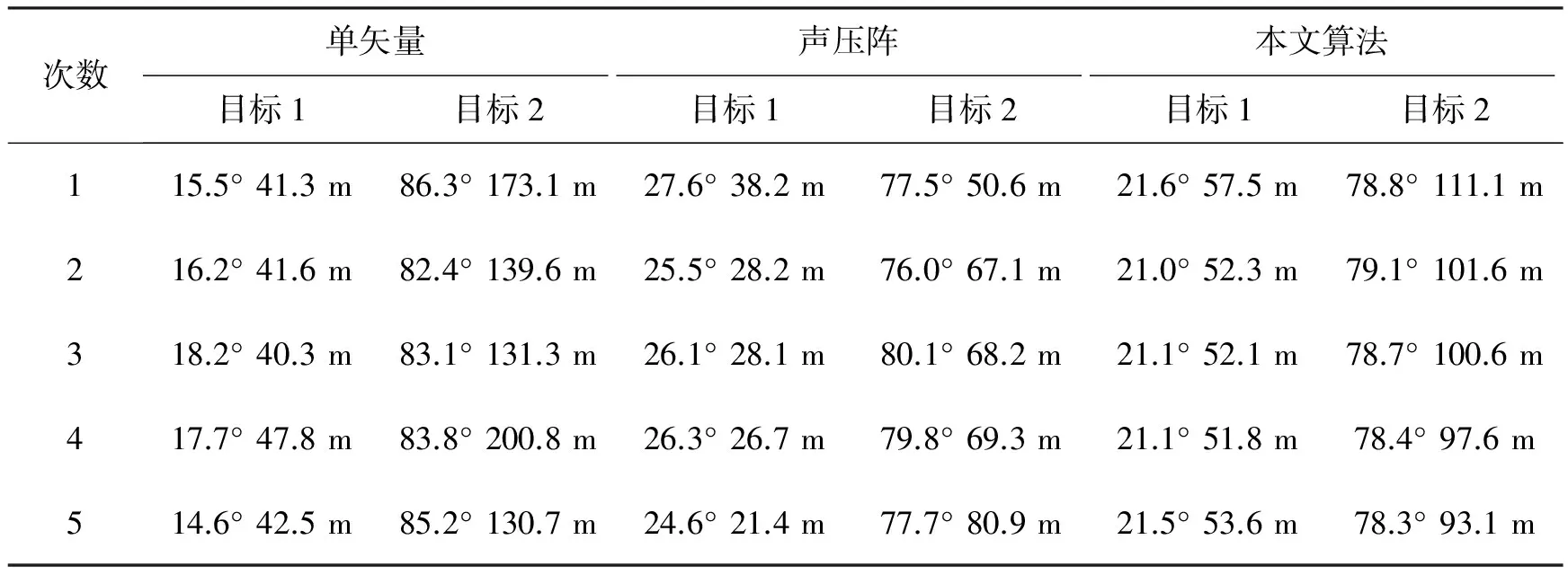
表1 各算法的定位结果Tab.1 Localization results by each algorithm

(a) 单矢量水听器定位结果(a) Localization results by single hydrophone

(b) 声压阵定位结果(b) Localization results by acoustic pressure array

(c) 协同定位结果(c) Localization results by cooperative method图3 三种算法的定位结果Fig.3 Localization results of different methods

仿真2 比较在不同信噪比(Signal Noise Ratio, SNR)情况下算法的均方根误差(Root Mean Square Error，RMSE)。仿真条件为：阵元数为6，阵元间距为1 m，对一个距离为50 m、方位角为80°的目标进行定位，信号频率为50 Hz，信噪比从0 dB到30 dB，每个信噪比进行200次蒙特卡洛实验，图4为各种算法对于目标方位角和距离估计的RMSE。从图中可以看出，声压阵与单矢量水听器二维MUSIC算法的定位精度相对较低；本文算法的定位精度优于矢量阵聚焦波束形成方法。另外，二维MUSIC算法和聚焦波束形成是基于二维搜索的，运算量随着搜索范围和搜索精度的增加而增加，而本文算法的解是闭式的，所需的计算时间远小于其他两种算法。

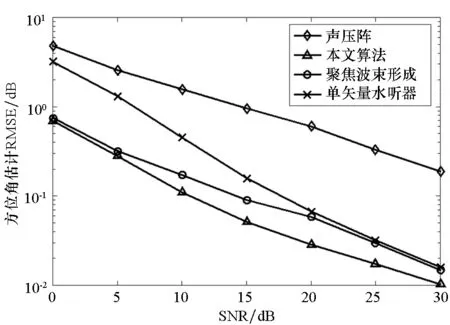
(a) 方位角估计的RMSE比较(a) Comparison of RMSE of azimuth estimations

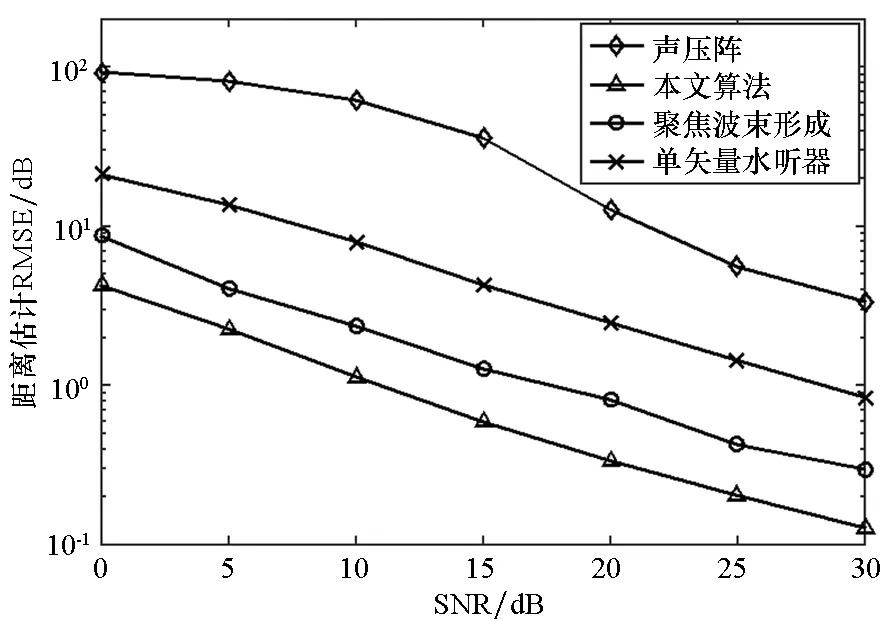
(b) 距离估计的RMSE比较(b) Comparison of RMSE of range estimations图4 不同信噪比下不同算法方位角和距离估计的RMSE比较Fig.4 RMSE of range and azimuth estimations vs. SNR

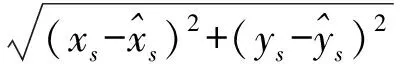
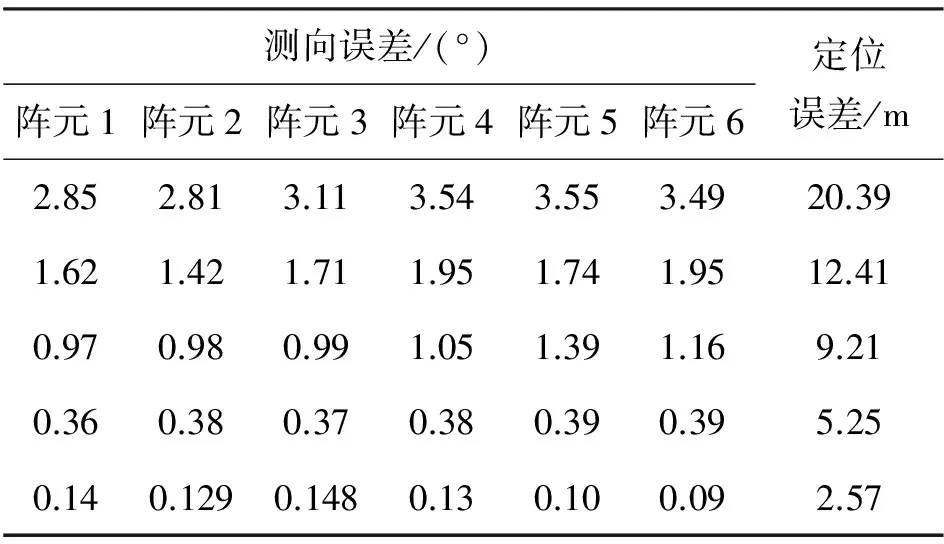
表2 各阵元的测向误差引起的定位误差Tab.2 Localization error caused by directions error

4 结论

本文研究了一种能够适用于水下小型平台的低频信号近场定位算法，算法解决了对于低频信号平台孔径过小的问题，提高了对近场低频目标的定位精度。算法给出了定位的闭式解，减小了近场定位的计算量。仿真结果表明，本文算法能够完成低频近场目标的精确定位，其保留了矢量水听器定位的优势，而且增加了距离参数定位的准确性。

References)

[1] Huang Y D, Barkat M. Near-field multiple source localization by passive sensor array[J]. IEEE Transaction on Antennas Propagation, 1991, 39(7): 968-975.

[2] Hsien S H, Shun H C, Chieng H W. 3-D MUSIC with polynomial rooting for near-field source localization [C]//Proceedings of IEEE International Conference on Acoustic, Speech, and Signal Processing Conference Proceedings (ICASSP), New York: IEEE, 1996.

[3] Chen J C, Hudson R E, Kung Y. Maximum likelihood source localization and unknown sensor location estimation for wideband signals in the near-field[J]. IEEE Transaction on Signal Processing, 2010, 50(8): 1843-1854.

[4] Liang J, Liu D. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transaction on Signal Processing, 2010, 58(1): 108-120.

[5] Wang B, Zhao Y P, Liu J J. Mixed-order MUSIC algorithm for localization of far-field and near-field sources [J]. IEEE Signal Processing Letters, 2013, 20(4): 311-314.

[6] Jiang J J, Duan F J, Chen J, et al. Mixed near-field and far-field sources localization using the uniform linear sensor array [J]. IEEE Sensor Journal, 2013, 13(8): 3136-3143.

[7] Xie J, Tao H H, Rao X, et al. Efficient method of passive localization for near-field noncircular sources [J]. IEEE Antennas and Wireless Propagation Letters, 2013, 14: 1223-1226.

[8] Yuen N, Friedlander B. Performance analysis of higher order ESPRIT for localization of near-field sources[J]. IEEE Transaction on Signal Processing, 1998, 46(3): 709-719.

[9] Liu G H, Sun X Y. Efficient method of passive localization for mixed far-field and near-field sources [J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12: 902-905.

[10] Liang J. Joint azimuth and elevation direction finding using cumulant[J]. IEEE Sensor Journal, 2009, 9(4): 390-398.

[11] 梁国龙, 张锴, 付进, 等. 单矢量水听器的高分辨方位估计应用研究[J]. 兵工学报, 2011, 32(8): 986-990. LIANG Guolong, ZHANG Kai, FU Jin, et al. Research on high-resolution direction-of-arrival estimation based on an acoustic vector-hydrophone [J]. Acta Armamentarii, 2011, 32(8): 986-990.(in Chinese)

[12] 陈川. 基于水下小平台的被动声探测定位技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. CHEN Chuan.Research on passive acoustic detection and localization with small underwater platform [D]. Harbin: Harbin Engineering University, 2013.(in Chinese)

[13] Wu Y I, Wong K T , Lau S K . The acoustic vector-sensor′s near-field array-manifold [J]. IEEE Transaction on Signal Processing, 2010, 58(7): 3946-3951.

[14] 张宇, 孙大军, 吕云飞, 等. 矢量水听器双潜标系统纯方位定位精度分析[J]. 哈尔滨工程大学学报, 2010, 31(7): 868-871. ZHANG Yu, SUN Dajun, LYU Yunfei, et al. Analysis of location precision when using a dual subsurface-buoy system with a vector hydrophone [J]. Journal of Harbin Engineering University, 2010, 31(7): 868-871.(in Chinese)

[15] 惠俊英, 慧娟. 矢量声信号处理基础[M]. 北京: 国防工业出版社, 2009. HUI Junying, HUI Juan.Fundamentals of vector acoustic signal processing [M]. Beijing: National Defense Industry Press, 2009.(in Chinese)

[16] Tichavsky P, Wong K T, Zoltowski M D. Near-field/far-field azimuth and elevation angle estimation using a single vector hydrophone[J]. IEEE Transaction on Signal Processing, 2001, 49(11): 2498-2510.

[18] Griffin A, Alexandridis A, Pavlidi D, et al. Localizing multiple audio sources in a wireless acoustic sensor network[J]. Signal Processing, 2015, 107: 54-67.

Cooperative localization of low-frequency near-field target using multi-vector-hydrophones

ZHANG Chaoran1, CHENG Jinfang2, XIAO Dawei2

(1. Institute of Specifications and Standards, Naval Academy of Armament, Shanghai 200235, China；2. Department of Weapon Engineering, Naval University of Engineering, Wuhan 430033, China)

Aiming at the problem that the underwater small platform cannot locate the low-frequency near-field target, a cooperative localization algorithm using multiple vector hydrophones was proposed. The hydrophones were regarded as different observation points, and then the azimuth angles of target connected to different observation points were estimated respectively on the basis of the array manifold characteristics of hydrophones. According to these azimuths, the location of near-field target was realized by using the orthogonal vector method. This algorithm avoids the multi-dimensional search process and reduces the calculation. The simulation results show that this algorithm can locate the near-field target accurately and improve the location accuracy effectively.

near-field localization; vector hydrophone; bearing-only estimation; orthogonal vector method

10.11887/j.cn.201606029

2015-07-24

国家部委基金资助项目(4010709010201)

张超然(1988—), 男, 浙江衢州人，工程师，博士，E-mail：zhangchaoran@yeah.net； 程锦房(通信作者), 男, 教授，博士，博士生导师，E-mail：jeffreychangcn@hotmail.com

TN911.7

A

1001-2486(2016)06-180-06

http://journal.nudt.edu.cn