电磁轨道发射器动态发射过程的数值模拟*
2017-01-07鲁军勇龙鑫林
谭 赛,鲁军勇,张 晓,龙鑫林
(海军工程大学 舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)
电磁轨道发射器动态发射过程的数值模拟*
谭 赛,鲁军勇,张 晓,龙鑫林
(海军工程大学 舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)
针对电磁轨道发射器动态发射过程的数值模拟问题,基于矢量磁位A和时间积分标量电位V,采用节点单元法,并选择运动坐标系描述运动问题,推导出动态发射下的电磁轨道发射器三维涡流场有限元离散方程。结合温度场控制方程,建立电磁轨道发射器的三维电磁-温度耦合有限元模型。针对一个电磁轨道发射器动态发射问题,对模型进行数值模拟,得到了动态发射下轨道及电枢的温度场分布特点及发射器电感梯度随时间的变化规律。计算结果表明,模型计算出的脉冲电流峰值、出口电流大小、出口速度等参数均与试验结果吻合较好,验证了所开发的有限元程序代码的正确性。
动态发射;电枢;电磁轨道发射装置;电感梯度;有限元
在脉冲电流的驱动下,电磁轨道发射器中的电枢在两轨道间作加速运动,电枢与轨道存在着滑动电接触,电枢的高速运动对轨道及电枢内部的磁场、电流分布具有显著的影响,这种现象称之为速度趋肤效应[1-4]。这种效应将导致转捩等一系列现象的发生,严重影响轨道的寿命。因此,电磁轨道发射器动态发射过程的数值计算一直是国内外学者研究的热点。然而,滑动电接触问题具有其自身的特殊性,主要表现为:运动分界面处需同时满足磁场强度H、磁感应强度B、电场强度E、电流密度J等四个物理量的分界面条件。
为解决这一类滑动电接触问题,一部分学者采用基于有限差分法建立了二维状态下的电磁场、温度场数学离散模型,分析了电枢运动下的电流分布特点[5-6]。然而,由于传统有限差分法的固有缺点,难以对复杂结构的电枢进行精确的分析。
一部分学者基于节点元法,在两个不同导体的分界面处采用双节点法,选择非连续的矢量磁位A处理电枢的运动问题[7-8]。但这种方法并未在三维运动涡流问题中得到验证;另一部分学者利用棱边元法,选取H作为求解量,建立了电磁轨道发射器的三维有限元模型[9-10],并引入迎风因子处理电枢运动问题,在考虑电枢运动的同时,保持了网格拓扑结构不变。然而,由于迎风因子的引入,电枢速度较大时导致的Peclet数增大会严重影响模型的收敛性和准确性。美国Hsieh等学者开发了具备进行电磁轨道发射器动态发射下的多物理场数值计算能力的三维机电分析程序代码(Electro-Mechanical Analysis Program in three Dimensions, EMAP3D)有限元程序代码[11]。此后,EMAP3D分别通过与三维显式动力学程序代码(DYNAmic in three Dimensions, DYNA3D)耦合、引入弹塑性本构模块,弥补了电枢的刚体假设不足[12-15],针对计算规模需求不断增加的需求,EMAP3D又推出了并行计算版本,使其仿真效率大幅提升[16-17]。目前,EMAP3D已经比较完备,是迄今为止较为成熟的一款电磁轨道发射器动态发射数值模拟软件。
但是,从文献[18]可以看出,EMAP3D在进行电磁轨道发射器动态发射的数值模拟过程中,仍存在电枢侧总电流计算值与实际电流激励值误差偏大的问题。因此,EMAP3D在处理枢轨接触面处的分界面条件上仍存在一定的不足。本文基于矢量磁位与标量磁位结合方法[19],推导出了电磁轨道发射器的三维运动涡流场有限元方程,最终建立了动态发射下的电磁轨道发射器的电磁-温度耦合模型。并针对一个电磁轨道发射器的动态发射问题进行了数值计算,将计算结果与EMAP3D程序计算结果、试验结果进行了对比分析。
1 电磁轨道发射器的控制方程
在有限元离散方程的推导及数值计算过程中,做如下基本假设:
1)电枢与轨道为理想接触,不考虑两者之间的接触电阻、摩擦力及材料的磨损;
2)电枢与轨道均视为刚体,忽略两者在电磁力作用下的形变。
1.1 三维运动涡流场控制方程
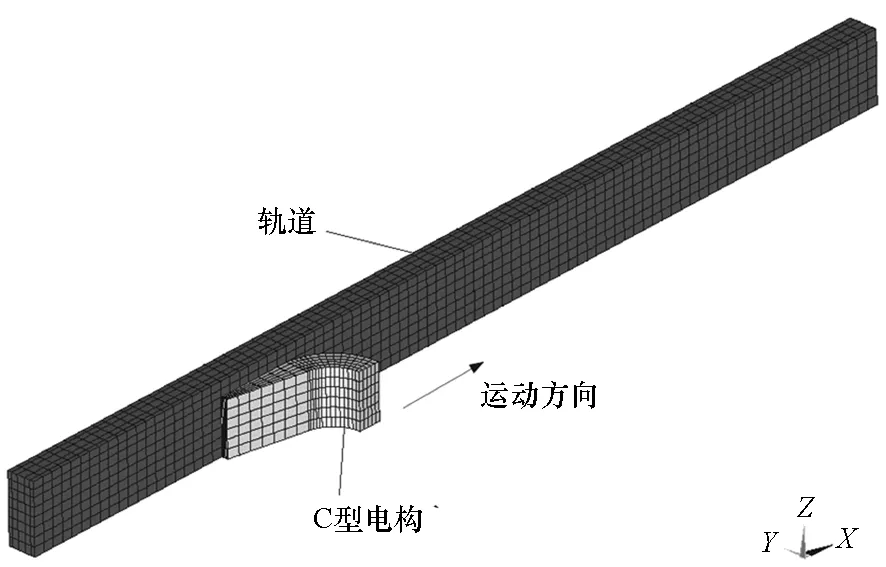
对于如图1所示的电磁轨道发射器三维求解域模型,考虑电枢运动的情况下,将求解域划分为运动部分和静止部分两大子区域。其中运动部分包括电枢及同侧的空气区域;静止部分包括轨道及同侧的空气区域。两大子区域分别采用独立的坐标参考系:对于运动部分,采用运动坐标系描述;对于静止部分,采用静止坐标系描述。采用A和标量电位φ作为变量,则整个求解域对应的控制方程可统一写为:
×(v×A)+σ
(1)
(2)
式中:v为磁阻率;σ为电导率。以上参数均与区域有关,比如σ在空气区域为零,在导体区域不为零。
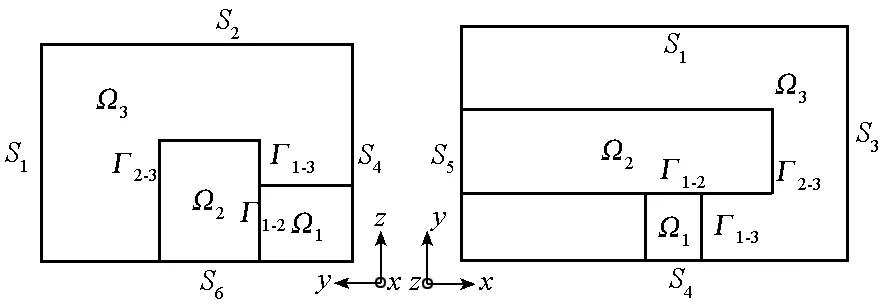
图1 电磁轨道发射器的三维求解域示意图Fig.1 Computational domains of electromagnetic rail launcher in three dimensions
对于运动区域,A对时间t的全导数与A对t的偏导数这两者之间的关系为:
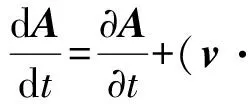
(3)
式中,v为导体的运动速度。显然,对于静止部分,A对t的全导数与A对t的偏导数相等。
引入时间积分标量电位V,则φ与V的关系为:
(4)
在如图1所示的求解区域中,分界面条件及边界条件采用A与V的描述形式为:
在Γi,j上
(5)
在Si上
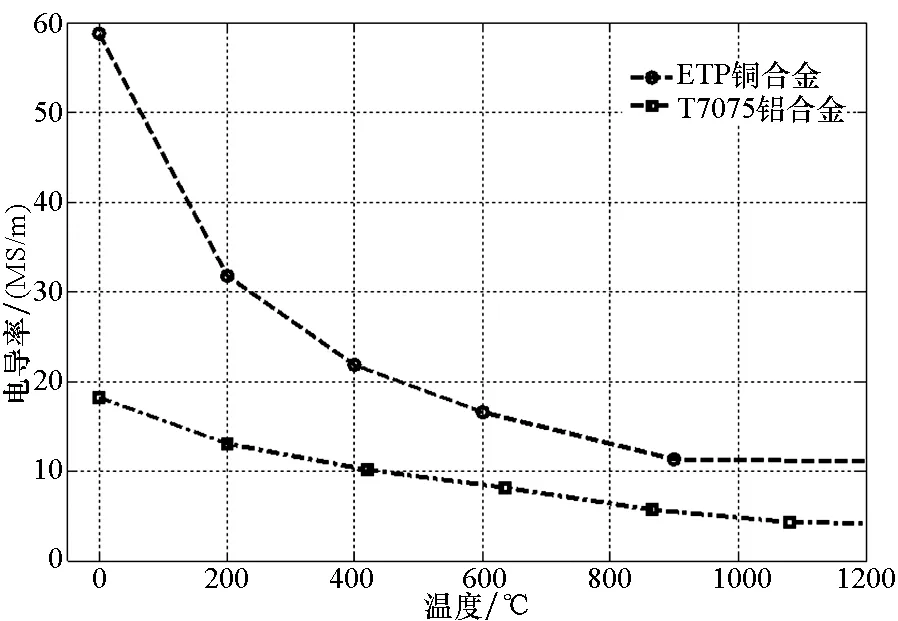
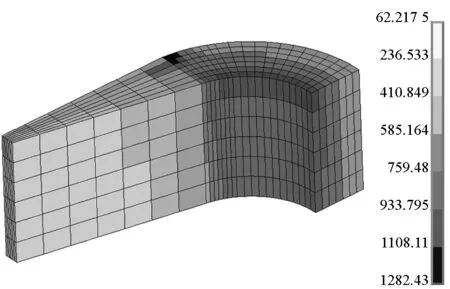
(6)
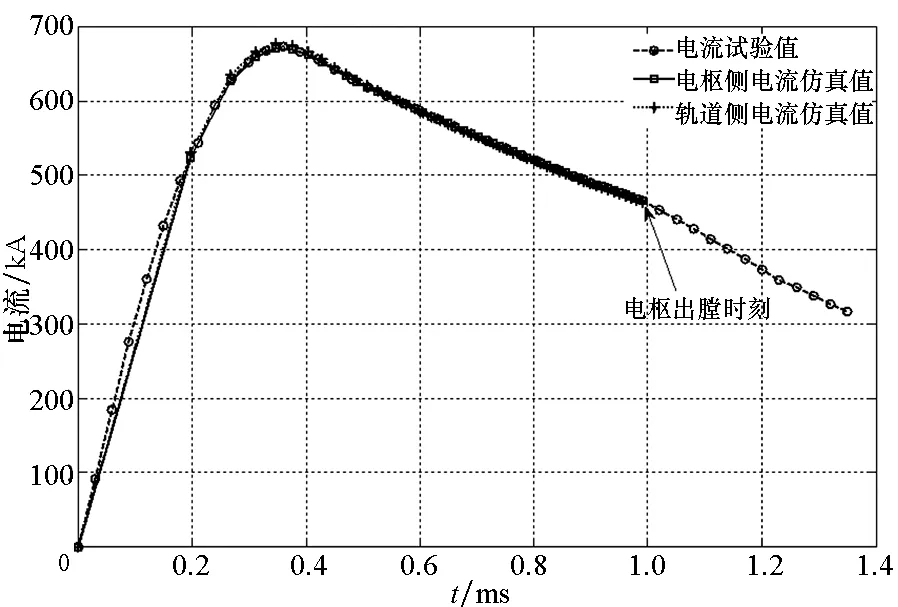
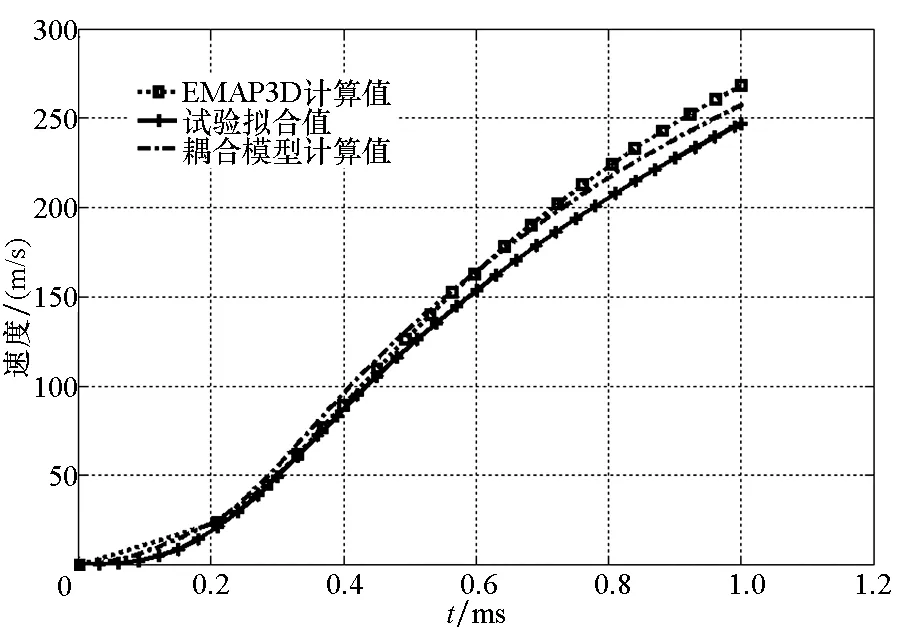
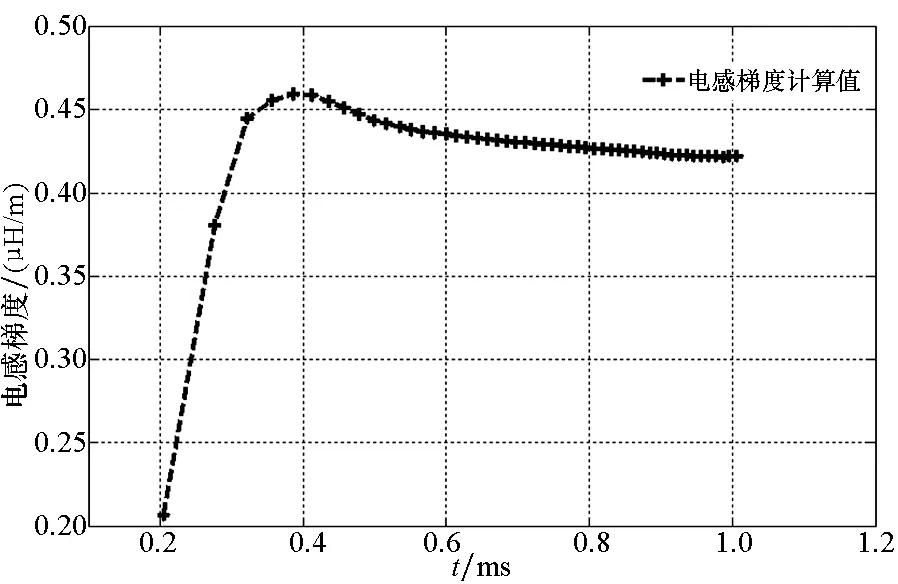
式中:nij表示区域Ωi与Ωj之间的分界面Γi,j的单位法向矢量;ni为边界面Si上的单位法向矢量;下标i,j表示求解域的编号,i,j均为整数,且满足i (7) 对于式(5)中的分界面条件,在分界面处采用双节点并通过罚函数法保证上述所有分界面条件的成立。 1.2 三维温度场控制方程 对于如图1所示的求解域,其温度场控制方程为: (8) 其中,κ,c,ρ,T分别为材料的热传导系数、比热容、质量密度及温升。 对于温度场问题,在Si上的边界条件为: (9) 在Γi,j上 (10) 对于三维涡流场控制方程,采用加权余量法可对控制方程(1)和方程(2)进行离散如下: (11) ∫Ωeσ (12) 式中,Wi,Wi分别为节点i的矢量形状函数和标量形状函数,下标i代表单元内节点的编号。本文研究中采用8节点六面体单元,则i为1~8的整数。 进行单元分析后,可得求解域的离散控制方程为: (13) 式中,K,M,F分别为总体的刚度矩阵、质量矩阵和右端向量,U为节点待求的物理量。 采用欧拉向后差分格式进行时间的离散,式(13)可变为: (14) 式中Δt为时间步长。 类似地,可对三维温度场控制方程进行空间和时间上的离散,得到与式(14)类似的离散控制方程。 在发射过程中,电枢因受到电磁驱动力不断向前加速,假设电枢在每一个时间步长内做匀加速运动,则在Δt的时间内 (15) 式中,Δx为每一时间步下的电枢位移。为保证运动部分与静止部分的网格不发生交错,运动边界两侧的单元在运动方向的尺寸相同,且每一时间步长由式(15)及式(16)确定。 (16) 通过以上离散方法,建立了动态发射下的电磁轨道发射器的三维涡流场有限元模型;结合三维温度场的有限元模型,最终建立了相应的电磁-温度耦合模型。同时,采用运动坐标系处理电枢运动问题可保证最终形成的系数矩阵的正定对称性,在有限元方程数值求解过程中,模型具有无条件稳定性。 为验证所建模型的正确性,以奥卡卢萨电枢测试发射装置(Okaloosa Armature Tester, OAT)发射装置为研究对象[20-21],将模型仿真计算结果与试验编号为SLK 0018的试验结果及EMAP3D仿真结果进行了对比分析。其中OAT发射装置口径为25 mm × 25 mm,试验用的电枢型号为MCA 103,其质量约为249.72 g。 图2为OTA发射装置的四分之一有限元模型。其中空气区域的单元未画出。发射装置的矩形轨道尺寸为31.75 mm × 6.35 mm,轨道与电枢的材料分别为电解韧(Electrolytic Tough Pitch, ETP)铜合金和T7075 铝合金,两种材料电导率的温度特性如图3所示。 图2 轨道及电枢的有限元模型Fig.2 Finite element models of rail and armature 图3 材料电导率的温度特性Fig.3 Thermal properties of material conductivities 在每一时间步长进行计算过程中,模型选择迭代因子w=0.15时,实际的最大迭代次数则为6,具有良好的收敛性。 在仿真过程中,模型与EMAP3D软件采用相同的输入条件。图4为模型计算得出的电流波形与试验电流波形的对比图,图5为模型计算得出的电枢速度曲线与EMAP3D计算值及试验值的对比图。其中,电枢速度的试验拟合曲线是根据试验编号为SLK 0018中的电枢出口速度测量值及试验电流波形,并通过选取合适的轨道电感梯度值推算出的。 由图5可知:当模型采用如图4所示的脉冲电流波形时,电枢侧与轨道侧的实际电流计算值吻合较好。与EMAP3D计算结果相比,有限元模型的电枢速度计算结果与试验测试结果吻合更好。 图4 激励电流试验及仿真波形Fig.4 Current profiles of FEM code and measured value 图5 速度计算值与测试值的对比Fig.5 Comparison of calculated velocity with measured data 如表1、表2所示:在试验过程中,脉冲电流峰值为677 kA,电枢在膛内加速1.0 ms后出口,电枢出口速度为247.0 m/s,出口电流为461.5 kA;模型计算得出的轨道侧峰值电流为676.2 kA,电枢侧峰值电流为669.8 kA,分别比试验值小0.12%和0.11%,计算至1.0 ms时,模型计算得出的轨道侧出口电流为461.8 kA,电枢侧出口电流为465.0 kA,分别比试验值大0.06%和0.76%,电枢末速度计算值约为257.1 m/s,比试验值大4.09%;而EMAP3D程序计算得出的电枢末速度为268.2 m/s,比实验值大8.58%。由此可见:所建模型的数值计算值与试验值吻合较好,间接验证了模型的正确性。 表1 模型的电流计算值与试验值的对比Tab.1 Comparison of calculated currents data with measured data 表2 模型的速度计算值与试验值对比Tab.2 Comparison of calculated velocity data with measured data and EMAP3D’s data 图6与图7分别为动态发射情况下,电枢运动1.0 ms后的轨道及电枢温度云图。由图6可以看出:由于模型并未考虑摩擦热的作用,仅在焦耳热的作用下,由于轨道起始段的通流时间最长,因此,轨道的温度最大值出现在起始段,具体数值约为150 ℃。由图7可知:电枢喉部最高温度约为953 ℃。 图6 t=1.0 ms时,轨道温度云图Fig.6 Temperature contour of rail at t=1.0 ms 图7 t=1.0 ms时,电枢温度云图Fig.7 Temperature contour of armature at t=1.0 ms 图8为电枢加速运动过程中,电磁轨道发射器的电感梯度随时间的变化图,从图中曲线可知:发射器的电感梯度在电流的峰值时刻附近达到最大值,此时的电感梯度大小约为0.46 mH/m,随着时间的推移,电感梯度逐渐减小,在仿真结束时刻,发射器的电感梯度减小至0.42 mH/m。 图8 电感梯度随时间的变化Fig.8 Inductance gradient varies with time 电磁-温度耦合模型可进行电磁轨道发射器动态发射过程的数值模拟。通过模型计算值与EMAP3D程序计算值、试验测试值的对比分析可知:模型的轨道侧及电枢侧电流计算值、电枢出口速度等关键参数均与试验值吻合较好,间接验证了模型的正确性。所开发的有限元程序可为电磁轨道发射器动态发射过程中的磁、热分析及发射器的设计提供一种有效的仿真工具,为轨道烧蚀机理研究提供技术支撑,在一定程度上促进电磁轨道发射技术的发展。同时,其研究成果为电磁发射仿真软件的国产化和未来软件的并行化奠定了理论基础。 References) [1] Hsieh K T, Kim B K. 3D modeling of sliding electrical contact[J]. IEEE Transactions on Magnetics, 1997, 33(1): 237-239. [2] Engel T G, Neri J M, Veracka M J.Characterization of the velocity skin effect in the surface layer of a railgun sliding contact[J]. IEEE Transactions on Magnetics, 2008, 27(7):1837-1844. [3] 王刚华, 谢龙, 王强, 等. 电磁轨道炮电磁力学分析[J].火炮发射与控制学报, 2011, 1(3): 69-71. WANG Ganghua, XIE Long, WANG Qiang, et al. Analysis on electromagnetic mechanics in electromagnetic railgun[J]. Journal of Gun Launch & Control, 2011, 1(3): 69-71. (in Chinese) [4] Liu H P, Lewis M C. 3-D electromagnetic analysis of armatures and rails for high launch energy applications[J]. IEEE Transactions on Magnetics, 2009, 45(1): 322-326. [5] 李昕, 翁春生. 电磁导轨炮固体电枢非稳态电磁效应研究[J]. 南京理工大学学报:自然科学版, 2009, 33(1): 108-111. LI Xin, WENG Chunsheng. Unsteady electromagnetic effect on solid armature railguns[J]. Journal of Nanjing University of Science and Technology: Natural Science, 2009, 33(1): 108-111. (in Chinese) [6] 李昕, 翁春生. 块状固体电枢非稳态电磁效应的三维数值模拟[J]. 弹道学报, 2009, 21(1): 103-106. LI Xin, WENG Chunsheng. Three dimensional numerical simulation of unsteady electromagnetic effect in block solid armature[J]. Journal of Ballistics, 2009, 21(1): 103-106. (in Chinese) [7] Rodger D, Leonard P J, Eastham J F. Modeling electromagnetic rail launchers at speed using 3D finite elements[J].IEEE Transactions on Magnetics, 1991, 27(1): 314-317. [8] Rodger D, Leonard P J. Modeling electromagnetic performance of moving rail gun launchers using finite elements[J]. IEEE Transactions on Magnetics, 1993, 29(1): 496-498. [9] 余海涛, 邵可然, 周克定.迎风-线性棱边单元法[J]. 中国电机工程学报, 1996, 16(2): 92-94. YU Haitao, SHAO Keran, ZHOU Keding. Upwind-linear edge element method[J]. Proceedings of the CSEE, 1996, 16(2): 92-94. (in Chinese) [10] Yu H T, Shao K R, Zhou K D, et al. Upwind-linear edge elements for 3D moving conductor eddy current problems[J].IEEE Transactions on Magnetics, 1996, 32(3): 760-763. [11] Hsieh K T. A lagrangian formulation for mechanically, thermally coupled electromagnetic diffusive processes with moving conductors[J]. IEEE Transactions on Magnetics, 1995, 31(1): 604-609. [12] Hopkins D A, Stefani F, Hsieh K T. Analysis of startup behavior in a “C-Shaped” armature using linked EMAP3D/DYNA3D finite element codes[J]. IEEE Transactions on Magnetics, 1999, 35(1): 59-64. [13] Newill J F, Powell J D, Zielinski A E. Coupled finite element codes for armature design[J]. IEEE Transactions on Magnetics, 2003, 39(1): 148-152. [14] Watt T J, Bryant M D. Cracking and dominant stresses in the throat region of C-shaped solid armatures[J]. IEEE Transactions on Magnetics, 2007, 43(1): 418-421. [15] Watt T J, Bryant M D. Modeling assumptions for railguns[J]. IEEE Transactions on Magnetics, 2007, 43(1): 380-383. [16] Thiagarajan V, Milfeld K, Hsieh K T. Adapting EMAP3D to parallel processing[J]. IEEE Transactions on Magnetics, 2001, 37(1): 143-146. [17] Hsieh K T. Parallelization of EMAP3D based on element-by-element Jacobi preconditioned conjugate gradient method[J]. IEEE Transactions on Magnetics, 2003, 39(1): 139-147. [18] Vanicek H, Satapathy S. Thermal characteristics of a laboratory electromagnetic launcher[J]. IEEE Transactions on Magnetics, 2005, 41(1): 251-255. [19] 谢德馨, 杨仕友. 工程电磁场数值分析与综合[M]. 北京: 机械工业出版社, 2009. XIE Dexin,YANG Shiyou. Electromagnetic field numerical analysis and synthesis of engineering[M]. Beijing : China Machine Press, 2009. (in Chinese) [20] Price J H, Yun H D. Design and testing of integrated metal armature sabots for launch of armor penetrating projectiles from electric guns[J]. IEEE Transactions on Magnetics, 1995, 33(1): 219-224. [21] Hsieh K T, Kim B K. International railgun modeling effort[J]. Transactions on Magnetics, 1997, 33(1): 245-248. Numerical simulation of dynamic launching in electromagnetic rail launcher TAN Sai, LU Junyong, ZHANG Xiao, LONG Xinlin (National Key Laboratory of Science and Technology on Vessel Integrated Power System,Naval University of Engineering, Wuhan 430033, China) For the numerical simulation method of the dynamic launching in electromagnetic rail launcher, a discrete formulation of three dimensional transient eddy problem for electromagnetic rail launcher considering dynamic launching was established, based on the magnetic vectorAand the time integrated electrical scalar potentialV, combined by using nodal element method and the moving coordinate frame to deal with the motion. The corresponding three dimensional magnetic-thermal coupled model was formed finally by using the governing equation for thermal field. The dynamic launching process of an electromagnetic rail launcher was simulated by the finite element model. Numerical analysis results of FEM (finite element method) code and the experiment results were compared and analyzed. The characteristic of thermal field distribution for launcher and the variation of inductance gradient with time were obtained by the model. Results show that the magnitudes of the pulsed current, muzzle current, and muzzle velocity have good correspondence with measure dates respectively, which has verified the correctness of the FEM code. dynamic launching; armature; electromagnetic rail launcher; inductance gradient; finite element method 10.11887/j.cn.201606007 2016-03-29 国家自然科学基金资助项目(51207162,51522706);国家部委基金资助项目(613262) 谭赛(1988—),男,河南永城人,博士研究生,E-mail:tansai208@126.com; 鲁军勇(通信作者),男,教授,博士,博士生导师,E-mail:ljy041@sohu.com TM315 A 1001-2486(2016)06-043-06 http://journal.nudt.edu.cn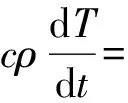
2 有限元离散方程

3 模型验证与分析



4 结论
