运动目标追踪的人工鱼群优化粒子滤波算法

张婷婷，于 明，阎 刚

（河北工业大学 天津市电子材料与器件重点实验室，天津 300130）

运动目标追踪的人工鱼群优化粒子滤波算法

张婷婷，于 明，阎 刚

（河北工业大学 天津市电子材料与器件重点实验室，天津 300130）

为了进一步提高视频图像序列中的运动目标追踪精度，在扩展卡尔曼粒子滤波中引入人工鱼群算法，利用人工鱼群算法优化采样过程，使粒子不断朝高似然区域移动来寻找最优位置；然后对重采样过程优化，提高样本多样性，克服粒子样本贫化问题，提高对系统状态的预估精度；最后以颜色直方图特征描述运动目标，结合目标的运动特征建立游走模式的二阶自回归模型，以提高运动估计精度．对比标准粒子滤波（PF）、扩展卡尔曼粒子滤波（EKPF），人工鱼群优化扩展卡尔曼粒子滤波算法（AFSA-EKPF）能够将滤波结果均方误差的均值和方差分别降低至0.113 86和0.003 09，同时在追踪运动目标实验中，能够有效地消除目标遮挡所带来的影响．

运动目标跟踪；扩展卡尔曼粒子滤波；人工鱼群；颜色直方图

0 引言

有效的目标跟踪系统要求较高的实时性、鲁棒性，但在实际环境中，运动目标姿态、遮挡、形变、背景及光照等因素对跟踪过程的鲁棒性会产生一定的影响，有效解决复杂环境条件下的运动目标状态估计问题是目标跟踪领域的一个难点[1]．近些年来，基于MonteCarlo方法和递推Bayesian估计的粒子滤波算法成为解决非线性、非高斯条件下系统估计问题的有效方法，不同于传统的卡尔曼滤波方法，粒子滤波直接将非线性的系统模型进行非线性变换，采用的随机样本方法对系统状态的概率分布描述，使得非线性状态估计更接近随机系统的非线性本质[2]．

有研究者将粒子滤波应用于目标跟踪，以解决其中的非线性、非高斯问题[3]．广泛使用的序列重要性采样（SIS）会带来粒子退化问题，N.J.Gordon等人提出了在SIS粒子滤波算法后进行重采样，来减缓粒子退化的问题，但是又带来了粒子贫化问题——重采样后丧失粒子多样性，具有较大权值的粒子被多次选取，经过若干次迭代后，所有的粒子都集中在一个点上[4]．

近年来学者们提出了很多改进方法[4-6]，与传统的解决方法不同，一些学者通过智能优化算法来避免粒子贫化问题[7-8]，Kotecha和Djuric提出高斯和粒子滤波（GSPF）算法，考虑到系统模型比较复杂时，单一高斯分布近似后验分布远远不够，结合高斯滤波和粒子滤波的优点，不需要重采样步骤，算法避免了贫化问题且精度有所提高．Cai[9]等人提出了人工鱼群优化粒子滤波算法，利用人工鱼群算法优化粒子运动，使其朝高似然区域移动，从而提高状态估计精度．但这种算法没有考虑最新的观测数据，采样得到的粒子集不能有效地表示后验概率．

为了进一步解决粒子退化和贫化带来的滤波精度降低问题，本文研究提出一种新的算法 AFSA-EKPF （ArtificialFish-Extended Kalman Particle Filtering），将人工鱼群算法引入到扩展卡尔曼粒子滤波中，分别优化采样过程和重采样过程，调节似然函数使粒子集不断向真实状态值移动，解决粒子退化和贫化问题，提高滤波精度，并且以颜色特征描述运动目标，对比标准粒子滤波（PF）、扩展卡尔曼粒子滤波（EKPF），分析实验结果．

1 扩展卡尔曼粒子滤波

扩展卡尔曼粒子滤波算法的基本思想是利用扩展卡尔曼滤波（EKF）来构造粒子滤波的建议分布函数，从重要性密度函数的角度对粒子滤波算法进行改进[10]．

EKF通过高斯近似更新后验分布来实现递推估计，融合最新的观测值，在每时刻按照公式(1)对后验密度进行近似

EKPF应用EKF方法可以得到一个相对较好的重要性密度函数，但粒子权重的方差随时间而递增，使得只有少量的粒子具有较大权值，粒子的权重集中到少量粒子上，因此大量的工作都被浪费在小权值粒子上．同时重采样过程中出现了粒子样本贫化问题，经过几次迭代以后大权值的粒子被选择多次，导致粒子集的多样性降低，不能有效的表示后验概率密度，存在一定的退化现象．尤其是当似然函数非常窄或似然函数位于先验概率分布尾部时，粒子样本贫化问题更加严重，如图1、图2所示，在这些情况下会出现很大的模型误差，从而导致滤波精度下降．

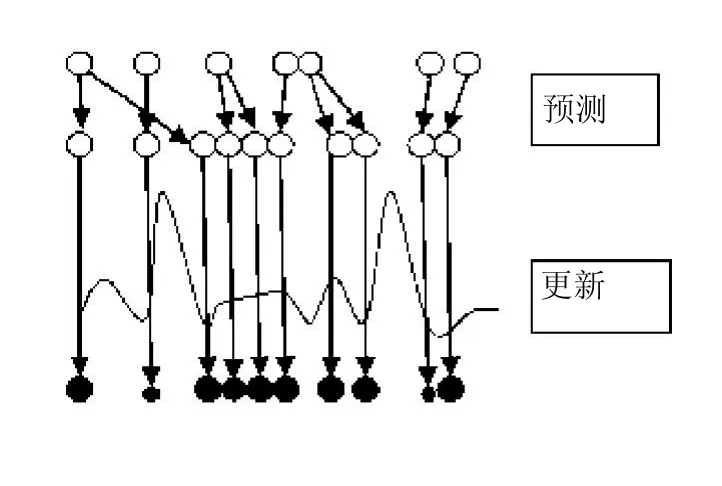
图1 窄的似然函数Fig.1 Situation of narrow likelihood function

图2 似然函数位于先验概率分布尾部Fig.2 Likelihood function located in the tailof prioriprobability

2 人工鱼群算法

人工鱼群算法是一种基于鱼群自治体的寻优策略．在水中鱼类数量最大的地方往往是该水域营养最丰富的地方，所以通过模拟鱼群的行为来寻找全局最优．鱼群一般具有3种自由行为：觅食、追尾和聚群．觅食行为是指每条鱼在自由游动情况下，发现食物时，都会朝着食物多的方向游去．追尾行为是指在鱼群中某些个体发现前方有食物时，相邻个体会追随其朝食物所在地点游去．聚群行为是为了保证自身种群生存而养成的一种生活习性，鱼在水中自由移动时都会聚集成群．其中鱼群中个体的觅食行为可以达到局部最优，而追尾和聚群行为可以跳出局部最优使鱼群达到全局最优．

根据上述情况，使每条人工鱼根据自身以及四周的情况自由选择一种行为．最后人工鱼将停留在局部极值周围，在实际应用中求极大问题时，目标函数值最大的人工鱼一般停留在值最大的极值域周围，因此可根据该内容找出全局极值域．同时一般情况下值最大的极值域周围会停留着最多的人工鱼，可根据这一特性找到全局极值．鱼群的觅食行为可以获取到局部极值，追尾和聚群行为都是帮助跳出局部极值从而获取到全局极值点．人工鱼群算法对追尾和聚群行为进行评价，然后选择一种合适的行为，最终快速高效地达到全局最优[]．

3 基于人工鱼群优化的扩展卡尔曼粒子滤波算法

将人工鱼群算法引入到扩展卡尔曼粒子滤波算法中，把粒子当作人工鱼，鱼群通过不断更新自己的位置来随机寻找高食物浓度的区域，把似然度当作食物浓度，当人工鱼没有发现相对自身较高的浓度区域时，他们会不断地随机游动直到搜索到高浓度区域．再优化采样过程和重采样过程，使粒子集通过似然函数调节不断向真实状态值移动．

通过人工鱼群算法优化觅食和聚群行为，粒子集不断向系统中最优粒子靠近，智能粒子集群则向高似然区域移动，如图3所示，从而解决粒子退化和贫化问题，可以提高滤波精度．对动态系统进行一阶线性化近似，缩小与真实后验分布产生样本的偏差．当迭代次数达到设定上限或人工鱼群的最优值符合某阈值时，表明人工鱼群已经分布在真实状态附近，则停止优化．此时再利用最新观测值对粒子集进行权重更新并做归一化处理．

图3 人工鱼群优化过程Fig.3 Processof artificial fish schoolalgorithm optimization

基于人工鱼群优化的扩展卡尔曼粒子滤波算法（AFSA-EKPF）：

Step2：用EKF方法更新每时刻的采样粒子，更新公式为公式 (3)

Step3：从重要性密度函数中采样并计算权值，更新公式为公式 (4)、公式 (5)

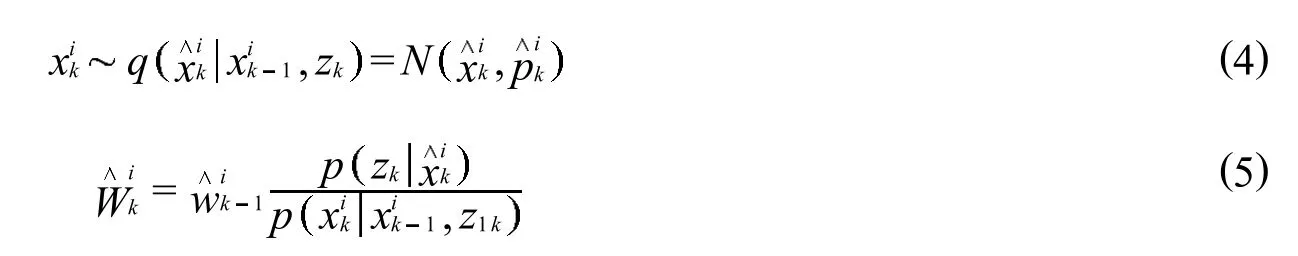
Step4：利用人工鱼群算法优化，只考虑鱼群的觅食和聚群2种行为时，所采用的目标函数为公式 (6)．

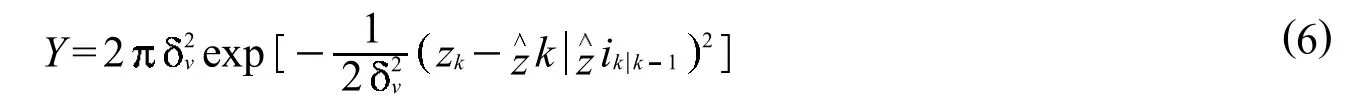
对觅食行为和聚群行为进行建模寻找局部最优，设定阈值和迭代上限，当目标函数的偏差小于某阀值，或者迭代次数达到设定上限时终止算法．

Step5：归一化并更新粒子权值，更新公式为公式 (7)

Step8：当k=k+1时，跳转至Step2．

通过人工鱼群算法优化粒子集，使粒子集不断向高似然区域移动，增加粒子样本集的多样性，缓解粒子的退化现象并解决粒子贫化问题，最终得到的粒子集可以充分表示粒子的真实分布状态，保证权值最大的粒子用于估计，从而有效改善因粒子退化和贫化而造成的滤波精度下降问题．

4 实验结果分析

为了验证本文算法的有效性，首先对比了标准粒子滤波（PF）、扩展卡尔曼粒子滤波（EKPF）、人工鱼群优化扩展卡尔曼粒子滤波算法（AFSA-EKPF）的滤波实验，然后将粒子滤波应用于目标跟踪，对比分析了运动目标遮挡下的目标追踪实验．

4.1 粒子滤波实验及分析

进行人工鱼群优化扩展卡尔曼粒子滤波算法（AFSA-EKPF）仿真实验，并与标准粒子滤波（PF）、扩展卡尔曼粒子滤波（EKPF）进行对比分析，系统模型如公式 (8)、公式 (9)

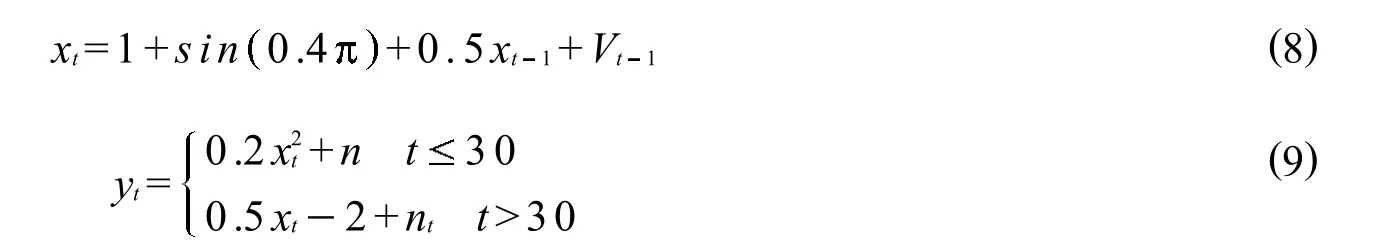
式中：Vt1～Gamma 3,2为过程噪声，Nt～0,0.00001，粒子数N=100，观测时间T=60；感知距离visual= 0.3，人工鱼群算法中的步长step=0.15，实验中采用均值估计系统的状态，即进行了100次独立实验．

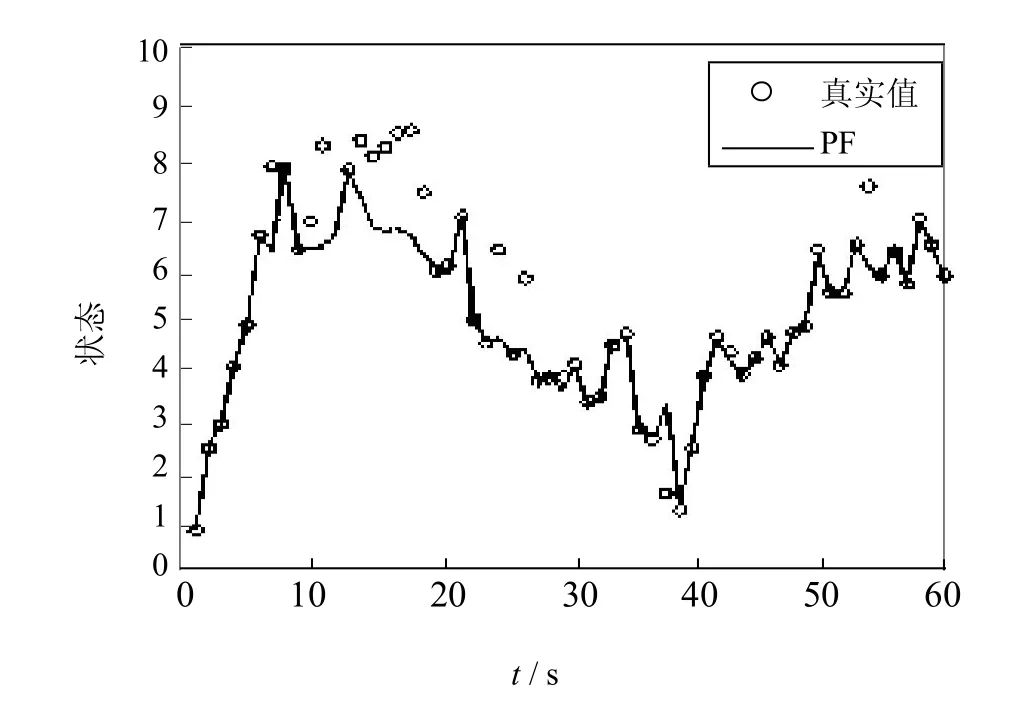
图4 PF的状态估计曲线Fig.4 Stateestimation curveof PF

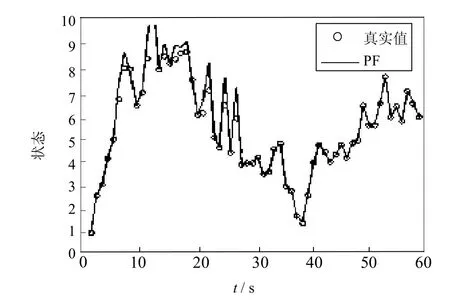
图5 EKPF的状态估计曲线Fig.5 Stateestimation curveof EKPF

图4，图5，图6分别是PF、EKPF和AFSA-EKPF的状态估计曲线，图7为一次独立实验条件下的3种算法的状态估计曲线，图8为3种算法进行100次独立实验的均方误差曲线，表1为3种算法进行100次独立实验的均方误差均值和方差．

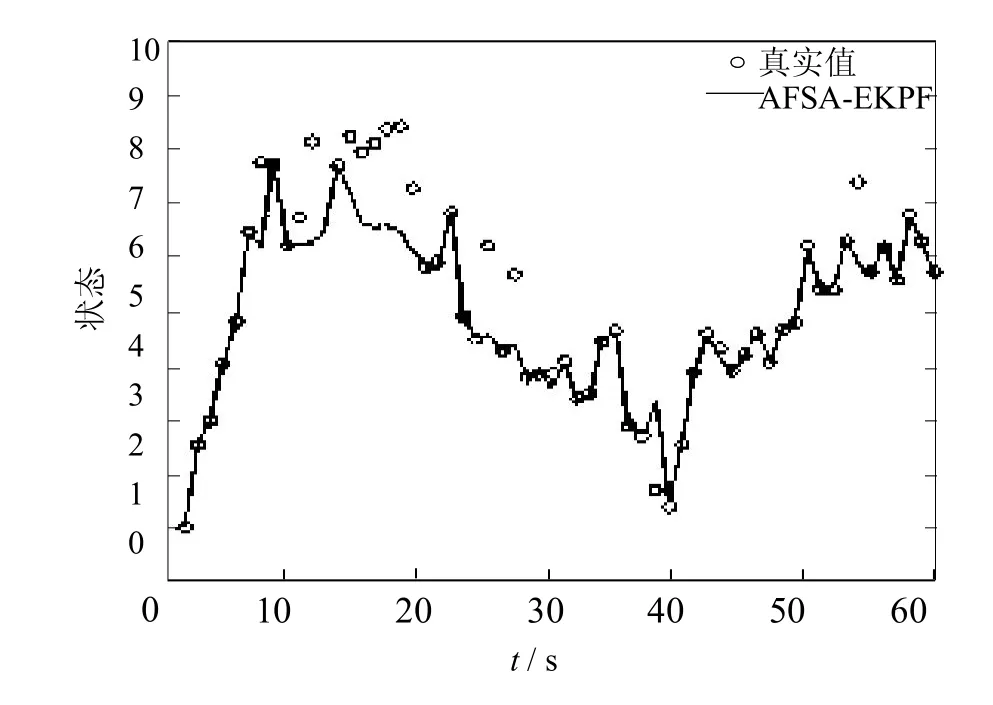
图6 AFSA-EKPF的状态估计曲线Fig.6 Stateestimation curveof AFSA-EKPF

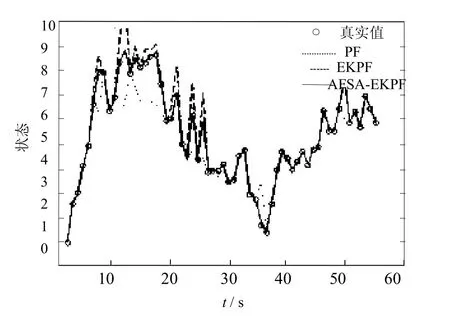
图7 PF、EKPF和AFSA-EKPF的状态估计曲线Fig.7 Stateestimation curveof PF,EKPFand AFSA-EKPF

图7是3种算法的状态估计曲线，由实验结果可以看出本文提出的AFSA-EKPF的曲线相似程度更高，其估计值更接近于真实值，从而可以提高滤波效果．由图8中3种算法的均方误差（MSE）曲线的比较可以看出，AFSA-EKPF算法的均方误差值最低．表1中数据为100次独立实验中3种算法的均方误差的均值和方差，通过对比AFSA-EKPF的值明显小于PF和EKPF算法，说明本文算法提高了对系统状态的预估精度．综上所述本文算法优于PF和EKPF算法，滤波精度更高，解决了由于粒子退化和贫化导致的滤波精度降低问题．

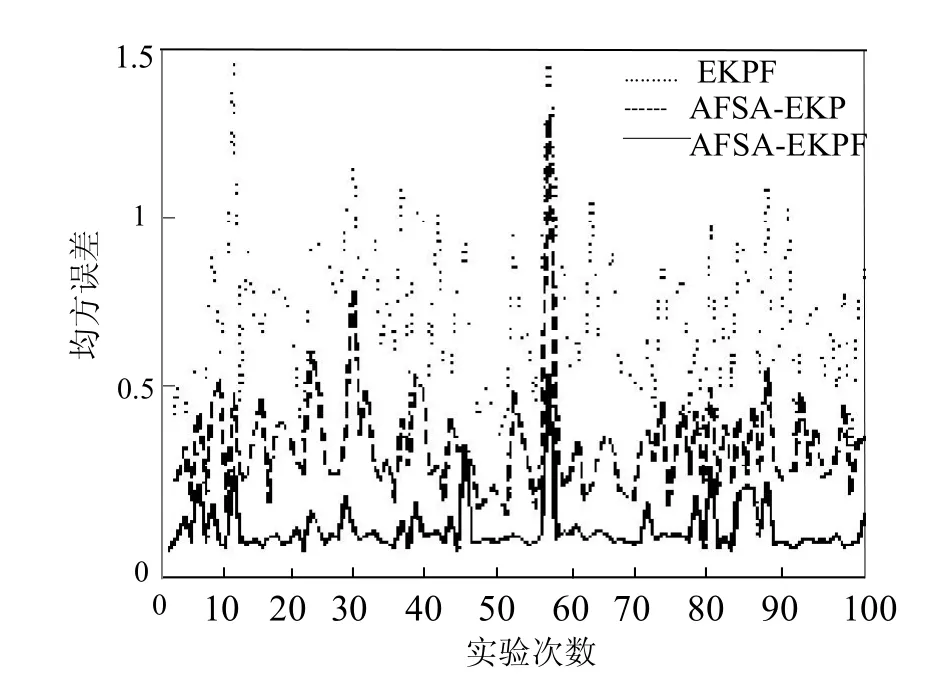
图8 PF、EKPF和AFSA-EKPF的均方误差曲线Fig.8 Mean Squared Error curveof PF,EKPFand AFSA-EKP

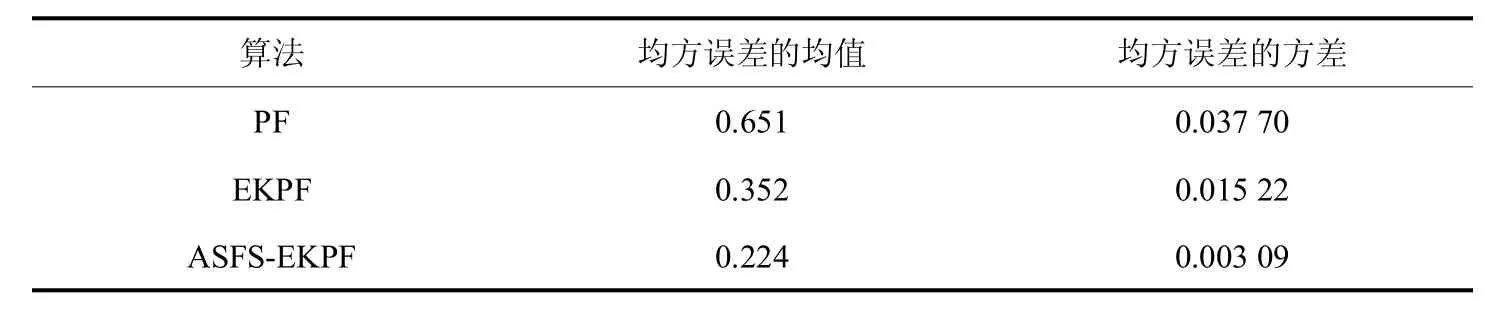
表1 PF、EKPF和AFSA-EKPF均方误差的均值和方差Tab.1 Mean and variance ofMSE aboutPF，EKPFand AFSA-EKPF

4.2 目标跟踪实验

颜色特征是每个物体最本质的物理特征，同时也是人类认识世界，感知世界和区分物体的一种主要辨认特征．用颜色特征描述目标，当目标进行平移、部分被遮挡以及旋转时都能保持稳定，具有较强的鲁棒性．颜色直方图将颜色空间分为若干个小的颜色区间，整个过程叫做颜色量化（color quantization），每个小的区间称为颜色直方图的一个柄，最终统计各个区间内的像素数量，颜色直方图统计了一副图像中颜色的数量特征，计算了不同色彩在整幅图像中所占的比例．该方法不用考虑像素所在的空间位置，简单、快速、易于实现，这里选取颜色直方图提取目标的颜色特征．区域y上的颜色直方图的构建方法可表示为公式 (10)

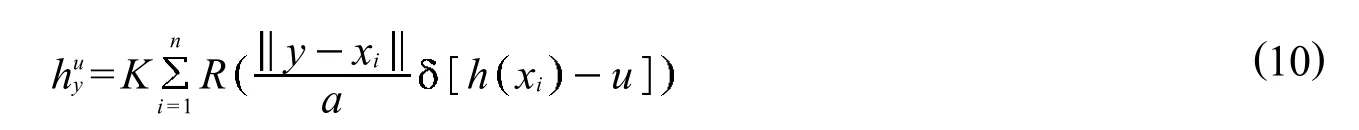
其中：K为归一化常数； 为Kroneckerdelta函数．

实验在奔腾4处理器，2.93 GHz主频、512M内存的台式PC机上进行，采用MATLAB 7.1软件平台实现的．视频来自视频数据库[12]，视频实验中所采用的图像序列总长80帧，图像分辨率128×96，帧率24 fps．实验中手动选取第一帧图像中的目标初始化为模板，粒子数设为100，重采样预支阀值设为0.9．视频1是一个人在行走过程中人脸被另外一个人遮挡的情况．人在走动时由于遮挡使得人脸部的外观模型发生了较大变化，并且两个目标颜色相似，因此使得稳定的跟踪目标比较困难．从图9a）可看出在目标未被遮挡前标准的粒子滤波算法可以稳定的跟踪目标，但是由于重采样，而造成粒子多样性降低，在26帧到30帧中被颜色相似的另外一个目标遮挡时跟踪效果失败．从图9b）中可以看出本文提出的算法在整个目标运动中都能较为准确的跟踪目标，由于增加了粒子样本的多样性，每一个粒子就代表一种状态信息，即增加了目标状态的多样性，粒子越丰富，算法估计能力越强，从而在目标的运动状态发生变化（被遮挡）的情况下也具有较好的效果．

图9 视频1跟踪结果Fig.9 Tracking resultsof the Video 1

图10 视频2跟踪结果Fig.10 Tracking resultsof the Video 2

视频2是人在走动时被另外一个目标遮挡的情况．从图10a）可看出在行人在未被遮挡前标准的粒子滤波算法可以稳定的跟踪目标，但是在17到19帧中被遮挡时跟踪效果失败．从图10b）中可以看出本文提出的算法在整个目标运动中都能准确的跟踪目标，由于改善了粒子分布情况，增加了目标状态的多样性，从而在目标的运动状态发生变化（被遮挡）的情况下也具有较好的效果．

5 结论

本文提出一种运动目标追踪的人工鱼群优化扩展卡尔曼粒子滤波算法，将人工鱼群算法引入到扩展卡尔曼粒子滤波中，有效地防止粒子退化和贫化问题，提高对系统状态的预估精度，更适合在对精度要求高的系统中进行滤波计算．以颜色特征描述运动目标，结合目标的运动特征建立了游走模型的二阶自回归模型，提高了运动估计精度．大量的实验证明，本文的算法可以提高跟踪的准确性，尤其是当目标被遮挡时跟踪效果良好．

[1]Zhang Sh J，Stentiford F．Motiondetectionusingamodelofvisualattention[C]//Proceedingsof IEEE InternationalConferenceon ImageProcessing，2007，1：513-516．

[2]CappeO，GodsillSJ，Moulines E．An overview ofexistingmethodsand recentadvances in sequentialMonte Carlo[J]．Proceedingsof the IEEE，2007，95（5）899-924．

[3]Boers Y，Driessen JN．Inter-actingmultiplemodelparticle filter[J]．IEEEProceedingsof Radar Sonar Navigation，2003，150（5）：344-349．

[4]韩磊，郭晓金，齐威，等．改进的粒子滤波算法 [J]．电视技术，2012，36（7）：16-19．

[5]Cheng Yongming，JiangM ingyan，Yuan Dongfeng．Novelclusteringalgorithmsbasedon Improved artificial fish swarm algorithm[C]//Proceedings of Sixth InternationalConferenceon Fuzzy Systemsand Know ledge Discovery，2009，3：141-145

[6]Han H，Ding Y S，Hao K R．An evolutionary particle filterw ith the immunegenetic algorithm for intelligentvideo targettracking[J]．Computers &Mathematicsw ith Applications，2011，62（7）：2658-2695．

[7]Musso C，Oudjane N，Legland F，Improving regularized particle filters[D]．SequentialMonte Carlo Methods in Practice，New York：Springer-Verlag，2001．

[8]PARK S，HWANG JP，KIM E．A new evolutionary particle filter for thepreventionofsample improverishment[J]．IEEETransEvolutionary Computation，2009，13（4）：8010-809．

[9]CaiY．Artificial fish schoolalgorithm applied inacombinatorialoptimizationproblem[J]．International Journal of IntelligentSystemsand Applications，2010，2（1）：37-45．

[10]LiLiang-qun，JiHong-bing，Luo Jun-hui．The iterated extended Kalmanparticle filter[C]．Proceedingof IEEE InternationalSymposium on Communicationsand Information Technology，2005：1213-1216．

[11]Yongm ing Cheng，M ingyan Jiang，Dongfeng Yuan．Novelclusteringalgorithmsbased on improved artificial fish swarm algorithm[C]//Proceedings of Sixth InternationalConferenceon Fuzzy Systemsand Know ledge Discovery，2009，3：141-145．

[12]http：//www．ces．clemson．edu/tb/research/headtracker/seq/．Accessed 21Sept2012．

[责任编辑 代俊秋]

Moving object tracking based on artificial fish particle filtering

ZHANG Tingting，YUM ing，YAN Gang

(Tianjin Key Laboratory of Electronic Materialsand Devices,HebeiUniversity of Technology,Tianjin 300130,China)

In order to improve the precision ofmoving object tracking in video image sequence,artificial fish algorithm is induced into extended Kalman particle filtering.The sampling process isoptim ized by artificial fish algorithm to find theoptimalposition bymaking the particlemoving towards thehighly likelihood region.Then re-sampling process isoptim ized to improvevariety ofparticle,and overcome thedilution ofparticle to improveestimated accuracy ofsystem state. Finally,two-orderautoregressivemodel is constructed to improve the precision ofmoving object tracking by colorhistogram feature.Comparingw ith the standard particle filtering and extended Kalman particle filtering,experimental results based on artificial fish-extended Kalman particle filtering can produce highter precision,Mean and variance of MSE are reduced to 0.113 86 and 0.003 09 respectively.Influenceof Targetocclusion is reduced while tracking themoving object extremely.

moving object tracking;extended kalman particle filtering;artificial fish;colorhistogram

TP391.41

A

1007-2373(2016)04-0012-08

10.14081/j.cnki.hgdxb.2016.04.003

2015-11-17

河北省自然科学基金（F2015202239）；天津市科技计划项目（15ZCZDNC00130）

张婷婷（1984-），女（汉族），讲师，博士生．