ax=by=cz问题的求解

重庆市巫山中学2017级39班 易晓红

ax=by=cz问题的求解

重庆市巫山中学2017级39班 易晓红

对数是同学们进入高中数学学习后接触的一类新的代数运算，就因为其运算符号的特殊性及相关字母的限制条件，使得很多同学总是望而生畏。要将对数运算作为工具运用于解题过程中，还得先了解其运算的优越性。

由于对数的运算性质知，对数运算可将积、商、乘方的运算转化为和、差、等运算，因此对数运算可以起到降次及降低运算级别的作用，由此联想到指数间的运算可由对数运算进行转化。

下面就指数式中的一类题型加以探讨：

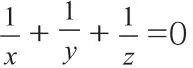
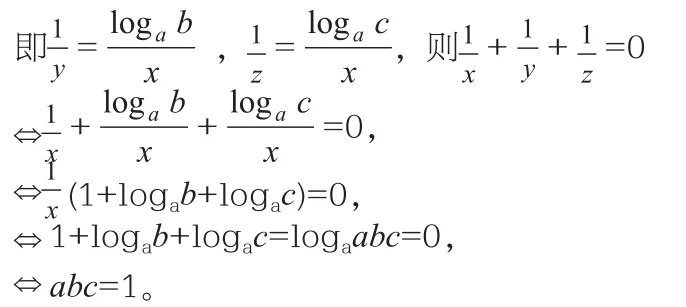
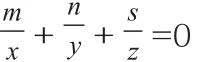
下面来看定理的应用：例1 已知：2x=3y=12z，求x、y、z满足的一个关系式。

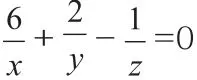
例3 已知，a、b、c为不等于1的正实数，x、y、z为非零实数，ax=by=cz，且xy+2yz-3xz=0，求证2lga-3lgb+lgc=0。

解：∵x、y、z为非零实数，且xy+2yz-3xz=0，

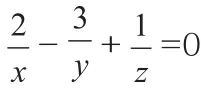
由 推 论 知：a2b-3c=1， 两 边 同 取 常 用 对 数 得：2lga-3lgb+lgc=0。

小结：若a、b、c为不等于1的正实数，x、y、z为非零实数，且ax=by=cz，则mxy+nyz+sxz=0的充要条件为nlga+slgb+mlgc=0。