基于运行概率特征的电力储能系统测试工况设计方法

白恺

(国网冀北电力有限公司电力科学研究院，北京市 100045)

基于运行概率特征的电力储能系统测试工况设计方法

白恺

(国网冀北电力有限公司电力科学研究院，北京市 100045)

目前国内已投运大容量储能电站使用的电池大多数为电动汽车电池生产线所生产的产品，测试其产品性能的方法多为标准工况或电动汽车行驶工况。分析某大容量储能电站各种控制模式下历史运行数据，提出一种大容量储能电站典型测试工况的设计方法，以电流幅值分布、电流变化率及充放电转换次数作为特征值，综合考虑重复周期内能量转移代数和为0。算例中1 h典型测试工况与真实运行工况特征值概率分布总误差小于2%，实现了基于典型测试工况的锂电池模组性能衰减实验室测试，为研究储能电站电池选型和性能评估提供了技术手段。

储能系统；概率分布；典型工况；性能衰减

0 引 言

近年，随着风、光等新能源发电技术的应用，电力储能市场一直保持较快增长。据中关村储能产业技术联盟CNESA项目库不完全统计，截至2015年底全球储能在电力系统的累计装机总量为946.8 MW(不包含抽蓄，压缩空气储能及储热)。2015年中国累计运行储能项目118个，累计装机规模105.5 MW[1]。但国内大容量储能在电力系统中的应用起步于2012年，目前已积累了一定的运行数据，有必要对现有运行数据进行充分研究和分析，为储能技术在电力行业的应用提供更多技术支撑。

储能电池、电池组的老化受多重因素影响，包括充放电工作模式、电流大小，运行环境的温度、压力，电池制作工艺、本身结构及化学特性等[2-3]。目前已有的电池性能测试一般基于标准工况或设定工况，标准工况是指一定条件下的满充满放循环工况，在标准工况下测试所得的电池寿命为循环寿命。设定工况的相关研究成果集中于对于不同的车型和动力系统配置、不同路况和行驶路径来设置电池的工况[4]。目前应用较为普遍的测试工况[5]如《美国先进电池联合会(USABC)电动汽车电池试验手册》是USABC对美国联邦城市汽车运行工况进行简化后，得到的动态应力测试工况(dynamic stress test，DST)；我国轻型车一般采用的测试循环是欧洲的行驶工况ECE15+EUDC[6]。文献[7]提出了基于实车运行数据的动力电池动态测试工况统计方法, 应用该方法建立了基于北京公交的纯电动客车用动力电池动态测试工况，并对工况进行了标准化，提出该工况应用于不同车型和不同电池组的等价方法。文献[8]基于纯电动公交车采集的运行数据，提出了一种分析动力电池行驶循环特征的方法，分析公交车行驶过程中的功率分布情况，利用主成分分析方法验证测试工况与样本总体的主要特征量之间的相关性，分别采用恒流恒压、标准动态应力测试和纯电动公交动态测试工况进行锰酸锂电池的寿命试验。文献[9]提出基于中国典型城市循环工况的动力电池非恒流放电测试方法，为电动汽车用动力电池的选型及性能匹配测试提供参考。文献[10]提出了一种基于GPRS的道路行驶工况数据的远程采集方法，从而获得电动汽车道路试验原始数据库，同时将自组织映射神经网络引入到行驶工况的自学习中，通过网络对原始数据进行运动学片段的聚类分析，构建出了电动汽车在实际运行中的3种典型工况。

上述文献均依据不同种类电动汽车的行驶特点和路况特点，结合数学方法，得出电动汽车电池的典型运行工况。目前还没有文献对我国电力储能的典型工况进行研究。

储能在电力系统中的应用模式较多，即使在相同控制模式下，也因应用环境、容量配比和控制参数等不同，运行工况需求也会有所差异。提取储能电池模组典型测试工况，提供与实际运行工况类似的设定工况，一方面可在电站设计阶段，为电池的选型、性能匹配提供参考；另一方面也可对已投运系统开展模组寿命衰退分析。本文以某储能电站运行数据为基础，分析电力储能工况特征，提出基于特征值概率分布与误差分析的储能系统典型测试工况设计方法。

1 电力储能运行工况特征分析

大容量电力储能目前常用的运行模式有平滑风光的波动性、移峰填谷、跟踪发电计划及调频等[11]。平滑波动工况一般依据预期的平滑度指标，通过控制储能系统对有功功率的吞吐[12]，实现储能系统对风光功率的多时间尺度平滑处理[13]，使得总输出功率波动在规定范围内。跟踪计划发电工况是指通过协调储能发电系统，对风光发电出力与发电计划值之间的偏差进行实时补偿，使得全站发电依据计划值输出，得到满意的计划跟踪效果[14]。削峰填谷一般基于峰谷电价差对风光有功出力进行调整，提高经济效益[15]。储能系统参与电网调频是指充分发挥储能响应快速，跟踪精准的优势，由储能参与区域控制偏差(area control error，ACE)跟踪，从而改善由于传统机组响应慢、爬坡速率低造成的电网调频性能不佳的问题[16]。

为了提取上述工况的特征量，对位于张家口的国家风光储示范电站储能系统2013年运行数据进行分析。截取2013年储能电站在4种工况下的出力曲线，绘制日典型工况，并对比各种工况出力特性如图1所示。调频工况下，储能系统大多数情况下出力较小，波动率较小，充放电转换较少；削峰填谷工况下，储能系统基本以恒定功率充放，充放电转换较少；跟踪计划发电工况下，储能系统出力总功率大，波动率大，充放电转换相比其他工况更为频繁；平滑风光波动工况下，储能系统出力波动率较大，出力较小。

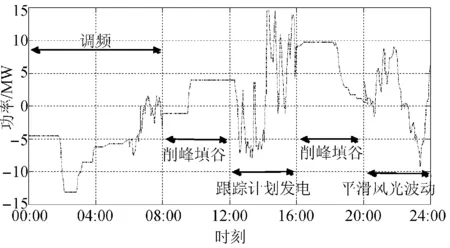
图1 储能电站典型工况曲线示意图Fig.1 Typical operating condition curve of energy storage power station

由于通常储能厂房或集装箱内有较为完备的温度控制系统，电池工作温度恒定在20 ℃左右，可忽略温度对电池的影响，且电池密封在电池箱内，处于静止状态，应力的变化可忽略。要表达运行工况所有信息量，则至少需要4个特征量：充放电电流曲线幅值分布、电流变化率分布、充放电转换次数及储能系统出力为0的概率分布。

2 电力储能运行典型工况设计方法

2.1 典型工况的设计目标

为了研究大容量储能系统运行工况下电池模组性能衰减规律，需设计用于实验室测试的典型工况。典型工况应满足以下要求：(1)涵盖大容量储能系统运行工况的重要特征，逼近真实运行数据；(2)典型工况循环时间周期较短，便于试验人员暂停试验与试验数据分析；(3)1个循环周期内，电池模组的能量转移代数和接近于0，即荷电状态(state of charge，SOC)回到起始点，以减少试验过程中对SOC的调整。

2.2 典型工况设计方法

如图2所示，典型工况设计步骤如下。

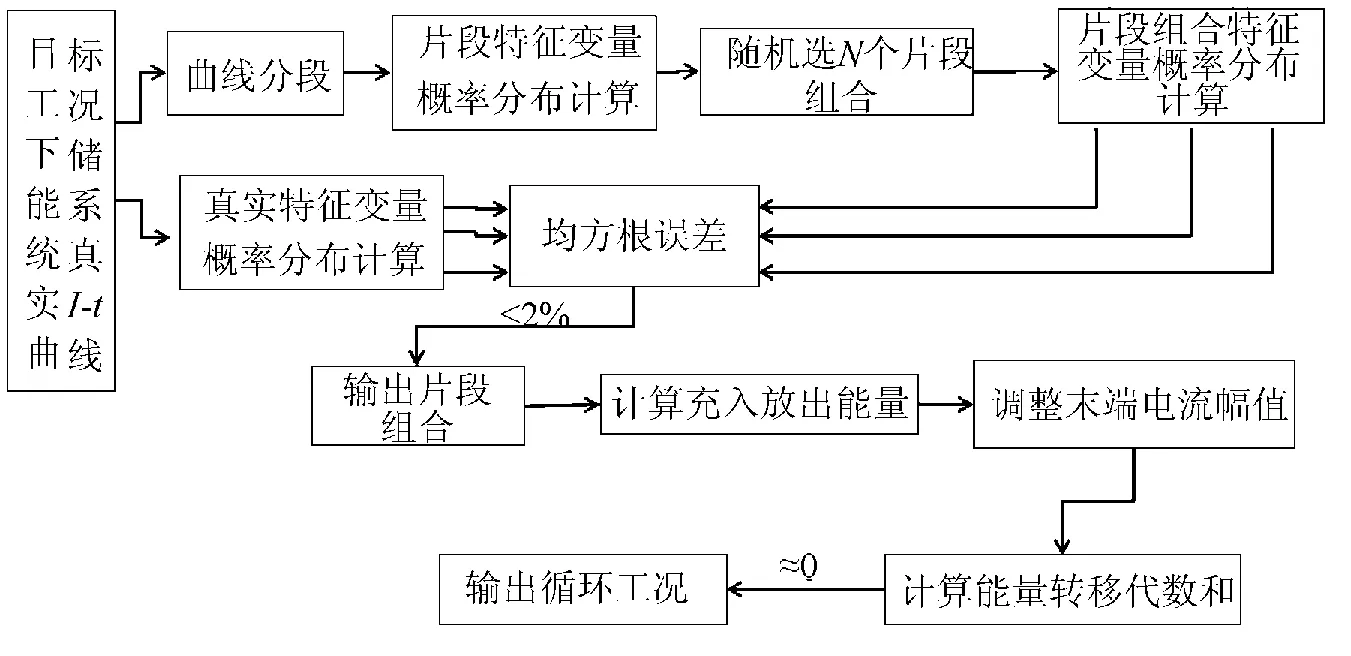
图2 典型工况设计步骤Fig.2 Design steps of typical operating condition

步骤(1)：获取历史运行数据。充放电电流可以表征储能系统出力的大小，获取长周期电流和时间数据作为主要分析对象。其中应剔除储能系统检修维护等停机原因导致储能出力为0的片段。

步骤(2)：计算历史运行数据特征量分布。计算历史运行曲线每一点的电流幅值、电流变化率及设计工况内的充放电转换次数。电流幅值即每一点的电流大小It，充电为负、放电为正。电流变化率It计算方法如式(1)，其中T为历史运行数据中电流的采集周期，一般为s级。

(1)

充放电转换次数为设计工况内电流由正转为负、由负转为正的次数。

步骤(3)：将电流幅值、电流变化率分段(分段越密集，典型工况曲线越精确，但计算量越大)，统计落在每一段中的时间点个数占总点数的百分比，电流幅值概率分布统计结果记为矩阵A、电流变化率概率分布统计结果记为矩阵B、充放电转换次数统计结果记为矩阵C。

步骤(4)：依据试验条件首先设定所需设计工况长度Tc,小片段长度TCN的确定需综合考虑精度和计算量，并与Tc成整数倍关系。Tc与TCN的比值为设计工况内小片段个数N。

步骤(5)：计算小分段曲线特征量概率分布。计算每一个小片段内，每一点的电流幅值、电流变化率、设计工况内的充放电转换次数和出力为0的次数。

步骤(6)：随机选取N个小片段组合为一个长度为Tc的新曲线，计算该曲线的特征量概率分布，并按照步骤(3)中设置的分段区间，统计落在每一段中的时间点个数占总点数的百分比，电流幅值概率分布统计结果记为矩阵A′、电流变化率概率分布统计结果记为矩阵B′、充放电转换次数统计结果记为矩阵C′。

步骤(7)：误差计算。计算历史运行曲线与设计工况曲线每一个特征量在每一段概率分布中的误差，如式(2)—(4)：

(2)

(3)

C-C′=c

(4)

电流幅值误差eA，电流变化率误差eB，充放电转换次数误差eC分别如式(5)—(7)：

(5)

(6)

eC=c

(7)

总误差e为

(8)

步骤(8)：调整终点SOC。输出满足总误差要求(一般推荐小于2%)的片段组合，组成的新曲线记为I1。计算I1的充入和放出电量，考虑到典型工况的可连续循环性，每次循环后SOC应能够回到原点。由于在电流幅值分布中，一些接近峰值的电流值占比很小，但对电池寿命的影响较大，将充入和放出电量的差，用电流幅值较大值进行短时充放，使SOC回到原点。

步骤(9)：校验误差，输出典型工况I2-t曲线。

3 电力储能运行典型工况设计算例

选取某储能单元连续3天运行于平滑波动模式下的电流时间曲线，剔除出于安全考虑的夜间停机时间和故障检修时间，共约36 h。该单元由1台变流器和10组电池组组成，直流侧额定电流为900 A。在实际应用中，样本数据越充足越能涵盖运行工况的特征。

3.1 数据特征量概率分布计算

将3 d共36 h的数据组合成1条平滑波动I-t曲线，数据采样频率为3 s。如图3所示，计算该曲线幅值分布、电流变化率、充放电转换次数的分布情况，结果如图4—5所示，充放电转换次数共319次，占所有点数的7.08%。

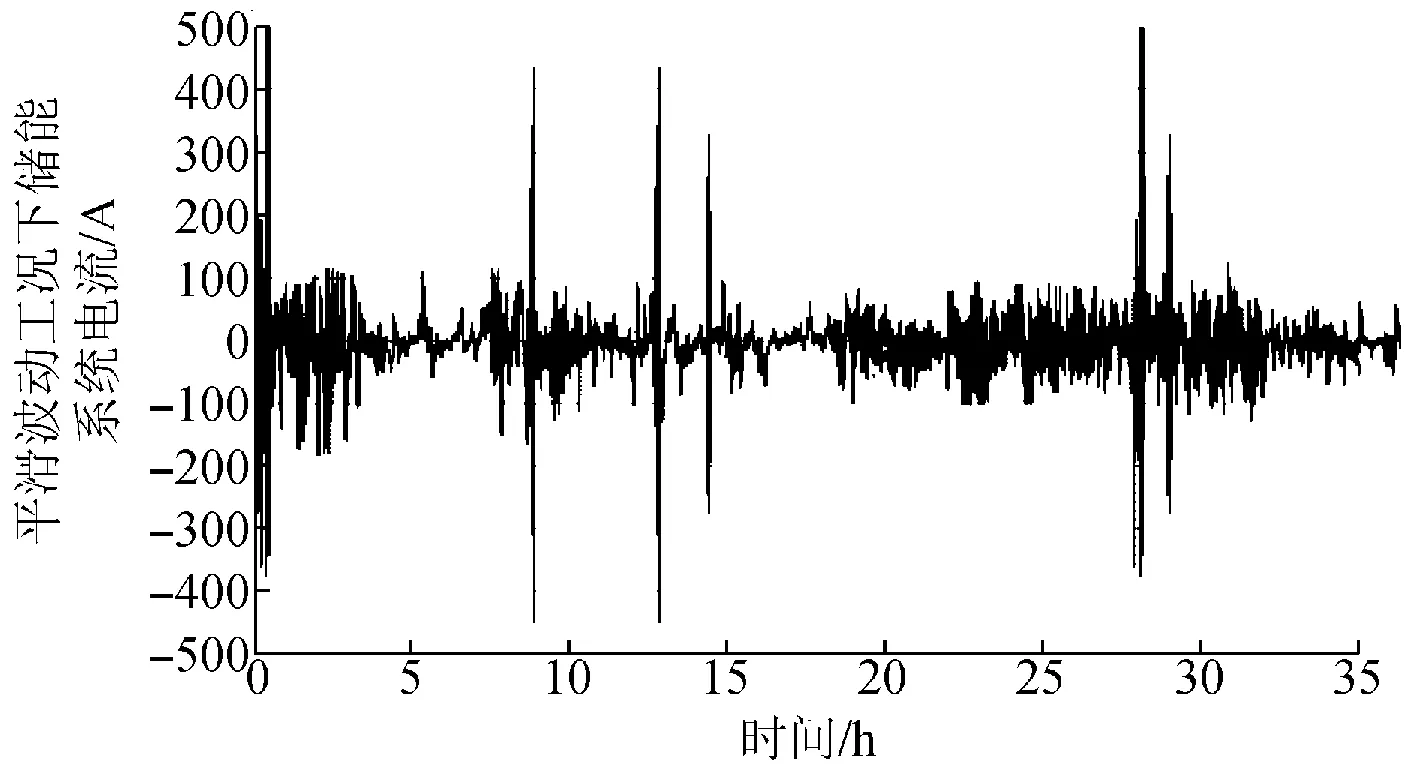
图3 真实时长36 h平滑波动工况运行曲线Fig.3 Operation curve for real time 36 hour under smoothing fluctuation condition

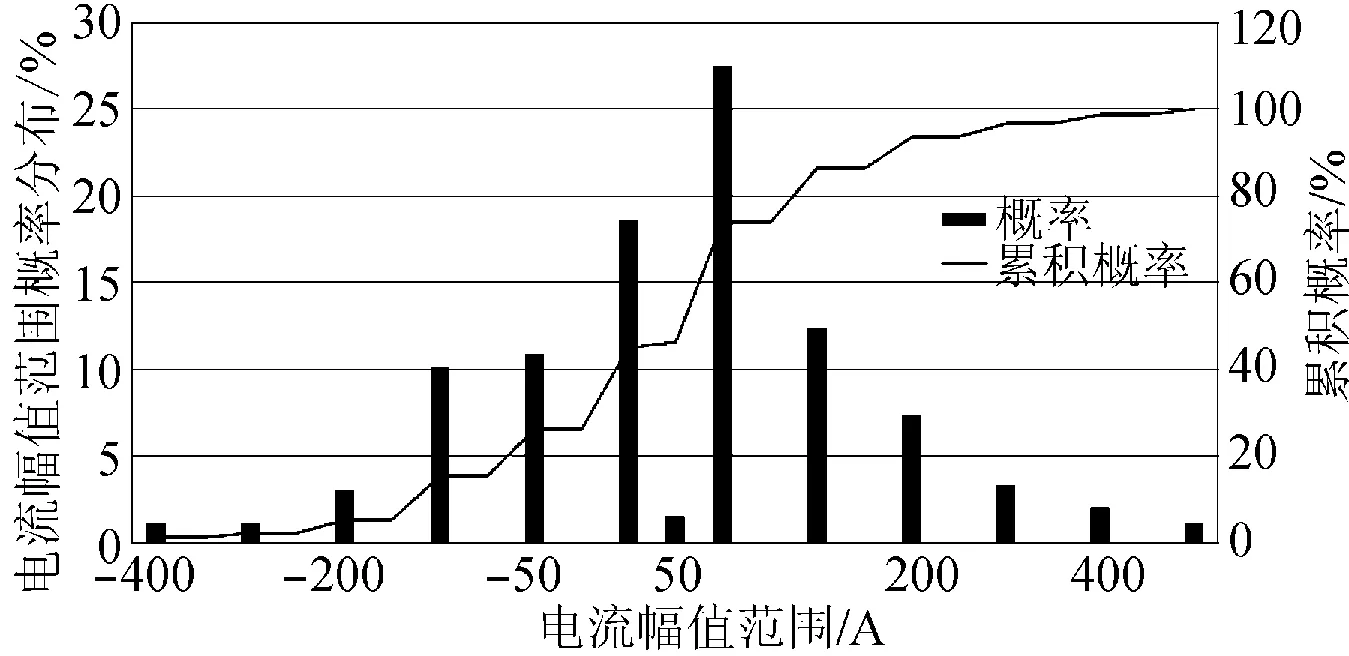
图4 电流幅值概率分布Fig.4 Probability distribution of current amplitude

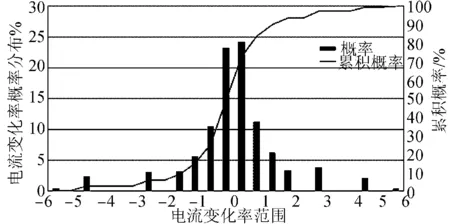
图5 电流变化率概率分布Fig.5 Probability distribution of current change rate

3.2 曲线分段及误差计算

将上述36 h的电流与时间的曲线分段，每 10 min一段，共得出约216个小片段，计算每个小片段的特征量概率分布信息。

在216个小片段中，随机选取6个小片段，组成一个时长为1 h的I-t曲线L，计算L的特征量概率分布信息。

求L的特征量概率分布信息与总工况特征量概率分布信息之间的误差：L的每个电流幅值分布概率(共13个)与总工况的对应部分相减，求出1个均方根误差e1；L的每个电流变化率分布概率(共14个)与总工况的对应部分相减，求出1个均方根误差e2；同理，求充放电转换次数概率的误差e3；3个误差值求平均，得到总误差e。

3.3 典型工况的修正

输出总误差e小于2%的任意组合，计算合成工况的充放电量，如图6所示，充入容量为28.91 A·h；放出容量为36.85 A·h。

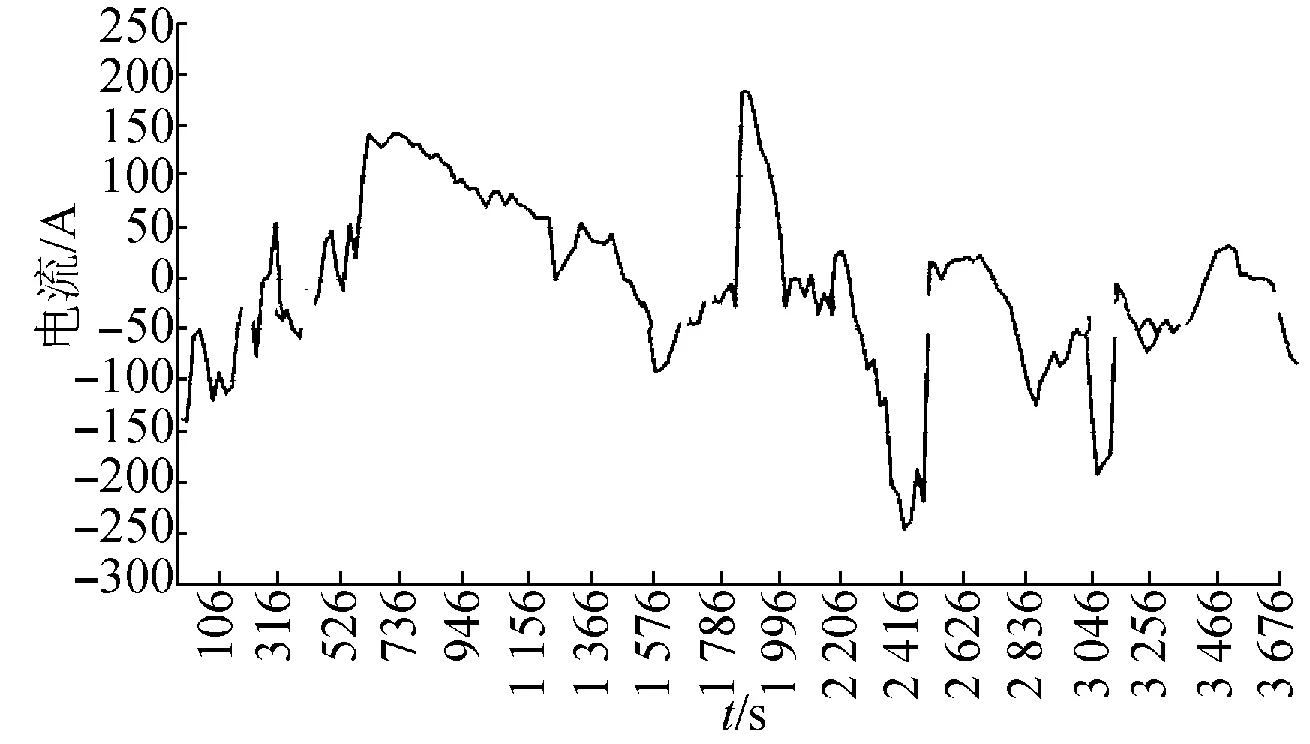
图6 平滑波动典型工况Fig.6 Typical operating condition of smoothing fluctuation

观察典型工况幅值分布，以概率较低、但幅值较大的电流补充电量，使典型工况中充入电量与放出电量接近。选取200，300，400 A电流各充电14 s，充放电量代数和为0.031。最终合成典型工况曲线如图7。同理，可以得出跟踪计划发电、削峰填谷、调频工况的典型工况。

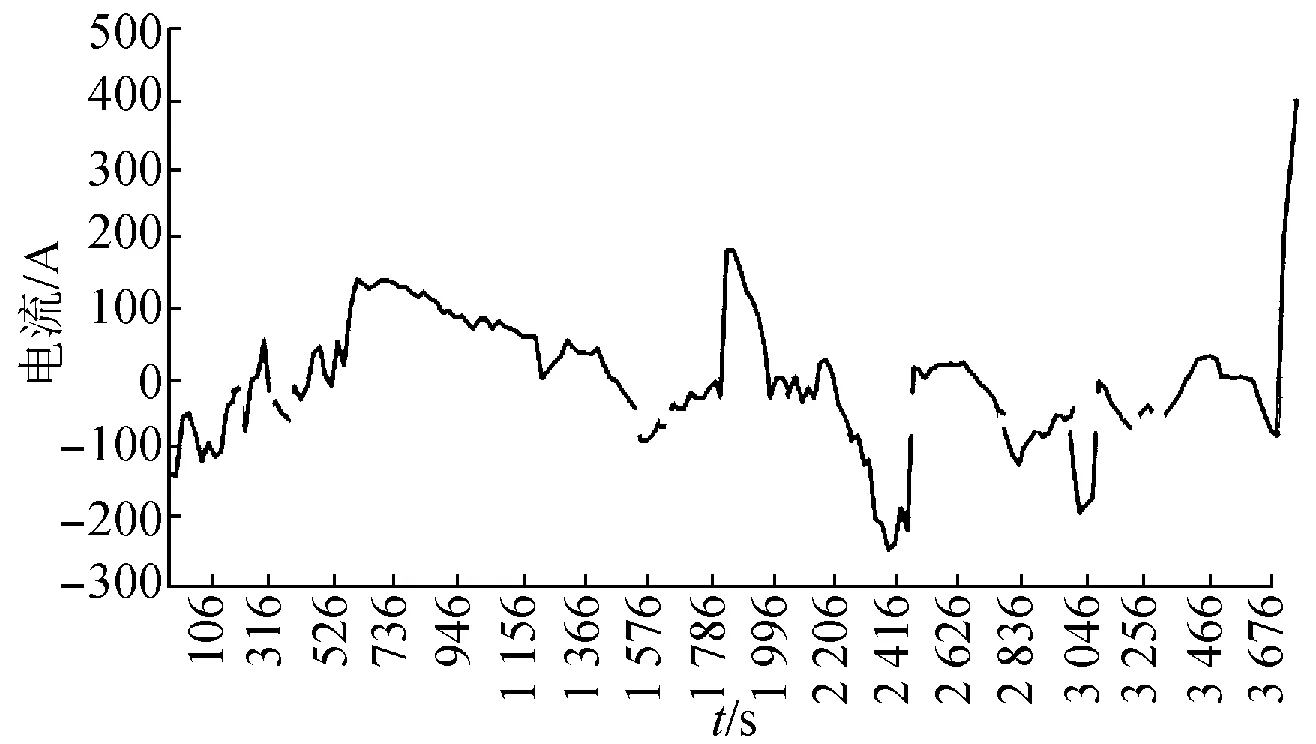
图7 考虑起始SOC的平滑波动典型工况Fig.7 Typical operating condition of smoothing fluctuation with considering initial SOC

4 典型工况的试验应用

本试验对象为来自不同生产厂商的磷酸铁锂电池模组A和模组B，模组A额定参数为240 (A·h)/ 2.8 kW/8.3 (kW·h)；模组B额定参数为198 (A·h)/3.8 kW/7.6 (kW·h)。试验设备为EVTS-150V250A1CH、通道辅助电压/温度测试系统；试验工况为平滑波动工况300 h循环。对循环前后电池模组性能进行分析。

(1)容量。对比电池模组A和B循环前后容量大小，情况见表1和表2。

表1 模组A循环前后容量大小对比
Table 1 Capacity comparison of module A before and after cycle

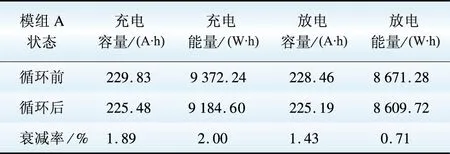
表2 模组B循环前后容量大小对比Table 2 Capacity comparison of module B before and after cycle

(2)电压一致性。循环前充电电压一致性曲线如图8所示，蓝色为电压最大值，红色为电压最小值，绿色为电压最大值与最小值的差。模组A循环前放电过程中电压极差最大值为0.278 7 V；充电过程中电压极差最大值为0.247 9 V。

图8 电池模组循环前后电压一致性Fig.8 Voltage consistency before and afterbattery modulecycle

循环后，放电过程中电压极差最大值为0.327 8 V；充电过程中电压极差最大值为 0.324 4 V。模组B循环前后电压一致性几乎无变化。

试验结论为，经过300 h平滑波动循环工况试验后，模组A充电容量衰减1.89%，放电容量衰减1.43%；单体间电压极差增大。模组B稳定性较好，各项参数变化不明显，因此应用于该种工况的储能电站，在产品选型时可考虑模组B。

5 结 论

本文以在运储能电站运行数据为基础，提出以充放电电流幅值概率分布、电流变化率概率分布、充放电转换次数为特征的大容量电力储能运行典型工况提取方法，为了便于实验室试验，综合考虑了典型工况循环周期内SOC变化约等于0，并以平滑波动工况为例进行了试验验证。形成结论如下：

(1)对于电池工作环境稳定的储能电站，运行于平滑波动、跟踪计划发电、削峰填谷等工况时，其主要特征主要体现在电流的幅值分布、电流变化率分布及充放电转换次数3个方面；

(2)以历史运行曲线为基础，采用截取多个小片段组成短时工况，使特征值概率分布与真实运行曲线概率分布接近，合成大容量电力储能运行典型工况，可用于模组寿命测试和电池选型配置等；

(3)在典型工况设计中，考虑充入电量与放出电量接近，则可以减少循环试验中的SOC调整；

(4)通过试验模拟，证实本方法可以为电力储能电池模组设备选型和性能评估提供技术手段。

[1]中关村储能产业技术联盟(CNESA)． 储能产业研究白皮书2016[M]．北京， 2016.

[2]罗伟林, 张立强,吕超,等.锂离子电池寿命预测国外研究现状综述[J].电源学报,2013,11(1):140-143． LUO Weilin, ZHANG Liqiang, LYU Chao, et al. Review on foreign status of life prediction of lithium-ion batteries[J]. Journal of Power Supply, 2013,11(1):140-143.

[3]马苓,杜光远,徐强,等.锂离子电池容量衰减机理的研究进展[J].电源技术,2014,38(3):553-556． MA Ling,DU Guangyuan, XU Qiang, et al. Progress of capacity fading mechanisms for lithium-ion batteries[J]. Chinese Journal of Power Sources,2014,38(3):553-556.

[4]戴海峰,周艳新,顾伟军,等. 电动汽车用动力锂离子电池寿命问题研究综述[J].电源技术,2014,38(10):1952-1954． DAI Haifeng, ZHOU Yanxin, GU Weijun, et al. Review on life studies of traction Li-ion batteries in electric vehicles[J]. Chinese Journal of Power Sources, 2014,38(10):1952-1954.

[5] 刘卓然,陈健,林凯,等.国内外电动汽车发展现状与趋势[J].电力建设, 2015,36(7):25-31 LIU Zhuoran, CHEN Jian, LIN Kai, et al. Domestic and foreign present situation and the tendency of electric vehicles[J].Electric Power Construction, 2015,36(7):25-31.

[6] 国家环境保护总局. 轻型汽车排气污染物排放限值及测量方法：GB 18352.1—2001[S]. 北京：中国标准出版社，2001.

[7]孙逢春,孟祥峰,林程,等.电动汽车动力电池动态测试工况研究[J].北京理工大学学报,2010,30(3):298-301． SUN Fengchun, MENG Xiangfeng, LIN Cheng, et al. Dynamic stress test profile of power battery for electric vehicle[J]. Transactions of Beijing Institute of Technology, 2010,30(3):298-301.

[8]时玮,姜久春,张维戈,等. 纯电动公交车动力电池寿命测试行驶工况的研究[J].汽车工程,2013,35(2):138-142． SHI Wei，JIANG Jiuchun，ZHANG Weige，et al. A study on the driving cycle for the life test of traction battery in electric buses[J]. Automotive Engineering,2013,35(2):138-142.

[9]叶磊,杨杰.基于典型城市工况的电动汽车用动力电池非恒流放电测试研究[J].客车技术与研究,2013，35(6): 41-44． YE Lei, YANG Jie. Research on inconstant- current discharging testing based on typical city- bus cycle of power battery for electric vehicle[J]. Bus & Coach Technology and Research, 2013，35(6): 41-44.

[10] 庄继晖,谢辉,严英.基于GPRS的电动汽车道路行驶工况自学习[J]. 天津大学学报,2010,43(4):283-286． ZHUANG Jihui，XIE Hui，YAN Ying. GPRS based driving cycle self-learning for electric vehicle[J]. Journal of Tianjin University,2010,43(4):283-286.

[11]高明杰,惠东,高宗和,等. 国家风光储输示范工程介绍及其典型运行模式分析[J].电力系统自动化,2013,37(1):59-63． GAO Mingjie, HUI Dong, GAO Zonghe,et al. Presentation of national wind/photovoltaic/energy storage and transmission demonstration project and analysis of typical operation mode[J]. Automation of Electric Power System, 2013,37(1):59-63.

[12]陈跃燕,李相俊,韩晓娟,等.基于移动平均法和风电波动率约束的电池储能系统平滑风电出力控制策略[J].电力建设,2013,34(7):1-5. CHEN Yueyan, LI Xiangjun, HAN Xiaojuan,et al. Control strategy of smoothing wind power output using battery energy storage based on moving average method and wind power volatility rate constraint[J]. Electric Power Construction,2013,34(7):1-5.

[13] LI X. Fuzzy adaptive kalman filter for wind power output smoothing with battery energy storage system[J].IET Renewable Power Generation,2012,6(5):340-347.

[14]彭思敏.电池储能系统及其在风—储孤网中的运行与控制[D]. 上海：上海交通大学,2013. PENG Simin. Battery energy storage system and its operation and control in the isolated grid based on wind-battery[D]. Shanghai：Shanghai Jiao Tong University,2013.

[15] 陈满,陆志刚,刘怡,等.电池储能系统恒功率削峰填谷优化策略研究[J].电网技术,2012,36(9):232-233． CHEN Man，LU Zhigang，LIU Yi，et al. Research on optimal peak load shifting strategy of battery energy storage system operated in constant power mode[J]. Power System Technology, 2012,36(9):232-233.

[16]陈大宇,张粒子,王澍,等. 储能在美国调频市场中的发展及启示[J].电力系统自动化,2013,37(1):9-13． CHEN Dayu, ZHANG Zili, WANG Shu,et al. Development of energy storage in frequency regulation market of united states and its enlightenment[J]. Automation of Electric Power System, 2013,37(1):9-13．

(编辑 张媛媛)

Test Condition Design Method of Power Energy Storage System Based on Operation Probability Characteristics

BAI Kai

(State Grid Jibei Electric Power Co.,Ltd. Electric Power Research Institute, Beijing 100045, China)

At present, the batteries used in the large-capacity energy storage power station are mostly the products manufactured by electric vehicle battery production line, so their performance test methods are mostly standard working conditions or electric vehicle driving conditions. Through the analysis on the historical operation data of large-capacity energy storage power station, this paper proposes a design method of large-capacity energy storage power station under typical test condition, which takes the distribution of current amplitude, the change rate of current and the conversion time of charge and discharge as eigenvalue, and comprehensively considers the algebraic sum of energy transfer as zero in a repeat cycle. The total error of the eigenvalue probability distribution is less than 2% between the typical test conditions in the examples and the real operating conditions. Finally, this paper completes the performance degradation laboratory test of lithium battery module based on typical test conditions, which can provide the technical support for the battery selection and performance evalution of energy storage power station.

energy storage system; probability distribution; typical condition; performance deterioration

国家电网公司科技项目(电动汽车电池规模化梯次利用关键技术深化研究)

TM 711， TM 911

A

1000-7229(2016)08-0155-06

10.3969/j.issn.1000-7229.2016.08.024

2015-12-28

白恺(1971)，女，高级工程师，研究方向为新能源发电及并网技术等。