基于机会约束规划的储能系统跟踪光伏发电计划出力控制方法

杨婷婷，李相俊，齐磊，张节潭

(1.华北电力大学电气与电子工程学院，北京市 102206；2.新能源与储能运行控制国家重点实验室(中国电力科学研究院)，北京市 100192；3.国网青海省电力公司电力科学研究院，西宁市 810008)

基于机会约束规划的储能系统跟踪光伏发电计划出力控制方法

杨婷婷1，李相俊2，齐磊1，张节潭3

(1.华北电力大学电气与电子工程学院，北京市 102206；
2.新能源与储能运行控制国家重点实验室(中国电力科学研究院)，北京市 100192；
3.国网青海省电力公司电力科学研究院，西宁市 810008)

为最大程度提高光伏系统跟踪计划出力能力，基于短期光伏发电预测功率及预测误差的随机性，提出采用机会约束规划的储能系统控制方法。该方法以光储联合出力在调度计划上下限范围内为目标，考虑储能充放电功率与荷电状态(state of charge，SOC)约束条件，并采用基于蒙特卡罗(Monte Carlo)模拟的改进自适应粒子群优化算法(particle swarm optimization algorithm，PSO)进行求解，进而获得日前各时刻储能的充放电功率值。以典型光伏电站出力为例进行仿真，对比分析了固定系数和变化系数情况下光储跟踪计划出力效果与储能情况，结果验证了该控制策略的有效性与灵活性，并为日前储能充放电控制提供了参考方案。

光储联合发电；跟踪计划出力；机会约束；蒙特卡罗(Monte Carlo)模拟；粒子群优化算法(PSO)

(China Electric Power Research Institute), Beijing 100192, China；3. Electric Power Research Institute of State Grid Qinghai Electric Power Company, Xining 810008, China)

0 引 言

太阳能被公认是未来最具竞争力的能源之一，具有资源丰富、绿色环保等特点。据国际能源署(international energy agency，IEA)预测，到2050年，太阳能光伏发电将占全球发电量的20%～25%，成为基础能源之一[1]。近年来，中国光伏发电市场发展迅猛，年装机容量从2010年的0.5 GW增长为2014年的 10 GW以上，新增量居全球首位[2]。然而光伏发电是间歇性能源，受太阳辐射强度、环境温度等影响，其输出功率具有不确定性，在并网时通常会对电能质量、供电可靠性、电网效益等造成不良影响。通过对光伏电站出力进行预测，有助于电力系统调度部门统筹安排常规能源和光伏发电的协调配合，及时调整调度计划，合理安排电网运行方式，有效降低光伏接入对电力系统的影响，从而提高电网运行的稳定性和安全性。但是，目前，由于光伏发电预测受到自然条件影响，仍存在功率预测误差值过大的问题。为弥补这一不足，利用储能系统对光伏实际功率与计划出力间的差额进行补偿跟踪，将光储联合发电系统变成常规的确定性电源，从而提高光伏发电的预测精度已成为新的研究热点[3-7]。

目前，国内外针对光伏预测技术已展开多项研究，而基于光储联合应用的分析则很少，尤其针对储能控制实现光储跟踪计划出力的研究更是鲜见公开报道。文献[8]提出基于机会约束规划理论的日前储能优化控制方法，以风光储出力曲线与固定计划出力曲线相似度最大为目标，仿真结果实现了风光储出力与固定计划功率曲线的高度一致，但由于该方法未考虑风光发电预测误差的上下限范围，使得储能系统的控制失去了一定的灵活性。文献[9]则提出基于模糊相关机会规划理论的跟踪计划策略，以1日内所有时段的可信度均值最大为目标，但同样与文献[8]类似，只考虑了跟踪固定计划出力曲线。文献[10]基于超短期风电预测功率建立了包含5个控制系数的储能系统充放电控制策略，通过滚动变化系数取得了有效的跟踪计划出力效果，但未考虑光伏发电波动及其随机性的影响。

在现有文献研究的基础上，本文提出基于短期光伏预测功率的储能系统跟踪计划出力日前优化调度策略。根据2013年国家能源行业编制完成的《光伏发电功率预测系统功能规范》[11]中短期预测误差最大不超过25%的规定，来制定光伏计划出力上下限；以光储联合发电出力在计划出力范围内为目标，将预测误差处理为随机变量，运用机会约束理论建立数学模型，采用基于蒙特卡罗(Monte Carlo)模拟的改进自适应粒子群优化算法(particle swarm optimization algorithm，PSO)进行求解，并获得光储跟踪计划出力时储能的充放电方案；通过算例调整目标函数中的控制系数，进一步证明该策略的灵活性，实现光储在保证跟踪计划出力目标的同时，并不对储能系统造成多余的负担。

1 机会约束规划理论

1.1 机会约束规划

在现实生活中制定决策时，经常会遇到不确定现象，对于这些不确定规划问题，经典的优化理论通常是无能为力的。根据现象描述参数类型的不同，不确定规划通常分为随机规划和模糊规划。机会约束规划为随机规划的一种，其主要针对约束条件中含有随机变量，且必须在观测到随机变量实现前作出决策的问题。与传统优化中硬性约束条件不同，机会约束规划允许所作决策在一定程度上不满足约束条件，该决策使约束条件成立的概率只需不小于某一置信水平即可[12-13]。机会约束规划的常见形式为

(1)

式中：x为决策向量；ξ为已知概率密度分布函数φ(ξ)的随机变量；f(x)为目标函数；gj(x,ξ)为随机机会约束函数；Pr{}表示事件成立的概率；α为给定的置信水平。

1.2 蒙特卡罗模拟技术

蒙特卡罗模拟是一种实现随机系统抽样实验的技术，其基础是从给定的概率分布中抽取随机变量。蒙特卡罗模拟技术在随机优化问题中的应用主要有目标函数的期望值估计和估计事件发生的概率。采用蒙特卡罗模拟检验机会约束成立与否的过程如下。

首先从概率分布中产生N个独立的随机变量，n是N次实验中成立的次数，即所产生的随机变量中满足机会约束的个数。由大数定律，可以用频率估计概率，因此，当且仅当频率n/N≥α时，机会约束条件成立。具体步骤为：(1)置n=0；(2)由概率分布φ(ξ)产生随机变量ξ；(3)如果gj(x,ξ)≤0，j=1，2，…，p，则n++；(4)重复步骤(2)和(3)共N次；(5)如果n/N≥α，则返回“成立”，否则返回“不成立”[14]。

因此，结合蒙特卡罗模拟和机会约束规划，实现了对光伏发电随机性的模拟与储能系统置信度的判断，从而使利用储能系统跟踪光伏发电计划的日前优化调度过程所考虑因素更加全面。

2 储能优化控制策略

2.1 目标函数

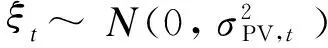
(2)

(3)

以短期光伏发电功率预测值为依据，根据《光伏发电功率预测系统功能规范》要求，按照±25%波动制订当日调度计划范围，短期光伏功率预测技术的预测时间尺度为0～24 h，预测时间分辨率为15 min。策略控制目标即为最大程度使得光储联合出力在调度计划上下限范围内。

Plimit=εallowCap

(4)

(5)

(6)

Pplan_adj,t=u[Pplan_dn,t+
c(Pplan_up,t-Pplan_dn,t)]

(7)

(8)

(9)

式中：Plimit为εallow决定的光伏出力波动限值；εallow为日前预测误差允许的百分值，按规定为25%；Cap为光伏装机容量；Pplan_up,t和Pplan_dn,t分别为每个时段光伏计划出力上下限值；Pplan_adj,t为跟踪光伏发电目标控制功率；u为控制储能系统的开关系数，取0或1，0表示储能系统处于空闲状态，1表示储能系统处于工作状态；c为介于0到1之间的目标功率大小控制系数；m为总的时段数；Pbess,t为决策变量，即t时刻储能系统充放电功率，Pbess,t>0，表示储能系统放电，Pbess,t<0，表示储能系统充电；εt为每个时段的预测误差率。

2.2 约束条件

2.2.1 机会约束条件

通过采用机会约束条件可以将预测误差随机性的影响考虑在模型中。因此本文将光伏有功功率输出平滑率的绝对值不高于允许范围δ(取0.1)作为机会约束条件，使其成立的概率不小于置信水平α，相比约束条件100%成立，通过小概率违反约束条件可降低对储能系统的要求[17-18]。

(10)

(11)

2.2.2 储能系统约束条件

(1)功率约束

充电时，

Pch,max≤Pbess,t≤0

(12)

放电时，

0≤Pbess,t≤Pdis,max

(13)

式中：Pch,max为负值，表示储能系统的最大允许充电功率，MW；Pdis,max为正值，表示储能系统的最大允许放电功率，MW。

(2)荷电状态(state of charge，SOC)约束

SOC是指储能系统的剩余容量与其完全充电状态的容量的比值，常用百分数表示。

CSOC,min≤CSOC,t≤CSOC,max

(14)

CSOC,t的求解公式为

(15)

式中：CSOC,min为储能系统荷电状态的最小值；CSOC,max为储能系统荷电状态的最大值；CSOC,t为t时刻的荷电状态；C为储能系统容量；ζ为充放电效率，本文取0.8。

3 模型求解

3.1 改进自适应粒子群优化算法

粒子群优化算法源于对鸟类捕食行为的研究，通过在可行空间中初始化粒子，建立速度-位置模型来不断更新粒子，进而找到问题的最优解[19]。用式(16)和式(17)更新粒子的速度和位置。

(16)

(17)

式中：c1，c2为学习因子，可以加快收敛，避免陷入局部最优；r1，r2是[0,1]间的随机数；K为约束因子；ω为惯性权重。为防止盲目搜索，通常将粒子位置和速度限制在一定区间[-Xmin，Xmax]与[-Vmin，Vmax]。

虽然基本的粒子群算法收敛速度很快，但易于陷入局部最优，因此采用改进的PSO算法。在PSO基本算法中，K与ω均为1，本文采用改进的自适应粒子群算法对K与ω进行调整，即

(18)

式中φ=c1+c2。

(19)

式中：k为当前的粒子迭代次数；kmax为粒子群算法开始设置的最大迭代次数；ωmin、ωmax分别是最小和最大惯性权重。

3.2 具体算法流程

结合蒙特卡罗模拟采用改进自适应PSO算法求解本文机会约束规划模型的具体步骤如下。

(1)读取短期光伏预测出力数据，制定调度计划出力上下限范围，基于公式(2)模拟当日实际光伏出力，并根据式(7)设定当日跟踪光伏发电控制功率目标值。

(2)设定PSO算法与蒙特卡罗模拟技术的基本参数，设定储能系统充放电功率范围、SOC范围以及SOC的初始值。

(3)在储能系统充放电功率范围中随机选取每个粒子每个时段对应储能充放电功率，并采用大数定律进行机会约束条件验证。若满足，则重复该步骤来初始化N个粒子种群，否则继续进行随机选取直至验证满足。

(4)根据式(8)目标函数计算初始种群中每个粒子的适应度值，确定个体最优Pbest与全局最优Gbest。

(5)更新粒子的速度与位置，对新的粒子同样按照步骤(3)进行约束条件验证。若不满足，则重新对粒子进行更新。

(6)对新的粒子计算适应度值。若结果好于当前Pbest，则更新Pbest；若所有粒子Pbest中最佳的好于当前Gbest，则更新Gbest。

(7)判断迭代次数是否超过最大迭代次数或最优值在若干代中是否不再更新。若否，返回步骤(5)；若是，则停止迭代，输出最优解。

(8)根据优化算法获得的最优解按照式(15)计算每个时段的SOC值。经判断，若SOC在规定范围内，则所求储能系统充放电功率值合理；若超出范围，则返回步骤(1)对跟踪光伏发电功率目标值中的控制系数u和c进行调节，重新进行计算。

4 算例分析

以某风光储示范工程为背景，选取7月份某日短期光伏预测数据作为算例分析对象。该示范工程中光伏发电总装机容量为40 MW，储能总装机容量为20 MW/70 MW·h，设定储能系统初始荷电状态为0.5，CSOC,min=0.2，CSOC,max=0.8，则对应初始电量E0=35 MW·h，Emin=14 MW·h，Emax=56 MW·h。PSO中参数设置：种群规模为40；粒子维数为96；c1=c2=1.496 2；ωmin=0.4；ωmax=0.9；粒子速度范围为[-3,3]；最大迭代次数取500。蒙特卡罗模拟次数设为150。

图1为该示范工程7月份某日短期光伏预测数据，根据实际物理情况，按照《光伏发电功率预测系统功能规范》中相应预测出力的±25%波动，制订该日光伏调度计划上下限出力范围,并通过蒙特卡罗模拟获得当日0～24 h的实际光伏出力。

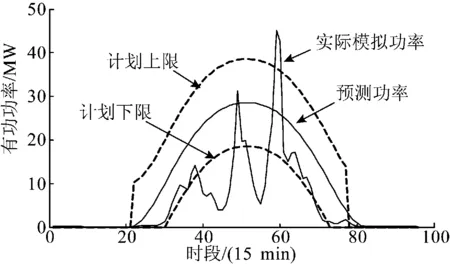
图1 短期光伏预测功率、计划上下限与日前实际功率模拟曲线Fig.1 Curves of short-term PV prediction power, upper and lower range of schedule plan, and day-ahead actual simulated power

为验证本文所提控制策略的有效性与灵活性，算例分别在固定系数情况与变化系数情况下进行仿真计算对比。固定系数情况中设置储能开关系数u=1，保持储能系统始终处于工作状态。为使光储联合出力更易在误差范围内，应选择目标控制功率尽可能接近计划上下限，本算例中固定目标功率大小控制系数c为0.8和0.2。图2为固定系数情况下控制系数变化曲线以及光储跟踪计划出力效果图。由图2可以看出本文的控制策略可以有效地实现光储联合跟踪计划出力的目标，实际光伏出力在储能系统的补充下基本都限制在了计划上下限范围内。图3为变化系数情况下控制系数变化曲线及光储跟踪计划出力效果图。图4为各情况下SOC变化曲线。从图4中可发现，c取0.8时，储能系统在1天内大部分时段是一直处于工作状态，并且放电深度较c取0.2时更深，最后超出了算例中SOC的下限范围，这是不符合实际要求的。而c取0.2时，储能系统的SOC变化趋势虽基本是合理的，但对储能系统的要求还是很高。为降低储能负担，在固定系数c=0.2的基础上对充放电功率约束条件进行改进，使储能系统只在实际光伏出力低于计划下限的时段放电，超出计划上限的时段充电，其余时段保持空闲状态来对开关系数u进行调节，如图3所示，仿真结果达到了预期效果。

从图4中可看出，在固定系数情况的基础上优化调节控制系数后进行仿真所得储能系统的SOC变化曲线明显是最优的，变化系数后储能只是在少部分时段进行工作，其余大部分时段都处于空闲状态，这对延长储能系统使用寿命也是有利的。另外每次充放电都在算例SOC上下限范围内进行，在充/放电之前都会进行一定量的放电/充电准备，提高了储能系统的充放电能力。

图2 固定系数情况下控制系数变化曲线以及光储跟踪计划出力效果图Fig.2 Curves of control coefficients under fixed coefficients situation and PV/energy storage tracking effects

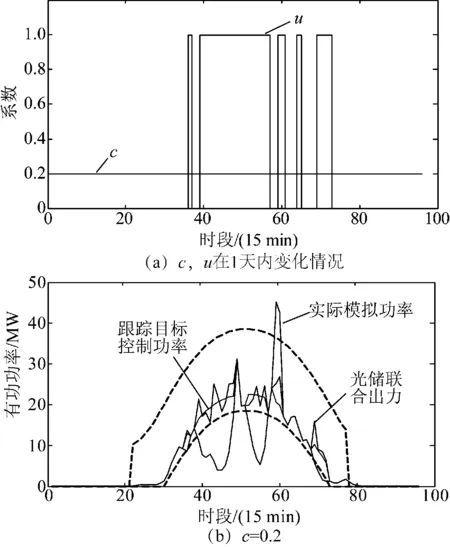
图3 变化系数情况下控制系数变化曲线以及光储跟踪计划出力效果图Fig.3 Curves of control coefficients under changed coefficients situation and PV/energy storage tracking effects

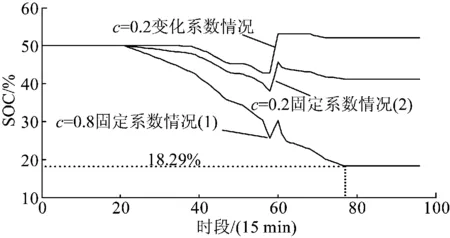
图4 各情况下SOC变化曲线Fig.4 SOC curves under every situation

为进一步验证变化系数情况下仿真效果更优，图5又对未加储能，加储能后固定系数(c=0.2)和变化系数情况下，具体的跟踪程度形成直方图作量化对比分析，按照公式(9)计算每个时段的预测误差率。将误差率分为间隔为5%的区间，对各情况中误差落在各个区间的概率通过直方图进行统计，可以看出加入储能后将误差值大幅度降低。按照《光伏发电功率预测系统功能规范》中规定，日预测最大误差小于25%的要求，表1又对各情况下将预测误差限制在该范围内的概率进行了计算，对比分析了各方案减小预测误差，提高预测精度的程度。结果表明，变化系数后不仅对储能要求降低了，更可以100%将误差减小并限制在合格范围内。

图5 加储能前后日预测误差概率分布直方对比图Fig.5 Histogram comparison of prediction error before and after energy storage

通过以上综合分析跟踪计划出力效果，提高预测精度程度以及储能系统的工作情况，可以采用变系数控制策略作为参考方案来对当日的储能进行控制，具体各个时段充放电功率值如图6所示，总的充放电电量如表2。相比于固定系数情况，在调整控制系数后，由于在大部分时段储能系统不需要参与控制，因此，总的放电电量大幅度降低。

图6 c=0.2各情况下储能充放电功率Fig.6 Charge and discharge power of energy storage under c=0.2

群进化过程如图7所示，可看出，适应度值随着进化代数的增加逐渐减小，表明光储联合出力曲线与目标控制功率曲线越来越接近。在本算例参数设置下，迭代次数达到200次(其他光储参数算例背景情况下迭代收敛次数会相应发生变化)附近时适应度值便达到最优，基本不再发生变化，这说明了算法具有良好的收敛性。

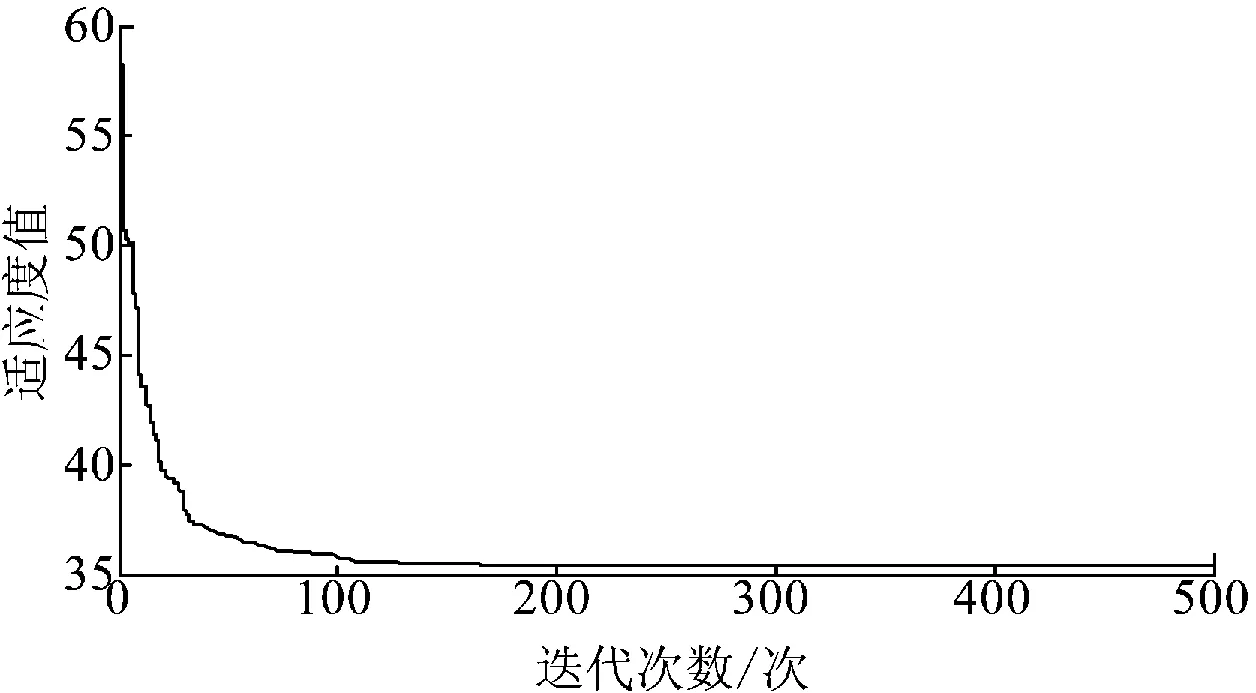
图7 粒子群算法收敛曲线Fig.7 Convergence curve of PSO

表3为置信水平取不同值时的计算结果比较。置信水平在0.65左右时，误差合格率相比于未加储能时提高并不多，说明跟踪效果不够理想；置信水平在0.75以上时，随着置信水平的提高，满足误差要求合格程度都基本达到了90%以上，但需要的总充放电量逐渐增大，对储能系统的要求也更加严格，实际跟踪控制中可根据储能系统具体情况来选择适宜的置信水平来进行计算。

表3 不同置信水平计算结果比较
Table 3 Comparison of different confidence levels

5 结 论

本文基于短期预测功率制订光伏发电计划出力上下限范围，考虑预测偏差随机性，建立机会约束规划数学模型，利用基于蒙特卡罗模拟的改进自适应粒子群算法求解储能系统出力。研究结果表明光储联合跟踪计划出力达到了良好的效果。同时本文考虑了储能实际应用的可行性，通过设置控制系数来随时调整跟踪目标功率，与固定系数控制策略相比，变系数控制策略使得日前储能出力控制方案更加灵活，对储能系统的要求进一步降低。

[1]崔洋，孙银川，常倬林. 短期太阳能光伏发电预测方法研究进展[J]. 资源科学，2013，35(7)：1474-1481. CUI Yang，SUN Yinchuan，CHANG Zhuolin. A review of short-term solar photovoltaic power generation prediction methods[J]. Resources Science，2013，35(7)：1474-1481.

[2] 崔杨，陈正洪，成驰，等. 光伏发电功率预测预报系统升级方案设计及关键技术实现[J]. 中国电力，2014，47(10)：142-147. CUI Yang，CHEN Zhenghong，CHENG Chi，et al.Upgrade of the PV power prediction system and implementation of the key technologies[J]. Electric Power，2014，47(10)：142-147.

[3]袁晓玲，施俊华，徐杰彦. 计及天气类型指数的光伏发电短期出力预测[J]. 中国电机工程学报，2013，33(34)：57-64. YUAN Xiaoling，SHI Junhua，XU Jieyan. Short-term power forecasting for photovoltaic generation considering weather type index[J]. Proceedings of the CSEE，2013，33(34)：57-64.

[4]陈炜，艾欣，吴涛，等. 光伏并网发电系统对电网的影响研究综述[J]. 电力自动化设备，2013，33(2)：26-32, 39. CHEN Wei，AI Xin，WU Tao，et al.Influence of grid-connected photovoltaic system on power network[J]. Electric Power Automation Equipment，2013，33(2)：26-32, 39.

[5]罗建春，晁勤，罗洪，等. 基于LVQ-GA-BP神经网络光伏电站出力短期预测[J].电力系统保护与控制，2014，42(13)：89-94. LUO Jianchun，CHAO Qin，LUO Hong，et al. PV short-term output forecasting based on LVQ-GA-BP neural network[J]. Power System Protection and Control，2014，42(13)：89-94.

[6]靳文涛，李蓓，谢志佳. 电池储能系统在跟踪风电计划出力中的需求分析[J]. 储能科学与技术，2013，2(3)：294-299. JIN Wentao，LI Bei，XIE Zhijia. An analysis for the need of a battery energy storage system in tracking wind power schedule output[J]. Energy Storage Science and Technology，2013，2(3)：294-299.

[7]林少伯，韩民晓，赵国鹏，等. 基于随机预测误差的分布式光伏配网储能系统容量配置方法[J]. 中国电机工程学报，2013，33(4)：25-33. LIN Shaobo，HAN Minxiao，ZHAO Guopeng，et al. Capacity allocation of energy storage in distributed photovoltaic power system based on stochastic prediction error[J]. Proceedings of the CSEE，2013，33(4)：25-33.

[8]赵书强，刘晨亮，王明雨，等. 基于机会约束规划的储能日前优化调度[J]. 电网技术，2013，37(11)：3055-3059. ZHAO Shuqiang,，LIU Chenliang,，WANG Mingyu，et al. Chance-constrained programming based day-ahead optimal scheduling of energy storage[J]. Power System Technology，2013，37(11)：3055-3059.

[9]胡永强，刘晨亮，赵书强，等. 基于模糊相关机会规划的储能优化控制[J]. 电力系统自动化，2014，38(6)：20-25. HU Yongqiang，LIU Chenliang，ZHAO Shuqiang，et al. Optimal control of energy storage based on fuzzy correlated-chance programming[J]. Automation of Electric Power Systems，2014，38(6)：20-25.

[10]闫鹤鸣，李相俊，麻秀范，等. 基于超短期风电预测功率的储能系统跟踪风电计划出力控制方法[J]. 电网技术，2015，39(2)：432-439. YAN Heming，LI Xiangjun，MA Xiufan，et al. Wind power output schedule tracking control method of energy storage system based on ultra-short term wind power prediction[J]. Power System Technology，2015，39(2)：432-439.

[11]国家电网公司. 光伏发电功率预测系统功能规范：Q/GDW1995—2013[S]. 北京：中国电力出版社，2013.

[12] LI Q，CHOI S S，YUAN Y，et al.On the determination of battery energy storage capacity and short-term power dispatch of a wind farm[J].IEEE Transactions on Sustainable Energy，2011, 2(2)：148-158.

[13] LI X，HUI D，LAI X.Battery energy storage station(BESS)-based smoothing control of photovoltaic(PV) and wind power generation fluctuations[J].IEEE Transactions on Sustainable Energy，2013，4(2)：464-473.

[14]刘宝碇，赵瑞清，王纲.不确定规划及应用[M].北京：清华大学出版社，2003：76-85.

[15] 杨水丽，李建林，惠东，等. 用于跟踪风电场计划出力的电池储能系统容量优化配置[J]. 电网技术，2014，38(6)：1485-1491. YANG Shuili，LI Jianlin，HUI Dong，et al.Optimal capacity configuration of battery energy storage system to track planned output of wind farm[J]. Power System Technology，2014，38(6)：1485-1491.

[16] 谢石骁，杨莉，李丽娜. 基于机会约束规划的混合储能优化配置方法[J]. 电网技术，2012，36(5)：79-84. XIE Shixiao, YANG Li, LI Lina. A chance constrained programming based optimal configuration method of hybrid energy storage system[J]. Power System Technology，2012，36(5)：79-84.

[17] 杨宁，文福拴. 基于机会约束规划的输电系统规划方法[J]. 电力系统自动化，2004，28(14)：23-27. YANG Ning，WEN Fushuan. Transmission system expansion planning based on chance constrained programming[J]. Automation of Electric Power Systems，2004，28(14)：23-27.

[18] 沈洲，杨伟，仲海波，等. 基于机会约束规划和随机模拟技术的含风电场电力系统多目标优化调度[J]. 电力学报，2013，28(1)：44-49, 53. SHEN Zhou，YANG Wei，ZHONG Haibo，et al.Power system containing wind farm optimization scheduling with multi-objective based on chance-constrained and random simulation[J]. Journal of Electric Power，2013，28(1)：44-49, 53.

[19]杨珺，张建成，黄磊磊，等. 基于改进粒子群算法的独立光伏发电系统储能容量优化配置研究[J]. 华东电力，2012，40(8)：1370-1374. YANG Jun，ZHANG Jiancheng，HUANG Leilei，et al.Energy storage capacity optimization for independent PV power system based on improved PSO algorithm[J]. East China Electric Power，2012，40(8)：1370-1374.

(编辑 景贺峰)

Control Method of Energy Storage System for Tracking Photovoltaic Power Generation Output Schedule Based on Chance-Constrained Programming

YANG Tingting1, LI Xiangjun2, QI Lei1, ZHANG Jietan3

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China；2. State Key Laboratory of Control and Operation of Renewable Energy and Storage Systems

To maximize the photovoltaic (PV) system tracking scheduleed output, based on the short-term prediction of PV power generation and the randomness of prediction deviation, this paper proposes an energy storage control method that adopts chance-constrained programming. This method takes the PV/energy storage combined output in the upper and lower of scheduled range as the objective, considers the constraints of charge and discharge power and the state of charge (SOC), and adopts improved adaptive particle swarm optimization algorithm (PSO) based on Monte Carlo simulation to obtain day-ahead each time charge and discharge power. Finally, taking a typical PV output for simulation, we compare the PV/energy storage tracking scheduled output effect and energy storage condition in fixed coefficients situation and variation coefficients situation. The results verify the feasibility and flexibility of the proposed strategy, which can provide effective reference scheme for day-ahead energy storage control.

photovoltaic/energy storage combined power generation; tracking scheduled output; chance-constrained; Monte Carlo simulation; particle swarm optimization algorithm(PSO)

北京市科技新星计划项目(Z141101001814094)；国家电网公司科技项目(No.DG71-15-039)Project supported by Beijing New-star Plan of Science and Technology (Z141101001814094); Science and Technology Project of SGCC (DG71-15-039)

TM 73

A

1000-7229(2016)08-0115-07

10.3969/j.issn.1000-7229.2016.08.018

2016-04-27

杨婷婷(1991)，女，硕士研究生，主要研究方向为电池储能系统的运行控制，电力系统分析、运行与控制；

李相俊(1979)，男，博士，教授级高级工程师，主要研究方向为电池储能系统控制、新能源与分布式发电以及电力系统运行与控制；

齐磊(1978)，男，博士，教授，主要研究方向为先进输变电技术以及电力系统电磁兼容；

张节潭(1980)，男，博士，高级工程师，主要研究方向为新能源发电并网、电力系统优化规划。