基于模糊经验模态分解的电池储能系统平滑风电出力控制策略

杨锡运，曹超，李相俊,任杰,高峰,吴子晗

(1.华北电力大学控制与计算机工程学院，北京市 102206；2.上海电气集团股份有限公司中央研究院，上海市 200070；3.中国电力科学研究院，北京市 100192)

基于模糊经验模态分解的电池储能系统平滑风电出力控制策略

杨锡运1，曹超2，李相俊3,任杰1,高峰1,吴子晗1

(1.华北电力大学控制与计算机工程学院，北京市 102206；2.上海电气集团股份有限公司中央研究院，上海市 200070；3.中国电力科学研究院，北京市 100192)

为减少风电波动率，提高并网可靠性，提出一种基于模糊经验模态分解(empirical mode decomposition，EMD)的储能系统平滑风电功率波动的控制策略。采用经验模态分解对风电功率进行滤波，低频分量并网，高频分量并入电池储能系统(battery energy storage system，BESS)。使用平滑后风电波动率和储能电池荷电状态(state of charge，SOC)作为约束条件，利用模糊控制算法，自适应在线调整EMD滤波阶数，通过模糊自适应控制器，能够更好地平滑风电波动。对比其他平抑风电功率储能控制策略，仿真实例表明，该方法可以有效地平抑风电功率波动，避免储能电池过充过放，稳定储能荷电状态。

经验模态分解(EMD)；功率平滑；模糊控制；波动率；荷电状态(SOC)

0 引 言

风能具有间歇性和随机性等特点，风电功率直接并网会对电网产生巨大冲击，影响电网运行的稳定性和安全性。因此，国家出台了风电接入电网的技术规定，保障风电并网质量[1]。在风电场出口处配置一定容量的储能系统，可以有效地平抑风电场的功率波动，提高电力系统的稳定性[2-3]。

储能系统的并网控制策略非常重要，控制不合理很容易导致储能装置出现过充、过放，严重影响储能电池的寿命，并网功率波动过大也会影响电网的稳定性。文献[4]提出基于一阶低通滤波器的储能系统平滑风电功率波动的控制策略。文献[5]利用人工神经网络算法对储能系统进行优化控制，将功率波动控制在较小的范围内。文献[6]采用移动平均法对风电功率进行平滑。但上述文献均没有考虑储能系统的荷电状态(state of charge，SOC)，容易造成储能系统的过度充放电。文献[7-8]考虑储能系统的SOC和低通滤波相结合的方法进行功率平滑，但低通滤波存在迟延的问题，很难克服，低通滤波器的时间常数选择将直接影响风电功率的平滑效果。文献[9]提出了基于定阶经验模态分解(empirical mode decomposition，EMD)的储能容量优化的方法，但未充分考虑波动率及储能系统的SOC，会出现一些时刻波动率不满足并网的要求。

本文提出基于模糊变阶经验模态分解的储能系统平滑风电功率的控制策略。基于经验模态分解的方法，将风电功率信号分解成低频信号和高频信号。低频信号作为并网功率信号；高频信号作为储能电池吸收功率信号，以平抑风电功率波动。由于EMD滤波器的阶次选择会直接影响确定的低频信号和高频信号，从而影响平滑风电出力的效果。提出采用平滑后波动率和储能电池荷电状态为约束条件下的模糊变阶EMD的方法，该方案综合波动率和SOC状况，通过模糊决策在线调节EMD滤波阶数，通过模糊自适应控制器，达到既能防止储能系统出现过充和过放现象，保持储能系统良好性能，又兼具较好的平滑风电输出的效果。对比不同的风电功率平滑策略，仿真验证本方法的有效性。

1 风电功率信号的经验模态分解

1.1 风电功率的频谱分析

风电场的功率变化与风速变化密切相关。风电场的风速特性表现为低频变化占据的幅值成分较大，高频变化的风速幅值较小[10]。因此，风电场功率信号的能量应主要集中在低频部分。采用某49.5 MW风电场2010年半年的实际功率，采样时间为1 min，对该数据进行快速傅里叶变换，得到幅频特性曲线，如图1所示。

由图1可知，风电场功率的能量主要集中在低频部分(0～10-4Hz)，高频部分能量较低。根据频域理论，如果保留其一定带宽的低频成分，重构后的功率信号将包含原功率信号的主要能量，而且重构后的信号在时域上的功率图形将比原时域功率信号平滑。因此，本文将高频功率信号作为储能系统吸收功率的期望值，低频功率信号作为风电并网的期望值。如何合理地分解风电场输出功率的低频信号和高频信号，将影响风电功率的平滑效果，本文采用EMD方法将风电场输出功率信号分解成高频信号和低频信号。

1.2 经验模态分解的基本步骤

EMD分解方法是把原始信号分解成若干个固有模态函数(intrinsic mode function，IMF)和余量。固有模态函数必须满足2个条件[11]：(1)在整个数据序列中，极值点的数量与过零点的数量必须相等，或最多相差不能超过1个；(2)在任一时间点上，信号的局部最大值和局部最小值定义的包络平均值为0。这2个条件使分解得到的IMF是窄带信号。

对于一个时间信号进行EMD分解的步骤如下。

(1)寻找信号的所有极大值和极小值，然后采用三次样条插值算法分别获得信号的上包络线eupp(t)和下包络线elow(t)，并计算出2条包络线的平均值m1(t)为

(1)

(2)设变量x1(t)，令其为

x1(t)=x(t)-m1(t)

(2)

若公式(2)满足IMF的2个条件，则可以将x1(t)作为第1个IMF分量，并记为c1(t)；否则作为原始信号，重复步骤(1)和步骤(2)，直到得到第1个IMF分量。

(3)计算剩余信号r1(t)=x(t)-c1(t)，把其作为新的信号，重复步骤(1)和步骤(2)，直到提取所有IMF分量。当剩余的信号为非振荡的单调函数或小于预定值的常数时，认为分解完毕。原始的数据最终分解为n个IMF分量和1个剩余的rn(t)，即

(3)

1.3 风电功率信号的EMD分解

图2为某风电场某日风电的实际功率，数据采样间隔为1 min。

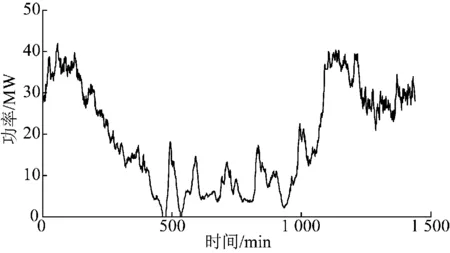
图2 某风电场某日的风电实际功率曲线Fig.2 Curves of real power at a wind farm in a day

采用EMD对风电功率信号进行分解，得到各阶IMF分量，如图3所示。

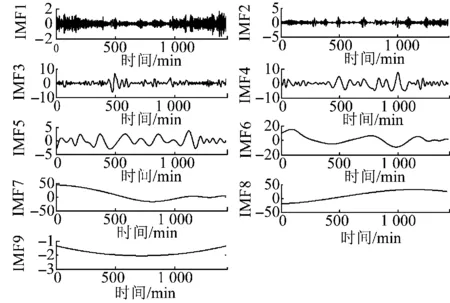
图3 基于EMD的风电功率信号分解曲线Fig.3 Curves of wind power signals decomposed by EMD

由图3可知，IMF分量阶数越高，则其所含瞬时频率成分越低。使用EMD进行滤波时，将k阶之后的所有IMF分量之和的低频部分作为并网输出功率，从第1阶到第k阶的IMF分量之和为高频部分，由储能电池吸收。其中，滤波阶数k的取值将对平滑效果产生很大的影响。本文提出考虑平滑波动率和储能电池SOC约束的模糊变阶EMD的电池储能平抑风电功率的算法。

2 基于模糊变阶EMD的风电功率平滑策略

2.1 基于EMD的风储联合发电系统结构

利用电池储能系统(battery energy storage system，BESS)平滑风电功率波动虽然会增加发电侧的投资成本，但可以提高风力发电站功率输出的稳定性，提高风电并网的稳定性和可调度性，减少因波动率过高而导致的弃风电量，给风电场带来一定的效益。

本文采用经验模态分解方法控制储能系统的出力，平抑风电功率波动。图4为典型的基于BESS的风力发电系统。Pw为t时刻的风电功率；Pbat为风电功率与平抑后系统输出功率的差值；Psmooth为并网功率。BESS通过储能并网逆变器接入电网，风电功率经过储能系统平滑得到较为平滑的并网功率，从而增加风电并网的可靠性[12]。

图4 基于BESS的风力发电系统Fig.4 Wind power generation system with BESS

2.2 基于模糊变阶EMD滤波的风电功率平滑

利用EMD滤波，将低频信号作为风电功率期望值，高频信号作为储能电池吸收功率期望值，可有效实现平滑风电功率输出。本文提出一种基于模糊控制的方法，自适应调节EMD滤波阶数的平滑功率方法，可以有效地平抑风电功率波动，并且较好地维持储能电池荷电状态的稳定。

图5为储能系统的控制策略。Pr为平抑后输出功率。风电功率进行EMD分解，得到一系列固有模态函数和余量。基于分解结果，将平滑波动率、储能电池SOC作为模糊控制的输入，EMD滤波阶数为输出。根据滤波阶数，通过模糊自适应控制器，确定下一时刻的平滑输出结果[13]。

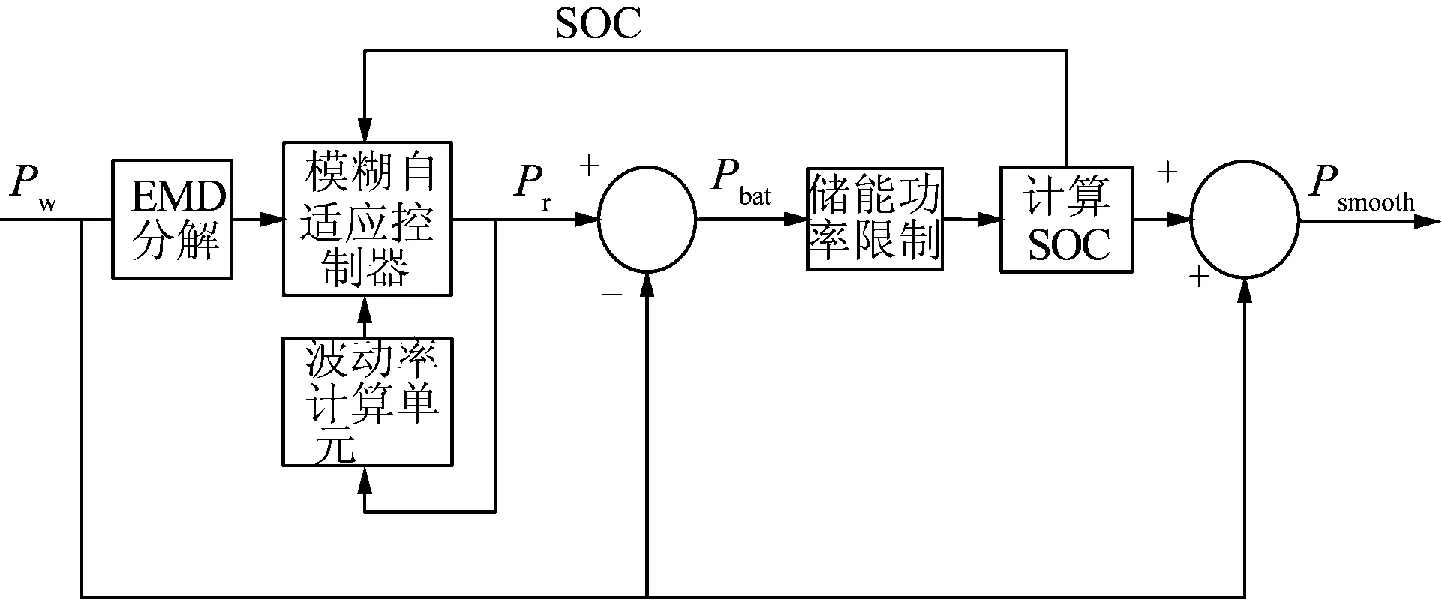
图5 储能系统控制策略Fig.5 Control strategy of BESS

EMD滤波阶次调整策略如下。

储能系统荷电状态是衡量储能系统是否正常运行的重要参数，荷电状态计算公式为

CSOC,t=CSOC,t-Δt+PbatΔt/Cbat

(4)

式中：Cbat为所配置的储能系统额定容量；Δt为采样时间间隔；CSOC初始值为0.5。本文将BESS的SOC划分为3个层次，分别为高、中、低。当SOC偏高时，若处在充电状态下，则选择较低的滤波阶数，防止蓄电池储能系统出现过度充电的状况；若处在放电状态下，则选择较高的滤波阶数，从而相对增大电池储能系统的放电功率，加速其荷电状态的降低，使之向着适中的荷电状态变化，反之亦然。

平抑风电发电波动的主要目的是限制风电场输出功率的变化率，本文的风电波动率计算公式为

(5)

式中：δ为10 min波动率；Pmax为10 min内风电平滑最大出力；Pmin为10 min内风电平滑最小出力；Ccap为风电场开机容量。将平滑波动率划分为3个层次，分别为波动率大、中、小。当风电波动大的时候，则加大储能平滑风电功率的力度，选择较高的滤波阶数，以达到尽可能减缓风电波动的目的；当风电波动小的时候，不需要大力平滑时，则选择较小的滤波阶数，减小储能平滑风电功率出力，节约能源。

图6为储能系统的控制流程图。其中T为对应需要平滑输出个数；t为当前采样点。

2.3 模糊控制器的设计

模糊控制器的作用就是根据平滑后波动率、电池的荷电状态以及储能电池充放电状态得出合适的滤波阶数，从而实时动态平抑风电输出功率，维持储能系统荷电状态在正常工作区间，调节风电波动率大小[14-15]。

本文设计的模糊控制器具有双输入和单输出。2个输入分别为平滑后功率波动率和电池的荷电状态，输出为滤波阶数值。

控制器的输入和输出必须经过模糊化后才能进行模糊推理运算，因此需首先建立输入和输出的模糊集和对应的隶属度函数。模糊控制器的输入模糊化过程所采用的隶属度函数是常用的联合高斯型隶属函数和Sigmoid型隶属函数。

本文中，平滑波动率采用模糊子集{NB,ZO,PB}分别表示当前风电系统的波动情况为{偏低，适中，偏高}。横坐标为平滑波动率，范围为0～0.4。纵坐标为隶属度。储能电池荷电状态采用模糊子集{NB,ZO,PB}表示当前储能系统荷电状态值为{偏低，适中，偏高}。横坐标为SOC值，纵坐标为隶属度。输入量的隶属度函数如图7、8所示。

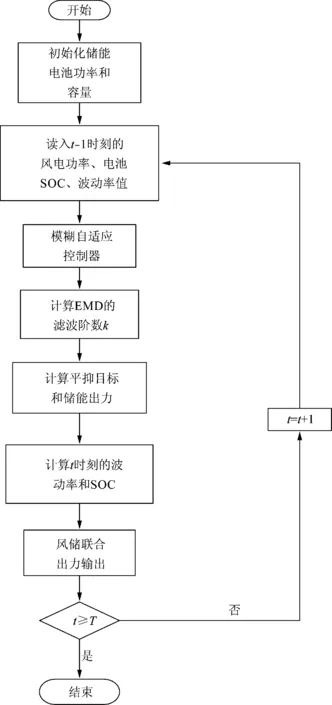
图6 储能系统控制流程图Fig.6 Control flow chart of BESS

图7 平滑后功率波动率隶属度函数Fig.7 Membership functions of power fluctuation rate after smoothing

该模糊控制的模糊推理与去模糊化过程采用Takagi-Sugeno型模糊推理系统使模糊推理与去模糊化相结合。输出值为EMD滤波器的阶次k，为防止滤波器阶次动作过于频繁，本文将模糊控制器输出的滤波阶次进一步化简为3个值，分别为k-1、k和k+1。当模糊控制器的输出取整后，滤波阶次大于k时，

图8 SOC隶属度函数Fig.8 Member functions of SOC

其取整为k+1；当模糊控制器输出取整后，滤波阶次小于k时，其取值为k-1；当模糊控制器输出取整后，滤波阶次等于k时，其值取k。其中k是对风电功率数据进行EMD分解并计算其标准化模量累积均值得出的滤波阶数基准值，计算公式为

(6)

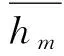
3 仿真分析

以某装机容量为49.5 MW的风电场2011年某日的实际运行数据为例，采样间隔为Δt=1 min，T为1 440，采用储能系统平抑其输出功率波动。本文设定的风储平滑波动率的最大目标波动率为10%。张北国家风光储输示范项目一期工程为100 MW风电配置20 MW的储能系统，参考该示范项目的配置比例，设定仿真中储能系统的额定功率为10 MW。本文研究平抑风电短时功率波动，设定储能系统的额定时间为1 h，即储能系统额定容量为10 MW·h。对风电功率数据进行EMD分解并计算其标准化模量累积均值。第5阶IMF分量开始偏离0，因此，k=5。

图9为平抑前后风电场并网功率曲线。从图9可得，采用模糊变阶EMD平滑后的风储联合输出功率能够很好地跟踪平抑前的风电功率变化趋势。图10为储能系统输出功率。图10展示通过储能系统的及时充放电，有效保证了图9中风储平滑后功率的平抑效果。图11为风电功率原始波动率。从图11中可以看出，原始的风电波动率较大，大于10%的波动率占15.9%。图12为采用模糊变阶EMD平滑波动率，波动率很好地控制在10%以内，这表明本文提出的方案可以有效平抑风电功率波动。

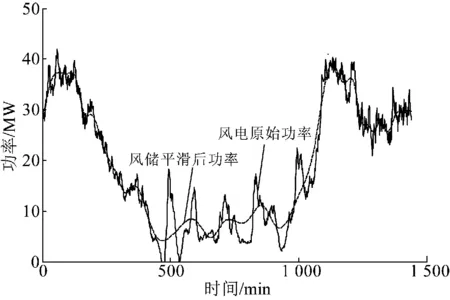
图9 平抑前后风电场并网功率曲线Fig.9 Grid-connected power curve of wind farm before and after smoothing

图10 储能系统输出功率曲线Fig.10 Power output curve of of BESS

图11 风电原始波动率曲线Fig.11 Original fluctuation rate curve of wind power

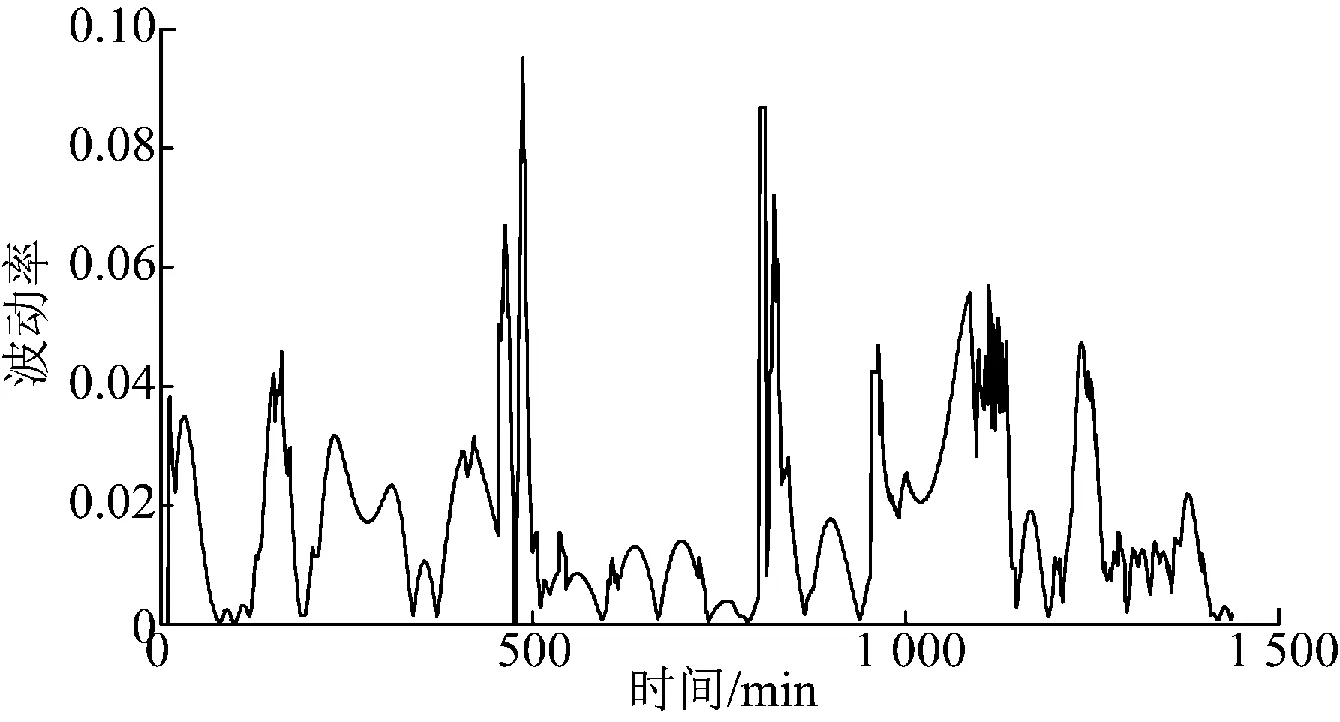
图12 采用模糊变阶EMD平滑波动率曲线Fig.12 Fluctuation rate curve with changing orders of fuzzy EMD filter

为进一步检验本文提出的方案的有效性，与仅考虑储能SOC值变阶EMD的平滑方法进行了仿真对比。仅考虑储能SOC值变阶EMD方法的变阶原则为：当SOC值>0.7且处于充电状态时或者当SOC值<0.3且处于放电状态时，滤波阶次取k-1；当SOC值>0.7且处于放电状态时或者当SOC值<0.3且处于充电状态时，滤波阶次取k+1；其他情况，滤波阶次取k=5。储能SOC值约束上限为0.8，下限为0.2。图13给出了储能SOC值变阶EMD的波动率。可以看出大于10%的波动率占5%，储能SOC值变阶EMD的平滑方法是以降低波动率指标为代价提高储能电池寿命。而本文提出的控制策略，由于采用波动率和SOC为综合约束条件下的模糊变阶，其波动率全部控制在10%以内。

图13 采用SOC约束变阶EMD平滑方法的波动率曲线Fig.13 Fluctuation rate curve with changing orders of EMD filter using SOC constraints

图14为分别采用储能SOC值变阶EMD平滑和模糊变阶EMD平滑2种方法时，SOC值的仿真对比。在储能容量配置固定的情况下，分别采用基于SOC约束变阶EMD平滑方法以及模糊变阶EMD平滑方法计算SOC值的变化情况。

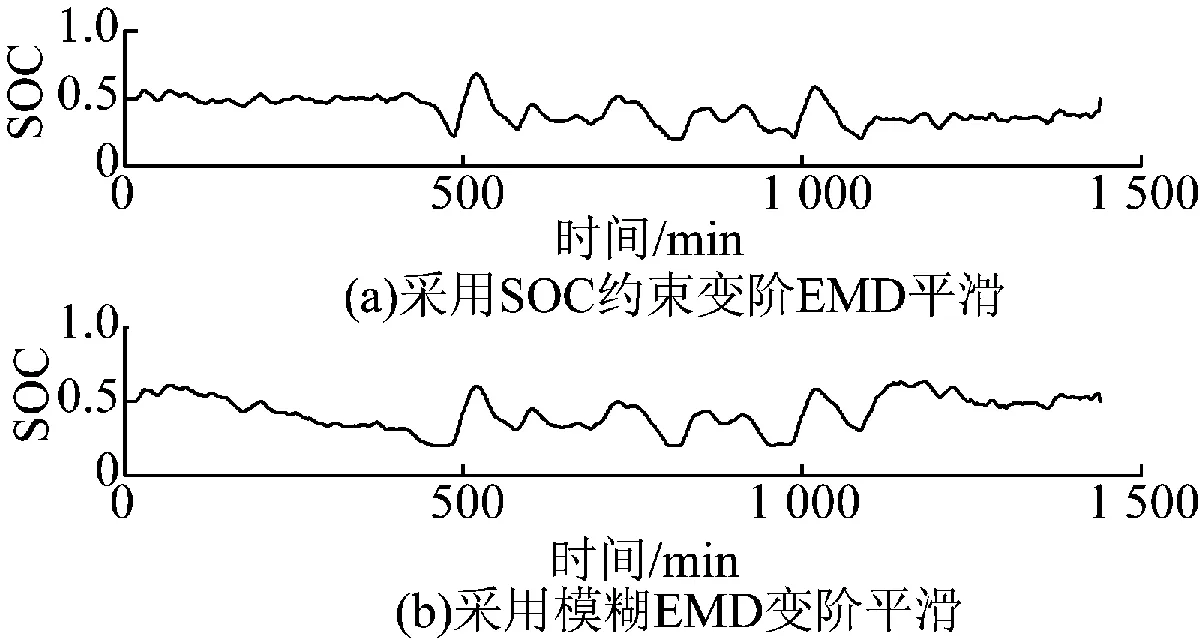
图14 两种平滑方法SOC值对比Fig.14 SOC value comparison betwwen two smoothing methods

由图14可以看出，基于SOC约束变阶EMD平滑方法以及模糊变阶EMD平滑方法，均可以使电池的SOC值稳定在0.2～0.8之间。但基于SOC约束变阶EMD平滑方法，在750 min到1 100 min的时间范围内，SOC值虽然稳定在0.2～0.8之间，但对应图13的波动率，可以看出其波动率大于10%，即基于SOC约束变阶EMD平滑方法是以增大波动率来换取SOC值的良好指标。而本文提出的模糊变阶EMD平滑控制策略，由于考虑了SOC和波动率综合约束变阶，可使SOC和波动率指标同时达到较优，即保证SOC稳定在0.2～0.8，同时波动率限制在10%以内。

4 结 论

本文提出了一种平抑风电功率波动的方法，基于模糊经验模态分解，将风电功率信号分解成低频信号和高频信号。将低频信号作为风电场的并网功率；高频信号由储能电池吸收，以平抑风电功率波动。为较好地平滑风电波动率并且稳定储能荷电状态，将平滑后波动率和储能电池荷电状态作为约束条件，采用模糊自适应控制的方法，调节EMD滤波阶数以平滑风电输出。仿真分析验证了本文所提控制策略的有效性。与采用SOC约束变阶方法进行比较，平滑波动效果更好，可以将波动率控制在10%以内，减小了风电波动给电网带来的影响，同时可以稳定储能电池SOC，实现储能系统性能指标和波动率指标的协调优化。

[1]中国电力科学研究院.风电场接入电力系统技术规定：GB/T 19963—2011 [S].北京：中国标准出版社，2012.

[2]程时杰，文劲宇，孙海顺. 储能技术及其在现代电力系统中的应用[J].电气应用，2005，24(4)：1-6.

[3]张文亮，丘明，来小康. 储能技术在电力系统中的应用[J].电网技术，2008，32(7)：1-9. ZHANG Wenliang，QIU Ming，LAI Xiaokang. Application of energy storage technologies in power grids[J] .Power System Technology，2008，32(7)：1-9.

[4]谢俊文，陆继明，毛承雄，等.基于变平滑时间常数的电池储能系统优化控制方法[J]. 电力系统自动化，2013，37(1)：96-102. XIE Junwen，LU Jiming，MAO Chengxiong，et al. Optimal control of battery energy storage system based on variable smoothing time constant[J]. Automation of Electric Power System，2013，37(1)：96-102.

[5]BREKKEN T K A，YOKOCHI A，VON JOUANNE A，et al. Optimal energy storage sizing and control for wind power applications[J]. IEEE Transactions on Sustainable Energy，2011，2(1)：69-77.

[6]ESMAILI A, NOVAKOVIC B, NASIRI A, et al. A hybrid system of Li-Ion capacitors and flow battery for dynamic wind energy support[J]. IEEE Transactions on Industry Applications, 2013, 49(4): 1649-1657.

[7]张野，郭力，贾宏杰，等. 基于电池荷电状态和可变滤波时间常数的储能控制方法[J]. 电力系统自动化，2012，36(6)：34-38, 62. ZHANG Ye，GUO Li，JIA Hongjie，et al.An energy management method of hybrid energy storage system based on smoothing control[J].Automation of Electric Power Systems，2012，36(6)：34-38, 62.

[8]张坤，吴建东，毛承雄，等. 基于模糊算法的风电储能系统的优化控制[J].电工技术学报，2012，27(10)：235-241. ZHANG Kun, WU Jiandong, MAO Chengxiong，et al.Optimal control of energy storage system for wind power generation based on fuzzy algorithm [J].Transactions of China Electrotechnical Society, 2012，27(10)：235-241.

[9]孟顺，谢桦. 基于经验模态分解的平滑可再生能源功率波动的储能容量优化[J]. 电源学报，2014，5(5)：7-11, 18. MENG Shun，XIE Hua. Energy storage capacity optimization in smoothing renewable energy power fluctuation based on empirical mode decomposition[J]. Journal of Power Supply，2014，5(5)：7-11, 18.

[10]韩晓娟，陈跃燕，张浩, 等，基于小波包分解的混合储能技术在平抑风电场功率波动中的应用[J].中国电机工程学报，2013，33(19)：8-13 HAN Xiaojuan，CHEN Yueyan，et al. Application of hybrid energy storage technology based on wavelet packet decomposition in smoothing the fluctuations of wind power [J]. Proceedings of the CSEE，2013，33(19)：8-13.

[11]孙晖.经验模态分解理论与应用研究[D].杭州：浙江大学，2005. SUN Hui. Research on empirical mode decomposition theory and its application[D]. Hangzhou：Zhejiang University，2005.

[12]FLANDRIN P, RILLING G, GONCALVES P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters, 2004, 11(2): 112-114.

[13]张步涵，曾杰，毛承雄，等. 电池储能系统在改善并网风电场电能质量和稳定性中的应用[J].电网技术，2006，30(15)：54-58. ZHANG Buhan，ZENG Jie，MAO Chengxiong，et al. Improvement of power quality and stability of wind farms connected to power grid by battery energy storage system[J]. Power System Technology. 2006，30(15)：54-58. [14]吴振威，蒋小平，马会萌，等. 用于混合储能平抑光伏波动的小波包-模糊控制[J]. 中国电机工程学报，2014，34(3)：317-324. WU Zhenwei，JIANG Xiaoping，MA Huimeng，et al. Wavelet packet-fuzzy control of hybrid energy storage systems for PV power smoothing[J]. Proceedings of the CSEE，2014，34(3)：317-324.

[15]LI X. Fuzzy adaptive Kalman filter for wind power output smoothing with battery energy storage system[J]. IET Renewable Power Generation，2012，6(5)：340-347.

(编辑 景贺峰)

Control Strategy of Smoothing Wind Power Output Using Battery Energy Storage System Based on Fuzzy Empirical Mode Decomposition

YANG Xiyun1, CAO Chao2, LI Xiangjun3, REN Jie1, GAO Feng1, WU Zihan1

(1.School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China; 2.Central Research Institute of Shanghai Electric Group Co. Ltd, Shanghai 200070, China; 3.China Electrical Power Research Institute, Beijing 100192, China)

To reduce the fluctuation rate of wind power and improve the reliability of grid, this paper proposes a control method of smoothing wind power output with battery energy storage system based on fuzzy empirical mode decomposition (EMD). Wind power is decomposed by EMD into two parts, the low-frequency part is used as wind power grid-connected value and the high-frequency part is stored by battery energy storage system (BESS). Taking the fluctuation rate of wind power output after smoothing and the state of charge (SOC) as constraints, the orders of EMD filter can be adaptively adjusted on-line based on fuzzy control method, which can smooth wind power fluctuation better through fuzzy adaptive controller. Compared with another energy storage system control strategies for smoothing wind power, the simulation results show that the proposed method can effectively smooth the fluctuation of winds power output and avoid the over-charging and over-discharging of energy storage system so as to keep SOC stable.

empirical mode decomposition (EMD); power smoothing; fuzzy control method; fluctuation rate; state of charge (SOC)

中央高校基本科研业务费专项资金资助项目(2015MS32)；北京市自然科学基金项目(4132061)；北京市科技新星计划项目(Z141101001814094)；国家电网公司科技项目(DG71-14-046)

TM 71

A

1000-7229(2016)08-0134-07

10.3969/j.issn.1000-7229.2016.08.021

2016-04-29

杨锡运(1973)，女，博士，教授，主要研究方向为新能源发电技术；

曹超(1990)，男，硕士研究生，主要研究方向为新能源发电控制技术和储能技术；

李相俊(1979)，男，博士，教授级高级工程师，主要研究方向为大规模储能技术、新能源与分布式发电及电力系统分析；

任杰(1992)，男，硕士研究生，主要研究方向为新能源发电控制技术和储能技术；

高峰(1976)，男，博士，讲师，主要研究方向为新能源发电技术；

吴子晗(1990)，男，硕士研究生，主要研究方向为新能源发电技术。

Project supported by Fundamental Research Funds for the Central Universities(2015MS32)； Beijing Natural Science Foundation (4132061); Beijing New-star Plan of Science and Technology (Z141101001814094); Science and Technology Project of SGCC(DG71-14-046)