时滞对风储平滑功率效果的影响分析

赵昱杰，凌志斌，张敏吉

(1.上海交通大学电气工程系，上海市 200240；2.中海油研究总院新能源研究中心，北京市 100015)

时滞对风储平滑功率效果的影响分析

赵昱杰1，凌志斌1，张敏吉2

(1.上海交通大学电气工程系，上海市 200240；2.中海油研究总院新能源研究中心，北京市 100015)

风储配合是平抑风功率波动的有效途径，时滞给风储系统控制策略的运行效果带来了不利的影响。分析了风储系统各环节的时滞对功率平滑策略产生的影响，并提出了增加系统指令更新周期的解决方法，在Matlab/Simulink平台中对该方法进行仿真，分析了不同的系统指令更新周期对风储系统风功率平抑控制策略运行效果的影响。仿真结果表明，系统指令更新周期为系统平均时延的2倍时，可以保证平抑风功率控制策略的有效实现。将该结论应用于实际风储系统中进行论证，仿真结果和实际风储系统运行情况均表明了该方法的有效性，可以为风储系统平滑功率等相应策略的设计提供参考。

风储系统；风功率波动；风功率平滑；时滞

0 引 言

随着全球能源和环境问题的日益突出，风能作为一种清洁的可再生能源，越来越受到世界各国的重视。然而，随着并网风电场规模的不断扩大，风功率的波动性和间歇性对其接入电网带来的不利影响也愈发显著，使得大规模风电接入电网的能力受到限制。储能系统[1]可以适时吸收释放功率，为平抑风电功率波动，提高风电接入电网的能力提供了有效的手段[2]。大容量储能通过发出/吸收的有功功率和无功功率与风电机组的输出配合，实现对风电平滑风电功率、削峰填谷、无功补偿、无功调压、有功调频和计划跟踪的作用[3-4]。实现不同的作用，对储能系统的响应能力提出的要求也不同。其中削峰填谷和计划跟踪对响应能力要求较低，数十s即可满足需求；平滑功率、无功补偿、无功调压和有功调频对响应能力要求稍高，响应时间不大于1 s[5]。

在风储系统控制策略中，平滑功率控制策略可以有效降低风电场功率的波动性[6]，降低电网调频压力，提高电网接入风电的能力，已经成为主要的应用方向之一。目前常用的波动平抑控制算法有一阶滤波控制算法、卡尔曼滤波算法、小波滤波等。但是，上述算法主要是基于理论分析和仿真分析2种途径[7]，而没有考虑实际情况下风储系统的时滞特性对控制算法的影响。

风储系统各环节均不同程度地存在响应延迟，延迟响应使得整个系统具有显著的时滞特性。时滞特性对系统控制策略的运行效果造成了巨大的影响[8-9]，系统的时滞特性使得系统的功率平滑等控制策略的运行性能严重下降，甚至无法实现其功能。理想情况下的控制策略需要根据实际情况进行重新设计和评估。

本文以一阶滤波平滑功率控制算法在风储协调系统中的应用为背景，分析时滞对控制算法运行效果的影响，并针对影响对算法在应用中进行改进。改进后的算法能够应用于带时滞的风储系统，使之实现风功率平抑的功能。

1 风功率波动情况与要求

1.1 风功率实际波动情况

风功率具有随机性和波动性。图1为2013年5月29日内蒙古某风场中一台风机的日功率曲线。

图1 2013年5月29日功率曲线Fig.1 Power curve on May 29, 2013

由图1可以看出，风速具有的随机性使得风电功率波动性很大，因此有必要通过与储能系统配合，平抑风电功率波动，降低风电功率波动对电网的影响。

1.2 国标对风功率波动要求

风电出力的短时随机波动会对电网调频带来不良影响，风电功率的大幅度波动可能使电网失去稳定。各个国家对风电并网都提出了相关技术要求，但要求各异[10]。根据我国国家标准《GB/T 19963—2011风电场接入电力系统技术规定》[11]，要求风电场具有有功功率调节能力，并能根据电网调度部门指令控制其有功功率输出，并对输出功率的变化率进行了限制，标准中的风电场有功功率变化限值推荐如表1所示。

2 功率平滑控制改善方法

2.1 风功率平滑策略

风功率平滑策略有多种[12-15]，最常见的是采用一阶低通滤波原理对风电功率高频波动分量进行滤除[16]。

表1 风电场容量与输出功率变化率限制值
Table 1 Wind farm capacity and limit of output power change rate

(1)

式中：τ为滤波时间常数，且τ=1/(2πfc)，fc为对应的低通滤波截止频率；Pwind,t和Pout,t分别为t时刻风电功率滤波前和滤波后的功率；Δt为风电功率的采样周期。由公式(1)可得经滤波后风电功率为

(2)

由公式(2)可知，当τ= 0时，有Pout,t=Pwind,t，即此时对风电功率无滤波作用。当τ越大时，Pout,t越接近Pout,t-Δt，即输出功率曲线越平滑，对风电的滤波作用越明显。

2.2 风储系统模型

风储系统由风机、电池组、能量管理系统(energy manage system，EMS)、电池管理系统(battery manage system，BMS)和能量转换系统(power convert system，PCS)组成，如图2所示。

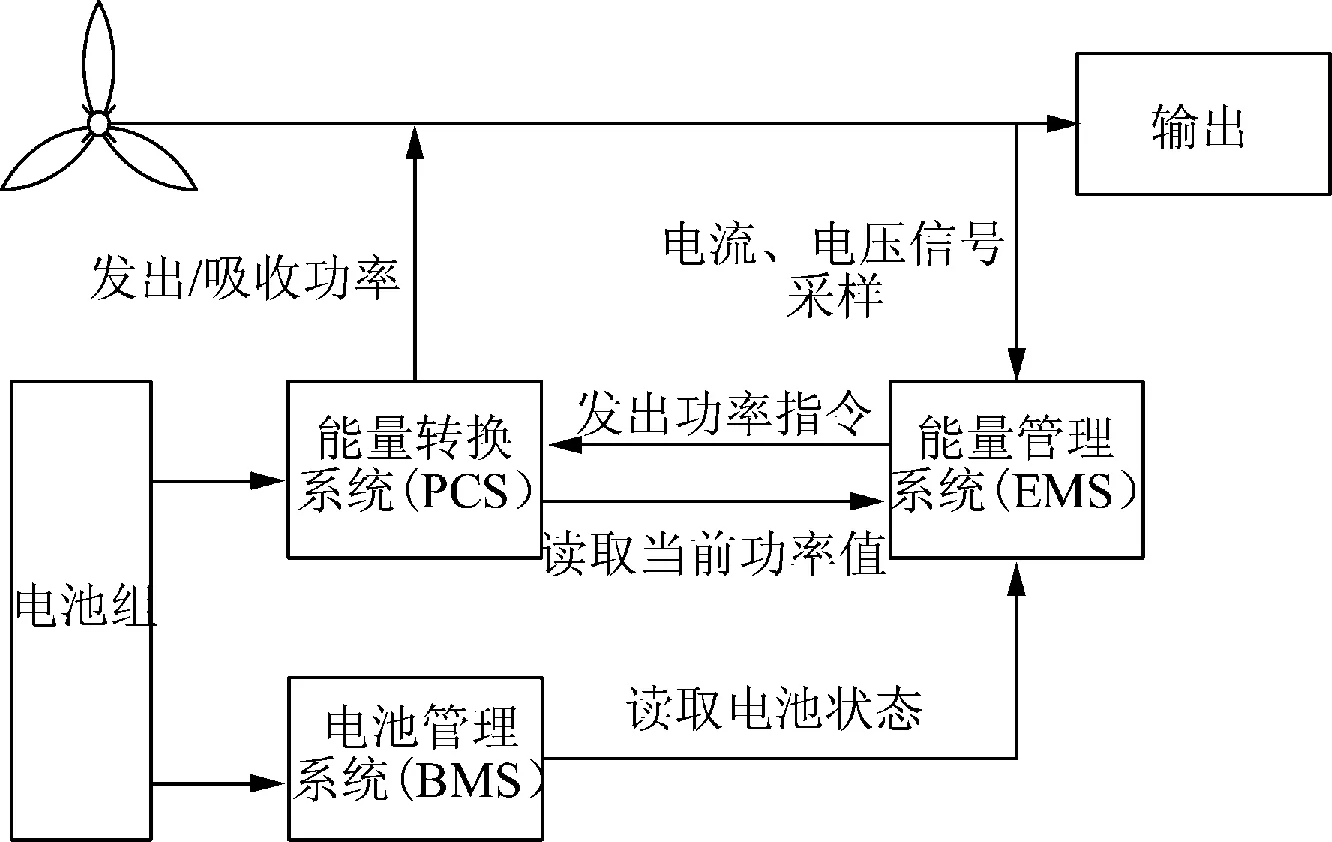
图2 风储能系统示意图Fig.2 Schematic diagram of wind energy storage system

EMS通过对输出电流、电压值的采集计算出系统输出总功率Pout，其中总功率为风机输出功率和PCS输出功率的总和。同时EMS通过通讯读取PCS的功率值PPCS得出风机的输出功率Pwind，其中Pwind=Pout-PPCS。

2.2.1 理想情况下风储功率平滑模型

风储系统的功率平滑理想模型如图3所示。设在t时刻EMS获得的系统数据有当前时刻风功率Pwind,t和前一时刻风储系统实际输出总功率Pout,t-Δt，根据公式(2)计算出当前时刻的理想输出功率值Pout,t，将理想输出功率值Pout,t与当前风功率Pwind,t相减即得出PCS功率指令，EMS将功率指令发送至PCS使其发出/吸收相应的功率PPCS,t。

图3 风储系统平滑功率理想模型Fig.3 Ideal model of smoothing power for wind storage system

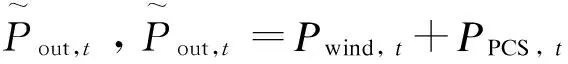
2.2.2 实际情况下风储功率平滑模型

风储系统功率平滑控制策略的理想实现，是建立在t时刻EMS发出的功率指令P1t、PCS实际发出/吸收的功率值P2t、EMS读取的PCS功率值P3t相等的条件之上，即P1t=P2t=P3t。

但在实际情况中，风储系统多个环节均有延时，EMS将指令发送至PCS所需时间为T1，PCS收到EMS指令并开始执行所需要的时间为T2，PCS将当前功率值发送给EMS所需的时间为T3，得到风储系统的实际控制框图如图4所示。

图4 风储系统平滑功率实际控制框图Fig.4 Actual control block diagram of smoothing power of wind power storage system

令τ1为从EMS发出功率指令给PCS，到PCS接收功率指令并开始执行的延时时间，τ1=T1+T2。τ2为从EMS发出功率读取指令到PCS，到EMS读取到PCS当前功率值的延时时间，τ2=T1+T3。

由于系统的时滞性，设在任意时刻t，EMS发出的功率指令P1t=PPCS,t，PCS当前实际发出/吸收的功率值P2t=PPCS,t-τ1，EMS读取PCS功率值P3t=PPCS,t-τ1-τ2是不相等的，即P1t≠P2t≠P3t。

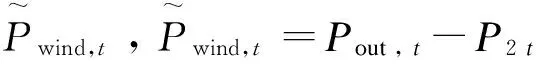
由于计算得出的风功率值与实际的风功率不相等，因此对计算出的风功率值进行滤波计算而得出的PCS功率指令也与理想的功率指令不相等，导致PCS发出的功率与风功率叠加后与理想的输出功率值不相等，系统的功率平滑控制策略就会失效。

2.2.3 带时滞的风储系统平滑控制效果仿真分析

在Matlab/Simulink平台上对带时滞的风储系统进行仿真分析，分析所用数据来源为2013年5月17日内蒙古某风电场其中一台风机的实测数据，数据采样周期为0.25s。在模型中EMS发出功率指令到PCS开始执行的时延τ1=500ms，EMS发出读取功率指令到接收PCS返回当前的功率值的时延τ2=450ms。PCS额定输出功率为500kW，即功率限幅为±500kW，平滑策略采用的低通滤波时间常数为 10min。图5和图6分别表示了风功率曲线、不考虑时滞的风储系统输出曲线和考虑时滞的风储系统输出曲线。

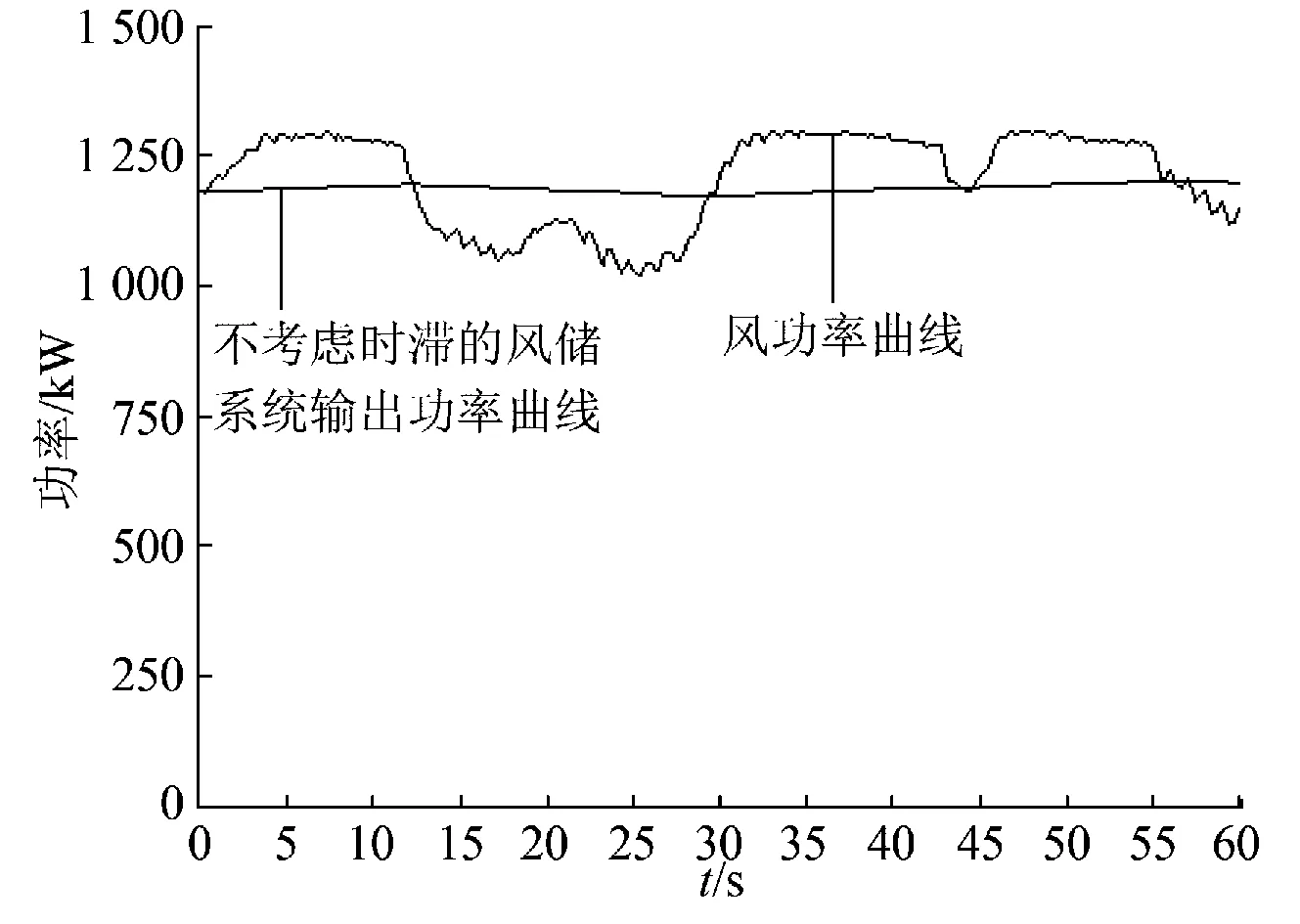
图5 风功率曲线和理想输出功率曲线Fig.5 Wind power curve and ideal output power curve

图5表明在理想状态下，风储系统的平滑功率策略能起到很好的效果，但是在存在时滞的系统中，系统输出功率如图6所示，时滞对系统平滑功率策略的运行造成了很大的影响，系统运行至第5 s的时候平滑功率策略已经失效。

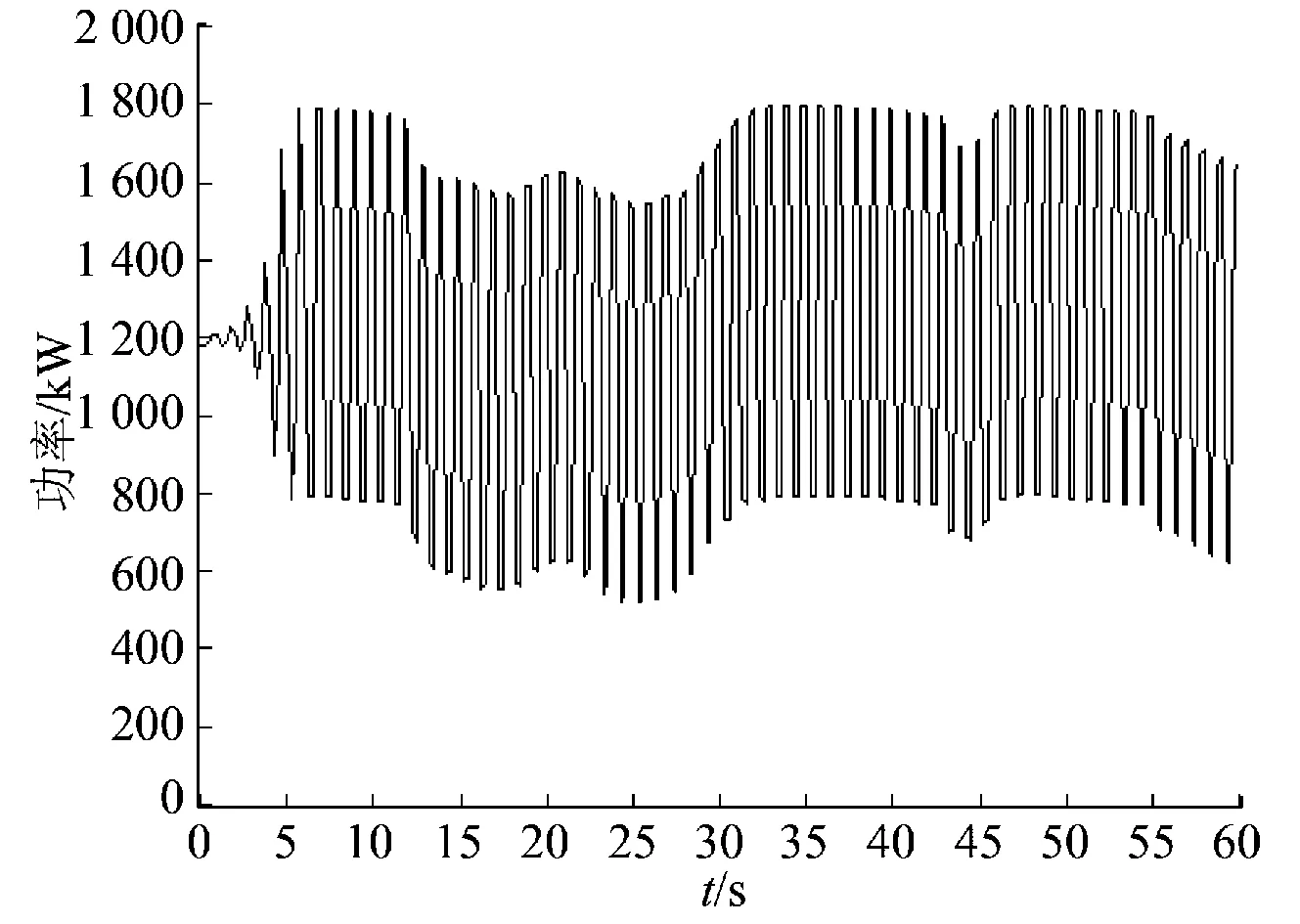
图6 带时滞的风储系统输出功率曲线Fig.6 Output power curve of wind power storage system with time delay

3 原因分析及改善措施

3.1 带时滞的风储系统功率平滑策略分析

根据以上的分析，在带有时滞的风储系统中，系统的平滑功率策略运行不稳定的主要原因为EMS发出的功率指令P1、PCS实际执行的功率值P2、EMS读取的PCS功率值P3三者不相等导致控制运算出现误差引起的，因此可以通过降低系统指令更新速度，即增加系统的指令更新周期来解决该问题。

设系统在kT时刻开始更新指令，其指令值为PPCS,kT，T为系统的指令周期，k=0,1,2…。此时EMS获得的数据有当前时刻系统输出总功率Pout,kT、上一系统指令周期中EMS发送给PCS的功率指令PPCS,(k-1)T、以及读取到的当前PCS的功率值PPCS,kT-t1-t2，令T>t1+t2。对于任意的时刻t，在kT≤t≤(k+1)T的时间范围内，EMS发出的功率指令不变，因此其PCS的功率值也是恒定不变的。因此，在系统更新指令的时刻kT，有：

P1t=PPCS，(k-1)T

(3)

P2t=PPCS,kT-τ1

(4)

P3t=PPCS,kT-τ1-τ2

(5)

P1t=P2t=P3t

(6)

即实现了EMS发出的功率指令值、PCS执行的功率指令值和EMS读取的PCS功率值三者相等。

将上述系统进行离散化分析，增加系统指令更新时间可以等效为增加系统采样周期，在S域中分析得出的输入输出表达式为

(7)

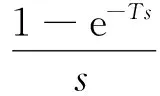
(8)

(9)

由公式(9)可得，不能从系统离散化公式中获得系统传递函数的表达式，可以从数字仿真的角度进行分析。

3.2 带时滞的风储系统指令更换周期仿真分析

图7为系统指令更新周期为1 s的功率曲线图。由图7可以看出，仿真系统输出功率曲线围绕着理想输出功率曲线波动，与风机输出功率曲线相比，其波动性有很大的减少，风功率的波动得到了很大的平滑，风储系统的平滑功率策略取得了效果。

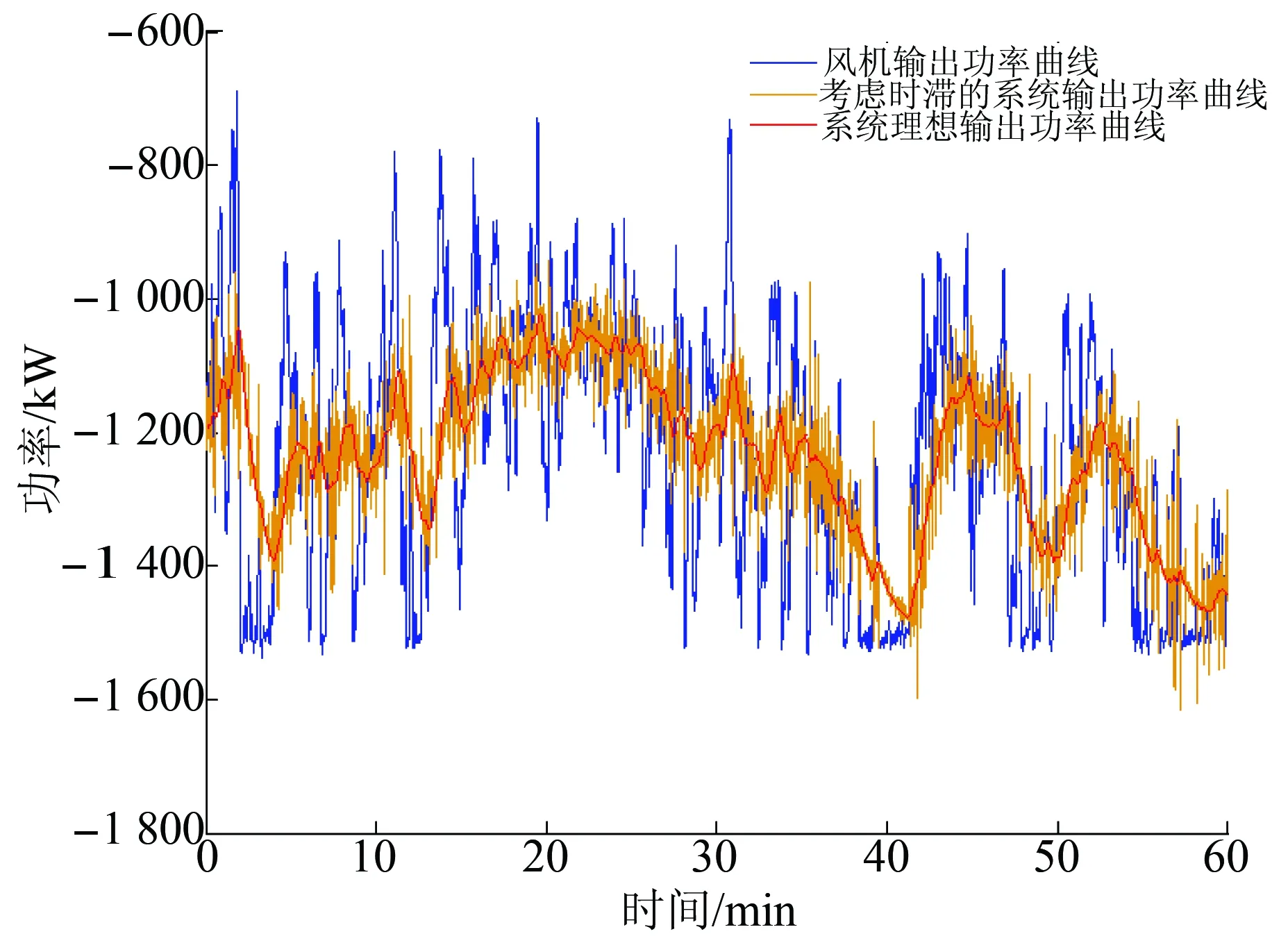
图7 系统指令更新周期为1 s的功率曲线图Fig.7 Power curve with 1 s periodic updating system instruction

在实际情况下，系统的延迟时间也具有一定的时变性，为了保证系统的稳定运行，应当使系统的指令更新周期时间足够长，使得T≥max(τ1+τ2)。图8为系统指令更新周期为2 s时得到的平滑功率曲线图。对比图7、8可以看出，随着系统指令更新周期的增加，系统实际输出功率曲线波动变大，风功率平抑效果变差，因此系统指令更新周期的选择必须在保证系统稳定性的前提下尽可能小。

可以通过比较系统实际输出功率与理想输出的差异，来分析不同系统指令更新周期对风储功率平滑策略的影响。设Pt为t时刻系统理想输出功率曲线的功率值，PT,t为系统指令更换周期为T时t时刻系统实际输出功率曲线的功率值。

图8 系统指令更新周期为2 s的功率曲线图Fig.8 Power curve with 2 s periodic updating system instruction

图9 系统指令更新周期与系统输出功率平均误差关系图Fig.9 Relationship between system instruction update cycle and system output power average error

从图9中可以看出，可以将系统的指令更新周期设计为2 s，T≈2(τ1+τ2)，其输出功率的平均误差约为20 kW，为风机当天实际最大功率的1.39%，这样既可以保证系统的稳定运行，也保证了较好的风功率平抑效果。

3.3 带时滞的风储系统指令更新周期测试验证

本文于2015年6月在内蒙古某风电场的风储系统进行了功能测试，为了使风储系统平滑功率策略能够稳定实现，必须对系统的指令周期进行选择，图10和图11分别为系统指令更新周期为 1 s和2 s的系统功率曲线。

图10 系统指令更新周期为1 s时系统功率曲线Fig.10 System power curve with 1 s periodic updating system instructions

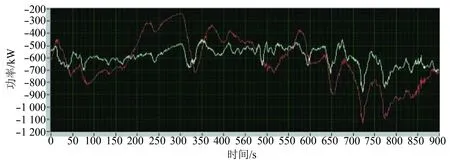
图11 系统指令更新周期为2 s时系统功率曲线Fig.11 Power curve with 2 s periodic updating system instructions

在图10中，红色曲线为风机发出的功率曲线，白色曲线为经过平滑策略后风储系统发出的总功率曲线。由图10可以看出，系统更新周期取1 s时，风功率的波动幅值虽然有所减少，但是风功率平抑效果并不明显，这是由于系统时延的动态波动使得PCS功率指令执行时间T

在图11中，红色曲线为风机输出功率曲线，白色曲线为经过平滑策略后风储系统发出的总功率曲线。由图10和图11可以看出，当系统指令更新周期为 1 s时，由于系统时延最大值大于系统指令更新周期，因此风功率平抑效果不明显。当指令更换周期为2 s时，系统平滑功率策略运行稳定，因此，风储系统指令更换周期确定为2 s，即T≈2(τ1+τ2)。这与3.2节仿真所得的结论是相吻合的。

4 结 论

通过理论分析、仿真和实际验证可得出以下结论。

系统的时滞特性可能引起风储系统平滑功率策略的失效。增加系统的指令更新周期，使其大于系统控制环路最大的整体延迟时间，可以保证系统平滑功率策略的有效运行。

继续增加系统的指令更新时间，功率平滑策略的运行效果变差，一般可以取指令更新时间为系统控制环路总延迟时间的2倍，既可以保证系统功率平滑策略稳定运行，也保证了良好的风功率平滑效果。

本文的分析主要考虑了1台风机的情况，实际测试验证也是在“一机一储”的风储结构上进行的。对于分布式的“一机一储”配置结构，本文结论能够很好应用于多台风机同时运行的情况。对于集中式的“多机一储”或“一场一储”的风储配置，只要控制系统数学模型与本文分布式“一机一储”相同，本文结论同样适用。本文结论可为相关系统的运行设计提供参考。

[1]许守平,李相俊,惠东. 大规模储能系统发展现状及示范应用综述[J]. 电网与清洁能源,2013,29(8):94-100, 108. XU Shouping,LI Xiangjun,HUI Dong. A survey of the development and demonstration application of large-scale energy storage[J]. Power System and Clean Energy, 2013,29(8):94-100, 108.

[2]李文斌. 储能系统平抑风电场功率波动研究[D].重庆: 重庆大学,2012. LI Wenbin. Study on the smooth up wind farm output fluctuation by energy storage system[D]. Chongqing: Chongqing University,2012.

[3]高明杰,惠东,高宗和,等. 国家风光储输示范工程介绍及其典型运行模式分析[J]. 电力系统自动化,2013,37(1):59-64. GAO Mingjie,HUI Dong,GAO Zonghe, et al. Presentation of national wind/photovoltaic/energy storage and transmission demonstration project and analysis of typical operation modes[J]. Automation of Electric Power Systems, 2013,37(1):59-64.

[4]苗福丰,唐西胜,齐智平. 风储联合调频下的电力系统频率特性分析[J], 高电压技术, 2015, 41(7): 2209-2216. MIAO Fufeng,TANG Xisheng,QI Zhiping. Analysis of frequency characteristics of power system based on windfarm-energy storage combined frequency regulation[J]. High Voltage Engineering, 2015, 41(7): 2209-2216.

[5]朱琳. 含风电场的电力系统频率紧急控制措施研究[D].北京: 华北电力大学,2012. ZHU Lin. Research on the emergency frequency control measures for power system with wind farms integration[D]. Beijing: North China Electric Power University,2012.

[6]陈芳. 风储系统功率平滑控制策略研究[D].北京: 华北电力大学,2013. CHEN Fang. A control strategy to smooth the fluctuation of wind power based on wind power and energy storage system[D]. Beijing: North China Electric Power University, 2013.

[7]汪海蛟,江全元. 应用于平抑风电功率波动的储能系统控制与配置综述[J]. 电力系统自动化,2014, 38(19):126-135. WANG Haijiao, JIANG Quanyuan. An overview of control and configuration of energy storage system used for wind power fluctuation mitigation[J]. Automation of Electric Power Systems, 2014, 38(19):126-135.

[8]王居凤. 具有时延的网络控制系统的稳定性[D].无锡: 江南大学,2013. WANG Jufeng. Stability of the networked control systems with time delay[D].Wuxi: Jiangnan University,2013.

[9]由嘉. 网络环境下不确定时滞系统鲁棒滤波问题的研究[D].哈尔滨: 哈尔滨工业大学,2013. YOU Jia. Robust filtering for uncertain systems with time-varying delay in network environment[D]. Harbin: Harbin Institute of Technology,2013.

[10]饶建业,徐小东,何肇,等. 中外风电并网技术规定对比[J]. 电网技术,2012, 36(8):44-49. RAO Jianye,XU Xiaodong,HE Zhao, et al. Comparison on technical regulations of China and other countries for grid-connection of wind farms[J]. Power System Technology,2012, 36(8):44-49.

[11]中国电力科学研究院. 风电场接入电力系统技术规定：GB/T 19963—2011[S]. 北京：中国标准出版社，2012.

[12]胡雪松,孙才新,刘刃,等. 采用飞轮储能的永磁直驱风电机组有功平滑控制策略[J]. 电力系统自动化,2010, 34(13):79-83. HU Xuesong,SUN Caixin, LIU Ren, et al. An active power smoothing strategy for direct-driven permanent magnet synchronous based wind turbine using flywheel energy storage[J]. Automation of Electric Power Systems, 2010, 34(13): 79-83.

[13]洪海生,江全元,严玉婷. 实时平抑风电场功率波动的电池储能系统优化控制方法[J]. 电力系统自动化,2013, 37(1):103-109. HONG Haisheng,JIANG quanyuan,YAN Yuting. An optimization control method ofbattery energy storage system with wind power fluctuations smoothed in real time[J]. Automation of Electric Power Systems, 2013, 37(1): 103-109.

[14]赵瑜,周玮,于芃,等. 风电有功波动功率调节控制研究[J]. 中国电机工程学报,2013, 33(13):85-91. ZHAO Yu,ZHOU Wei,YU Peng, et al. Study on regulation and control of active wind power fluctuations[J]. Proceedings of the CSEE, 2013, 33(13):85-91.

[15] LI X. Fuzzy adaptive Kalman filter for wind power output smoothing with batteryenergy storage system[J].IET Renewable Power Veneration, 2012, 6(5):340-347.

[16]石世前. 风光储联合发电系统中储能设备容量配置与运行策略研究[D].北京: 华北电力大学,2014. SHI Shiqian. Capacity configuration and operation strategy of energy storage devices in hybrid wind/photovoltaic power generation system with energy storage[D]. Beijing: North China Electric Power University,2014.

(编辑 景贺峰)

Effect of Time Delay on Smoothing Power Efficiency of Wind Turbine-Energy Storage System

ZHAO Yujie1, LING Zhibin1, ZHANG Minji2

(1.Department of Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. New Energy Research Center of CNOOC Research Institute, Beijing 100015, China)

Wind storage coordination is the effective way to stabilize wind power fluctuation,and time delay has a negative impact on the operation of the wind storage system’s control strategy. This paper analyzes the impact of the time delay of each section in the wind storage system on power smoothing strategies, and proposes the solution to increase the system instruction update cycle. We simulate the method on the Matlab/Simulink platform, and analyze the impacts of different system instruction update cycles on the running effect of wind power smoothing control strategy of wind storage system. The simulation results show that, when the instruction system update cycle is twice the average time delay of the system, it can guarantee the effective implementation of the wind power smoothing control strategy. We apply the conclusion into the practical wind storage system, and the simulation results and the operation condition of actual wind storage system both show the effectiveness of the method, which can be a reference for the design of the smoothing power and other corresponding strategies of the wind power storage system.

wind storage system; wind power fluctuation; wind power smoothing; time delay

TM 614

A

1000-7229(2016)08-0128-06

10.3969/j.issn.1000-7229.2016.08.020

2016-03-12

赵昱杰(1990)，男，硕士研究生，主要研究方向为风力发电和电池储能；

凌志斌(1976)，男，博士，副教授，主要研究方向为风力发电技术和电池储能技术；

张敏吉(1978)，男，硕士研究生，主要研究方向为太阳能电池、电池储能技术等。