基于双向互补的储能系统控制策略及经济性分析

2017-01-06张婳张斌籍天明韩晓娟

电力建设 2016年8期

张婳，张斌，籍天明，韩晓娟

(1.华北电力大学控制与计算机工程学院，北京市 102206；2. 国网冀北三河市供电有限公司，河北省三河市 065200；3. 南京南瑞集团信息系统集成分公司，南京市 211106)

张婳1，张斌2，籍天明3，韩晓娟1

储能系统成本高、控制技术不成熟，制约了电池储能系统的大规模应用。在充分考虑电池储能系统经济性基础上，该文提出了基于双向互补的储能系统控制策略。由2组电池构成双向互补电池储能系统，通过雨流计数法计算电池充放电深度(depth of discharge, DoD)，以表征电池循环寿命，并建立了双向互补储能系统充放电控制模型。基于国内某光-储联合电站实测数据，在储能系统不同充放电临界荷电状态限定范围内，对双向互补电池储能系统控制策略的经济性进行了仿真分析。仿真结果表明，与单储能系统控制策略相比，基于双向互补的电池储能系统控制策略可以有效提高电池储能系统的使用寿命，降低储能系统成本，具有良好的工程应用前景。

储能系统；双向互补；控制策略；经济性分析

0 引言

随着可再生能源发电装机容量的提高，其输出功率的波动性、间歇性给电力系统的运行带来一定冲击[1-2]。储能系统作为一种具有快速响应和动态调节能力的设备，可以有效改善可再生能源发电的电能品质，提高可再生能源电力系统的友好性[3-4]。然而，由于目前技术水平有限，储能系统多处于示范工程阶段，尚未得到大规模应用[5-6]。主要原因在于现在储能系统的成本很高以及控制技术尚未成熟。因此，使用电池储能系统时应重点关注其经济性，而电池循环寿命是影响电池储能系统经济性的重要因素。

当选定电池类型后，控制策略决定了电池的循环寿命。文献[7]采用低通滤波技术平抑风电功率波动，根据历史风电功率确定储能电池容量和滤波器时间常数。文献[8]根据锂电池储能系统的能量状态，动态调整2个时间尺度的波动限制指标，以缓解储能系统过充/过放的压力。文献[9]提出了基于卡尔曼滤波的储能系统能量状态反馈控制技术，用来实现风电功率平滑。文献[10]提出了基于模型预测控制技术的储能电池平抑风电功率波动方法。文献[11]利用滑动平均滤波算法计算风电输出功率的目标值，使电池储能系统的荷电状态(state of charge, SOC) 稳定在一定的范围内，避免电池储能系统出现过充和过放。

目前大部分有关储能系统控制策略的文献都没有考虑储能系统的经济性。在储能元件单价一定的情况下，储能系统经济性的关键参数是循环使用寿命。在充分考虑储能系统经济性的基础上，本文提出基于双向互补的电池储能系统优化控制策略，采用2组电池组构成双向互补电池储能系统，令2组电池充放电状态相反且同时切换，减小运行周期内电池储能系统的损耗，延长电池储能系统的使用寿命，提高其经济性。

1 光伏功率波动平抑控制及电池寿命计算

1.1 光伏功率波动平抑控制算法

选取储能系统的应用场景为平抑光伏电站功率波动，储能系统为铅酸电池储能系统。某光伏电站装机容量为40 MW，出力时间为06：00—19：00，功率数据采样间隔Δt=1 min，每天采集1 440个点。时间跨度选择为1年，剔除异常数据后，时间跨度确定为360天。读取360天的光伏功率数据，使用储能系统平抑其功率波动。

采用文献[12]中的滑动平均法进行平抑，其中预测方法选择马尔科夫链法[13-14]。滑动平均法可以实现从光伏功率数据中分离出min级波动分量，其关键在于滑动平均时段的选择。经过大量仿真计算，在满足并网波动功率不超过10%装机容量的要求下，滑动平均时段选择10 min较为适宜，即根据光伏功率当前时刻之前的5 min历史数据、当前时刻数据以及未来4 min的预测数据计算当前时刻光伏功率的持续分量与波动分量。将此波动分量作为储能系统的目标功率，如式(1)、(2)所示。

(1)

ΔPt=Ppv,t-Ppv,ref

(2)式中：Ppv,ref是光伏功率持续分量；Ppv,t-i(i=5)为历史功率数据；Ppv,t为当前时刻的光伏功率；Ppv,t+j(j=4)为预测功率数据；ΔPt为储能系统的目标功率。

光伏功率预测曲线和滑动平均目标功率曲线如图1所示。在图1中，光伏功率实际值与滑动平均目标功率之差即为储能系统的目标功率。

图1 光伏功率预测和滑动平均目标功率曲线Fig.1 Curves of PV forecasting power and moving average daily target power

1.2 电池寿命计算

一般将电池循环寿命定义为在容量衰减至某一规定值之前经历的总充、放电次数[15]。循环寿命与充、放电速率、环境温度、最大放电深度等因素有关，许多学者和文献的研究成果表明，电池在运行周期内的放电深度对循环寿命的影响最为显著，最大放电深度越大，电池循环寿命越短[16]。

电池在不同放电深度时对应不同的循环寿命，因此需要将不同放电深度下的循环寿命统一到某一参考值(通常选择放电深度为100%)进行量化比较，即计算其等效循环寿命(equivalent cycle life，ECL)。电池的循环寿命与工作方式密切相关，放电深度(depth of discharge，DoD)越大，循环寿命越短。本文将充放电次数和放电深度作为影响电池循环寿命的主要因素。

通过雨流计数法可以计算电池的放电深度，然后根据电池放电深度与循环寿命的对应关系，计算出电池的等效循环寿命。继而采用等效完全充放电次数来衡量储能系统在1个运行周期(1 天)的损耗情况。等效完全充放电次数计算过程如图2所示。

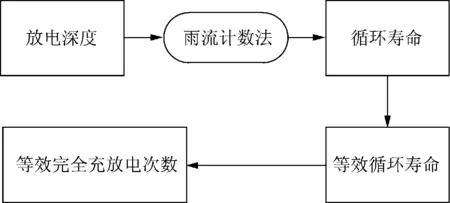
图2 等效完全充放电次数计算流程Fig.2 Calculation flow chart of equivalent charging and discharging times

通常电池生产厂家会通过额定工况下实验将放电深度与电池循环寿命的关系进行标定，本文采用铅酸电池的放电深度与对应的循环寿命。在实际应用中，电池往往不局限于文献[17]所示的放电深度，可根据数据进行拟合得到放电深度与循环寿命的关系曲线，采用式(3)所示的4阶函数表征循环寿命与放电深度的关系，相应曲线如图3所示[18]。

(3)

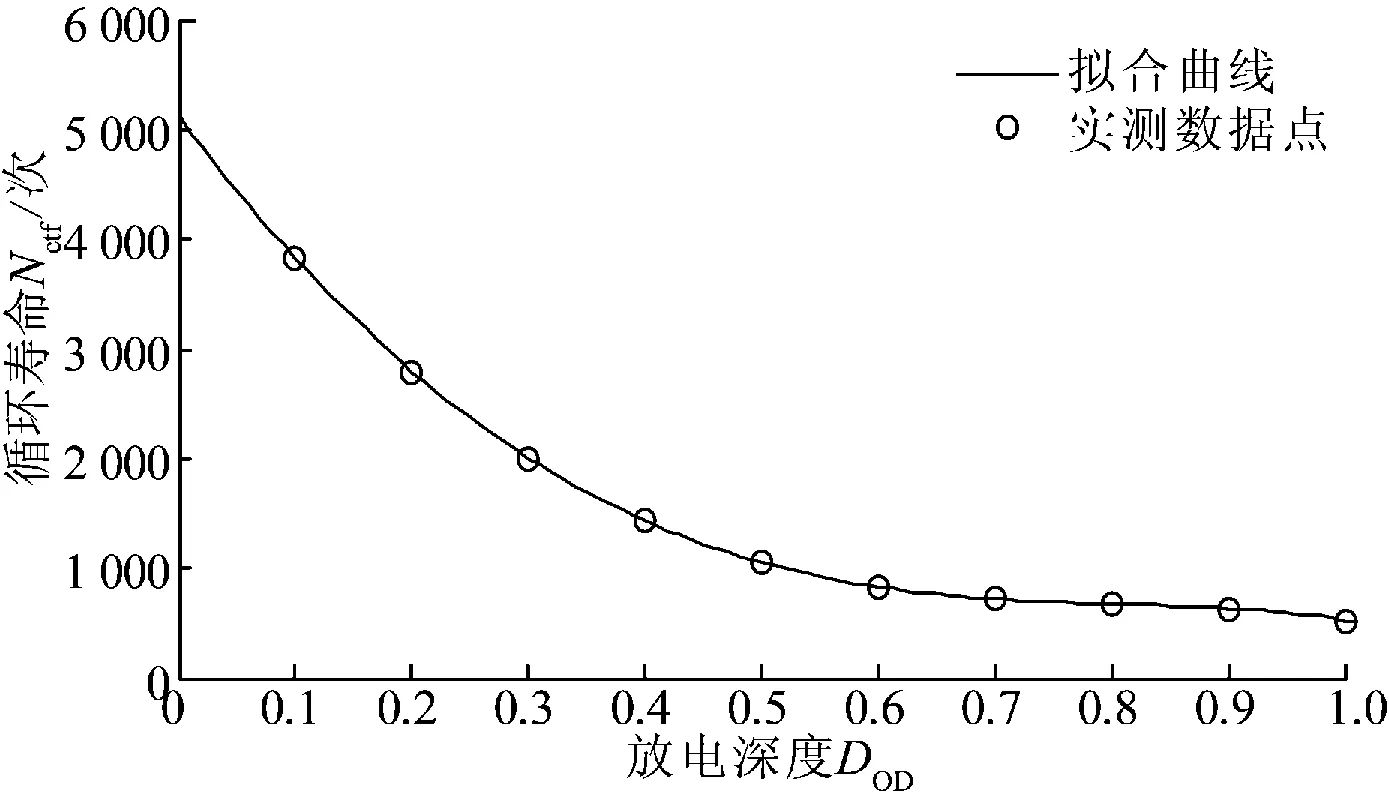
图3 循环寿命与放电深度的关系Fig.3 Relationship of circle life and DoD

将电池的运行周期分解为一系列N个循环周期，放电深度分别为DoD1，DoD2，…，DoDN。设电池第i次循环周期的放电深度为DoDi，则对应的等效循环寿命为

(4)

式中：Nctf(DoD1)为当放电深度为100%时对应的循环寿命；Nctf(DoDi)为当放电深度为DoDi时的循环寿命。

电池在运行周期内等效完全充放电次数为

(5)

通过等效循环寿命L可以计算当前电池的使用寿命，并可用于预测电池寿命。当L=Nctf(DoD1)时，则认为本批次电池组寿命耗尽，需要更换电池组。

2 双向互补电池储能系统控制原理

2组储能电池构成1套储能系统，2个子系统分别记为BESS1与BESS2，共同输出t时刻储能系统的目标功率。光-储联合系统拓扑结构如图4所示。

图4 光-储联合系统拓扑结构Fig.4 Topological structure of PV and ES hybrid system

在电池储能系统动作的任一时刻，确保BESS1与BESS2处于不同的充/放电状态以应对交替出现的光伏功率正/负向波动，并且有：

ΔPt=PBESS1,t+PBESS2,t

(6)

式中PBESS1,t与PBESS2,t分别为BESS1和BESS2在t时刻的输出功率。

运行过程中，若任一组BESSi(i=1,2)达到了充电临界荷电状态SOC，max或放电临界荷电状态SOC,min，则应立即切换2组BESS系统的充/放电状态。电池储能系统充放电状态切换策略如图5所示。

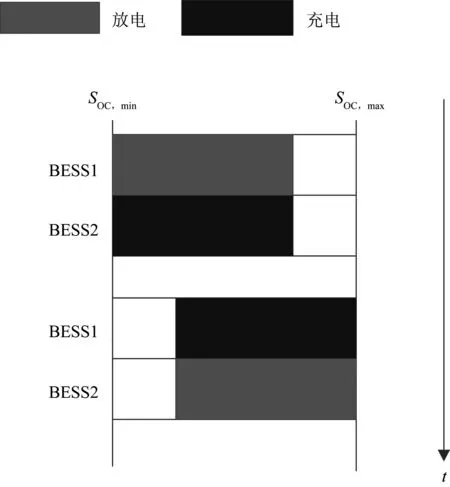
图5 电池储能系统充放电状态切换策略Fig.5 Switching strategy of charging and discharging state of battery energy storage system

记电池储能系统t时刻目标功率为ΔPt，双向互补控制策略描述如下。

当ΔPt<0时，即储能系统通过放电来填补负向光伏功率的波动，则其放电功率为

(7)

式中：Ped,max为储能系统最大放电功率约束；Ped,soc为储能系统最小荷电状态约束，其：

(8)

式中：Soc,t-1为t-1时刻的储能系统荷电状态；Soc,min为设定的储能系统临界放电状态，即荷电状态下限值；ηd为储能系统放电效率；Cap为储能系统总容量；Δt为仿真时间间隔。

当ΔPt>0时，即储能系统通过充电来抵消正向光伏功率的波动。则其充电功率为

(9)

式中：Pec,max为储能系统最大充电功率约束；Pec,soc为储能系统最大荷电状态约束，其计算公式如下：

(10)

式中：Soc,max为设定的储能系统临界充电状态，即荷电状态上限值；ηc为储能系统放电效率。

3 算例及经济性分析

3.1 算例分析

利用Matlab2012仿真软件，对本文提出的双向互补电池储能系统控制策略进行仿真分析。所选择的双向互补电池储能系统容量参数如下：BESS1的容量为4.5 MW·h, BESS2的容量为4.5 MW·h；单电池储能系统的容量为4.5 MW·h。该储能系统在单BESS控制策略下的目标功率曲线如图6所示，目标功率就是单储能系统的吞吐功率。

图6 单BESS控制策略下的储能充放电功率Fig.6 Charging and discharging power of energy storage under single BESS control strategy

从图6中可以看出，当任一组BESSi(i=1,2)达到充/放电临界荷电状态时，则立即切换2组BESS的充/放电状态，因此充电和放电临界荷电状态限定值的设定对控制效果和最终的电池储能系统整体损耗都有影响。为了考察不同充电或放电临界荷电状态限定值下的控制效果，设定7组充电和放电临界荷电状态限定值，并以其中2组为例进行分析和说明，其输出功率曲线如图7所示。

图7 储能系统输出功率Fig.7 Charging and discharging output power of energy storage system

图8为2种控制策略下的储能系统荷电状态变化情况，由图8可知，2组充放电临界荷电状态限定值下的控制效果不同，表现在功率曲线和荷电状态曲线的形态不同。充放电临界荷电状态限定范围越窄，双向互补的2组电池储能系统的充放状态转换就越频繁。

3.2 经济性分析

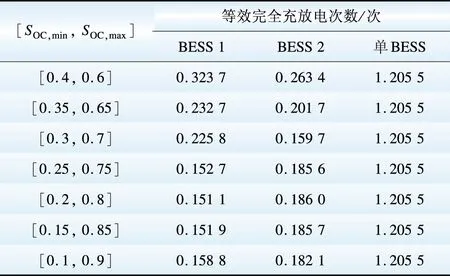
为考察充放电临界荷电状态限定值对储能系统损耗的影响，计算不同充放电临界荷电状态限定范围下双向互补电池储能系统控制策略与传统单BESS控制策略下的等效完全充放电次数，结果如表1所示。

以BESS1与BESS2的等效完全充放电次数之和为纵坐标，以充放电临界荷电状态限定值上下限值之差为横坐标作图，不同荷电状态区间双BESS的等效完全充放电次数之和如图9所示。

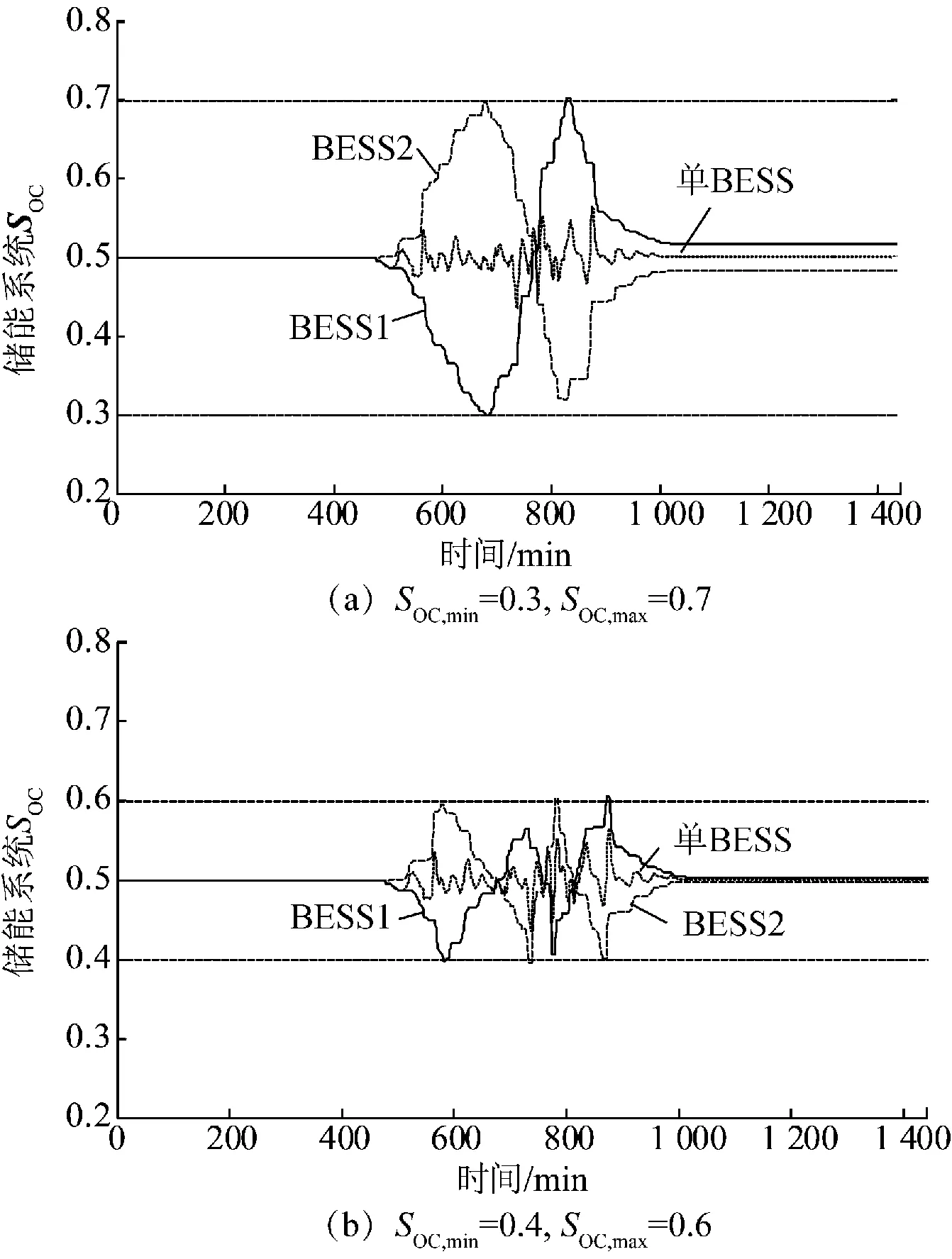
图8 2种控制策略下的储能系统SOCFig.8 SOC of energy storage system under two control strategies

由于BESS1与BESS2的容量之和是单BESS的2倍，则认为双向互补电池储能系统控制策略的初始成本是单BESS控制方式初始成本的2倍。如果双向互补控制策略下的损耗小于单BESS控制方式的一半，则双向互补控制策略具有经济优势，因为其使用寿命大于单BESS控制方式的2倍。由图9可知，BESS1与BESS2等效完全充放电次数之和小于单BESS等效完全充放电次数的一半，即双向互补电池储能系统控制策略更具有经济性。

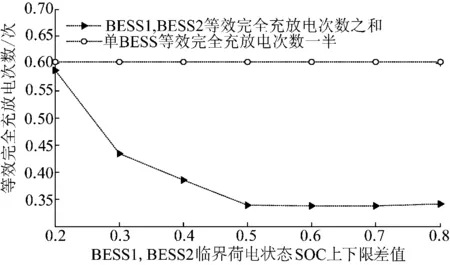
图9 不同SOC区间双BESS的等效完全充放电次数之和Fig.9 Equivalent charging and discharging times of double BESS under different SOC intervals

当荷电状态区间上下限值为0.6时，即SOC,min=0.2,SOC,max=0.8，BESS1与BESS2的等效完全充放电次数之和取最小值0.337 1,因此确立充放电临界荷电状态限定值[0,2,0.8]为控制策略的最佳区间，在此条件下的储能系统输出功率和SOC变化情况如图10所示。

图10 SOC区间为[0.2,0.8]时储能系统输出功率和SOCFig.10 Output power and SOC of energy storage system when SOC interval is [0.2,0.8]

由图10可知，当充放电临界荷电状态限定值为[0,2,0.8]时，由于BESS1与BESS2的等效完全充放电次数之和取最小值，即此控制策略下的电池寿命损耗最小，所以2组电池储能系统的充放状态转换频繁程度低于图8中2种充放电临界荷电状态限定范围情况下的充放状态转换频繁程度。

4 结论

本文基于双向互补电池储能系统控制策略完成对储能系统目标功率的吞吐。通过考察不同充放电临界荷电状态限定值下的控制效果，确立充放电临界荷电状态最佳限定区间为[0.2, 0.8]。对双向互补电池储能系统控制策略与传统控制策略下的储能系统损耗进行比较，仿真结果表明，双向互补电池储能系统控制策略更具有经济性。

[1]刘伟，彭冬，卜广全，等．光伏发电接入智能配电网后的系统问题综述[J]．电网技术，2009，33(19)：1-6． LIU Wei, PENG Dong, BU Guangquan, et al. Asurvey on system problems in smart distribution network with grid-connected photovoltaic generation[J].Power System Technology,2009, 33(19):1-6.

[2]丁明，王伟胜，王秀丽，等．大规模光伏发电对电力系统影响综述[J]．中国电机工程学报，2014，34(1)：1-14． DING Ming, WANG Weisheng, WANG Xiuli, et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE, 2014，34(1)：1-14.

[3]BILLINTON R B．Impacts of energy storage on power system reliability performance[C]//Canadian Conference on Electrical and Computer Engineering. Saskatchewan，Canada: IEEE，2005：494-497.

[4]丁明，徐宁舟，毕锐．用于平抑可再生能源功率波动的储能电站建模及评价[J]．电力系统自动化，2011，35(2)：66-72． DING Ming, XU Ningzhou, BI Rui. Modeling of BESS for smoothing renewable energy output fluctuations[J].Automation of Electric Power Systems,2011,35(2):66-72.

[5]汪海蛟，江全元．应用于平抑风电功率波动的储能系统控制与配置综述[J]．电力系统自动化，2014，38(19)：126-135． WANG Haijiao， JIANG Quanyuan. An overview of control and configuration of energy storage system used for wind power fluctuation mitigation[J].Automation of Electric Power Systems,2014,38(19):126-135.

[6]高明杰，惠东，高宗和，等．国家风光储输示范工程介绍及其典型运行模式分析[J]．电力系统自动化，2013，37(1)：59-64． GAO Mingjie, HUI Dong, GAO Zonghe, et l. Presentation of national wind/photovoltaic/energy storage and transmission demonstration project and analysis of typical operation modes[J].Automation of Electric Power Systems,2013,37(1):59-64.

[7]杨水丽，惠东，李建林，等．适用于风电场的最佳电池容量选取的方法[J]．电力建设，2010，31(09)：1-4． YANG Shuili, HUI Dong, LI Jianlin, et al. Selection of theoptimal battery capacity for wind farm[J]. Electric Power Construction,2010,31(9):1-4.

[8]JIANG Q，WANG H．Two-time-scale coordination control for a battery energy storage system to mitigate wind power fluctuations[J]．IEEE Transactions on Energy Conversion，2013，28(1)：52-61.

[9]LI X．Fuzzy adaptive Kalman filter for wind power output smoothing with battery energy storage system[J]．IET Renewable Power Generation，2012，6(5)：340-347.

[10]洪海生，江全元，严玉婷．实时平抑风电场功率波动的电池储能系统优化控制方法[J]．电力系统自动化，2013，37(1)：103-109． HONG Haisheng, JIANG Quanyuan, YAN Yuting. An optimization control method of battery energy storage system with wind power fluctuations smoothed in real time[J].Automation of Electric Power Systems,2013,37(1):103-109.

[11]王刚，邱晓燕，张晓晨，等．平滑风电功率的电池储能系统优化控制策略[J]．电力系统及其自动化学报，2015，27(8)：66-70． WANG Gang, QIU Xiaoyan, ZHANG Xiaochen, et al.Optimized control strategy for battery energy storage system to smooth wind power output[J]. Proceedings of the CSU-EPSA, 2015, 27(8):66-70.

[12]林卫星，文劲宇，艾小猛，等．风电功率波动特性的概率分布研究[J]．中国电机工程学报，2012，32(1)：38-46． LIN Weixing, WEN Jinyu, AI Xiaomeng, et al. Probability density function of wind power variations[J]. Proceedings of the CSEE, 2012, 32(1):38-46.

[13]周封，金丽斯，刘健，等．基于多状态空间混合Markov链的风电功率概率预测[J]．电力系统自动化，2012，36(6)：9-33． ZHOU Feng, JIN Lisi, LIU Jian, et al. Probabilistic wind power forecasting based on multi-state space and hybrid Markov chain models[J]. Automation of Electric Power Systems,2012,36(6):29-33.

[14]周封，金丽斯，王丙全，等．基于高阶Markov链模型的风电功率预测性能分析[J]．电力系统保护与控制，2012，40(6)：6-10． ZHOU Feng, JIN Lisi, WANG Bingquan, et al. Analysis of the wind power forecasting performance based on high-order Markov chain models[J]. Power System Protection and Control, 2012，40(6)：6-10.

[15]SAUER D U，WENZL H．Comparison of different approaches for life-time prediction of electrochemical systems-using lead acid batteries as example[J]．Journal of Power Sources，2008，176(2)：477-483.

[16]WAN Y．Summary report of wind farm data[R]．Golden：National Renewable Energy Laboratory，2008.

[17]BINDNER H，CRONIN T，LUNDSAGER P，et al．Lifetime modeling of lead acid batteries[R]．Roskilde：Risø National Laboratory，2005.

[18]程成．用于可再生能源发电并网技术的混合储能控制策略研究[D]．北京：华北电力大学，2014． CHENG Cheng.Research of hybrid energy storage control strategy for renewable energy power generation and grid connected technology[D]. Beijing: North China Electric Power University, 2014.

(编辑张小飞)

Control Strategy and Economic Analysis of Energy Storage System Based on Bidirectional Complementary

ZHANG Hua1, ZHANG Bin2, JI Tianming3, HAN Xiaojuan1

(1.School of Control and Computer Engineering, North China Electric Power University, Beijing 102206，China; 2. Sanhe Electric Power Company, State Grid Jibei Electric Power Company, Sanhe 065200, Hebei Province, China；3. Information System International Company, NARI Group Corporation, Nanjing 211106, China)

The high cost and immature control technology of energy storage system restrict the large-scale application of battery energy storage system. With full consideration of the economy of battery energy storage system, this paper proposes the control strategy for energy storage system based on bidirectional complementary, in which the bidirectional complementary battery energy storage system is composed of two groups of batteries. We calculate the the depth of discharge (DoD) by rain flow count method, in order to characterize the cycle life of the battery; and establish the charge and discharge control model for bidirectional complementaryenergy storage system. Taking the measured data of an photovoltaic-energy storage hybrid power station as example, we simulate and analyze the economy of the control strategy for bidirectional complementary battery energy storage system, in the different limited range of the critical state of charge during charge-discharge in energy storage system. The simulation results show that, compared with the control strategy of single energy storage system, the the control strategy of battery energy storage system based on bidirectional complementary can effectively improve the service life of the system and reduce the cost of energy storage system, which has a good prospect of engineering application.

energy storage system; bidirectional complementary; control strategy; economic analysis

国家自然科学基金项目(51577065)；国家电网公司科技项目(KY-SG-2016-204-JLDKY)

TM 912

1000-7229(2016)08-0096-06

10.3969/j.issn.1000-7229.2016.08.015

2016-03-11

张婳(1992)，女，硕士，主要从事电池储能控制、经济性评估等方面的研究工作；

张斌(1989)，男，硕士，主要研究方向为新能源发电控制技术和储能技术；

籍天明(1991)，男，硕士，主要从事新能源发电控制技术、数据挖掘等方面的研究工作；

韩晓娟(1970)，女，博士，教授，主要从事新能源发电控制技术、故障诊断、信息融合和检测技术等方面的研究工作。

Project supported by National Natural Science Foundation of China (51577065)