高等级海况条件下移动式海上基地动力响应分析

李青美, 吴林键, 王元战, 肖 忠, 李 怡



高等级海况条件下移动式海上基地动力响应分析

李青美1, 吴林键1, 王元战1, 肖 忠1, 李 怡2

(1. 天津大学水利工程仿真与安全国家重点实验室, 高新船舶与深海开发装备协同创新中心, 天津 300072; 2. 重庆交通大学河海学院, 重庆 400074)

针对半潜式超大型浮式结构中典型的移动式海上基地(Mobile Offshore Base, MOB)在高等级海况下的动力响应问题展开研究。在MOB结构“刚性模块-柔性连接构件(Rigid Modules and Flexible Connectors, RMFC)”模型的前提下, 根据动力学基本原理, 经理论推导并计算得到MOB分别在6、7、8级海况的随机波激励下, 其上各模块的动力响应位移结果。详细分析了MOB结构同一模块在不同海况条件下的动力响应位移随浪向角及连接构件刚度的变化规律。研究成果可为半潜式超大型浮式结构动力响应研究及结构优化设计提供一定的技术支撑。

高等级海况; 移动式海上基地; 动力响应

移动式海上基地(Mobile Offshore Base, MOB)[1]是半潜式超大型浮式结构中的典型代表, 其几何尺度可按公里计。MOB是一种通过特殊设计的连接构件将多个具备自航模式的模块相连接, 并由锚泊定位系统固定的多用途海上浮式基地, 其不仅可作为军用飞机的临时避风港湾, 也可作为战备物资及货物的储存中转站[2]。图1为MOB结构的概念设计图, 图示中单个模块是由1个上体、8个立柱及2个浮箱构成。由于MOB结构的水动力性能较好, 更加能够适应深远海域中复杂且恶劣的海洋环境, 因此, 大量的国内外学者对其开展了一系列的研究工作。其中, MOB在深远海域受不同环境荷载激励下的动力响应问题更是成为了许多学者研究的重点。

当前, 对于超大型浮式结构(Very Large Floating Structure, VLFS)的动力响应计算理论可大致归为3类: 势流理论(适用于刚性模块)、水弹性理论(适用于柔性模块)及其他方法(浮体及多浮体系统运动理论、有限元方法等)。当考虑VLFS模块为刚性时,可基于势流理论分析VLFS的动力响应。Riggs等[3]基于三维势流理论, 运用HYD-R-AN程序作为波浪激励响应, 在频域内计算得到MOB各模块的动力响应位移。张波[4]基于势流理论对MOB进行三维水动力分析, 利用商业软件Sesam分别计算得到3、5、7个模块的MOB模型在8个浪向角和46个波浪频率下的水动力系数和波浪载荷, 并在频域内计算了MOB各模块在规则波和不规则波浪作用下的运动响应。汪伍洋[5]针对多体超大型浮式结构物, 利用势流理论对其水动力进行了分析计算。运用HydroD计算得到了MOB在随机波作用下的波浪力和水动力系数, 并在频域内求解得到了各模块在不同浪向角下的运动位移。谢楠等[6]基于三维线性势流理论, 分析了两个距离较近浮式结构相互作用的水动力响应, 最终的数值计算结果能够较好地与试验结论相吻合。

当考虑VLFS模块为柔性时, 其模块在海洋环境荷载的作用下发生刚体运动的同时, 其自身也将发生柔性变形。由于VLFS几何尺度巨大, 其自身的柔性变形必将会对周围流场产生影响, 当流场发生变化时, 作用于VLFS上的激励力也将随之发生变化, 因此在对VLFS动力响应分析中应考虑结构的水弹性效应[7]。Che等[8], Ertekin等[9], 以及Riggs等[10]是最早将二维水弹性切片理论用于VLFS动力响应分析当中, 将VLFS中各模块视为弹性梁, 计算VLFS的运动位移及变形。Alex等[11]分别研究了VLFS在浅水、有限水深和深水中的水弹性响应, 并提出了浅水中VLFS水弹性响应的近似简化算法, 从结果上看, 能与文献中的数据相对应。吴有生[12]首次将三维势流理论运用到三维水弹性问题分析当中, 其研究表明: 特别是针对任意几何形状的VLFS, 三维水弹性理论的计算精度要比二维水弹性切片理论更高。付世晓等[13]将三维水弹性理论与有限元法相结合, 以铰接型式连接构件的VLFS为例, 计算得到了较为理想的结果。我国上海交通大学王志军、李润培、舒志、刘应中等[14-18]对箱式VLFS的水弹性理论及其动力响应分析进行了大量的研究工作, 包括理论分析、模型试验、数值计算等, 并取得了大量的研究成果。

同时, VLFS的结构形式普遍为多浮体系统, 因此, 也可采用浮体及多浮体系统运动理论来求解VLFS结构的动力响应。刘超[19]基于多浮体运动理论,得出了浮体的频域运动方程, 以3个不同的计算模型为例, 通过Sesam/Wadam软件计算结构的水动力, 分析了其上连接构件的刚度、不同海况及浪向角、模块数量对VLFS运动响应的影响。Chakrabarti[20]将直接矩阵法和多重散射法构成的混合分析方法拓展到对浮体及多浮体系统在波浪中的动力响应分析中, 并充分考虑了多浮体系统对波浪的辐射和绕射效应, 并将计算结果与试验数据进行了相互印证。沈庆等[21]采用多刚体力学的Huston方法对铰接连接的多浮体系统进行动力响应分析。陈徐均等[22]针对多浮体系统, 采用频域、时域的综合法, 探讨其在波浪激励下的动力响应, 其计算结果能够与试验实测数据相吻合。

上述文献中所提及的理论研究方法, 其计算结果的精度较高且具有较强的普遍适用性, 但其中也存在较大的弊端: 即不论是势流理论、水弹性理论或其他分析方法, 其基本理论原理相对较为复杂, 且求解过程中耗时较长, 在VLFS初始设计阶段的方案比选过程中, 没必要要求其计算结果的精度达到施工图设计时的误差范围。故本文针对MOB结构的典型概念设计, 在“刚性模块-柔性连接构件(Rigid Modules and Flexible Connectors, RMFC)”计算模型为假设前提的基础上, 研究其各模块在高等级海况条件下的动力响应。应值得注意的是, MOB结构在深远海域内必将受到多因素环境荷载的激励, 例如: 风荷载、海流力以及波浪力等, 而本文暂且仅考虑随机不规则波浪荷载对结构的激励, 其余荷载因素暂时忽略。同时, 文中结合MOB结构自身的特点, 避开了相对复杂的线性势流理论, 考虑当MOB结构相邻两模块之间连接构件的刚度发生变化时, 分析MOB各模块在高等级海况(6、7、8级)条件下的动力响应, 并探讨MOB结构同一模块在不同海况条件下的动力响应位移变化规律。最终, 大量计算结果的统计和分析可为MOB结构动力响应研究及结构的优化设计提供一定的参考。

1 MOB动力响应分析研究思路

根据浮式结构动力学的相关理论, 将MOB的多模块结构看作多自由度体系, 可将结构整体按如图2所示概化。

图示中M1、M2、M3分别表示MOB结构中的第1、2、3个模块, C1、C2、C3、C4分别表示其上各连接构件。根据结构动力学D’Alembert原理, MOB结构多自由度体系的整体动力学平衡方程可写为:

式中:为结构的广义质量矩阵,=s+f,s为结构质量矩阵,f为结构附加质量矩阵;为结构运动位移的二阶导数;f为阻尼系数矩阵,为结构运动位移的一阶导数;为刚度矩阵,=s+f, 其中,s为整体刚度矩阵,f为静恢复力系数矩阵;表示结构运动的位移,为海洋环境激励力矩阵, 本文中即为随机不规则波浪荷载。同时, 由于不规则波浪荷载应是随时间在发生变化, 故公式(1)中的各系数矩阵也应为时变项, 则公式(1)可写为:

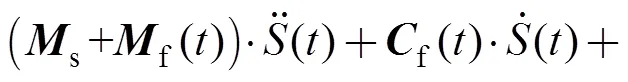
(2)

由于MOB尺度巨大, 对其结构进行整体研究相对较复杂, 故采取隔离法来对其各单模块进行分析, 则MOB结构单模块的动力学方程为:

在公式(3)中, 由于针对MOB单模块进行隔离分析, 故整体刚度矩阵s已不复存在; 同时, 柔性连接构件的约束荷载c()由内力变为了外力, 故将其写在等式右端, 该项也为时变项。综上所述, 在任意时刻, MOB单模块在随机波浪力激励下将对应纵荡、横荡、垂荡、横摇、纵摇、艏摇这6个自由度方向的运动, 因此, 可根据公式(3)建立MOB单模块在6个运动自由度方向上的动力学方程组, 联立求解得到MOB结构各模块在不同高等级海况、不同浪向角、不同连接构件刚度下的动力响应位移和转角, 并分析其结果随以上各因素的变化规律。公式(3)中各水动力系数的简易计算公式可根据结构动力学理论推导得出, MOB结构的波浪力可基于浮体Morison公式来计算得到。MOB的整体坐标系、局部坐标系′′′及波浪坐标系可如图2所示, 波浪浪向角为, 其值在0°~90°范围变化。MOB动力响应分析的具体过程及理论算法的正确性、有效性及可行性验证请详见文献[23]中笔者的研究成果。

2 高等级海况及其波浪统计参数

根据在海面开阔视野范围内的海面状况、波浪的变化形状及其破裂程度等因素, 可将海况等级分为10级, 当海况等级在5级以上(含5级)时为高等级海况(High Sea State)[24]。根据现有文献资料[25~27], 得到了位于北太平洋开敞海面各不同等级海况下的波浪统计参数, 如表1所示。本文以典型MOB概念设计作为工程实例, 分别研究该结构各模块在6、7、8级海况条件下(后简称SS6、SS7、SS8)的动力响应变化情况。

表1 北太平洋开场海面各级海况条件参数统计

3 工程实例

3.1 MOB原型概念设计

MOB原型概念设计的几何尺度可参考Yu[25]、丁伟[26]、吕海宁[27]等的科研成果, 工程实例的具体尺寸参数如图3所示。MOB相邻两模块之间共存在2个连接构件, 并将其连接构件概化为三个方向上的弹簧模型, 具体过程可详见笔者的前期研究成果[23]。

3.2 计算条件

由于MOB结构连接构件的刚度是影响其动力响应及其自身约束荷载的关键因素[28], 因此, 在本文的计算探讨过程中, 也将连接构件的刚度作为一个重要的变量。根据文献资料[25-27], 选取6个连接构件的刚度大小作为计算依据。同时, 在不同海况条件下, 浪向角的不同也将会对计算结果产生影响。综上所述, 本文以3个海况等级、6个浪向角、6种连接构件刚度共108种组合作为计算条件, 并且令连接构件的刚度在纵、横、垂向(方向)的大小保持一致, 如表2所示。

注:1~6代表连接构件刚度, 分别为106~1011N/m;K、K、K表示构件在、、方向的刚度

4 高等级海况下MOB动力响应结果分析

根据表2中的计算条件, 结合MOB结构时域动力响应理论研究成果及数值计算程序[23], 可计算得到工程实例MOB中3个模块在不同海况等级、不同浪向角、不同连接构件刚度条件下, 其6个自由度方向上的动力响应位移, 取计算时长=3 600 s, 并统计得到不同情况下的最大值(最不利结果)进行分析。由于本文篇幅有限, 故仅以M1的结果为代表进行论述, M2、M3的计算结果详见文献[23], 如图4~图6所示, 为不同海况条件下, M1的动力响应结果随浪向角的变化图示。

4.1 六、七、八级海况下M1的计算结果

从图4~图6中可以看出: (1)M1在SS6~SS8条件下, 其6个自由度方向上的最大动力响应位移及转角随浪向角的变化趋势能够保持一致。M1在纵荡和纵摇方向上的最大位移及转角随浪向角的增加呈现出递减的变化, 而横荡、垂荡的变化趋势与前两者恰好相反; 同时, 在横摇、艏摇方向的转角随浪向角的变化则呈现出先增后减的变化规律; (2)从数值上看, 纵荡、纵摇方向上的最大值出现在浪向角=0°时, 而横荡、垂荡方向上的最大值则出现在=90°时, 横摇、艏摇的最大值则出现在当=75°~85°之间; (3)从图中横摇、纵摇及艏摇的变化图示中可以看出来, 当连接构件的刚度为6时, MOB单模块在3个转动自由度方向上的转角与其余刚度时的计算结果存在差异, 但其差别均在0.001~0.01 rad(0.057 3°~0.573°)范围内, 相比于MOB结构以公里计的几何尺寸而言, 这种差别可忽略不计; (4)从图示中横荡、垂荡两个方向上的位移计算结果上看, 当浪向角=90°时, 其动力响应位移的大小与连接构件的刚度无关。其主要原因在于: 当=90°时, 在方向上MOB各个模块所受波浪激励力均一样, 在求解方向动力学平衡方程组时, 相邻两个模块的达朗贝尔动力学平衡方程中各个系数完全一致, 因此, 求解所得到的运动位移与连接构件的刚度无关, 详细理论推导及数值计算过程详见文献[23]。

4.2 不同海况条件下MOB同一模块动力响应对比

为了比较在不同海况条件下, MOB模块的动力响应位移、转角随连接构件刚度和浪向角的变化情况, 建立三维坐标系, 以横坐标为刚度, 纵坐标为浪向角, 竖坐标为动力响应位移(或转角), 绘制得到了工程实例中MOB各模块在SS6、SS7、SS8条件下, 6个自由度方向上的最大动力响应位移、转角对比。同理, 以M1为代表, M2、M3的计算结果详见文献[23], 如图7所示。

从图7可以看出: (1)不同海况条件下, M1在6个自由度方向上的最大动力响应位移(或转角)随浪向角的变化趋势能够保持一致, 其数值上均呈现出SS8>SS7>SS6的特征规律, 即海况等级越高, MOB各单模块的运动幅度就越大, 这与实际情况能够相吻合; (2)但相对而言, 在SS6和SS7条件下, M1在6个自由度方向上的运动位移及转角在数值上较为接近, 尤其是当连接构件刚度较大时, M1在纵荡方向上运动位移的变化符合上述规律。同时, 在横荡、垂荡方向上位移的变化情况亦是如此, 以及当浪向角较大时, 横摇及纵摇方向的转角计算结果在SS6及SS7条件下非常一致; (3)在SS8条件下M1的动力响应位移及转角比在SS6和SS7条件下计算得到的结果更大, 尤其是在横荡和垂荡两个方向上, 运动位移相对较大。此时, 建议应该采取相应的一些相应的措施, 以减少结构物在高等级海况条件下的运动位移。

5 结论

本文研究了MOB结构在高等级海况条件下的动力响应。在MOB结构“RMFC”计算模型的前提下, 基于D’Alembert动力学原理分别计算得到MOB结构在6、7、8级海况随机波激励下, 其各模块的动力响应结果。其中, 理论分析过程及数值计算方法的正确性、可行性及有效性均可得以验证。同时, 详细分析了MOB结构同一模块在不同海况条件下的动力响应位移随浪向角及连接构件刚度的变化规律, 研究成果可为半潜式超大型浮式结构动力响应研究及结构优化设计提供一定的技术支撑。

[1] 崔维成, 吴有生, 李润培. 超大型海洋浮式结构物动力特性研究综述[J]. 船舶力学, 2001, 5(1): 73-81. Cui Weicheng, Wu Yousheng, Li Runpei. Recent researches on dynamic performances of very large floating structures[J]. Journal of Ship Mechanics, 2001, 5(1): 73-81.

[2] Mcallister K R. Mobile offshore bases an overview of recent research[J]. Marine Science and Technology, 1997, 3(2): 173-181.

[3] Riggs H R, Ertekin R C, Mills T R J. Impact of connector stiffness on the response of a multi-module mobile offshore base[C]// International Society of Offshore and Polar Engineers. Proceeding of the Eighth International Offshore and Polar Engineering Conference. Montreal: ISOPE press, 1998: 200-207.

[4] 张波. 超大型浮式结构物动力响应与风险评估研究[D]. 镇江: 江苏科技大学, 2013. Zhang Bo. Hydrodynamic response and risk assessment of very large floating structure[D]. Zhenjiang: Jiangsu University of Science and Technology, 2013.

[5] 汪伍洋. 多体超大型浮式结构物连接器的设计及载荷的初步分析[D]. 镇江: 江苏科技大学, 2014. Wang Wuyang. Design of connectors and analysis of its load in multi-very large floating structure[D]. Zhenjiang: Jiangsu University of Science and Technology, 2014.

[6] 谢楠, 郜焕秋. 波浪中两个浮体水动力相互作用的数值计算[J]. 船舶力学, 1999, 3(2): 7-15. Xie Nan, Gao Huanqiu. Numerical calculation of hydrodynamic interaction of two bodies floating in waves[J]. Journal of Ship Mechanics, 1999, 3(2): 7- 15.

[7] 崔维成, 吴有生, 李润培. 超大型海洋浮式结构物开发过程中需要解决的关键技术问题[J]. 海洋工程, 2000, 18(3): 1-8. Cui Weicheng, Wu Yousheng, Li Runpei. Technical problems in the development of very large floating structures[J]. Ocean Engineering, 2000, 18(3): 1-8.

[8] Che Xiling, Wang Dayun, Wang Minglun, et al, Two dimensional hydro elastic analysis of very large floating structures[J]. Marine Technology, 1992, 29(1): 13-24.

[9] Ertekin R C, Riggs H R, Seidl L H, et al. The design and analysis of very large floating structures[J]. Ocean Engineering, 1990, 35(2): 58-63.

[10] Riggs H R, Che X L, Ertekin R C. Hydroelastic response of very large floating structures[J]. International Journal of Offshore & Polar Engineering, 1991, 1(4): 307-316.

[11] Andrianov A I, Hermans A J. The influence of water depth on the hydro-elastic response of a very large floating platform[J]. Marine Structures, 2003, 16(5): 355-371.

[12] Wu Yousheng. Hydro elasticity of Floating Bodies[D]. UK: Brunel University , 1984.

[13] Fu Shixiao, Torgeir M, Chen Xujun, et al. Hydro elastic analysis of flexible floating interconnected structures[J]. Ocean Engineering, 2007, 34(11): 1516-1531.

[14] 王志军, 李润培, 舒志. 箱式超大型浮体结构在规则波中的水弹性响应研究[J]. 海洋工程, 2001, 19(3): 9-13. Wang Zhijun, Li Runpei, Shu Zhi. Study on hydroelastic response of box-shaped very large floating structure in regular waves[J]. Ocean Engineering. 2001, 19(3): 9-13.

[15] 王志军, 李润培, 舒志. 箱式超大型浮体结构在不规则波中的水弹性响应[J]. 上海交通大学学报, 2001, 35(10): 1477-1480. Wang Zhijun, Li Runpei, Shu Zhi. Hydroelastic response of box-typed very large floating structure in irregular waves[J]. Journal of Shanghai Jiaotong University, 2001, 35(10): 1477-1480.

[16] 舒志, 李润培, 王志军. 箱式超大型浮式结构物在波浪中的运动响应研究[J]. 中国海洋平台, 2002, 17(3): 1-5. Shu Zhi, Li Runpei, Wang Zhijun. A study on the motion of very large floating structure in waves[J]. China Offshore Platform, 2002, 17(3): 1-5.

[17] 王志军, 李润培, 舒志. 结构刚度变化对箱式超大型浮体结构水弹性响应的影响[J]. 船舶力学, 2003, 7(1): 56-62. Wang Zhijun, Li Runpei, Shu Zhi. Effect of structural stiffness on hydroelastic response of box- typed very large floating structure[J]. Journal of Ship Mechanics, 2003, 7(1): 56-62.

[18] Liu Yingzhong, Cui Weicheng. Mat-Type VLFS on a seaway over an Uneven Bottom[J]. Ship Mechanics, 2007, 11(3): 321-327.

[19] 刘超. 超大型浮体多模块柔性连接结构响应研究[D]. 北京: 中国舰船研究院, 2014. Liu Chao. Research on structural response of multi- module flexible connectors for very large floating structures[D]. Beijing: Academy of Ship in China, 2014.

[20] Chakarbarti S K. Response due to moored multiple structure interaction[J]. Marine Structure, 2001, 24: 231-258.

[21] 沈庆, 陈徐均. 系泊多附体系统流固耦合和浮体间耦合动力分析[J]. 中国造船, 2002, 43(2): 81-84. Shen Qing, Chen Xujun. Dynamic analysis of a mooring multi-body system coupled with fluid and among bodies[J]. Shipbuilding of China, 2002, 43(2): 81-84.

[22] 陈徐均, 沈庆, 孙芦忠, 等. 柔性连接多浮体在不规则波中运动的预报方法[J]. 水动力学研究与进展: A辑, 2000, 15(4): 444-448. Chen Xujun, Shen Qing, Sun Luzhong, et al. A prediction method of motions of a moored flexibly joint multibody floating system responding to irregular waves[J]. Journal of Hydrodynamics(A), 2000, 15(4): 444-448.

[23] 吴林键. 深水超大型浮式结构连接构件动力特性研究[D]. 重庆: 重庆交通大学, 2015. Wu Linjian. Study on dynamic characteristics of connectors in very large floating structure in deep water[D]. Chongqing: Chongqing Jiaotong University, 2015.

[24] Huang Shusheng. Analysis of the sea condition characteristics in Nan-ji Sea Area[J]. Marine Science Bulletin, 1998, 17(3): 90-96.

[25] Yu Lan. Study on dynamic responses of mobile offshore base connectors[J]. China Ocean Engineering, 2003, 17(4): 469-479.

[26] 丁伟. 移动式海上基地试验研究[D]. 上海: 上海交通大学, 2004. Ding Wei. Experimental research on mobile offshore base[D]. Shanghai: Shanghai Jiaotong University, 2004.

[27] 吕海宁. 超大型浮体水动力试验研究[D]. 上海: 上海交通大学, 2004. Lü Haining. Hydrodynamics experiment research on very large floating structure[D]. Shanghai: Shanghai Jiaotong University, 2004.

[28] Gene R, Robert Z, Paul P, et al. Mobile offshore base[C]// International Society of Offshore and Polar Engineers. Proceeding of the Eighth International Offshore and Polar Engineering Conference. Montreal: ISOPE Press, 1998: 524-529.

Hydrodynamic response of a mobile offshore base under high sea states

LI Qing-mei1, WU Lin-jian1, WANG Yuan-zhan1, XIAO Zhong1, LI Yi2

(1. State Key laboratory of Hydraulic Engineering Simulation and Safety, Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Tianjin University, Tianjin 300072, China; 2. School of River and Ocean Engineering, Chongqing Jiaotong University, Chongqing 400074, China)

This study investigates the hydrodynamic response of a mobile offshore base (MOB) with rigid modules and flexible connectors under high sea states, where the MOB is a typical, semi-submersible, and very large floating structure. The dynamic response results of each module under the random waves of sea states 6 (SS6), 7 (SS7), and 8 (SS8) were solved based on the theory of structural dynamics and using theoretical derivation. The change rules of the hydrodynamic response displacement of the same module under different high sea states were specifically analyzed, and various wave angles and the connector stiffness were considered. These results provide significant technical support for hydrodynamic response determination and the optimal design of semi-submersible and very large floating structures.

high sea state; mobile offshore base; hydrodynamic response

(本文编辑: 李晓燕)

[National Natural Science Foundation of China, No.51279128, No. 51479133; National Natural Science Fund for Innovative Research Groups Science Foundation, No.51321065; Construction Science and Technology Project of Ministry of Transport of the People’s Republic of China, No.2014328224040]

Oct. 13, 2015

P751

A

1000-3096(2016)08-0129-09

10.11759/hykx20151113001

2015-11-13;

2016-01-22

国家自然科学基金(51279128, 51479133); 国家自然科学基金创新研究群体科学基金(51321065); 交通运输部交通建设科技项目(2014328224040)

李青美(1978-), 女, 山东青岛人, 博士研究生, 主要研究方向为港口、海岸及近海工程, 电话: 15522102977, E-mail: qingmei@tju.edu.cn; 吴林键, 通信作者, 博士研究生, 主要从事海工结构动力学, 港口、海岸、近海及海洋工程结构设计理论和方法方面的研究, E-mail: wljabgf@126.com