基于精密三角高程的高寒地区高铁路基冻胀监测

高山，吴会军，刘丹妮，郭江涛

(1.西南交通大学 地球科学与环境工程学院，四川 成都 611756；2.四川西南交大铁路发展有限公司，四川 成都 610072)

基于精密三角高程的高寒地区高铁路基冻胀监测

高山1，吴会军1，刘丹妮2，郭江涛1

(1.西南交通大学 地球科学与环境工程学院，四川 成都 611756；2.四川西南交大铁路发展有限公司，四川 成都 610072)

为了提高高寒地区高速铁路路基冻胀监测的效率和自动化程度，提出基于测量机器人的精密三角高程冻胀监测的方法。通过对三角高程测量的原理和精度分析，采用短测距单向观测的监测方案，优化监测网型，利用相邻高差差分法构建三角高程网的几何模型。在顾及间接高差相关性的前提下根据其协因数阵进行定权，以此开发集冻胀监测数据处理和分析于一体的软件系统。实验验证基于精密三角高程冻胀监测的方法是可行的，使用0.5″的TS30全站仪在气温不低于-15 ℃时，能够达到二等水准测量的精度要求，在不低于-25 ℃的条件下能达到精密水准测量的精度。

冻胀监测；三角高程；精度分析；相关性；CPIII控制点

我国是一个冻土大国，季节冻土区分布面积约占全国陆地面积的53.5%[1]。在季节冻土区修建高速铁路的关键问题之一是路基的冻胀融沉。不均匀路基冻胀融沉对轨道平顺性造成影响，从而影响列车运行的舒适性，严重时会影响列车运行的效率和安全。采用科学有效的方法对路基的冻胀融沉变形进行及时准确的监测可为有关部门提供相应的参考。目前，我国在东北地区修建的哈大和盘营等高速铁路，拟建的北京至莫斯科高速铁路，均面临着路基冻胀融沉的考验。控制冻胀融沉变形并对其进行有效的监测对我国高铁走出去具有重要的意义。为了控制冻害的发生发展，我国采取了一系列的措施来控制冻胀融沉变形并取得了显著的效果。冻胀融沉监测主要采用的是人工水准测量[2]和在路基中埋设冻胀计等传感器自动监测[3]的方法，这2种方法各有优缺点：水准测量相对较灵活，但自动化程度和效率较低；埋设冻胀计的方法测量精度和自动化程度较高，但传感器埋设适宜于高铁建设时期，对于运营开通后的铁路埋设极为不便。三角高程测量是高程测量的一种方法，具有不受地形起伏的限制、测距长、测量速度快等优点。随着高精度测量机器人的出现，测量的效率和自动化程度更是有了显著的提高。许多学者研究基于测量机器人的精密三角高程测量代替高等级水准测量的可行性：张正禄等[4]验证了采用TCA2003全站仪在观测9个测回且距离不大于600 m时，精密三角高程测量能达到一等水准测量的精度要求；刘成龙等[5]提出利用CPIII测量数据构建的三角高程网经平差计算后能达到二等水准测量的精度。然而，在高寒低温的苛刻条件下，基于测量机器人的精密三角高程测量能否进行并能达到何种要求还鲜有报道，这对于冻胀监测技术的发展具有重要推动作用。

1 三角高程测原理及误差分析

1.1 单向三角高程测量原理及精度分析

传统单向三角高程测量是在测站点上分别安置仪器和棱镜，根据测站点向照准点所观测的高度角和斜距，利用三角高程测量公式计算2点之间的高差如图1所示，其公式[6]为：

hAB=Ssinα+i-v+q+f

(1)

其中：

q=(Scosα)2/(2R)

(2)

f=-k(Scosα)2/(2R)

(3)

在公式(1)～(3)中： S为A和B2点之间的斜距；α为高度角； i和v分别为仪器高和棱镜高；q为地球曲率影响值；f大气折光影响值；k为大气折光系数；R为地球半径。

(4)

(5)

式(4)中，仪器高和觇标高丈量误差较小时约为mi=mv=0.3 mm，这对于精密三角高程测量不可忽略。公式(5)中，当S小于1 000 m时，mq小于1×10-3mm，在此情况下地球曲率误差mq可忽略不计。大气折光误差mf的影响在下文详细说明。

将公式(4)中的第1项和第2项分别开平方根，其值分别为测距中误差和测角中误差对高差中误差的影响。TS30全站仪的测距精度为1 mm+1 mm/km，测角精度为0.5″，当对应不同的角度和距离时，其值计算如表1～2所示。

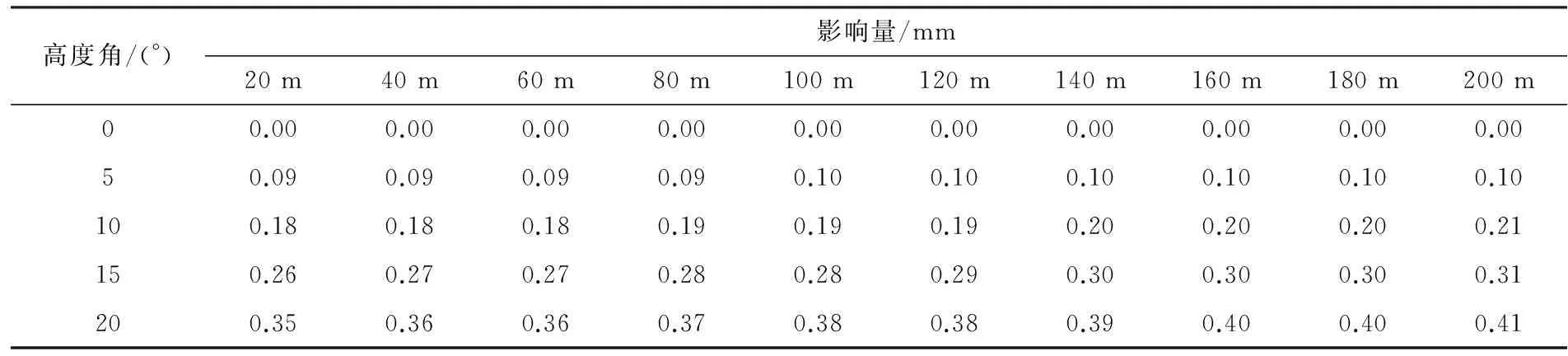
表1 测距中误差对高差中误差的影响Table 1 Mean square error of ranging on elevation difference error

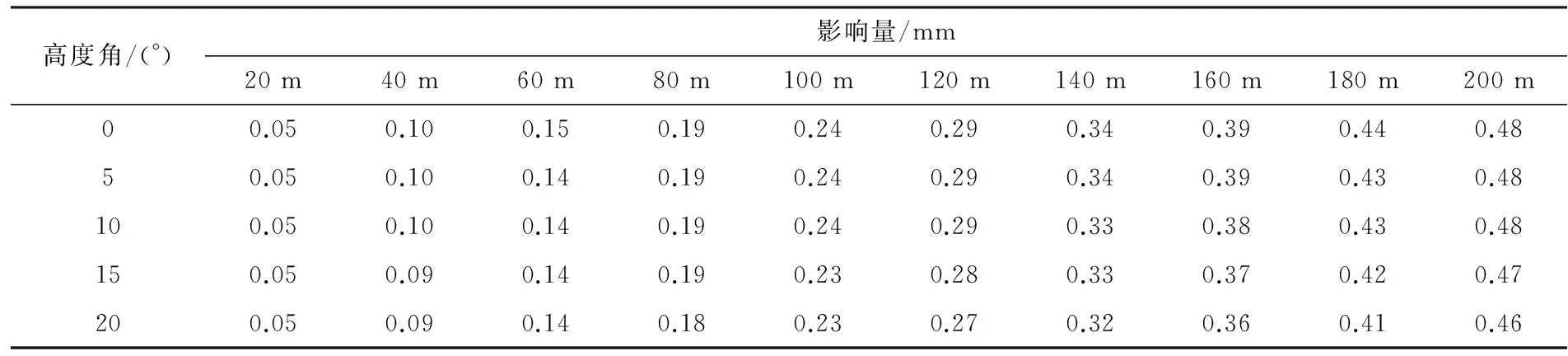
表2 测角中误差对高差中误差的影响Table 2 Mean square error of angle observation on elevation difference error

由表1可以看出，测距中误差对高差中误差的影响随高度角的增大而迅速增大；由表2可以看出，测角误差对高差中误差的影响随距离的增长而迅速增大，因此当高差确定时需要合理的控制高度角和斜距的关系使高差精度更优。

现只分析测角中误差和测距中误差对高差中误差的影响[8]，则其关系公式为：

(6)

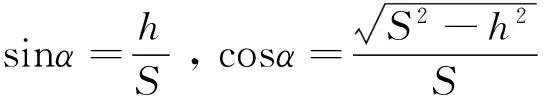
(7)

(8)

驻点对应极小值点。当已知高差和仪器的标称精度时，代入式(8)可以算得高差中误差最小时的斜距值。由于高铁路基上的测站点至监测点的高差基本固定，取h=1.5 m，mα=0.5″，mS=1.1 mm，代入计算得S≈26 m。

将式(7)开平方根，即为高差中误差。将高差中误差表示成斜距S的函数，取h=1.5 m时函数绘图表示如图2所示。

图2 高差中误差变化曲线图Fig.2 Graph of mean square error of elevation difference

图2为斜距从3～200 m时的高差中误差变化曲线。当斜距从3 m增大至26 m时，高差中误差迅速减小，在26 m处取得最小值；当斜距从26 m继续增大时，高差中误差也随之增大，斜距不超过200 m时高差中误差在0.5 mm以内；为使高度角满足《高速铁路工程测量规范》[9]中不超过10°的要求，斜距一般不短于10 m。

1.2 自由设站三角高程测量原理及精度分析

传统单向三角高程测量的高差受仪器高和棱镜度丈量误差的影响。为了提高测量的精度，可采用自由设站的方法[10]，如图3所示，将仪器安置于两测站点之间，在测站点上安置相同高度的棱镜，此时计算两点之间的高差时，不需要量取仪器高和棱镜高，剔除了量高误差。因为大气折光系数k是一动态变量，与空气密度、温度、气压、下覆地物等因素有关，其准确值不易确定，对于距离较长的精密三角高程测量常常采用对向观测[11]或k值反演[12]的方法来尽量削弱大气折光误差的影响。而自由设站三角高程的高差公式为：

hAB=(SOBsinαOB-SOAsinαOA)+(qOB-qOA)+

(fOB-fOA)

(9)

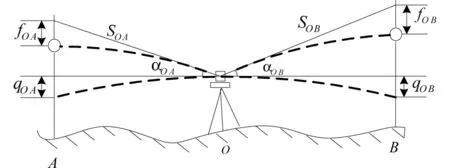
图3 自由设站三角高程测量原理示意图Fig.3 Schematic diagram of the principle of free station-type trigonometric leveling

自由设站三角高程前后视的大气折光系数是一个相关的变量，需化简成独立形式才能应用误差传播定律。其误差包括2个部分，一部分是测区平均折光系数与理想折光系数的误差，一部分是大气状态的动态随机成分影响的误差，用Δk表示。令前后视大气折光变化的差值为Δk=kOB-kOA，将其代入式(3)和(9)后整理为：

(10)

由于自由设站三角高差的各观测量间是独立的，对公式(10)进行全微分后，运用误差传播定律计算可得高差中误差计算公式：

(11)

(12)

(13)

(14)

(15)

令ΔD=SOBcosαOB-SOAcosαOA则公式(14)转化为：

(16)

由公式(16)可以看出：当自由设站三角高程的前后视线越长且视距差越大时，大气折光对高差中误差的影响越大。

三角高程冻胀监测的测量时间一般是在夜晚进行，此时相同和相邻测站的空气密度、温度、气压的变化一般极小，观测视线下的路基起伏情况及表面覆盖物基本一致，这对大气折光的影响也基本一致，所以和mk相比，mΔk应该是一个极小的值。假设mΔk的最大值为mΔk=0.02，当SOB=200 m时，计算mΔf不超过0.06 mm。

大气折光系数取测区平均折光系数k=0.14，大气折光系数中误差取mk=±0.04[12]，ρ=206 265，R=6 371 km，当平距之和400 m，平距之差ΔD为30 m时，计算得mf≈0.04 mm，其对高差的影响可忽略不计。由此可见，对于自由设站的短距离精密三角高程冻胀监测，用测区平均折光系数进行改正时对高差影响不大，其高差中误差的公式化简为：

(17)

2 三角高程冻胀监测的关键问题处理

2.1 三角高程网几何模型

监测网型的布设应该同时兼顾测量的精度和效率，同时还要具备一定的粗差探测能力。高速铁路路基表面宽度一般在10～20 m，其冻胀监测点一般成对布设于两侧的路基上。为了更好地监测冻胀变形对路基纵向平顺性的影响，纵相邻监测点的间距一般不超过30 m，此时同一测站前后各观测4对监测点时测站点至监测点的距离约为16，45，75和105 m，而冻胀监测的精度最优距离在26 m左右，此时采用与相邻测站的测距长短结合的方法，相邻测站重复观测4对监测点，则监测点距离就变成了16和105，45和75 m的组合，从而形成短距离高差保证精度、长距离高差进行检核的形式，网型如图4所示。

对于特殊监测地区，纵向相邻监测点间距应重新设置。在路涵过渡段应要在涵洞顶和涵洞两侧外5～10 m的位置布设监测点。对于重点监测段落，要布设加密监测点，纵向相邻监测点间距为10 m，此时将全站仪置于正对它的一对监测点，此对监测点由其前后相邻的2个测站监测。当同一测站前后各观测4对监测点、相邻测站重复观测4对监测点时的测站网型图如图5所示。

图4 测点间距30 m的监测网型示意图Fig.4 Schematic diagram of monitoring network of 30 m point interval

图5 测点间距10 m的监测网型示意图Fig.5 Schematic diagram of monitoring network of 10 m point interval

2.2 三角高程网平差模型

测站点至监测点的高差为直接高差，将相邻点的高差差分处理，则就形成了间接高差。相邻间接高差为相关观测值，在平差计算时应顾及它们之间的相关性，其关键问题是要得到间接高差的相关权阵。

相关权阵应以测站为单位，不同的测站构成分块矩阵。根据协方差传播率，一测站间接高差的协方差计算公式为：

DBB=ADAAAT

(18)

其中：A为转换矩阵，由计算间接高差的系数阵构成；DAA为直接高差的先验方差矩阵。

则相关权阵公式为：

(19)

只有当DBB为非奇异矩阵时才能通过协因数阵求逆算得权阵。设一个测站观测2n(n≥2)个监测点，则有2n个直接高差，当顾及间接高差的相关性时最多只能构造(2n-1)个线性无关的间接高差，此时能构造的间接高差数量较少。当忽略纵向相邻间接高差的相关性，可构造(3n-3)个间接高差，构造的间接高差网型图如图6所示。

在图6中，以相邻的“纵—横—纵”向间接高差为一个单元，只顾及单元内相邻高差的相关性，则在一个测站中，共有(n-1)个分块矩阵，这(n-1)个分块权阵构成了一个测站的权阵，所有测站的权阵构成了法方程的权阵。

经过差分处理的三角高程网，其平差计算采用间接平差计算即可，通过编程开发“基于精密三角高程的冻胀监测数据处理系统”软件可用于平差计算和冻胀分析。

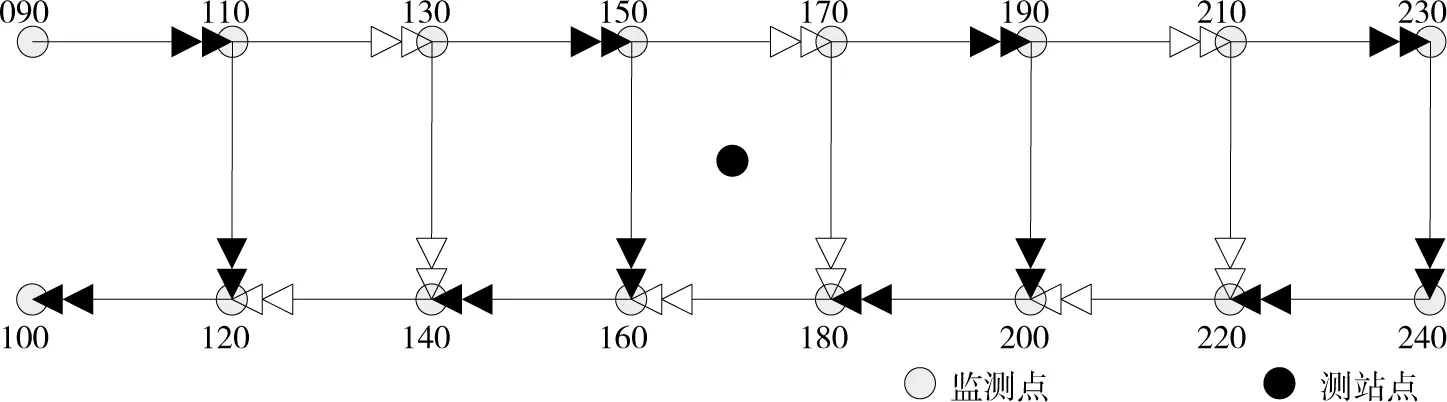
图6 差分后间接高差网型图Fig.6 Schematic diagram of indirect height with differential method

3 冻胀监测实例分析

3.1 外业数据获取

以哈齐客专的某500 m试验段为监测对象，研究精密三角高程冻胀监测的可行性。2014年11月之前完成监测标志布设工作。监测标志采用普罗米新公司生产的预埋件和球棱镜。球棱镜和预埋件的球形凹槽紧密贴合，并通过强力磁铁的吸引而消除了棱镜的对中、安装误差。当在右线轨道板上方安置全站仪时，将左线监测点布设在路肩的边缘，右线监测点布设在路肩中部，如图7所示。按照规定间距总共布设了33对监测点。

图7 冻胀监测视线剖面图Fig.7 Profile of sight of frost heaving monitoring

冻胀监测应选择稳定可靠的已知点作为高程计算的起算点。高速铁路纵向相邻CPIII点的间距为50～70 m，CPIII点数量较多且其高程已知；路基CPIII点位于接触网扩大基础，埋深约4 m，通过查询黑龙江气象部门记录的历年季节冻土的最大冻结深度，监测地区的最大冻深不超过3 m，因此CPIII点不受冻胀融沉的影响，可以用作精密三角高程冻胀监测的约束点。CPIII点应定期复测，以避免不均匀工后沉降影响CPIII高程。每测站可联测1～2个CPIII点，以控制误差累计。

黑龙江地区最冷月最低气温低于-20 ℃，为了应对严寒天气的挑战，给全站仪配备耐低温的外接电池，并用发热保温材料进行保护以保证全站仪在低温条件下能正常运行。受低温的影响仪器的测量精度会有所降低，当气温不低于-15 ℃时，采用徕卡TS30全站仪观测不少于2个测回，当气温不低于-25 ℃时应观测不少于3个测回。当气温低于-25 ℃时，仪器有时候会出现显示面板不正常的问题，此时不建议测量。冻胀融沉发展过程期的监测频次可7～10 d监测1次。

3.2 数据分析

将2014～2015冻胀融沉期内监测的数据代入已知数据平差处理后，统计其符合路线闭合差均能达到二等水准测量限差的要求。将三角高程测量数据与对应期次的4期二等水准测量数据的高程对比，其高程较差统计如表3所示。为了避免起算数据对高程的影响，三角高程和水准测量使用相同的高程起算基准。

表3 三角高程与二等水准高程较差统计
Table 3 Difference of height between trigonometric leveling and second class leveling

项目高程较差统计高程较差区间/mm[0.0～1.0)[1.0～2.0)[2.0～3.0]监测点点数313152百分比/%94.8%4.5%0.6%

通过表3可以看出：三角高程和二等水准测量高程较差在[0 mm，1 mm)区间的比例为94.8%，即：通过相邻高差差分构网并顾及相关性平差计算的高程与二等水准具有相当的精度。但是，需要指出的仅根据高程较差尚不能从严格意义上确定三角高程冻胀监测就能达到二等水准的精度，还需要按《国家一、二等水准测量规范》[13]的指标要求来进行精度确认。

改造后的网型中存在许多同名高差和闭合环，通过同名高差较差可以算得每千米高差偶然中误差。由于同测站构成的闭合环的高差线性相关，由此计算出的每千米高差全中误差的精度虚高，不予统计。统计测量的其中10期数据的每千米偶然中误差如表4所示。

表4 三角高程每千米高差偶然中误差统计表Table 4 Accident mean square error of elevation difference per kilometer of trigonometric leveling

根据《高速铁路工程测量规范》的规定：二等水准测量的每千米高差偶然中误差限差为1 mm，精密水准测量为2 mm。通过表4可以看出，统计的10期数据中，有8期数据的偶然中误差小于1 mm，达到二等水准测量精度的要求，两期数据的偶然中误差小于2 mm，能满足精密水准测量的要求。查询测量时的气温记录，5～7期的测量时温度低于-20 ℃。说明了高寒地区基于三角高程的冻胀监测最低能达到精密水准测量的精度要求。

3.3 冻胀分析

将初始相邻2 d采集的2期数据取均值作为冻胀变形的基准值，后期采集的数据与初值的差值即为冻胀融沉变形量。将某一断面的典型的冻胀融沉变形用折线图表示如图8所示。

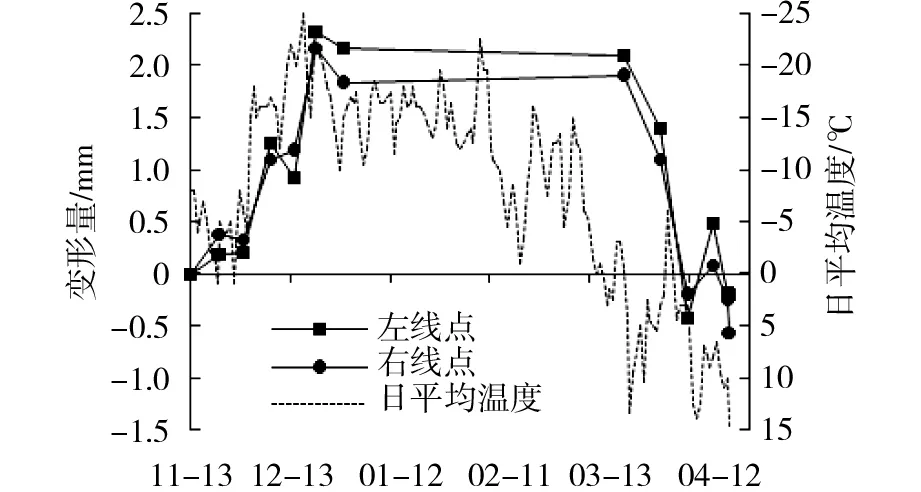
图8 典型冻胀融沉变形折线图Fig.8 Line chart of typical frost heaving and thawing settlement

通过图8可以看出，冻胀期开始后，随着气温的降低冻胀变形量呈直线增大的趋势；当冻深发展到一定程度后，冻胀变形量不再增大。当日均气温升至约0 ℃后融沉期开始，冻胀量开始迅速减小，直到恢复和初值接近的状态，随后保持稳定状态。这和以往得到的冻胀变形规律基本一致。

4 结论

1)分析验证基于测量机器人精密三角高程冻胀监测方法的可行性，采用更加合理的顾及部分间接高差相关性的定权方法；通过平差计算并评定精度，统计规律显示：当温度不低于-15 ℃时能够达到二等水准测量精度的要求，当温度不低于-25 ℃时能够达到精密水准测量精度的要求。

2)和水准测量的方式相比，测量机器人通过自动照准观测提高了外业测量的自动化程度，通过优化监测网型和合理的设站，测量效率也有一定提高；开发的“基于精密三角高程的冻胀监测数据处理系统”软件实现了数据处理和冻胀分析功能，增强了软件的自动化，集成化。

3)基于精密三角高程的测量结果能比较准确地反映冻胀融沉的变化规律，可为高铁路基的优化设计和列车的安全运营提供参考。

[1] 徐学祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2001: 1-2. XU Xuezu, WANG Jiacheng, ZHANG Lixin. Frozen soil physics[M]. Beijing: Science Press, 2001: 1-2.

[2] 石刚强, 赵世运, 李先明, 等. 严寒地区高速铁路路基冻胀变形监测分析[J]. 冰川冻土, 2014, 36(2): 360-368. SHI Gangqiang, ZHAO Shiyun, LI Xianmin, et al. The frost heaving deformation of high-speed railway subgrades in cold regions monitoring and analyzing[J]. Journal of Glaciology and Geocryology, 2014, 36(2): 360-368.

[3] 牛富俊, 刘华, 牛永红, 等. 季节冻土区高速铁路路堑段路基稳定性试验研究[J]. 岩土力学与工程学报, 2013, 32(增2): 4032-4040. NIU Fujun, LIU Hua, NIU Yonghong, et al. Experimental study of roadbed stability in cutting section along a high-speed railway in seasonal frozen regions[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Suppl 2): 4032-4040.

[4] 张正禄, 邓勇, 罗长林, 等. 精密三角高程代替一等水准测量的研究[J]. 武汉大学学报·信息科学版, 2006, 31(1): 5-8. ZHANG Zhenglu, DENG Yong, LUO Changlin, et al.Research on precise trigonometric leveling in place of first class leveling[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 5-8.

[5] 刘成龙, 杨雪峰, 卢建康, 等. 高速铁路CPIII三角高程网构网与平差方法[J]. 西南交通大学学报, 2011, 46(3): 434-450. LIU Chenglong, YANG Xuefeng, LU Jiankang, et al. Construction and adjustment method for CPⅢ trigonometric leveling network of high-speed railway[J]. Journal of Southwest Jiaotong University, 2011, 46(3): 434-450.

[6] 武汉测绘科技大学《测量学》编写组.测量学[M]. 北京:测绘出版社, 2000:267-269. Editing Group for Surveying of Wuhan University of Technology of Surveying and Mapping. Surveying and mapping[M]. Beijing: Surveying and Mapping Press, 2000:267-269.

[7] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社，2009:25-52. Surveying adjustment Subject Group in School of Geodesy and Geomatics, Wuhan University. Error theory and foundation of surveying adjustment[M]. Wuhan: Wuhan University Press, 2009:25-52.

[8] 许国辉. 高精度EDM三角高程测的研究[J]. 测绘通报, 2002(10):22-24. XU Guohui. A study of EDM precise trigonometric leveling[J].Bulletin of Surveying and Mapping, 2002(10):22-24.

[9] TB 10601—2009,高速铁路工程测量规范[S]. TB 10601—2009,Specifications for survey engineering of high speed railway[S].

[10] 郝长春, 高飞, 吴兆福. 自由设站式三角高程测量及应用[J]. 合肥工业大学学报(自然科学版),2010,33(12):1835-1838. HAO Changchun, GAO Fei, WU Zhaofu. Free station-type trigonometric leveling and its application[J]. Journal of Hefei University of technology(Natural Science), 2010, 33(12): 1835-1838.

[11] 郑德华. 精密测距三角高程精度分析及高程混合网定权[J]. 同济大学学报, 2004, 32(4): 507-512. ZHENG Dehua. Accuracy analysis of subtend trigonometric leveling and determination of weight matrix for adjustment of elevation mixed network[J]. Journal of Tongji University, 2004, 32(4): 507-512.

[12] 白少云, 杨琦. 基于MS05AX测量机器人的精密三角高程误差来源于精度分析[J]. 测绘通报, 2015(2):58-63. BAI Shaoyun, YANG Qi. Analysis of errors and precision for precise triangulated height based on MS05AX measuring robots[J]. Bulletin of Surveying and Mapping, 2015(2):58-63.

[13] GB/T 12897—2006,国家一、二等水准测量规范[S]. GB/T 12897—2006, Specifications for the first and second order leveling[S].

The frost heaving monitoring of high-speed railwaysubgrade in cold regions based on precise trigonometric leveling

GAO Shan1，WU Huijun1，LIU Danni2，GUO Jiangtao1

(1.School of Geosciences and Environmental Engineering，Southwest Jiaotong University，Chengdu 611756，China；2.Sichuan Southwest Jiaotong University Railway Development Co.Ltd，Chengdu 610072，China)

In order to improve the efficiency of frost heaving monitoring on high-speed railway subgrade in cold regions，a method of frost heaving monitoring based on precise trigonometric leveling was proposed in this paper. By analyzing the principle and precision of trigonometric leveling，a monitoring program of short-distance and one-way observation was adopted. Monitoring network was optimized and the geometric model of trigonometric network was built by differential method of adjacent height. The weight matrix was determined according to the cofactor matrix considering the correlation of indirect height. A software system that can be used to analyse the frost heaving monitoring data was developed based on these factors. The experiment proves that the frost heaving monitoring based on precise trigonometric leveling is feasible. It can meet the precision acquirement of the second leveling survey when the temperature is no lower than -15 ℃ and the precise leveling survey when the temperature is no lower than -25 ℃ by using the total station TS30 whose angle measurement precision is 0.5″.

frost heaving monitoring; trigonometric leveling; precision analysis; correlation; CPIII control points

2016-01-23

中国铁路总公司科研试验项目(Z2013-038-5)；四川省交通科技项目(2012C2-1)

高山(1975-)，男，重庆人，副教授，博士，从事精密工程测量与变形监测研究；E-mail: samgau@home. swjtu.edu.cn

P224.2

A

1672-7029(2016)12-2360-08