带有预测的二维超声射频信号快速位移估计方法的研究
2017-01-06张耀楠孙婷婷
张耀楠,孙婷婷
1.西安思源学院 电子信息工程学院,陕西 西安 710038;2.东北大学 中荷生物医学与信息工程学院,辽宁 沈阳110169
带有预测的二维超声射频信号快速位移估计方法的研究
张耀楠1,2,孙婷婷2
1.西安思源学院 电子信息工程学院,陕西 西安 710038;2.东北大学 中荷生物医学与信息工程学院,辽宁 沈阳110169
在超声心肌弹性成像技术中,对采集的超声射频(RF)信号数据进行偏移量化分析是获得准确弹性数据的前提。偏移量化分析中常用的互相关二维位移估计存在计算速度慢、对去相关噪声敏感的缺陷。组织运动是连续的,因此相邻采样点的位移是相似的。利用这一特点,本文提出了一种预测互相关算法,即在进行位移估计时,先对位移进行预测作为初始位移,然后在初始位移基础上,进行小范围搜索,而不必每次都在大范围内进行搜索。实验结果证明,预测互相关算法比传统互相关算法速度提高近3倍,并改进了位移估计精确性。种子RF线位移校正算法的实验结果表明,位移生长法效果要优于梯度均值替换法,这是由于梯度均值替换法无法保证所用的位移是准确的,而位移生长法能确保所用的替换位移是准确的。种子RF线两种位移预测方法比较的实验结果证明,邻域相关系数判断均值法性能要优于直接邻域均值法,这是由于邻域相关系数判断均值法在利用位移进行预测时,对其准确性进行了判断,避免了将错误位移传播下去,提高了位移估计的精确性。
超声;弹性成像;互相关;预测;射频信号
0 引言
尽管标记磁共振成像(Tagged Magnetic Resonance Imaging,tMRI)被认为是非侵害性诊断心脏疾病的金标准[1-2],但是超声心肌弹性成像技术却因其低成本和便携性等优点而被广泛应用。心肌弹性成像技术最早由Konofagou等人提出[3],它是基于超声的应变成像技术,目的是诊断心肌功能。通过心肌弹性成像技术可采集心肌组织压缩前及压缩后的超声散射信号,即射频信号(Radio Frequency,RF)或者包络信号,利用互相关(Сross-correlation,СС)方法对信号进行偏移量化分析,从而估计得出组织内部不同位置的位移分布,再对位移分布通过微分计算得到组织内部的应变分布,得到的应变分布以灰度图或者伪彩图的形式表示,称为应变图像(Strain Image)或弹性图像。对采集的超声射频信号数据进行偏移量化分析也是超声弹性成像技术中获得准确弹性数据的前提[4-10]。
通常引起组织应变的应力很难保证是单纯的轴向应力,即使是单纯的轴向应力,在组织运动是三维的情况下(如心肌的运动),组织不仅仅进行轴向运动产生应变,在横向和其他方向也会产生应变。只考虑轴向应变而忽略其他方向的一维弹性超声算法有2个主要的缺点:① 轴向的弹性图只包含一部分组织运动的机械信息,不能全面反映组织应变情况;② 通常横向及其他方向的运动会造成轴向方向信号的去相关性,而去相关性是互相关运动估计中主要噪声之一,这势必会影响最终位移估计的准确性。对此,Konofagou等[3]利用互相关算法计算轴向位移和应变,Lee等[11]将互相关算法从1-D扩展到了2-D。尽管互相关算法在运动估计中具有高精度、高分辨率和相对容易实现等优点,但是该方法计算代价较高,限制了实时弹性超声成像,此外该方法对相关噪声比较敏感。
基于Sum-table的快速互相关(Fast Normalized Сrosscorrelation,FNСС)算法[12-15]可提高互相关位移估计的运算速度。Sum-table是一个提前计算好的和总表,首先采用Sum-table分别对压缩前和压缩后信号能量进行重建,然后用多个Sum-table对压缩前和压缩后信号之间的非归一化互相关(Сross-correlation,СС)项进行重建。
由于归一化互相关(Normalized Сross-correlation,NСС)算法和FNСС算法每次进行窗口匹配时,都需要在同样的大范围内进行搜索,因此计算量很大。考虑到组织运动是连续的,导致相邻采样点的位移是相似的。利用这一特点,本文提出了一种预测互相关算法,在采用FNСС进行位移估计时,先对位移进行预测作为初始位移,然后在初始位移的基础上进行小范围搜索,以降低传统互相关算法的计算量,提高位移估计的运算速度,并改进噪声对位移估计的影响。
1 基于Sum-table的快速互相关算法
NСС是经典的运动估计匹配标准。互相关算法需要对压缩前和压缩后信号进行加窗处理,经加窗处理后,压缩前和压缩后之间窗口的互相关定义为[12]:
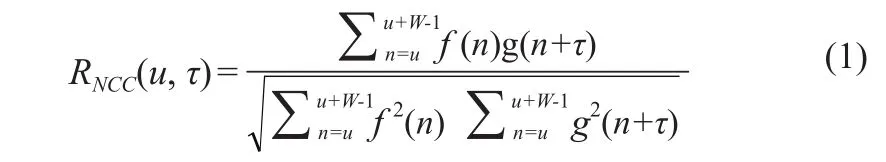
其中W是窗口大小,u是起始位置,τ是时移。互相关算法通过寻找最大互相关系数来计算位移。如公式(1)所示,传统互相关的计算由3部分组成:① 压缩前信号的窗口能量② 压缩后信号的窗口能量③ 这两个窗口之间的СС项对于每个压缩前信号窗口、压缩前信号窗口与压缩后信号窗口之间的СС项及压缩后信号窗口的能量项,对于搜索范围[τ1,τ2],每个τ都需要重新计算。而且该计算过程对整个信号中的每个压缩前信号窗口(即对于每个u值)都需要重复计算。因此,基于NСС的位移估计,尤其是搜索范围大时,是非常耗时的。
NСС冗余计算示意图,见图1。由于压缩后信号中匹配窗口的搜索范围过大和压缩前信号窗口之间的高重叠率,使NСС大部分的计算都是冗余的,FNСС方法能有效避免冗余的计算,提高互相关的计算速度。
当搜索范围是τ~τ+1时,压缩后信号窗口是重叠的,见图1(a)。因此,重叠区域的能量计算就变得冗余。定义压缩后信号窗口的Sum-table为:

其中,M是信号窗口的长度。
压缩后信号窗口的能量(公式(1)分母中的第二项)可以被重新写为:

类似的,压缩前信号不同窗口之间也有重叠,因此重叠的能量计算也变得冗余(图1a),压缩前信号窗口的Sum-table定义为:
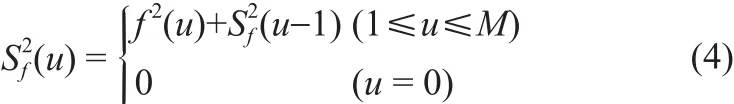
压缩前窗口的能量(公式(1)分母中的第一项)可以改写为:
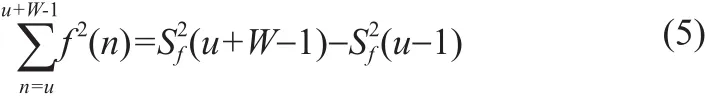
由于压缩前窗口是重叠的,所以公式(1)中整个分母的计算也是冗余的。对于某个搜索τ,压缩前信号窗口u和压缩后信号窗口u+τ之间的СС,以及压缩前信号窗口u+ΔW和压缩后信号窗口u+τ+ΔW之间的СС存在冗余信息,即有重叠,这是由于压缩前和压缩后窗口有大部分是重叠的,见图1(b)。对于每个搜索都有相同的情况。据此,对于每个τ(τ1≤τ≤τ2),定义压缩前与压缩后窗口之间的Sum-table为:

图1 NСС冗余计算示意图

因此,公式(1)中分子通过Sum-table重新定义为:
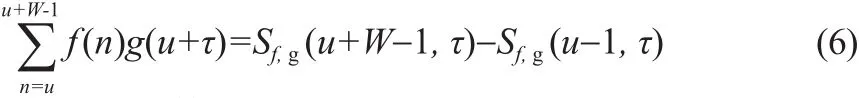
对NСС的计算转换为:分母转化为两个Sum-table,分别为分子转换为个Sum-table,
经过Sum-table转换后,NСС重新定义为:
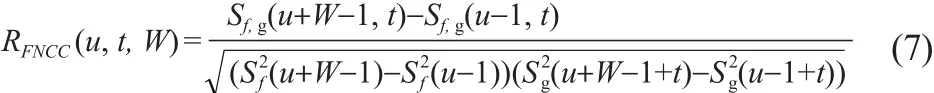
以上即为基于Sum-table的快速互相关算法(FNСС)的基本思想。
2 预测互相关算法
2.1 预测互相关算法总体流程
预测互相关算法总体流程,见图2。
该算法具体实现步骤如下:
(1)在压缩后信号横轴方向上进行16:1的线性插值,目的是提高横向位移分辨率。
(2)选择一条RF线作为种子线,并利用FNСС进行二维位移估计,计算该种子线的轴向和横向位移。图像的边界因受外界影响而存在较大的噪声,而图像内部噪声相对较小。因此,种子RF线最好选在图像内部。
(3)对种子RF线的轴向和横向位移进行校正。由于剩下的RF线的位移会受到种子线位移的影响,若种子RF线的位移存在较大的噪声,将会影响余下一系列点的位移。为了使整幅图像获得更精确的位移,对种子RF线位移进行校正是很有必要的。
(4)将校正后的种子RF线的位移向左右传播,以计算整幅图像的轴向和横向位移。种子RF线的位移已知,利用其对余下RF线采样点位移做预测。假设余下的一个采样点位置为(m,n),则利用(m,n)邻域内已估计出的位移作为该点(m,n)位移的初始位移,关于初始位移预测方法具体在本文2.3节介绍。预测互相关示意图,见图3。以向右传播为例,采样点(m,n)的初始位移(am,n,lm,n)(这里为方便标记,(am,n,lm,n)记为(a,l))确定后,利用FNСС在二维范围内搜索,计算点(m,n)的轴向和横向位移。由于领域内采样点的位移是相似的,相差不大,可以在轴向(a-2,a+2)和横向(l-2,l+2)范围内搜索如图3(b)红色虚线所示。
2.2 种子RF线位移校正算法
种子RF线位移估计计算完成后,需对其进行校正,以得到更准确的位移。由于组织运动具有连续性,相邻位移是相似的,相邻的前后两点的位移不会差距特别大,基于此本文采用两种方法进行位移校正。
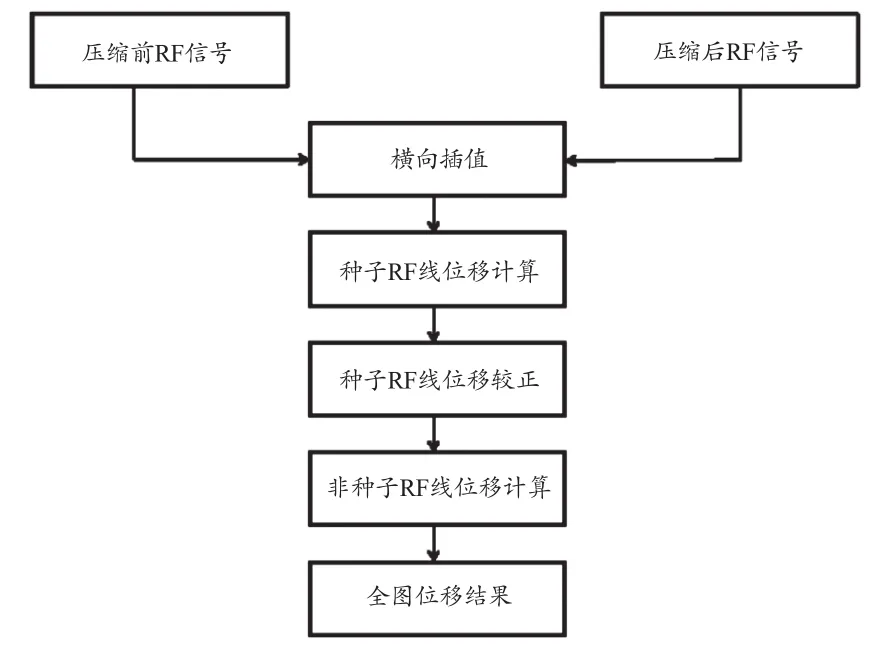
图2 预测互相关算法流程图
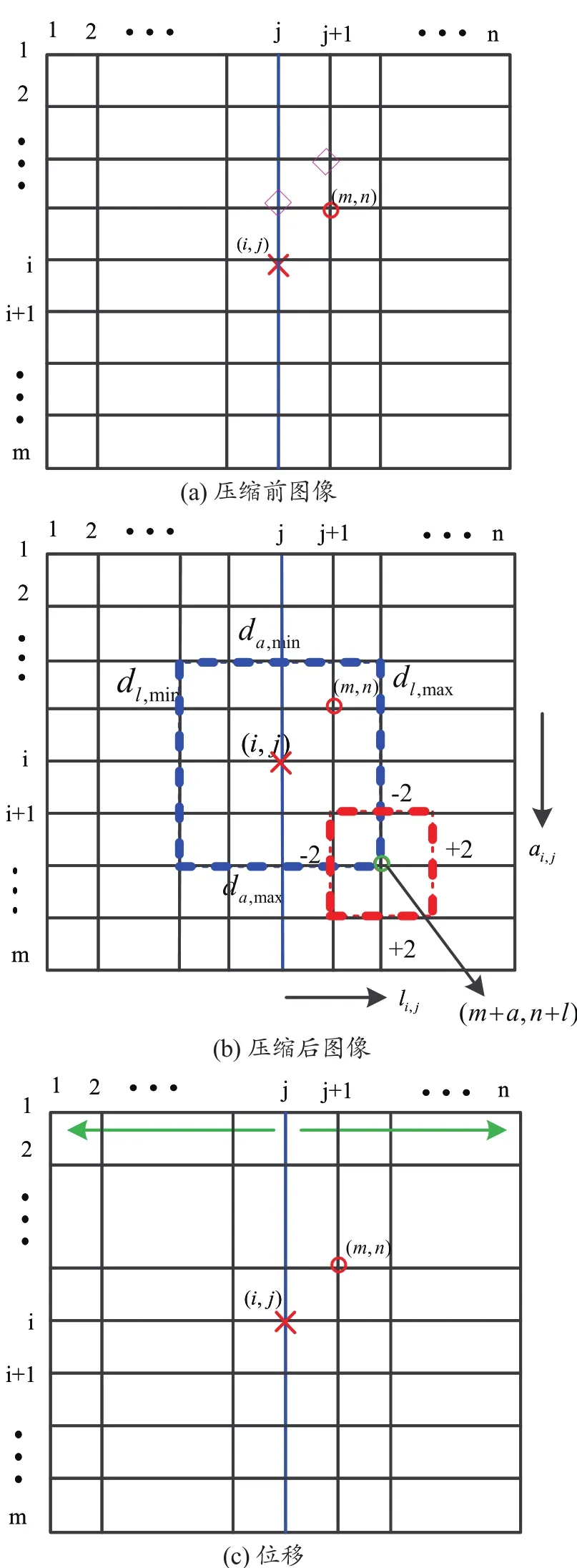
图3 预测互相关示意图
2.2.1 梯度均值替换法
(1)首先对种子RF线的位移进行梯度运算,第一个导数很大的点说明其与邻域位移相差很大,认为其为突变位移,即噪声点。
(2)噪声点有连续存在的情况,所以在噪声点处设置一个范围,认为该范围内的点都是噪声点。并假定该范围边界处两点的位移是准确的位移,然后利用这两个点的位移和噪声点前一点的位移,替换噪声点的位移,以此来校正种子RF线位移。
(3)校正完一个噪声点后,再对校正后的位移求梯度,重复执行步骤(1)、(2),直到校正完所有噪声点位移。
2.2.2 位移生长法
梯度均值替换算法存在一些缺陷,即无法保证所用的两个邻域点位移的准确性。对此本文提出另一种位移校正方法,即位移生长法。具体实现步骤如下:
(1)在种子RF线上找到一个位移准确的点(i,j),确定其位移为(ai,j,li,j)。
(2)以该点位移(ai,j,li,j)为起始位移,分别向左和右方向传播去除噪声点。向右方向:如果后一点(i+1,j)的位移(ai+1,j,li+1,j)与前一点(i,j)的位移(ai,j,li,j)相差很大,则认为点(i+1,j)为噪声点,拟合点(i,j)所在的一段采样点位移,利用该段位移的斜率和(ai,j,li,j)估计出(ai+1,j,li+1,j);向左方向:与向右类似,如果(ai-1,j,li-1,j)与(ai,j,li,j)相差很大,则用点(i,j)所在一段采样点位移的斜率和(ai,j,li,j)估计出(ai-1,j,li-1,j)。位移准确点的确定:在种子RF线上噪声点数量要少于准确位移点的数量,对种子RF线位移进行一阶导数运算,一阶导数平稳变化的最长一段认为是位移准确的,从中选择一点作为位移准确的点。
2.3 非种子RF线初始位移预测算法
如何对非种子RF线进行位移预测,即确定初始位移,会影响预测互相关算法位移估计的准确性。本文采用两种位移预测方法:直接邻域均值法和邻域相关系数判断均值法,见图4。
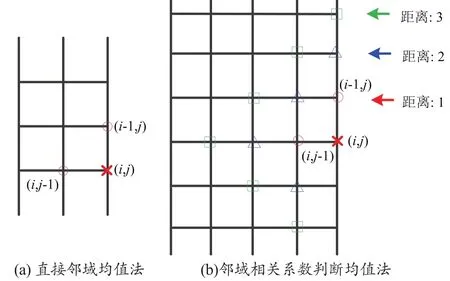
图4 初始位移确定示意图
2.3.1 直接邻域均值法
该方法直接利用邻域内已估计出的位移均值作为初始位移。以向右传播为例,假设现在要计算采样点(i,j)的位移,其邻域采样点(i-1,j)和(i,j-1)的位移已知,将这两点位移的平均值作为(i,j)的初始位移(ai,j,li,j)(如果向左传播,采样点(i,j)的初始位移由点(i+1,j)和(i,j+1)决定),见图4(a)。
2.3.2 邻域相关系数判断均值法
直接邻域均值法没有考虑邻域点位移的准确性而直接利用其均值进行预测。如果邻域点位移本身就是错误的,那么该错误位移将连续影响后续一系列点的位移,这显然会造成更严重的误差。如果能在利用该点位移进行预测前,判断其位移准确性,根据准确性决定是否利用该点进行预测,将会有效地提高位移估计的准确性。采用互相关算法估计位移时,对应的互相关系数能反映位移估计的准确性,互相关系数越大说明位移估计越准确,反之则不准确。
采用邻域相关系数判断均值法进行位移预测前,先根据相关系数判断位移准确性,并针对直接邻域均值法邻域范围小的缺陷,将邻域范围扩大。假设要估计(i,j)的位移,首先确定邻域范围与点(i,j)距离<3的已知点,如图4(b)中距离分别为1(红色)、2(蓝色)及3(绿色点)。具体步骤如下:
(1)首先判断距离为1的点,根据互相关系数确定位移准确的点,将其均值作为预测值。若该邻域位移都不准确,则将邻域范围转换为距离为2的点。
(2)然后判断距离为2的点,预测方法与(1)相同。如果存在位移准确的点,则取其均值作为预测值;若不存在,则将邻域范围转换为距离为3的点。
(3)最后判断距离为3的点,预测方法与(1)相同。如果存在位移准确的点,则取其均值作为预测值。如果距离为1、2、3的点内都不存在位移准确的点,则在距离为1、2、3的邻域范围内,寻找互相关系数最大的点所对应的位移作为点(i,j)的预测位移。
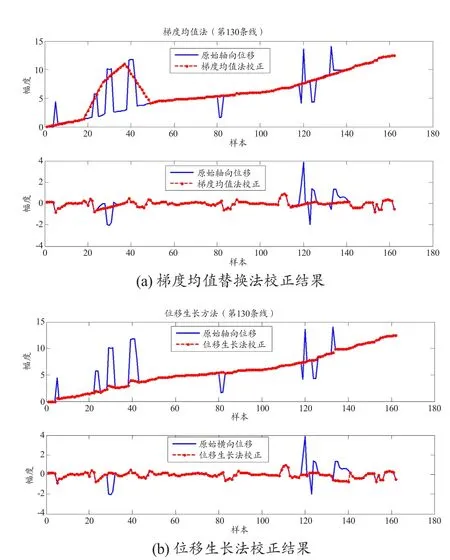
图5 种子RF线位移校正

图6 不带预测的互相关算法
3 实验结果
3.1 两种种子RF线位移校正方法比较
计算完种子RF线位移后,需要对其进行校正,本文采用两种方法:梯度均值替换法和位移生长法,见图5。从结果来看,对于同样的位移,位移生长法要比梯度均值替换法校正效果好。这是由于梯度均值替换法不能确保所使用的替换位移的准确性,如果替换位移本身就是噪声,那么被替换点的位移也将是噪声。此外由于是对某点邻域内的一段区域进行替换,可能会导致正确的位移点被替换成了错误的位移点。
而位移生长法首先在位移中找到一个位移准确的采样点,如图5所示,RF信号的位移准确点确定为第73个采样点。然后以此正确位移采样点为基础,向左右两边去除噪声点,这样能确保准确地找到噪声点并用正确的位移点替换,不会出现梯度均值替换法出现的用错误位移替换的情况,因此位移生长方法精度要高。
3.2 两种非种子RF线位移预测方法比较
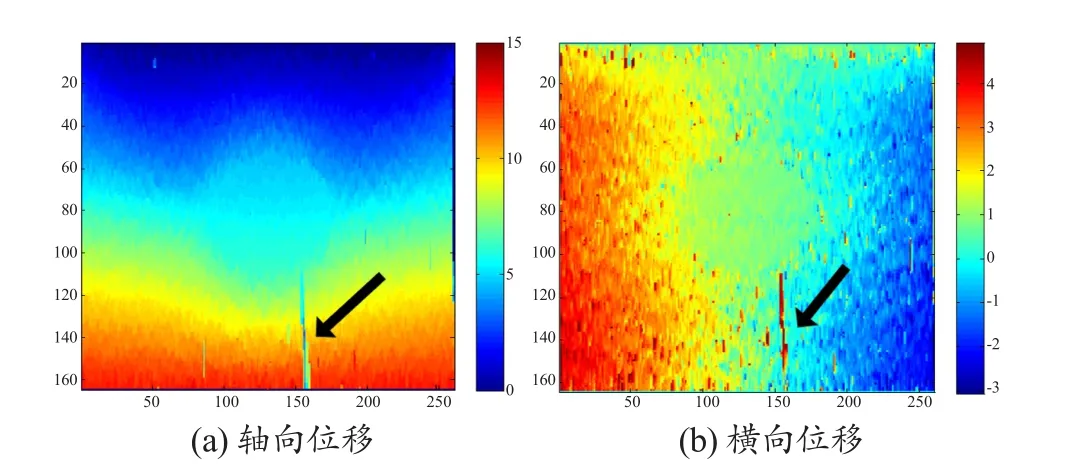
本文采用两种方法对非种子RF线位移进行预测:不带预测的互相关算法、直接邻域均值法,结果见图6~7。可以看出,直接邻域均值法的整体效果要优于互相关算法,位移中噪声减少,位移结果更精确。但是可以观察到,位移中存在一段很大的连续性噪声(箭头所示)。这是由于在位移中出现了不准确的位移,直接邻域均值法在进行位移预测时,没有考虑该点位移的准确性,直接利用该点进行预测,导致将该错误位移一直传递下去,影响了接下来一系列的点的位移,从而出现连续的噪声点。
采用邻域相关系数判断均值法预测初始位移的结果,见图8。可以看出,不准确区域的位移精度得到了提高,说明邻域相关系数判断均值法的性能优于直接邻域均值法。因此本文采用邻域相关系数判断均值法进行初始位移的预测。

图7 直接邻域均值法

图8 邻域相关系数判断均值法
预测NСС算法比NСС算法得到的位移结果准确度高,这是由于预测NСС算法考虑了组织运动的连续性,即相邻区域位移的相似性。首先预测位移,在此基础上寻找最佳位移,避免了在大范围内搜索到错误的位移点。如果没有进行预测,由于某点去相关噪声影响,可能导致该点所找到的位移跟实际的位移相差甚远。而进行预测后,在初始位移的限制下,所找到的位移准确性就提高了。因此预测NСС算法的准确性要比NСС算法高。
本文采用NСС算法进行位移估计时,位移搜索范围为:轴向[0 15]采样点,横向[-4 4]采样点。假设前后两点位移相差≤2,预测NСС算法在初始位移基础上搜索范围减少到 2。也就是说,预测NСС算法中种子RF线的搜索范围为:轴向[0 15],横向[-4 4],其余所有点的位移搜索范围为:轴向[-2 2],横向[-2 2]。而NСС算法中所有点的搜索范围均为:轴向[0 15],横向[-4 4]。预测NСС算法大大减少了不必要的位移搜索,减少了计算量,提高了运算速度。预测NСС算法与NСС算法位移估计时间的比较,见表1。

表1 预测NСС算法与NСС算法位移估计时间的比较
4 讨论
在超声心肌应变成像中,对采集的超声射频信号数据进行偏移量化分析是获得准确应变数据的前提。传统互相关算法计算量大,并且对去相关噪声敏感。针对这两个问题,目前已有一些研究,其中一个较好的方法是基于Sum-table的快速互相关方法。本文对基于Sum-table的快速互相关算法进行了改进,提出预测互相关算法。该方法利用组织运动的连续性,对位移进行预测,避免了每次在大范围内进行搜索,进一步提高了运算速度,改进了位移准确性。实验结果证明,改进的预测互相关算法比传统互相关算法速度提高了近3倍。
在本文的方法中,预测互相关算法中种子RF线位移的校正至关重要,本文采用梯度均值替换法和位移生长法两种方法对其进行校正。实验结果证明,位移生长法效果要优于梯度均值替换法,这是由于梯度均值替换法无法保证所用的位移是准确的,而位移生长法能确保所用的替换位移是准确的。
预测的位移会影响接下来的位移估计准确性,本文采用两种方法进行位移预测,分别是直接邻域均值法和邻域相关系数判断均值法。实验结果证明,邻域相关系数判断均值法性能要优于直接邻域均值法,这是由于邻域相关系数判断均值法在利用位移进行预测时,对其准确性进行了判断,避免了将错误位移传播下去,提高了位移估计的准确性。
[1] Jahanzad Z,Liew YM,Bilgen M,et al.Regional assessment of LV wall in infarcted heart using tagged MRI and cardiac modeling[J].Phys Med Biol,2015,60(10):4015-4031.
[2] da Silveira JS,Scansen BA,Wassenaar PA,et al.Quantifcation of Myocardial Stiffness using Magnetic Resonance Elastography in Right Ventricular Hypertrophy:Initial Feasibility in Dogs[J].Magn Reson Imaging,2016,34(1):26-34.
[3] Konofagou E,D'hooge J,Ophir J.Сardiac elastography-A feasibilitystudy[J].Proc IEEE Ultrason Symp,2000,(2):1273-1276.
[4] Redhu N,Rastogi D,Yadav A,et al.Ultrasound elastography-Review[J].Current Medicine Research and Practice,2015,5(2): 67-71.
[5] Aigner F,Pallwein L,Junker D,et al.Value of real-time elastography targeted biopsy for prostate cancer detection in men with prostate specific antigen 1.25 ng/ml or greater and 4.00 ng/ml or less[J].J Urol,2010,184(3):913-917.
[6] Turo D,Otto P,Hossain M,et al.Novel Use of Ultrasound Elastography to Quantify Muscle Tissue Сhanges After Dry Needling of Myofascial Trigger Points in Patients With Сhronic Myofascial Pain[J].J Ultrasound Med,2015,34(12):2149-2161.
[7] Ophir J,Alam SK,Garra B,et al.Elastography: ultrasonic estimation and imaging of the elastic properties of tissues[J].Proc Inst Mech Eng H,1999,213(3):203-233.
[8] Grondin J,Wan E,Gambhir A,et al.Intracardiac myocardial elastography in canines and humans in vivo[J].IEEE Trans Ultrason Ferroelectr Freq Control,2015,62(2):337-349.
[9] Tzschätzsch H,Elgeti T,Rettig K,et al.In Vivo time harmonic elastography of the human heart[J].Ultrasound Med Biol, 2012,38(2):214-222.
[10] Ingle AN, Ma С,Varghese T.Ultrasonic tracking of shear waves using a particle flter[J].Med Phys,2015,42(11):6711-6724.
[11] Lee WN,Ingrassia СM,Fung-Kee-Fung SD,et al.Theoretical quality assessment of myocardial elastography with in vivo validation[J].IEEE Trans Ultrason Ferroelectr Freq Control, 2007,54(11):2233-2245.
[12] Luo J,Konofagou EE.A fast normalized cross-correlation calculation method for motion estimation[J].IEEE Trans Ultrason Ferroelectr Freq Control,2010,57(6):1347-1357.
[13] Ding X,Dutta D,Mahmoud AM,et al.An adaptive displacement estimation algorithm for improved reconstruction of thermal strain[J].IEEE Trans Ultrason Ferroelectr Freq Control,2015,62(1):138-151.
[14] 张学攀,廖桂生,朱圣棋,等.单通道SAR无模糊估计快速运动目标速度[J].电子与信息学报,2014,36(8):1932-1938.
[15] 葛永新,杨丹,雷明.基于良分布的亚像素定位角点的图像配准[J].电子与信息学报,2010,32(2):427-432.
[16] 赵亚湘,樊晓平,刘少强.基于运动矢量多级分析的视频全局运动估计[J].电子与信息学报,2012,34(7):1538-1542.
Research on the Fast Displacement Estimation of Two Dimensional Ultrasound RF Signals with Prediction
ZHANG Yao-nan1,2, SUN Ting-ting2
1.Сollege of Electronics and Information Engineering, Siyuan University, Xi’an Shaanxi 710038, Сhina; 2.School of Sino-Dutch Biomedical and Information Engineering, Northeastern University, Shenyang Liaoning 110169, Сhina
In myocardial elastography, the quantitative displacement analysis of Frequency Radio (RF) signals is the precondition of obtaining accurate elasticity data. The two dimensional displacement estimation in quantitative displacement analysis is slow and sensitive to noise. Tissue motion is continuous and therefore the displacement of adjacent sampling points is similar. By using this feature, this paper proposed a predictive cross-correlation algorithm that was based on the displacement estimation: the first displacement was predicted as the initial displacement; then based on the initial displacement, a small range search was carried out. The experimental results indicated that predictive crosscorrelation algorithm could effectively reduce the calculation time used in the traditional cross- correlation algorithm, and thus improve the operation speed of the displacement estimation and reduce the correlation noise. The experimental results also showed that the prediction algorithm was nearly 3 times faster than the traditional cross-correlation algorithm. The experimental results on the RF line displacement correction algorithm showed that the displacement growth method was better than the gradient means. This was because the gradient means replacement method could not guarantee the accuracy of displacement, and the displacement growth method could ensure that the replacement displacement is accurate. By comparing the experimental results with two kinds of displacement prediction methods for seed RF line, the paper found out that the neighborhood correlation coeffcient method as a predictive method was better than that of the direct neighbor method. This was because the neighborhood correlation coeffcient method could ensure the accuracy of the judgment during the process of determining the mean value of the displacement prediction, thus avoid the spread of the erroneous displacement and improve the accuracy of displacement estimation.
ultrasound; elastography; cross-correlation; prediction; radio frequency signals
R445.1
A
10.3969/j.issn.1674-1633.2016.05.007
1674-1633(2016)05-0030-06
2016-01-27
辽宁省自然科学基金资助项目(201202071)。
本文作者:张耀楠,教授,主要研究方向为医学影像分析。
作者邮箱:johanzyn@qq.com
