大跨径悬索桥反应谱法和时程分析法对比研究

2017-01-05

福建交通科技 2016年6期

(同济大学，上海 200009)

■陈峻

(同济大学，上海 200009)

本文以江阴长江公路悬索桥为工程背景，采用数值模拟的方法对该桥的抗震性能进行了深入的研究。采用现行的抗震设计方法，利用有限元分析软件ANSYS建立了悬索桥计算模型，通过合理模拟该桥的边界条件及初始状态，并结合相关理论，对其动力特性进行了详细的分析，得到了该桥的自振频率及振型；结合现行的抗震规范，利用反应谱法和时程分析法在不同方向地震作用，得到主梁、主塔各关键截面位移及内力动力响应结果，可供类似工程参考借鉴。

悬索桥动力特性反应谱时程分析地震反应

1 前言

随着我国经济的飞速发展，大跨度桥梁的建设如雨后春笋，方兴未艾，悬索桥以其独特的缆索承重特点，超大的跨度，受到设计者的青睐[1]。同时，大跨度悬索桥的结构特性，决定其具有独特的动力特性和抗震性能[2]。目前国内外有许多学者对大跨度悬索桥进行了地震响应的研究[3-6]，但所分析的桥跨度有限，对于超大跨度悬索桥缺乏针对性。

本文以江阴长江公路悬索桥为例，通过合理的假定及简化，利用ANSYS建立了较为精确的整桥有限元模型，并对其自振特性进行了分析；然后，运用反应谱分析方法和时程分析方法分别对该桥进行地震动力响应分析，提取了各关键截面的内力、位移峰值，并结合相关规范对比了以上两种分析方法的计算结果。

2 工程概况

江阴长江公路大桥是中国首座跨径超千米的特大型钢箱梁悬索桥梁，是国家公路主骨架中同江至三亚国道主干线以及北京至上海国道主干线的跨江“咽喉”工程。江阴长江公路大桥位于江苏省江阴市黄田港以东3.2km的西山与靖江市十圩村之间。

江阴长江公路大桥主跨(328+1385+295)=1385m钢箱梁悬索桥，两根主缆直径为0.870m，主梁采用流线型箱梁断面，钢箱梁全宽36.9m，梁高3m，桥面宽29.5m，双向六车道，两侧各设宽1.8m的风嘴。桥塔高190m，为两根钢筋混凝土空心塔柱与三道横梁组成的门式框架结构，重力式锚碇。设计行车速度为100km/h；桥下通航净高为50m，可满足5万吨级轮船通航。江阴长江大桥照片见图1。

图1 江阴长江大桥

3 有限元模型建立

本文采用大型通用有限元程序ANSYS建立江阴长江悬索桥空间模型，如图2所示。全桥采用“脊梁”式空间杆系结构，主缆和吊索采用空间杆单元，主跨及边跨加劲梁采用空间梁单元和刚臂单元模拟，主塔及桩基础均采用空间梁单元，对于主缆和吊索这类柔性构件，计入轴向拉力对刚度的贡献，即用几何刚度阵考虑恒载索力的线性2阶影响[7]。主缆内力与变形的关系是非线性的，其弹性模量用Ernst公式修正，悬索桥主缆通过索鞍架设在主塔顶上，没有相对位移，故主缆与主塔顶建立变位主从关系。悬索桥空间有限元模型见图2。该大跨悬索桥所采用的主要材料是混凝土和钢材。建模具体材料参数见表1。

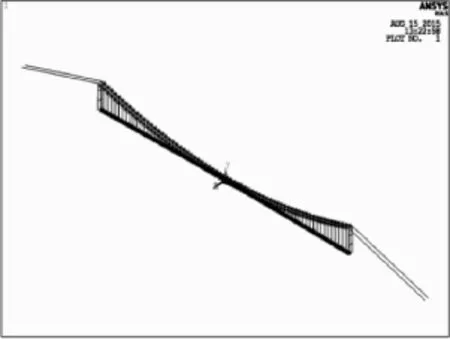
图2 悬索桥空间有限元模型

表1 主要材料参数

4 自振特性分析

对于非线性效应突出的大跨度悬索结构，在动力分析之前，都须进行恒载起点的非线性静力分析，以计入恒载起点的效应及几何非线性效应的影响[8]，根据虚位移原理推得梁单元的切线刚度矩阵，采用Newton-Raphson迭代求解，确定结构在自重下的切线刚度矩阵，然后在此基础上进行动力特性分析和地震响应分析。

结构的主频与振型是结构质量与刚度分布的反映，是研究悬索桥动荷载行为的基础。在ANSYS中用兰索斯(Lanczos)向量法求解模态特征值和特征向量，悬索桥前10阶振型参数表见表2，前5阶振型图如图3所示。

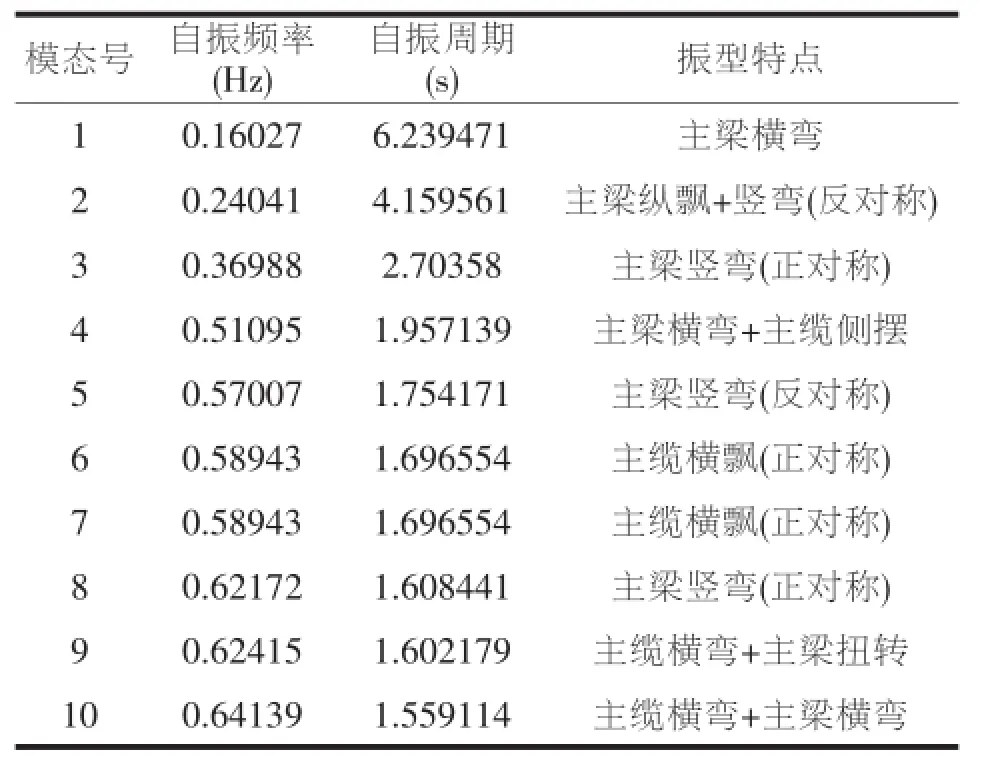
表2 悬索桥前10阶自振振型参数表

图3 前5阶自振振型图

根据以上自振振型计算结果可知，该悬索桥模型的第1阶振型为主梁横弯，符合悬索桥的受力特点，同时与现有大多数同类悬索桥的振型特征相似。同时本桥的自振频率较密集，因此在较小的范围内许多振型可能被激起，加大了发生振型叠加几率，对于主梁的耦合研究应该予以重视。

悬索桥的自振振型从低到高依次为横飘、主梁纵飘+竖弯(反对称)、主梁1阶竖弯、主梁1阶横向、主梁2阶竖弯、主缆振动，说明桥梁振型排列合理，悬索桥1阶扭转频率为1阶竖向频率的2.33倍，证明悬索桥具有很好的抗风稳定性。由于本桥加劲梁跨度很大，又为悬吊体系，因此以加劲梁振动为主的频率均很低，本桥前5阶均是以主梁的振动为主振型。以主塔为主的振型出现的较早，出现在第8阶，说明主塔受地震反应较大，是后续抗震分析的重点。

5 地震响应分析

5.1 反应谱分析结果

由《公路桥梁抗震设计细则》(JTG/B02-01-2008)[9]可知，对于不同的桥梁结构形式考虑的地震作用不同：

(1)对于一般的公路桥梁，仅需考虑水平地震作用，直线桥还需加上纵向地震作用。

(2)对于一些构造形式特殊、跨径较大的桥梁，在抗震设防烈度为8度以上时，需同时考虑三个方向的地震作用。

本文计算的结构为大跨径悬索桥，属于第二类桥梁，故需同时考虑三向地震力的作用，按地震作用三向分量组合进行计算，先分别单独考虑单向地震力作用下的受力响应，再由式(1)进行受力效应组合，求得三向地震作用下的受力响应E。

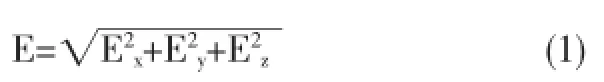
式中：Ex为纵向受力响应,Ey为竖向受力响应,Ez为横向受力响应。

该大跨径悬索桥所在场地为Ⅱ类场地，当地的抗震设防烈度取7度，场地特征周期为0.35s，反应谱分析所需的其他有关参数：重要性修正系数为1.0，场地系数为1.0，阻尼比为0.02，水平向设计基本地震动加速度峰值为0.15g。由此可得到该地区标准设计反应谱曲线，如图4所示。

经过计算，选取主要截面进行结果分析，表3列出了三向正交分量独立作用下主梁跨中、1/4跨、塔顶、塔底的三向位移峰值，并按式(1)将三向正交分量进行组合。

图4 加速度反应谱

表3 三向正交分量独立作用下关键截面峰值位移(单位：mm)

由以上计算结果可知，各主要截面的纵向位移和竖向位移在三个方向的地震作用下均较小，跨中位置处最大竖向位移值仅为173.3mm，1/4跨位置最大竖向位移值为116.2mm；而横向位移在顺桥向和竖向地震作用下也很小，最大值仅为24.5mm，特别是在竖向地震作用下，截面的横向位移几乎可以忽略不计，而在横向地震作用下，截面出现较大的横向位移，最大值出现在主梁跨中处，其值为745.2mm。

当按式(1)进行地震作用组合时，即在三向地震力作用下，截面最大位移为跨中处的横向位移，为745.6mm，1/4跨横向位移值也较大，为530.2mm，塔顶的位移反应不显著，最大值为56.4mm。主梁跨中位置处在三向地震作用下最大竖向位移为176.9mm，最大纵向位移为155.9mm。

由于大跨径悬索桥第一阶阵型为主梁一阶对称侧弯，故其在地震作用下横向位移响应明显，越靠近跨中处，位移响应越大，且横向地震作用为最不利作用。

纵向输入时，悬索桥主要表现为主梁和主塔的纵向和竖向振动，横向振动效应很小，纵向振动与横向振动基本不耦合。

综上，在纵向地震作用下，主梁、桥塔主要表现为纵向振动，几乎没有横向振动效应；在横向地震作用下，主梁、桥塔主要表现为横向振动，桥塔除横向振动外还产生纵向振动，这主要是由主梁横向变形所控制；在竖向地震作用下，主梁主要表现为竖向振动，而桥塔主要表现为纵向振动，这主要由主梁竖向变形所控制。

5.2 动力时程分析结果

在地震时程分析计算过程中，分别考虑3种工况进行计算，其模式与前文反应谱分析相同，同时梁、墩截面的编号方式也与反应谱分析时相同。三向正交分量独立作用下关键截面峰值位移值见表4。

顺桥向地震波作用下，各最大截面位移时程分析结果，如图5所示。

横桥向地震波作用下，各关键截面位移时程分析结果，如图6所示。

竖向地震波作用下，各关键截面位移时程分析结果，如图7所示。

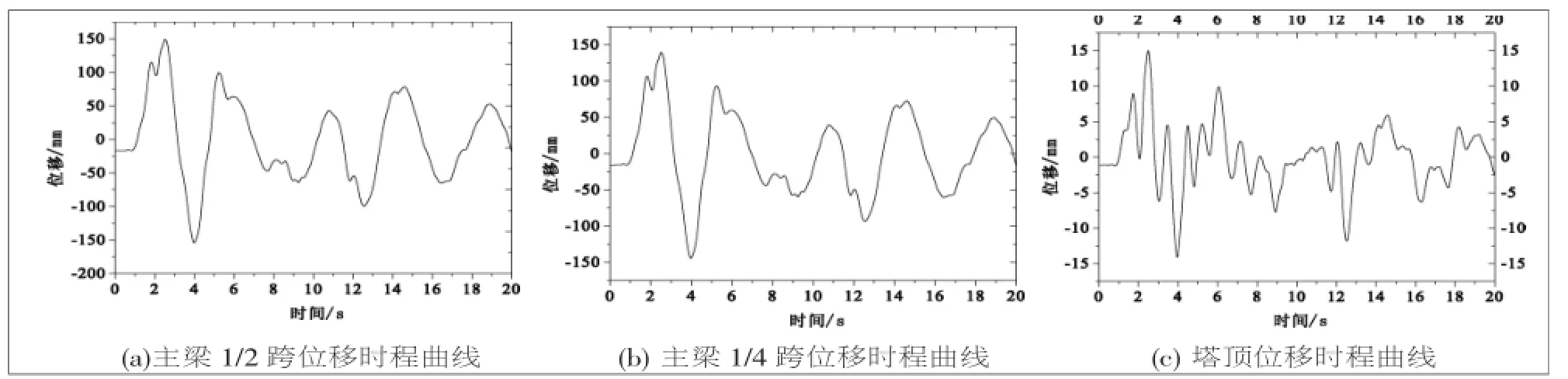
图5 顺桥向地震波作用下位移时程曲线

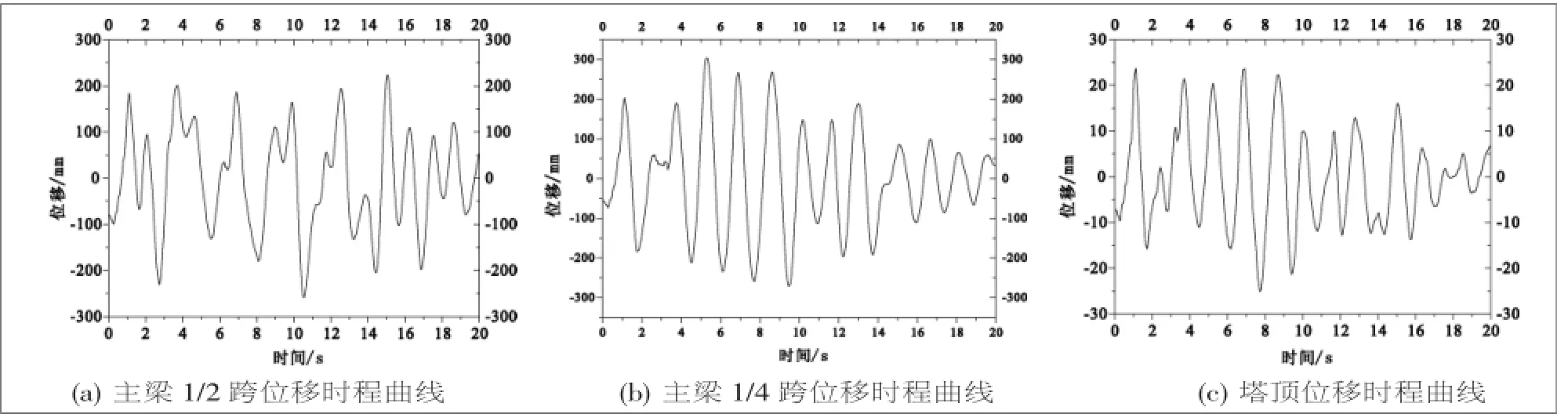
图6 横桥向地震波作用下位移时程曲线

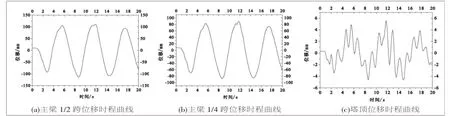
图7 竖桥向地震波作用下位移时程曲线

表4 三向正交分量独立作用下关键截面峰值位移(mm)

由表4可知，各主要截面在顺桥向和竖向地震作用下，横向位移均较小，最大峰值位移出现在主梁跨中处，位移仅为53.25mm，而在横向地震作用下主梁跨中横向位移峰值达到503.44mm，塔顶位移也达到79.09mm。顺桥向地震作用下，主梁的纵向位移最大值在主梁跨中位置处，峰值为149.29mm，竖向位移最大值在主梁1/4跨位置处，峰值为150.03mm；竖向地震作用下，各关键截面的纵向和横向位移值均较小，而对于竖向位移，主梁跨中截面位置处位移峰值达到290.24mm，主梁1/4跨截面处位移峰值达到202.43mm，塔底位移峰值达到147.88mm。在三向地震组合作用下，主梁最大位移峰值均出现在主梁跨中截面处，而主梁1/4跨截面位置位移峰值也较大，同样需要重点关注。

综上所示，在纵向地震波作用下，悬索桥主要表现为纵向振动，在横向地震波作用下，悬索桥表现为横向振动，而在竖向地震波作用下，主要表现为悬索桥的竖向振动，纵向、横向效应很小。

6 反应谱法与时程分析法对比分析

反应谱分析法与时程分析法都是两种重要的地震分析法。两种分析方法有着很大的区别，时程分析法考虑的非线性的问题，本文中主要考虑了结构非线性的问题，时程分析法不仅能得到地震反应的极值，而且更能得到该值随着时间变化的地震反应值[10]，对于反应谱法只能得到反应极值。

为分析、验证悬索桥在地震作用下的安全性，并对比反应谱分析和时程响应分析的可靠性，下面我们根据悬索桥地震反应谱分析和时程响应分析的计算结果，以主梁、桥塔位移为对比参数，进行两种方法的计算结果对比，数据如表5～表8所示。

表5 反应谱法与时程分析法位移计算比较(顺桥向地震力)

表6 反应谱法与时程分析法位移计算比较(横桥向地震力)

表7 反应谱法与时程分析法位移计算比较(竖桥向地震力)

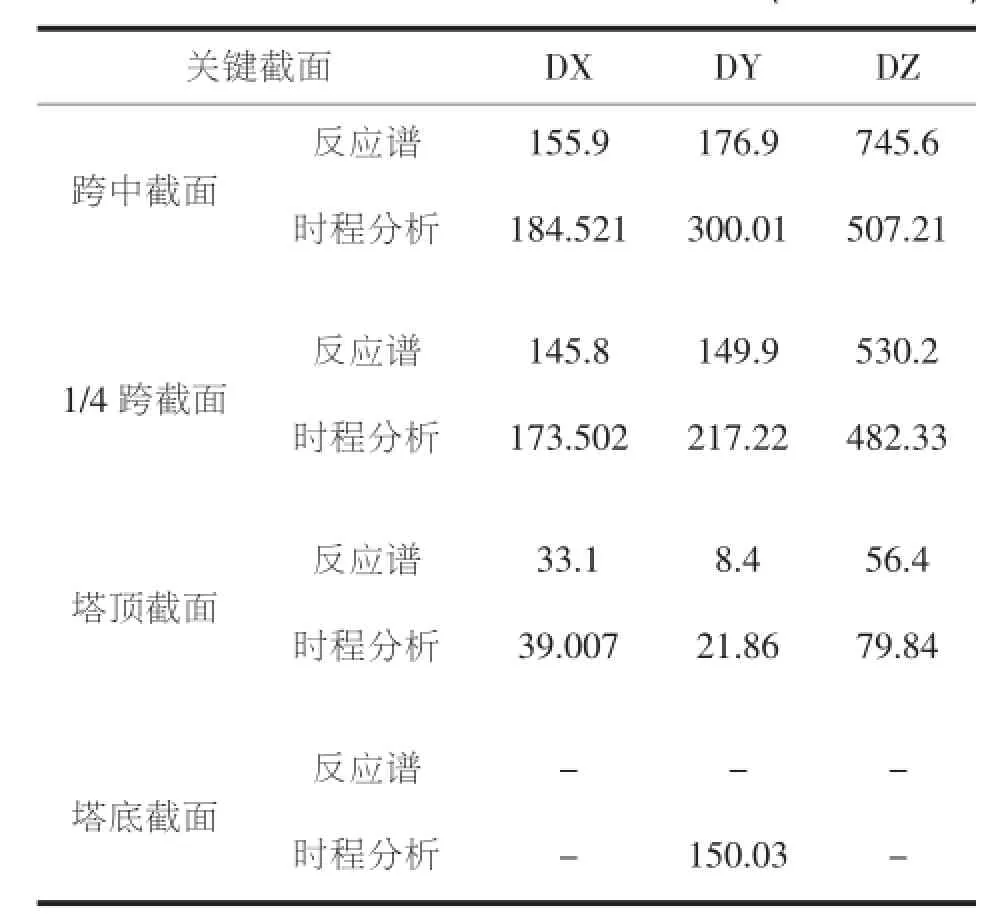
表8 反应谱法与时程分析法位移计算比较(组合地震力)

从反应谱和动力时程分析结果比较可发现，按反应谱计算得到的结果与按时程分析计算得到的结果变化不呈现规律性，但总体上来说，反应谱分析结果和时程分析结果相差不大。同时，在顺桥向和竖桥向的时程分析结果略大于反应谱；对于横桥向位移，反应谱分析结果大于时程分析结果，但是满足时程分析结果不小于反应谱法分析结果的80%。根据欧洲桥梁抗震设计规范(ENV 1998-2)第4.2.4条规定，时程分析法的结果不能用于放松根据反应谱法得到的结果。意思就是说如果时程分析法的结果比反应谱的结果小，就应该取反应谱法的计算结果。

因此，在运用已有的地震波记录进行大跨度桥梁的地震反应计算时，为安全起见，应该同时采用时程分析法和反应谱法进行计算，并取两者的较大值作为最后采用的结果。

由表8可以得到该悬索桥跨中截面处的横向位移最大值为745.6mm，因此应对悬索桥的侧向刚度加倍注意和重视。

不难发现，反应谱分析和时程分析在某些结构的响应上差距很大，根据规范反应谱分析主要适合中短桥梁，自振周期在6s以内的，而该悬索桥自振周期为6.24s，这可能是导致差距的一个原因，另一个原因可能是由于在动力时程分析的时候选择的非线性分析所致。