高中解析几何教学策略反思
2017-01-05江苏省南通市启东市吕四中学施红娟
江苏省南通市启东市吕四中学 施红娟
高中解析几何教学策略反思
江苏省南通市启东市吕四中学 施红娟
解析几何将数学方程用曲线直观地展示出来,降低了学生学习方程时的难度。同时,解析几何将“代数与几何”、“数与形”等连接了起来,更好地展现了数学中两大要素代数与图形之间的联系,是高中数学教学中不可缺少的一部分。学生在学习解析几何时,能够认识很多数学模型,也能够培养自己的空间想象力。近几年来,解析几何成为了高考的热点,新课程也对学生解析几何的学习提出了新的要求。因此,教师要认识到解析几何在高中数学教学中的重要性并采取有效的方法进行解析几何的教学。本文针对高中解析几何给出一些教学策略。
一、提高课堂讲课技巧
在解析几何的学习过程中,学生需要记忆并熟练掌握很多图形及公式。学生在学习过程中容易把知识点混淆,不能正确解答题目,因而会产生烦躁的情绪,甚至会对解析几何的学习失去兴趣,放弃学习解析几何。但是,如果学生对学习解析几何有很大的兴趣,那么他们一定会迎难而上,想办法解决学习中遇到的难题,这样学生学习解析几何就会越来越得心应手。学生不仅会学好解析几何,也有更大的信心取得一个优秀的高考成绩。更重要的是,这样会给他们一种解决难题之后的成就感,促进学生的身心健康发展。因此,教师要认识到提高课堂讲课技巧、调动学生的积极性、营造活跃的课堂气氛、吸引学生学习解析几何的兴趣的重要性。同时,教师也要采取一些有效的方式,达到吸引学生学习解析几何、并树立学习解析几何信心的目的。例如:在学习根据坐标求轨迹方程时,教师将求解步骤分为三步。此时,教师可以用篮球中的三步上篮来类比,将学生对篮球的兴趣引导到对解析几何的兴趣中去。这样既活跃了课堂气氛,吸引了学生的学习兴趣,也让学生对根据坐标求解轨迹方程的解题步骤有了深刻的记忆。
二、注重应用数学思想
在高中数学教学过程中,教师要让学生有一种应用数学思想解题的意识,有理有据。这不仅是在让学生规范解题思路和解题步骤,同时,也是在培养他们的逻辑思维能力,让学生学会理性的、有依据的解决问题,这对学生的其他科目的学习也是有好处的。高中数学思想有很多,如:分类讨论、转化法、类比法、运动变化与对立统一等。首先,分类讨论法主要应用在题目的解答有多种情况出现时。 例如,已知直角坐标平面上Q(0,2)和圆O:x2+y2=1,动点M到圆O的切线长与|MQ|的比等于常数a(a>0),求点M的轨迹方程,并说明它表示什么曲线。
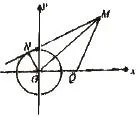
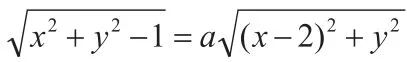
整理得:(a2-1)(x2+y2)-4a2x+(1+4a2)=0。
检验:坐标适合这个方程的点都属于集合P,故这个方程为所求的轨迹方程,于是:(1)当a=1时,方程化为x=5/4,它表示一条直线,该直线与x轴垂直且交x轴于点;(2)当a≠1时,方程化为,它表示圆,该圆的圆心坐标为(2a2/(a2-1),0),半径为。
本题在求出轨迹方程后,因参数a的值不同会导致曲线形状不同,因此要对a的取值进行分析,应用分类讨论法。其他各种数学思想也都有各自适用的题型。在解答解析几何题目时,学生形成应用数学思想解题的意识,不仅能够化繁为简,让他们有清晰的解题思路,而且,能够让学生发现问题中的特殊性,应用正确的解题方法,提高高中数学教师的教学质量。同时,教师要注意将各种数学思想交叉运用,让学生对这些数学思想有更熟练的应用。
三、传授多种学习方法
学生在学习解析几何的过程中,会遇到的题目有很多,学生不可能做完所有的题目。因此,教师在教学过程中,不能仅仅针对某一道题给学生进行讲解,重要的是学习方法的传授,应在讲解过程中,告诉学生这属于哪一类问题,这类问题的特点是什么,在解答这类问题时要注意的问题,以及解题的思路,让学生能够独立解决解析几何题,培养学生在学习中的独立能力。对于解析几何这种需要数形结合的思考量和计算量都比较大的题型,尤其需要学生有正确的学习方法和独立思考的能力。教师要让学生经常归纳总结解析几何的题型,并时常复习巩固。


本题看似新颖,分点数量也比较多,容易让学生产生慌乱的情绪,其实,学生只要能认真读题,仔细分析,不难看出本题是在考察椭圆的性质和距离公式。当学生了解了题目的题型及考查点,再运用所学的解决这类题的方法来进行解题时,就不会有畏难情绪,也能够对这类题型及运用到的知识点和解题方法有更深刻的记忆、更熟练的应用。因此,教师要认识到学习方法的传授对于学生学习解析几何的重要性,并尽可能地教授学生更多的学习方法。
总之,解析几何在高中数学中占有很重要的地位,也是高考的必考题型之一。因此,教师要认识到解析几何的学习对学生的重要性,并采取提高课堂授课技巧,吸引学生的学习兴趣,注重应用数学思想,及传授给学生多种学习方法等策略,提高学生学习解析几何的能力,进而提升教学质量。同时,在解析几何的学习中,需要学生有很好的空间想象力和逻辑思维能力等,因此,教师要注重培养学生的综合能力,促进学生的全面发展。
