锤片式饲料粉碎机内自由流的流场特性分析

2017-01-05孔丽丽边炳传彭观明庄宿涛许振保

饲料工业 2017年21期

■宋涛孔丽丽边炳传彭观明庄宿涛许振保

（1.泰山学院机械与建筑工程学院，山东泰安 271000；2.滕州市中等职业教育中心学校，山东枣庄 277500）

饲料加工业是发展农牧业的支柱产业，是联系种植业、养殖业和农副产品加工业的综合性产业[1-3]。新世纪以来，众多学者一直致力于对饲料加工设备的研究，在创新设备、改进结构、改善关键零部件性能、提高生产率、降低粉碎能耗等方面均取得了丰硕成果[1-7]。

饲料粉碎机是饲料加工的主要设备，按结构可分为锤片式、劲锤式、对辊式和齿爪式[4-6]。目前，我国使用较多的中小型饲料粉碎机是锤片式饲料粉碎机。在锤片式饲料粉碎机内部，受锤片高速旋转的影响，筛网附近会形成气流与饲料掺杂在一起的环流层，该环流层的存在意义颇受争议，学者们对此也作了大量研究。以环流层为界，可将粉碎机内气流分为加速流和自由流。外界气流与饲料原料相互掺杂，从喂料口进入粉碎机，受高速旋转的锤片影响，形成加速流，加速流从环流层破围而出，自由下行，称之自由流。自由流实质为高速的湍动气流，它不仅对饲料颗粒产生曳力作用，影响饲料的粉碎、破围和收集，而且对粉碎机能耗大、饲料过粉碎、饲料温升高、锤片磨损严重等问题也有较大的影响。从现有文献看，针对锤片式饲料粉碎机内自由流的流场特性的研究鲜有报道。

锤片式饲料粉碎机内自由流是包括三维有限流动、涡旋流动、脉动流动等多种流动因素共同形成的高速湍动气流，这使得粉碎机内自由流的流场呈现出相当复杂的分布状况，仅仅通过试验或解析等传统方法分析其特性，难度较大。本文采用数值模拟的方法，对粉碎机内自由流的速度场、压力场和湍动能场的分布特征和变化规律进行深入分析，并对自由流的流动状况作出较为准确的预报，以完善锤片式饲料粉碎机研究的基础理论。

1 研究模型

锤片式饲料粉碎机是将大尺寸的饲料原料粉碎至要求尺寸的机械设备，利用高速旋转的锤片反复击打饲料以实现干性饲料的一般性粉碎。考虑到从环流层破围而出的自由流不再受锤片和环流层的直接影响，而受粉碎机内部结构的影响，故而在分析自由流的流场特性时，可以忽略锤片和环流层的影响，将粉碎机内部结构简化为一个由入口、粉碎腔和出口构成的旋风式二维研究模型，如图1所示。

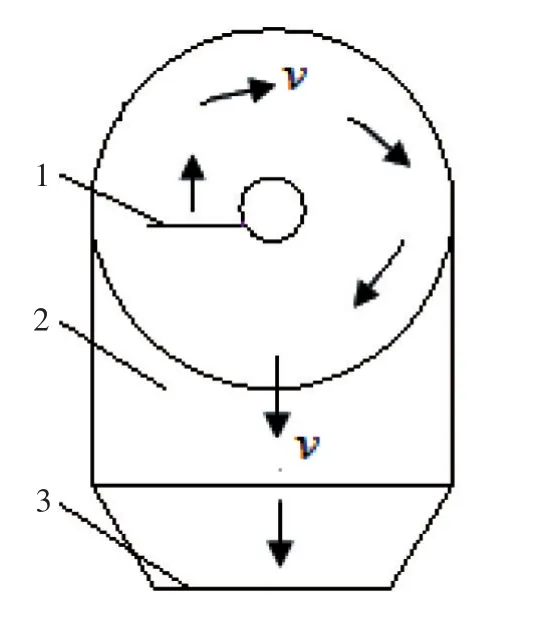
图1 研究模型

2 数值分析理论和方法

2.1 数值分析模型

锤片式饲料粉碎机内自由流虽然属于复杂的三维黏性非定常流动，但却遵守着质量守恒、动量守恒和能量守恒的三大基本定律，而且三大基本定律的连续方程、动量守恒方程和能量方程是流体运动分析的基本控制方程，也是数值分析技术的理论基础[8-9]。

在直角坐标系下，流体流动的数值分析模型可表示为：

连续方程：

动量守恒方程：

式中：p是流体的静压(Pa)；ρ是流体密度(kg/m3)；t是时间(s)；xi是坐标分量；ui是速度在某一方向上的分量；ρgi是i方向的重力体积力(N)；Fi是i方向的其他体积力（如源于两相之间的作用）(N)；τij是黏性应力张量，可以定义为：

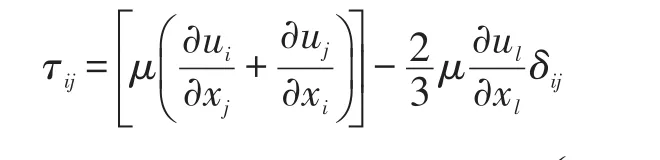
方程（1）和（2）称为雷诺平均的Navier-Stokes方程，与瞬时Navier-Stokes方程有相同的表达形式，只是速度或其他求解量变成了时间平均量。这两种方程既可以采用数学手段进行处理，或以笛卡尔坐标系表示，也可以求解不同类型的流体流动。

2.2 数值分析方法

研究湍流的方法主要有理论分析、数值模拟和试验研究，其中数值模拟和试验研究具有更重要的工程实践意义[10]。与试验研究相比，数值模拟方法更具有成本低、速度快等较显著的优点[11-12]。Gambit软件属于Fluent软件的前处理软件，主要用来几何建模和网格生成，把几何建模功能和网格生成技术很好地集成在一起，能够将相对复杂的几何区域划分出与相邻区域网格连续的、非结构化的混合网格。Fluent软件采用了多种求解方法和多重网格加速收敛技术，可以模拟从不可压缩到高度可压缩范围内的复杂流动，能够达到最佳的收敛速度和求解精度。

对于大多数湍流问题，其湍流流动的数值分析模型就是一组偏微分方程。为了便于计算机进行求解，需要先将这组偏微分方程转化为计算域中的每一节点上的一组代数方程，这就是所谓的网格生成。网格可分为结构网格和非结构网格两类。采用结构网格可以准确地处理边界条件，计算精度高，计算效率也较高，但对复杂外形的网格生成较难，甚至难以实现。采用非结构网格可以作网格的自适应处理，使得网格点足够密，提高计算效率和求解精度。

3 数值模拟与分析

3.1 计算模型设置

针对研究模型的二维结构，采用Quad网格（即网格形状呈四边形）和Pave（即网格排布方式呈平铺状）的网格生成方法。先将模型的入口网格数（Interval count）设置为50，再将几何面的网格大小（Interval size）设置为2，则共计生成网格数为30 166个。边界类型设置可以明确几何模型中那些代表模型边界的拓扑结构实体的物理特性和操作特性。由于研究模型的入口和出口均处于外界大气压，故可将入口边界设置为自由流速度入口类型（VELOCITY_INLET），出口边界设置为自由流出口边界类型（OUTFLOW），其余边界默认为WALL类型。

打开Fluent软件，导入研究模型，将模型尺寸的单位统一成毫米，数值计算模型采用RNG k-ε湍流模型，计算域的固体壁面采用无滑移边界条件（湍动能k=0，耗散率ε=0），近壁面区域流动则采用满足对数分布的标准壁面函数条件，其余设置如表1所示。设置完毕后赋初值（Intialize），进行迭代计算（Interval）。

表1 数值计算的相关设置

图2 数值计算残差图

从图2可以看出，在迭代计算的中后期，残差曲线存在小幅度的波动现象，这对计算结果影响不大。若要减小这种波动，可以适当调小数值计算的松弛因子（Solution Controls：Under-Relaxation Factors）。当残差曲线趋于某值而不再继续下行时，即便达不到设置的收敛精度0.000 1，也可认为本次计算是收敛的，这对数值计算结果的可靠性影响不大。

3.2 速度场分析

速度是一个矢量，是描述气流流动的最重要参数之一，也是表征气流能量的关键指标。

从图3可以看出，当入口气流的初始速度设置为20 m/s时，自由流呈现出如下3个特征：

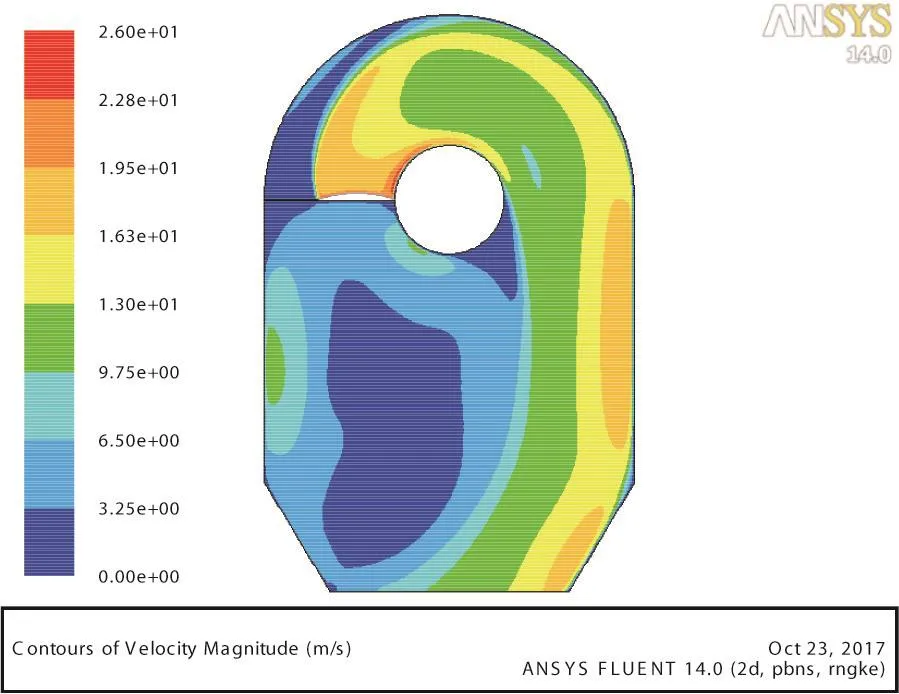
图3 粉碎腔内速度场云图

① 主流速度逐渐降至19.5、16.3 m/s和13.0 m/s，降速幅度分别为2.5%、18.5%和35%；粉碎腔壁面附近的气流速度保持在16.3 m/s左右，局部区域高达19.5 m/s，这说明从环流层破围而出的自由流多集中于粉碎腔内壁附近，并沿内壁面下行，直至从出口排出。

②自由流从粉碎腔内壁面由外向里逐渐降低，层次分明，呈现出向内壁面抛甩的趋势；受出口收缩结构的影响，自由流逐渐向出口中心线附近区域集中，这2个特征均有利于自由流的下行。

③ 在粉碎腔左侧空间内，气流速度保持在3.25 m/s左右，明显小于多数饲料颗粒的悬浮速度，这说明饲料颗粒在左侧腔体内滞留的可能性不大，有利于饲料颗粒的收集。

3.3 压力场分析

由于分子热运动才能决定物体的状态，而流体静压是分子热运动的反映。流体分子数越多，分子热运动的平均动能就越大，所以静压也就越大。因此，在分析流体的流动状态时通常用静压来表示。

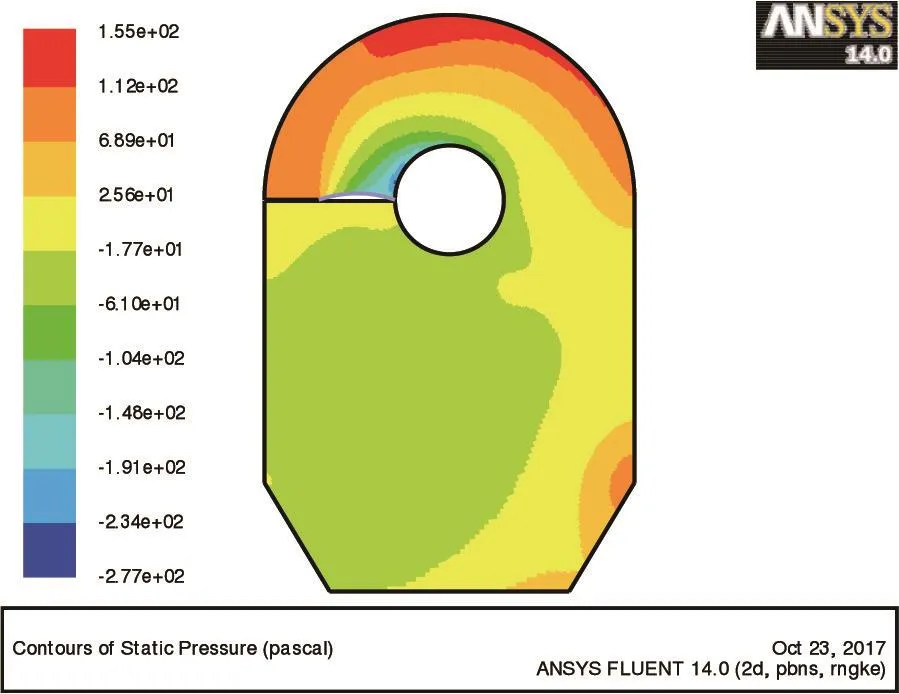
图4 粉碎腔内静压力场云图

从图4可以看出：

①在粉碎腔上部，出现大范围的高静压区，数值约155 Pa，主流静压则处于47.3～101 Pa。高静压区的存在会将自由流向下压制，产生回流，导致环流层附近气流出现大幅度降速趋势，既影响气流从环流层的破围，也不利于自由流的下行。

②在粉碎腔下部，出现了大范围数值约-6.76 Pa的负压区，这说明该区域气流分子较为活跃，可避免饲料颗粒的长时间滞留，有利于饲料颗粒的收集。

3.4 湍动能场分析

研究[13]认为，湍动能较大的地方湍动能耗散率也较大。湍动能耗散率是单位质量流体在单位时间内损耗的湍流动能的速率，也表征湍流强弱的重要参数。

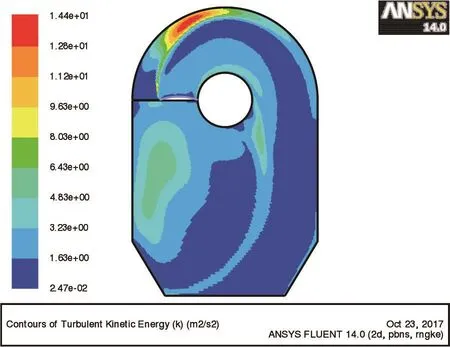
图5 粉碎腔内湍动能场云图

从图5可以看出，较大值的湍动能区域主要分布在粉碎腔上部，数值约14.4 m2/s2；左侧腔体区域，数值约5.4 m2/s2，说明这两个区域内包含了大量的湍动气流，流动极不稳定，较容易耗散能量。对比图3和图4发现，较大值的湍动能区域也是气流速度大幅度降低的主要区域。可见，较大值的湍动能场是导致气流速度大幅度降低的直接原因。