团簇CoFe2B2稳定性的密度泛涵理论研究

张成刚，方志刚，赵振宁，王茂鑫，刘继鹏，徐诗浩，韩建铭

(辽宁科技大学化学工程学院，辽宁鞍山114051)



团簇CoFe2B2稳定性的密度泛涵理论研究

张成刚，方志刚，赵振宁，王茂鑫，刘继鹏，徐诗浩，韩建铭

(辽宁科技大学化学工程学院，辽宁鞍山114051)

运用密度泛函理论(density functional theory, DFT)方法，在Becke3LYP/Lanl2dz水平下，对团簇CoFe2B2各个可能的构型进行优化，最终得到9种优化构型。本文从动力学、热力学稳定性2个方面对这9种构型之间的异构化反应进行分析，发现异构化反应的限度受团簇热力学稳定性的影响，提出一种线性方程lnK=0.391 9ΔE+0.435 7以预测团簇异构化反应的限度；多数构型通过一种或多种通道向构型2(2)转化；构型1(4)、2(4)两者之间的反应为可逆反应，构型1(2)无异构化反应发生并且具有很好的稳定性，最终存在构型为1(2)、2(2)、1(4)、2(4)，即戴“帽”三角锥和四角方锥两类构型。

团簇CoFe2B2；异构化反应；稳定性；密度泛函理论(DFT)

0 引言

自Eyring等人于20世纪30年代提出过渡态理论以解释化学反应机理与反应性的关系之后，依托过渡态理论，20世纪化学动力学，特别是生物酶的动力学研究得到了迅猛的发展[1-2]。在化学物理中，过渡态化学反应动力学的研究是非常重要的，但过渡态在反应过程中的存在时间非常短，无法测定其相关数据，故对其理论研究是非常有价值的。21世纪以来，过渡态理论研究和运用取得了长足的进展，如V.I. Anisimov等人巧妙地将过渡态理论与Wannier函数结合来分析无机物及单质的能隙差，取得了与实验数据吻合的结果[3]；日本研究者则通过过渡态探讨了化学反应的动态演变过程[4]。对过渡态化学动力学的研究也有了很大的突破，Unver等人发现了三原子分子的转动和振动与过渡态动力学之间的关系[5]，复旦大学LENG Jing等人提出了一种局部最优搜索测向算法LOR，使人们能更快地找到化学反应的过渡态[6]。目前发现的非晶态Co-Fe-B合金具有复杂的电子结构、空间结构，在电子[7-9]、电磁[10-20]、催化加氢[21]及新型电池[22-23]等领域具有很好的开发前景，根据过渡态理论研究其异构化反应的动力学和热力学确定其局域结构，可对非晶态合金相关性能的研究和新材料的制备提供有用的信息，但迄今为止鲜有这方面的报道。文献[24]在制备Co-Fe磁性纳米薄膜材料时使用Fe65Co35，本文根据其实验近似比例Fe∶Co为2∶1，组成团簇CoFe2B2，基于过渡态理论，从团簇动力学、热力学稳定性2个方面研究团簇CoFe2B2异构化反应，以确定其最终稳定存在的构型。

1 理论和方法

1.1 模型和优化计算

根据拓扑学原理，设计团簇CoFe2B2可能的空间结构，包括平面五边构型、三角双锥构型和四角锥构型。利用密度泛函理论(DFT)[25]，在Becke3LYP/Lanl2dz水平下，对这些可能的构型进行优化；然后运用QST2方法得到各优化构型之间异构化反应的过渡态空间结构。对Co、Fe原子采用Hay等人[26]的含相对论校正的有效核电势价电子从头算基组，即采用18-eECP的双ξ基组(3s，3p，3d/2s，2p，2d)，对类金属B采用Dunning/Huzinaga双ξ基组(9s，5p/3s，2p)。全部计算在启天M4390计算机上用Gaussian09程序[27]完成。

1.2 正、逆反应速率常数

用传统的过渡态理论(TST)的方法计算热化学动力学中各过渡态正、逆转化过程的速率常数，如式(1)：

k(T)=R(T)×kTST，

(1)

式(1)中R(T)用魏格纳校正系数求得：

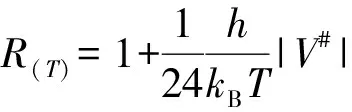
(2)

式(2)中V#指各过渡态中的虚频数(s-1)。

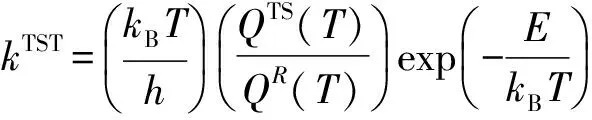
(3)

k(T)是过渡态反应过程中实际的速率常数，kTST为通过过渡态理论计算出来的速率常数，R(T)是真实反应速率常数与理论值之间的校正系数。另外，T是开尔文温度，kB为玻尔兹曼常数，h为普朗克常量，QTS(T)和QR(T)分别为过渡态和反应物的配分函数，E是转化过程中的活化能。

配分函数QTS(T)和QR(T)由公式(4)求得：

Qj(T)=Qtrans×Qrot×Qvib×Qelect，j=TS，R，

(4)

其中Qtrans、Qrot、Qvib、Qelect分别表示各构型平动、转动、振动和电子配分函数的组成成分。

2 结果与讨论

2.1 优化构型和过渡态构型的空间结构

图1为经过优化后的团簇CoFe2B2稳定构型，二、四重态构型各按能量由低到高排列(上标表示重度)；团簇CoFe2B2稳定构型中既有立体结构也有平面结构，立体结构包括戴帽三角锥和四角方锥结构。图2为这些优化构型之间异构化反应的5种过渡态构型(用TS表示)，并通过内禀反应坐标(IRC)验证及频率验证，各过渡态有且只有一个虚频，可以认为它们就是各异构体的过渡态构型；过渡态构型按能量由低到高排列如图2。综合来看，过渡态构型既存在立体结构，也存在平面结构：其中，平面构型参与的TS5(2)-2(2)为平面结构，且与平面构型5(2)结构相似；其他过渡态构型为立体结构。另外，不同重态之间不存在过渡态，TS2(4)-1(4)为四重态构型之间的转化，其他均为二重态之间的转化。除TS6(2)-4(2)外，其余转化均是向能量较小的构型2(2)、1(4)转化，互为对映异构体的3(2)、4(2)共同向2(2)转化时，过渡态结构相同，二者的成键、断键数目相同，均为1；能量较高的构型6(2)向4(2)转化时，过渡态构型能量最高(-1 158 266 kJ/mol)。此外，多数构型趋向于向构型2(2)转化。

2.2 异构化反应的化学动力学

2.2.1 异构化反应的能量参数和势能面

为从动力学稳定性角度分析团簇CoFe2B2异构化反应过程，表1和图3分别给出了各构型之间异构化的活化能(ETS指过渡态构型的能量，EaF、EaB分别指正、逆反应活化能)和势能面。

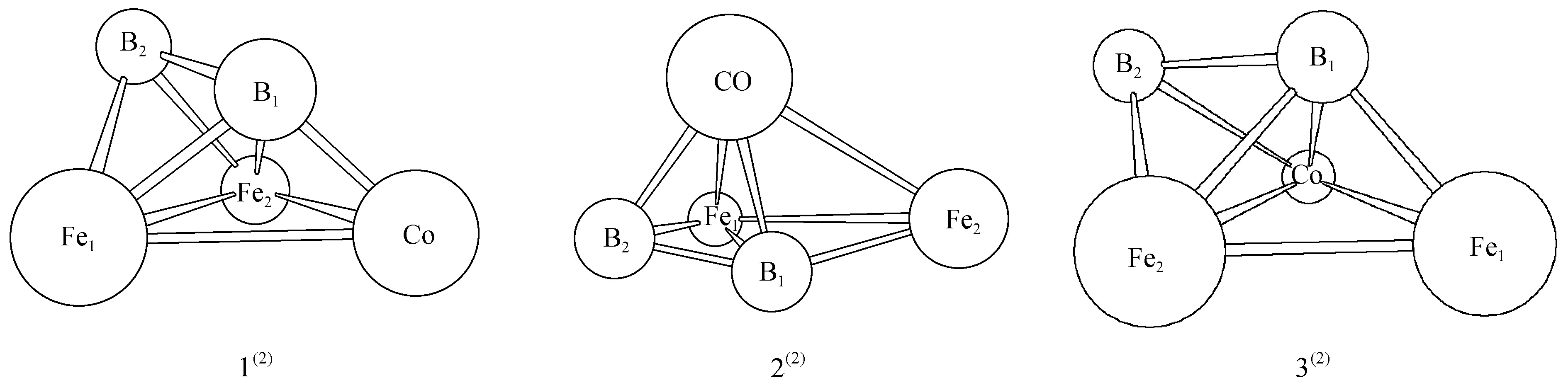
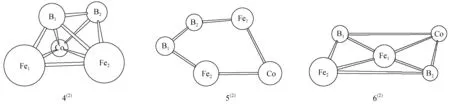
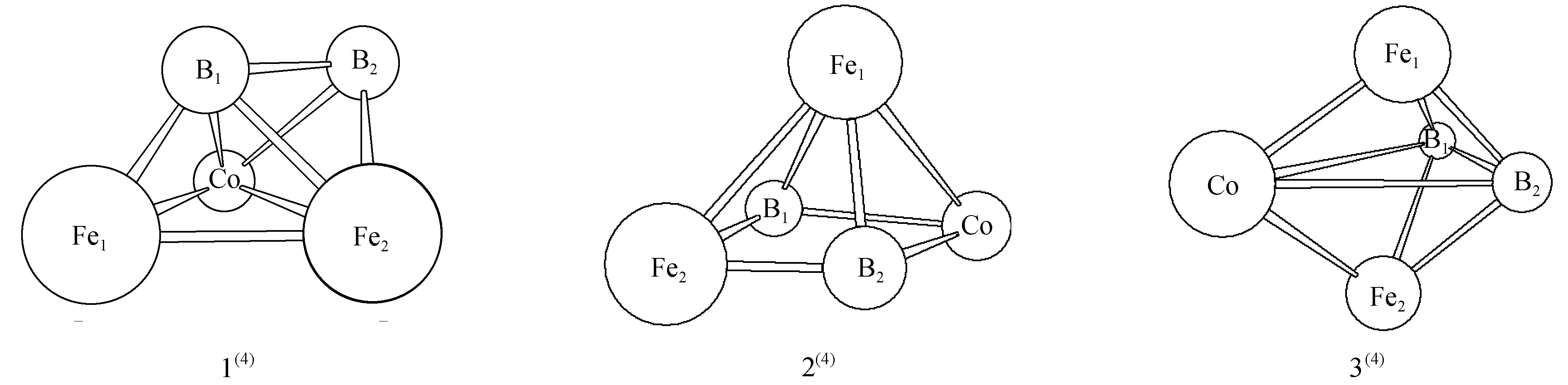
图1 团簇CoFe2B2的优化构型图Fig.1 Stable configurations of cluster CoFe2B2

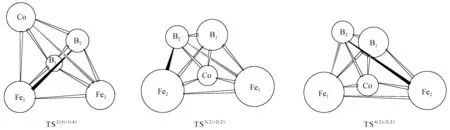
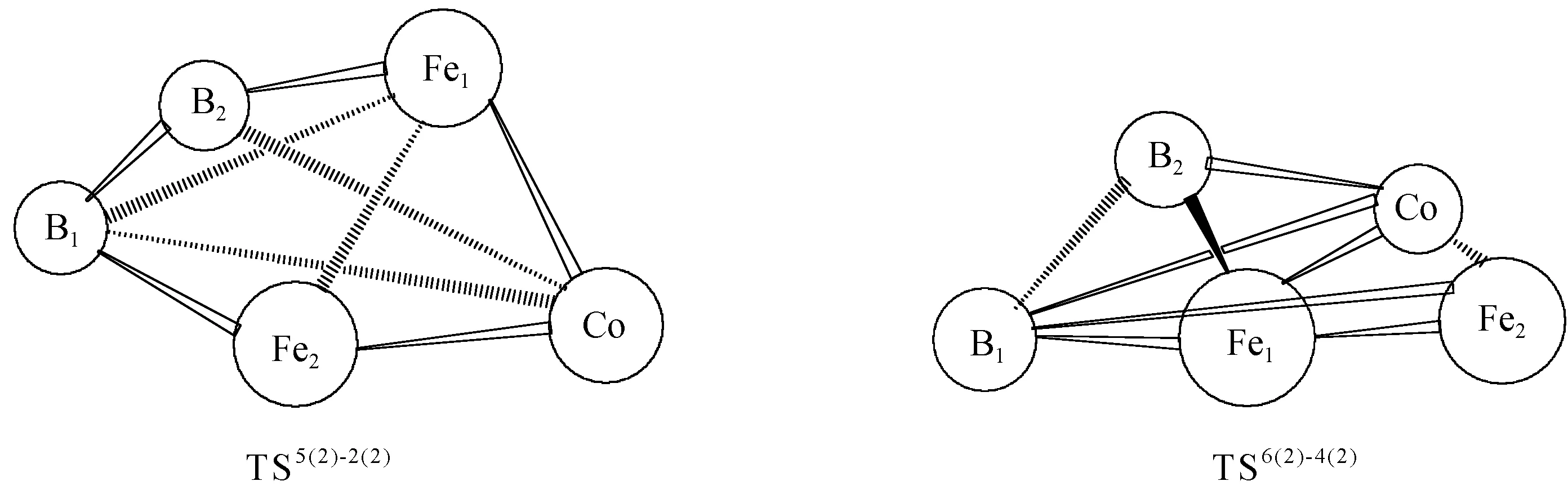
白实线表示转化过程中基本没有变化的键，黑实线表示转化过程中的断裂键，虚线表示转化过程中的生成键图2 团簇CoFe2B2各异构体转化的过渡态结构Fig.2 Transition structures of cluster CoFe2B2

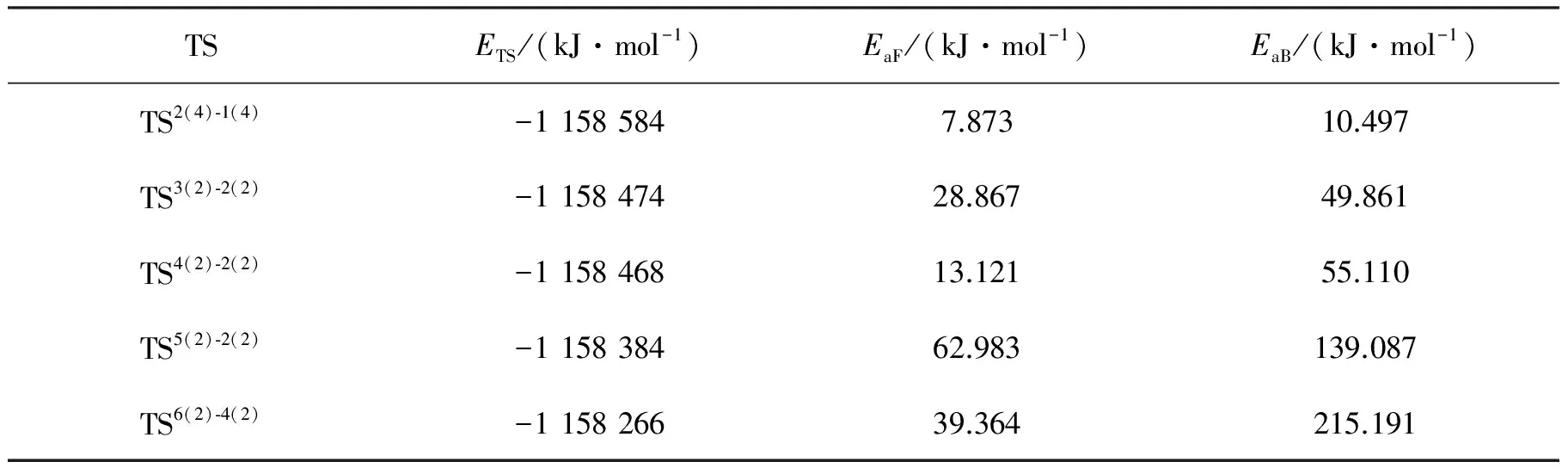
TSETS/(kJ·mol-1)EaF/(kJ·mol-1)EaB/(kJ·mol-1)TS2(4)⁃1(4)-11585847．87310．497TS3(2)⁃2(2)-115847428．86749．861TS4(2)⁃2(2)-115846813．12155．110TS5(2)⁃2(2)-115838462．983139．087TS6(2)⁃4(2)-115826639．364215．191

根据图3，构型1(4)、2(4)、2(2)在能势面上处于较低点，而由前面的讨论知，2(2)和1(4)是最可能的最终转化构型。各构型向2(2)转化存在3条通道：①6(2)→4(2)→2(2)，通过6(2)的Fe1—B2键的断裂转化为4(2)，再经过Fe2—B2键断裂转化为2(2)；②5(2)通过Fe1—B1、Co—B2、Fe1—Fe2键的生成转化为2(2)；③3(2)通过Fe2—B2键的断裂和Fe1—B2键的生成转化为2(2)。根据表1及图3可以发现这些反应的正反应活化能均小于逆反应活化能，说明反应容易进行，可见在热学条件下，构型2(2)落入相当深的阱深中，稳定性非常好。而向1(4)的转化只有通道2(4)→1(4)，此反应是通过Fe1—B2键的断裂和Fe2—Co键的生成完成转化，正反应活化能(7.873 kJ/mol)和逆反应活化能(10.497 kJ/mol)差别不大，故此反应是可逆反应。

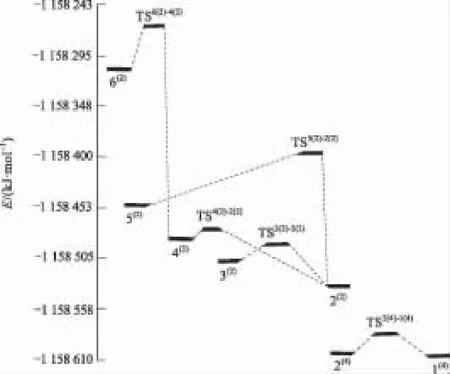
图3 团簇CoFe2B2的势能面Fig.3 Transition and potential energy surface of cluster CoFe2B2

从势能面上看，其他二重态构型通过一种或多种通道转化为稳定构型2(2)，构型2(2)落入相当深的阱深中，非常稳定；而构型1(4)、2(4)可相互转化、共存。

2.2.2 异构化反应的反应速率和平衡常数

为从化学动力学角度分析异构化反应，表2列出了各异构化反应的正反应速率k+、逆反应速率k-，反应平衡常数K由公式(5)求得：

K=k+/k-。

(5)

其中异构化反应6(2)→2(2)平衡常数由公式(6)求得：

K6(2)-2(2)=K6(2)-4(2)×K4(2)-2(2)。

(6)

表2 常温(298 K)下各异构转化过程的反应速率常数k和平衡常数K

综合来看，所有异构化反应的正反应速率均大于逆反应速率(K>1)。参考表1，正反应活化能均小于逆反应活化能，这符合阿伦尼乌斯公式：k=Ae-Ea/RT，慢的反应速率意味着大的活化能，说明所有反应均能向右进行，但不同的反应正、逆反应速率相对大小不同(K=7.28×10-1～2.153×1037)，可见各反应的反应限度是有所差别的，因此有必要探究反应物和产物热力学稳定性及其对反应限度的影响。

2.3 异构化反应的热力学

2.3.1 团簇各构型的热力学稳定性

为研究团簇热力学稳定性，表3列出了各反应物和产物及构型1(2)的能量，构型1(4)、1(2)、2(4)能量较低(分别为-1 079 866、-1 079 863、-1 079 863 kJ/mol)，且相差很小，可见这3种构型热力学稳定性最好。图4中，黑实线1、2中各点对应纵坐标分别表示对应构型的结合能Ebin和吉布斯自由能变Gg，二者由公式(7)、(8)求得：

Ebin=ECo+2EFe+2EB-ECoFe2B2，

(7)

Gg=GCoFe2B2-GCo-2GFe-2GB。

(8)

对应虚线分别指构型结合能和吉布斯自由能变的均值。图中明显看出，随着能量的增加，构型的结合能下降，吉布斯自由能变升高，且二者变化趋势相反；特别地，在所有团簇CoFe2B2构型中，只有1(4)、2(4)、1(2)、2(2)的结合能明显高于平均值，也只有这4种构型的吉布斯自由能变明显低于平均值，可见构型1(4)、2(4)、1(2)、2(2)最易生成，稳定性最好。

表3 团簇CoFe2B2各构型的能量Ecl

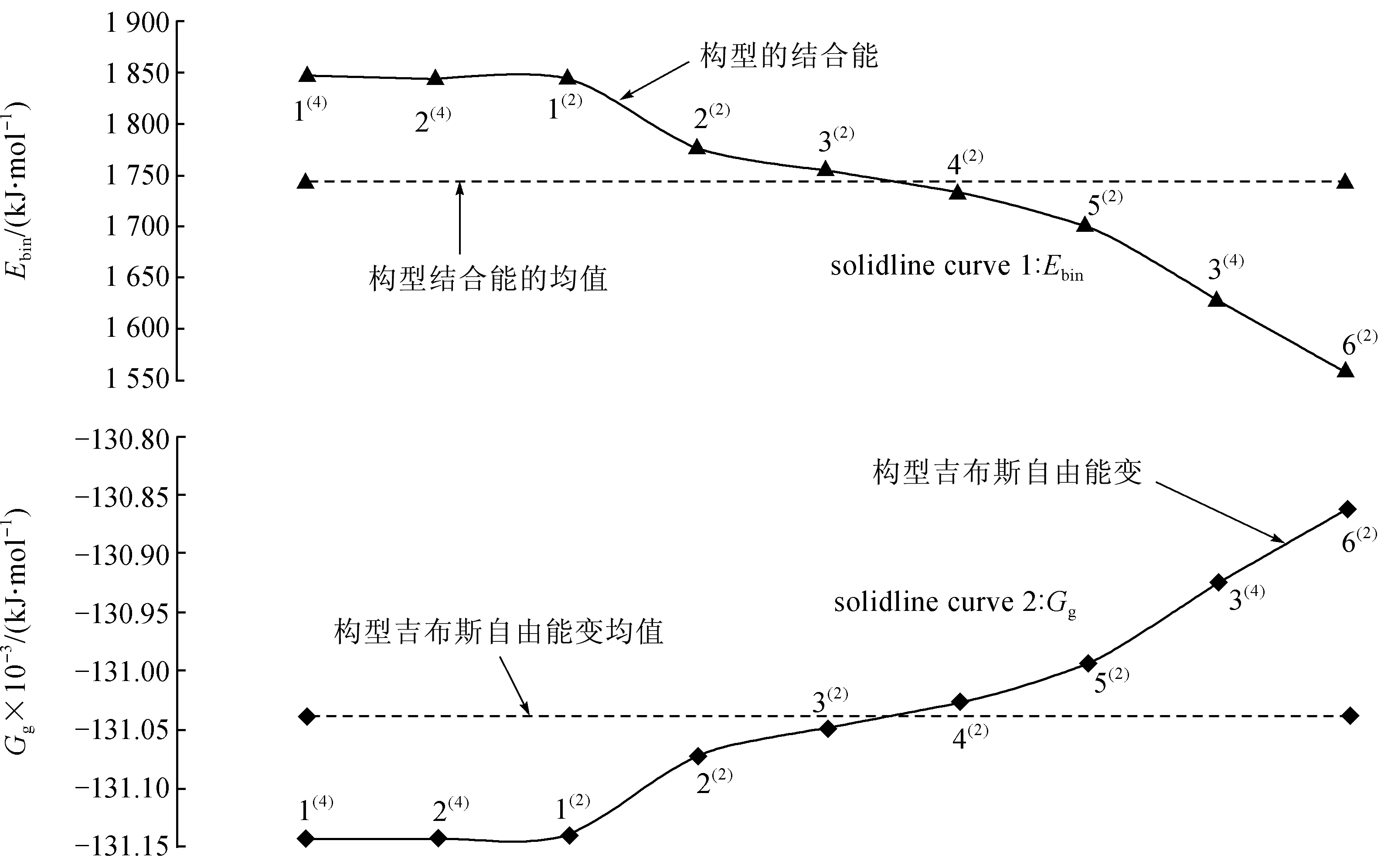
图4 团簇CoFe2B2各构型的结合能Ebin和吉布斯自由能变GgFig.4 The binding energy and change of Gibbs free energy of each configurations in cluster CoFe2B2

2.3.2 团簇热力学稳定性对异构化反应限度的影响

图5表示异构化反应中反应物与产物能量之差ΔE，其中反应2(4)→1(4)能量差最小(2.624 kJ/mol)；以构型2(2)为产物的反应中，反应物为3(2)、4(2)、5(2)、6(2)的反应能量差依次增高，显然，团簇CoFe2B2异构化反应的平衡常数随反应物和产物能量差的增大而增大，其中2(4)→1(4)的正、逆反应速率在所有反应中最大(4.962×1011、1.72×1011)，这可能是由于此反应中的过渡态构型能量低造成的(-1 158 584 kJ/mol)，但其K值最小(2.89)，说明此反应为可逆反应，构型1(4)、2(4)可共存；另外，向构型2(2)转化的反应3(2)→2(2)、4(2)→2(2)、5(2)→2(2)、6(2)→2(2)平衡常数依次增大(数量级分别为3、7、13、38)，这些反应均有较大的平衡常数，所以构型3(2)、4(2)、5(2)、6(2)与构型2(2)共存可能性非常小；特别地，能量差最大的反应6(2)→2(2)(75.827 kJ/mol)平衡常数最大(1.514×1038)，故此反应进行得非常彻底，构型6(2)几乎不存在。

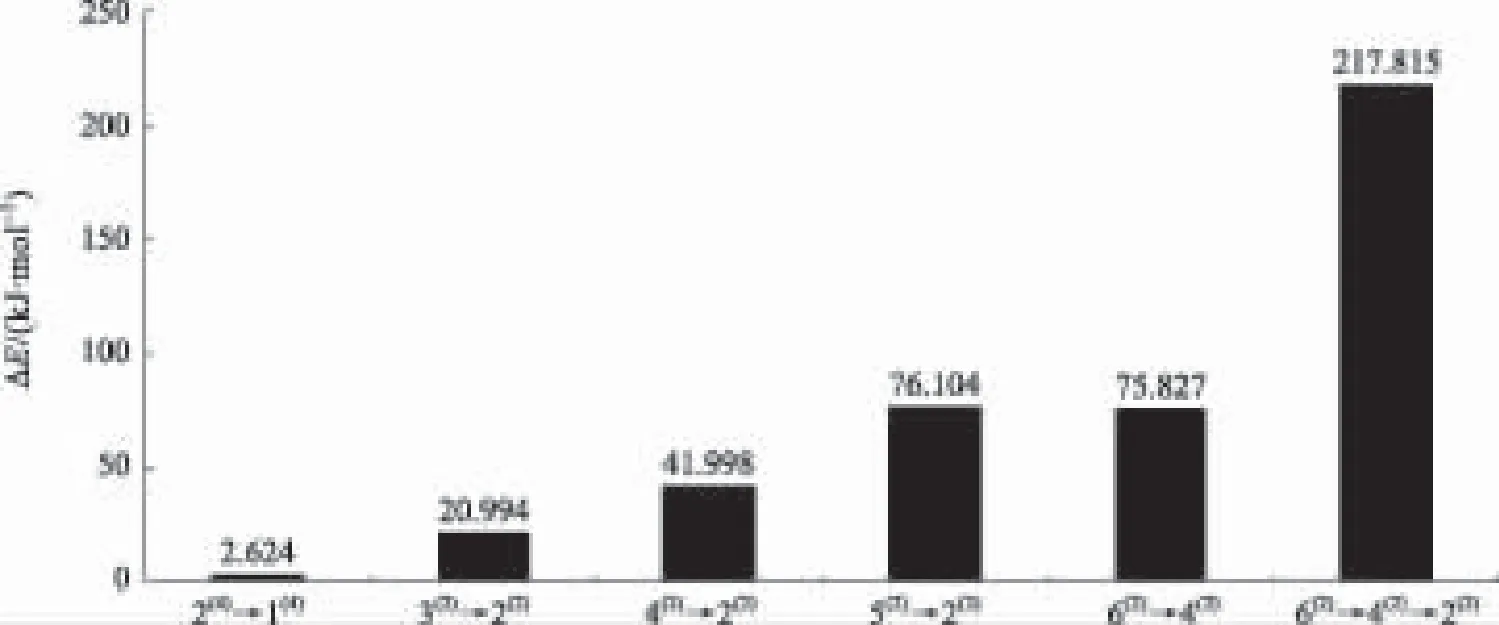
图5 不同反应中反应物与产物能量差值ΔEFig.5 The D-value(ΔE) of energy between reactants and resultants in different reactions

为进一步寻找团簇CoFe2B2热力学稳定性与异构化反应限度之间的关系，本文以反应物与产物能量差(ΔE)为横坐标、以反应平衡常数的对数lnK为纵坐标制得ΔE-lnK曲线如图6。从图6中明显看出ΔE-lnK曲线几乎为直线，故团簇CoFe2B2异构化反应的lnK与反应物和产物能量差为线性关系，直线方程为：lnK=0.391 9ΔE+0.435 7。本文根据此方程预测团簇其他异构化反应的反应限度，若反应3(4)→1(4)、3(4)→2(4)、2(2)→1(4)能够发生，则这3种反应的能量差ΔE分别为217.815、215.191、70.855 kJ/mol，将其代入方程lnK=0.391 9ΔE+0.435 7得到3种反应平衡常数分别为1.83×1037、6.7×1036、1.7×1012，可见若这些反应能够发生，则构型3(4)向1(4)、2(4)及2(2)向1(4)转化非常彻底。

化学热力学和动力学分析表明，构型1(4)、2(4)、1(2)热力学稳定性最好、最易生成；其他构型通过一种或多种通道转化为构型2(2)，反应2(4)→TS2(4)-1(4)→1(4)为可逆反应，异构化反应最终结果生成2(2)、1(4)、2(4)稳定的构型，1(2)无异构化反应发生，故团簇CoFe2B2最终稳定存在构型为热力学稳定性最好的1(2)、2(2)、1(4)、2(4)。转化过程可表示为图7。

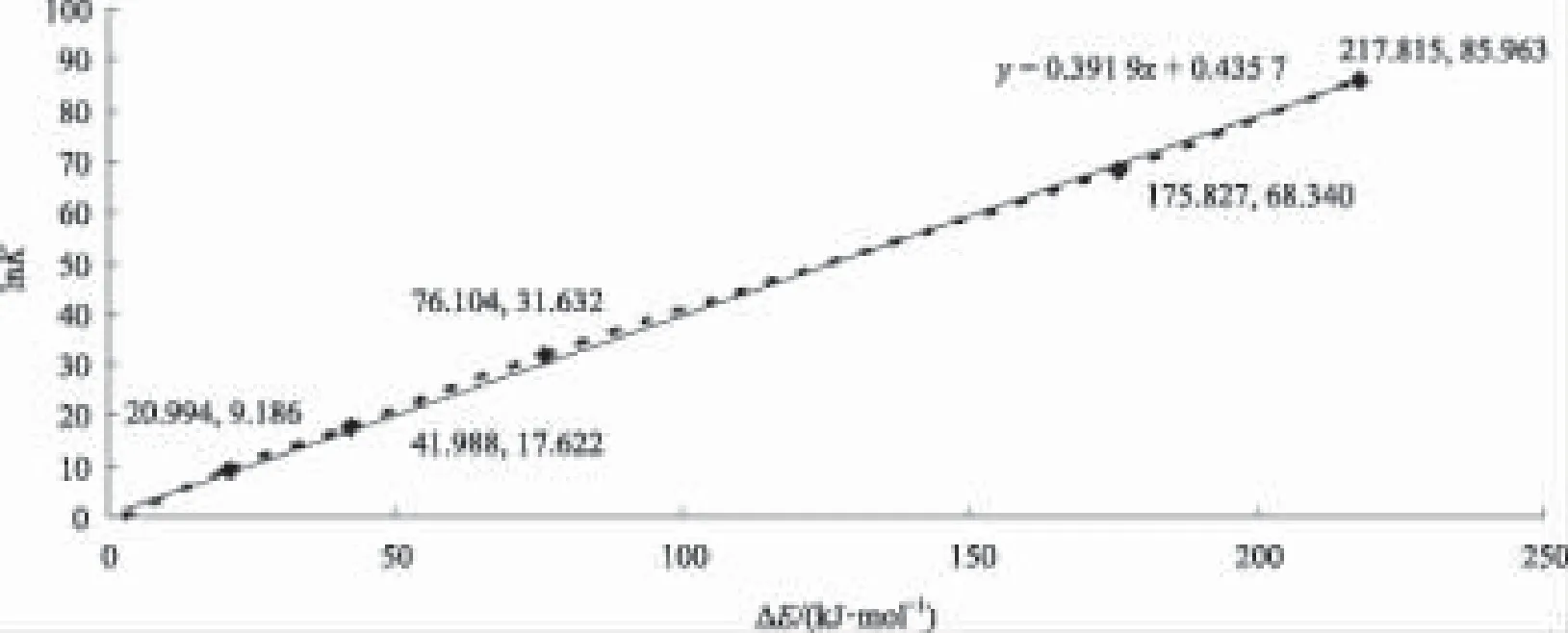
图6 反应平衡常数的对数lnK随反应物与产物能量之差ΔE的变化曲线Fig.6 The curve for order of magnitude of equilibriums constants changing with D-value of energy between reactant and resultant

图7 各构型之间的转化关系Fig.7 Transformation relation between different configurations

3 总结

本文从动力学、热力学稳定性2个角度对团簇CoFe2B2的异构化反应进行研究，结果表明反应限度受热力学稳定性的影响：反应物与产物能量相差越大，反应进行越彻底。故本文提出了一种线性方程：lnK=0.391 9ΔE+0.435 7，可根据反应物与生成物的能量差ΔE预测反应平衡常数K。团簇CoFe2B2中，构型1(2)不参与异构化反应，其他构型向稳定性较好的2(2)转化，1(4)与2(4)之间异构化反应为可逆反应，异构化反应最终结果生成可共存的构型2(2)、1(4)、2(4)，而构型1(2)、2(2)、1(4)、2(4)热力学稳定性最好，最容易生成，故团簇CoFe2B2最终存在的构型为戴“帽”三角锥和四角方锥两类构型。

[1] ALBERTY R A. The chemical kinetics of enzyme action[J]. Journal of American Chemical Society， 1958， 81(6)： 1521-1522.

[2] EYRING H. Transition states and enzyme kinetics[J]. BioScience， 1979， 29(8)： 485.

[3] ANISIMOV V I， KOZHEVNIKOV A V. Transition state method and wannier functions[J]. Physical Review B， 2005， 72(7)： 5125.

[4] LI C B， SHOJIGUCHI A， TODA M， et al. Dynamical hierarchy in transition states of reactions[J]. Few-Body Syst， 2006(2/4)： 173-179.

[5] ÇIFTÇI Ü， WAALKENS H. Reaction dynamics through kinetic transition states[J]. Physical Review Letters， 2013， 110(23)：182.

[6] GAO W， LENG J， SHANG C， et al. Efficient softest mode finding in transition states calculations[J]. Journal of Chemical Physics， 2013， 138(9)：094110.

[7] KALININ Y E， SITNIKOV A V， STOGNEI O V， et al. Electrical properties and giant magnetoresistance of the CoFeB-SiO2amorphous granular composites[J]. Materials Science and Engineering， 2001， 304： 941-945.

[8] STOGNEI O V， SLYUSAREV V A， KALININ Y E， et al. Hange of the electrical properties of granular CoFeB-SiOnnanocomposites after heat treatment[J]. Microelectronic Engineering， 2003， 69(24)： 476-479.

[9] SEEMANN K M， FREIMUTH F， ZHANG H， et al. Origin of the planar hall effect in nanocrystalline Co60Fe20B20[J]. Hysical Review Letters， 2011， 107： 312.

[10] WANG S L， HONG L L. Effect of the heat treatment on the structure and the properties of the electroless CoFeB alloy[J]. Journal of Alloys and Compounds， 2007， 429： 99-103.

[11] DADVAND N， JARJOURA G， KIPOUROS G J. Preparation and characterization of Co-Fe-B thin films produced by electroless deposition[J]. Journal of Materials Science： Mater Electron， 2008， 19(1)： 50-59.

[12] ZHANG S G， ZHU H X，TIAN J J， et al. Electromagnetic and microwave absorbing properties of FeCoB powder composites[J]. Rare Metals， 2013， 32： 402.

[13] ZHANG S， ZHAO Y G， XIAO X， et al. Giant electrical modulation of magnetization in Co40Fe40B20/Pb(Mg1/3Nb2/3)0.7Ti0.3O3(011) heterostructure[J]. Scientific Reports， 2014， 4： 3727.

[14] JEON M S， CHAE K S， LEED Y， et al. The dependency of tunnel magnetoresistance ratio on nanoscale thicknesses of Co2Fe6B2free and pinned layers for Co2Fe6B2/MgO-based perpendicular-magnetic-tunnel-junctions[J]. Nanoscale， 2015， 7： 8142.

[15] MOLINA C B， ZYSLER R D， ROMERO H. Anomalous magnetization enhancement and frustration in the internal magnetic order on (Fe0.69Co0.31)B0.4nanoparticles[J]. Applied Sciences， 2012， 2(4)： 315-326.

[16] HINDMARCH A T， KINANE C J， MACKENZIE M， et al. Interface induced uniaxial magnetic anisotropy in amorphous CoFeB films on AlGaAs(001)[J]. Physical Review Letters， 2008， 100(11)： 2339-2340.

[17] PALUSKER P V， LAVRIJSEN R， SICOT M， et al. Correlation between magnetism and spin-dependent transport in CoFeB alloys[J]. Physical Review Letters， 2009， 102(1)： 6602.

[18] IKEDA S， MIURA K， YAMAMOTOH， et al. A perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction[J]. Nature Materials， 2010， 9(9)： 721-724.

[19] HE W， ZHOU T， ZHANG X， et al. Ultrafast demagnetization enhancement in CoFeB/MgO/CoFeB magnetic tunneling junction driven by spin tunneling current[J]. Scientific Reports， 2013，3(10)： 1-5.

[20] TORREJON J， KIM J， SINHA J， et al. Interface control of the magnetic chirality in CoFeB/MgO heterostructures with heavy-metal underlayers[J]. Nature Communications， 2014，5：1-8.

[21] PEI Y， WANG J Q， FU Q， et al. A non-noble amorphous Co-Fe-B catalyst highly selective in liquid phase hydrogenation of crotonaldehyde to crotyl alcohol[J]. New Journal of Chemistry， 2005， 29(8)： 992-994.

[22] LIANG Y， WANG P， DAI H B， et al. Hydrogen bubbles dynamic template preparation of a porous Fe-Co-B/Ni foam catalyst for hydrogen generation from hydrolysis of alkaline sodium borohydride solution[J]. Journal of Alloys and Compounds， 2010， 491(1/2)： 359-365.

[23] WANG Y P， WANG Y J， REN Q L， et al. Ultrafine amorphous Co-Fe-B catalysts for the hydrolysis of NaBH4solutionto generate hydrogen for PEMFC[J]. Fuel Cells， 2010， 10(1)： 132-138.

[24] WANG G W， ZHANG F， ZUO H P， et al. Fabrication and magnetic properties of Fe65Co35-ZnO nano-granular films[J]. Nanoscale Research Letter， 2010， 5(7)： 1107-1110.

[25] BECK A. Density-functional thermochemistry. Ⅲ. The role of exact exchange[J]. Journal of Chemical Physics， 1993， 98(7)： 5648-5652.

[26] HAY P J， WADT W R. Abinitio effective core potentials for molecular calculations[J]. Journal of Chemical Physics， 1985， 82(1)： 270-283.

[27] FRISCH M J， TRUCKS G W， SCHLEGEL H B， et al. Gaussian 09， revision C.01[CP]. Wallingford C T： Gaussian， Inc.， 2010.

(责任编辑 王龙杰)

The Density Functional Theory Study on Stability of Cluster CoFe2B2

ZHANG Chenggang， FANG Zhigang， ZHAO Zhenning， WANG Maoxin， LIU Jipeng， XU Shihao， HAN Jianming

(School of Chemical Engineering， University of Science and Technology Liaoning， Anshan Liaoning 114051， China)

Nine stable configurations were gained after a series of cluster CoFe2B2models were optimized and calculated under the Becke3LYP/Lanl2dz level by using density functional theory (DFT) method. Isomerization reactions of those stable configurations were studied from thermodynamics and dynamics. A logarithmic equation is proposed to predict the limit of isomerization reaction， namely lnK=0.391 9ΔE+0.435 7； most of stable configurations were converted to configuration 2(2)through one or more doors and the isomerization reaction of configurations 1(4)/2(4)is reversible； there is no isomerization of configuration 1(2)taking place， and the final existence of cluster CoFe2B2are configurations 1(2)2(2)1(4)2(4)， namely capped triangular and quadrangular pyramid structures.

cluster CoFe2B2； isomerization reaction； stability； density functional theory(DFT)

10.16088/j.issn.1001-6600.2016.03.012

2016-01-24

国家自然科学基金资助项目(51144008)；国家级大学生创新创业训练项目(201510146039)；辽宁省大学生创新创业训练项目(201510146009)

方志刚(1964—)，男，辽宁鞍山人，辽宁科技大学教授，博士。E-mail：lnfzg@163.com

O64

A

1001-6600(2016)02-0086-09