三角形平面图的若干性质探讨

徐肇銮，郭秀山，杨文荣

（河北工业大学 电气工程学院，天津 300130）

三角形平面图的若干性质探讨

徐肇銮，郭秀山，杨文荣

（河北工业大学 电气工程学院，天津 300130）

首先叙述了三角形平面图G的顶点V、边E和面F的关系．因为G不会存在顶点数大于4的完备图的子图，所以如分成一个个由2个相邻三角形面构成的子图，对比2个三角形面而言，其公共边是唯一的．其次引入其对偶图的边与顶点的关系，并应用了置换群的概念，对顶点做换位运算，可以导出对顶点所连接的3条边可以分别属于3个不相交的集合．因此对偶于原三角形平面图的每个三角形面的3条边，也分别属于3个不相交的边的集合．最后可以得出这样的结论，只用4种颜色来对三角形平面图的顶点正确着色的充要条件是：三角形平面图中，不存在4个顶点以上的完备图的子图．

对偶图；完备图；结合矩阵；置换群；换位；四色定理

1 顶点、边和面的关系

图是包括许多个点和把这些点连接起来的线段，以及这些线段围成的区域的总称．这些点被称为图的顶点，顶点的集合用V表示．这些线段被称为图的边，边的集合用E表示．这些线段围成的区域，被称为面，它的集合用F表示．这点顶点和边可以画在1个平面上．除顶点之外，任何两边之间不许有交点，则称为平面图．因为现在要讨论的图，它的面都是由3条边围成，而且必须画在1个平面上，所以称为三角形平面图[1]．本文用G V,E表示，或简单用G表示．

由图中某一顶点出发，又回到这一顶点的边，称为自环．那么它只是一条边围成1个面．如果在2个顶点之间，有2条或2条以上的边，都接在这同2个顶点之间，这样2条边就围成1个面，称为多重边．现在我们要讨论的图G，每个面都要用3条边围成，所以没有自环和多重边．图G最外的边，也应只有3条边．在这3条边之外，直至无限的区域，也构成了1个面，被称为无界面，在讨论平面图时，必须包括它们在内[2]．现在要讨论的图G，只有1个连通片在每一条边上，也没有指出方向，所以是简单无向图．

如图G的顶点数用v表示，边数用e表示，面数用f表示，连通片为l，那么根据著名的欧拉公式

由此得到

每个顶点所连接的边数，称为该顶点的结合度或简称度，用d vi表示．

因为每条边都要有2个顶点连接，而一共有e=3v 6条边．所以把所有每个顶点的结合度加起来的总和，应该是2e=6v 12，因此它的平均值.

从上式可以看出，在G中总有某些顶点的结合度比6小，即某些顶点的结合度

如果1个图Gi的顶点的集合和边的集合是原图G的子集合，那么Gi为原G的1个子图．在三角形平面图中，不会出现有4个以上顶点的完备图的子图，只能出现只有4个顶点的完备图，即可以有4个顶点的度都为3的完备图的子图[3]．

例1任意给出1个图G，如图1所示，它的v=8， e=3v 6=18，f=2v 4=12，顶点1，6，8，5及 e8，e16，e6，e7，e13，e15构成的1个子图是1个v=4的完备图．所有相邻的2个三角形面结成一对，都可以形成1个子图，例如f1与f2结成1个子图，也可以f1与 f3，或 f1与 f12形成1个子图．这样的子图应包括4个顶点，5条边，2个三角形面，中间一条边为此2个三角形面的公共边．2个相邻三角形面，有且仅有此1条公共边[4]．如图2所示．

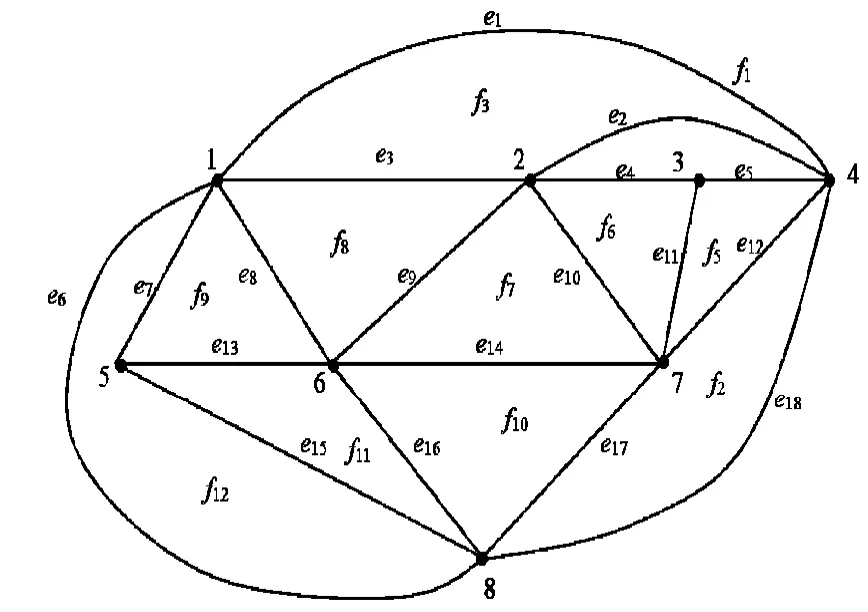
图1 三角形平面图Fig.1 Triangular plan graph

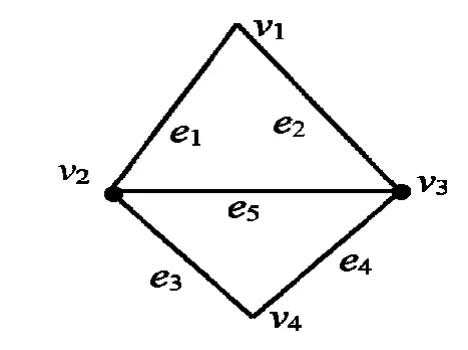
图2 由2个三角形面结对的子图Fig.2 Pair consists of two triangular faces subgraph

2 对偶图

因为凡是平面图都可以有其对应的对偶图．三角形平面图也应有其对偶图，简单地说：原图G的边与其对偶图的边一一对应；原图G的顶点与其对偶图的面一一对应；原图G的面与其对偶图的顶点一一对应．

可以在原图G每个三角形面中画置1个顶点，一共应有2v 4个顶点，把这些顶点用边都一一连接起来，就构成了原图G的相应的对偶图，用GD表示[5]．图3画出图1中G的对偶图．从图可以看出对偶图的边都一一跨接或者说一一切割原图G的边，所以二者的边数相等，而且对偶图顶点的结合度都等于3．顶点数等于原图G的面数f，对偶图的面数等于原图G的顶点数v．

把对偶图GD的顶点用1，2，……，2n 4表示，然后列出1个2n 4×2n 4的正方形表格．如某2个顶点有边连接，那么在表格中，相应的行和列用1表示，否则为0，称为GD的顶点结合矩阵．图3中GD的顶点结合矩阵如图4所示．

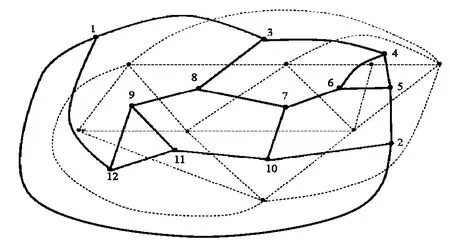
图3 图1三角形平面图的对偶图（实线所示）Fig.3 The dual graph of triangular planar graph in Fig.1

图4 GD顶点结合矩阵Fiq.4 Vertex binding matrix of graph

从上面的矩阵中可以看出，这2v 4=12个对偶图的顶点，都与这2v 4=12个顶点的全体中，相邻3个顶点有边连接．因为共有2v 4个顶点，所以这些连接的边一共必须有条，分别连接这2v 4个顶点，相应连接的顶点至少有3种不同，即这2v 4个顶点至少有3种不同的排列．

根据置换群的概念，n个元素应有n!个排列．那么上述的3种排列一定包含在这n!个排列之中，而且仅是一种两两换位，有许多零元素，所以计算不是很大．从上面的例题可以看出，结合矩阵的对角线上是零元素，对角线上下的非零元素是对称的，所以在写出第1行的行编号和列编号后，从第2行起，要先写出对角线以下的非零元素的行和列编号，它应该在上面出现过，但行和列的编号互相换位，然后再写出这一行中对应于结合矩阵对角线上面出现的非零元素所应有的行和列的编号．如此等等，把所有一对对的行和列的编号所代表的非零元素排成3排，手算即已完成．图GD的3个不同的排列如表1所示[6]．

相应也求得了3种连接在所有2v 4个顶点之间的边．

这n=2v 4个顶点 (它一定是偶数)，每个顶点都要“发出”3条边，与其相邻的3个顶点有3条边各自连接．根据狄里克莱抽屉原则，这n个顶点中也一定是每个顶点都有3条来自不同的3个顶点的3条边“到达”．“发出”和“到达”是可以视为一样的，所以这共有的条边一定可以分3类，分别为条边，一类为蓝色（b），一类为绿色（g），一类为红色（r），而且是不相交的．

然后，利用置换群中换位的概念，依据结合矩阵中顶点与顶点的结合关系，对顶点的排列进行置换，即可以把所有条边分出不同颜色的3类．每个顶点一定“发出”3条不同颜色的边，每个顶点也一定有3条不同颜色的边“到达”．任一类颜色的边一定不会有2条或者2条以上连接起来．任一条边不同具有2类或2类以上的颜色．

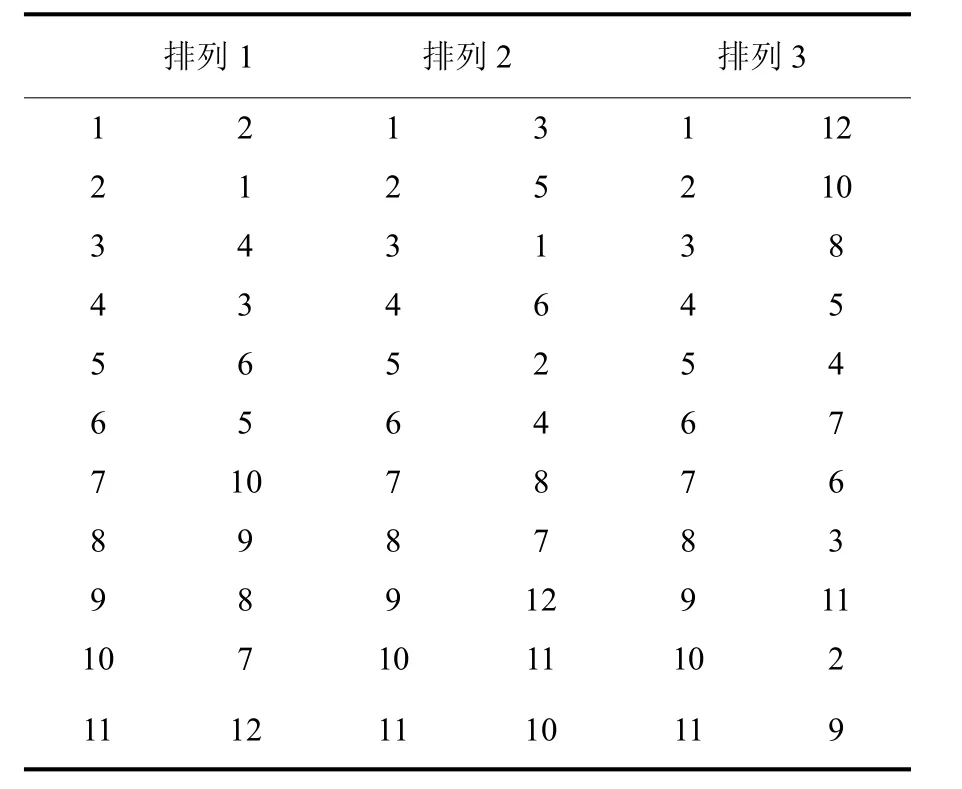
表1 图GD的3个不同排列Tab.1 Three arrangements of gragh GD

3 图G的3个不相交边集

三角形平面图G的边数e=3v 6，等于其对偶图GD的边数．因为GD中的每个顶点都置于原三角形平面图G的每个三角形面之中．由这一顶点“发出”或“到达”的3条边，都与该三角形面相邻的3个三角形面中的对偶图的顶点相连接．它们都具有b、g、r 3类不同颜色，而且所有这3条对偶图的边都“跨过”或者说都“切割”原图G中该三角形面的3条边，被哪一种颜色的对偶图边“切割”，那么就对应地也着该类颜色．因此图G的每个三角形面的3条边也都各具有3类不同颜色，因此G的所有3v 6条边可分成3个不相交的边集：Eb、Eg、Er．那么．

因此，G的每个三角形面的3条边都必须是各有且仅有此b、g、r3类颜色．

4 图G顶点的着色

所谓正确着色，就是要使图G中每条边的两端顶点具有2种不同的颜色．因此是必须使每个三角形面的3个顶点具有3种不同颜色．

如果取A、B、C、D 4种颜色中的3种来对三角形面的3个顶点着色，那么就有种取法，分别是ABC，ABD，CDA，CDB 4种．

如果把三角形面的3条边分别着以b(蓝)，g(绿)，r(红)3类颜色．若边的颜色为r，则其两端顶点颜色为A、B或C、D．若边的颜色为g，则其两端顶点着以A、C或B、D．若边的颜色为b，则其两端顶点着以B、C或A、D．

按照上述规定之后，那么三角形面的3条边都是b、g、r 3种颜色的情况下，每个三角形面的3个顶点的颜色就一定可以是上述4种取法的一种．反过来说，如果三角形面的顶点颜色为上述4种取法的任一种，那么这三角形面的3条边都是具有b、g、r3种颜色，所以二者是等价的．

图G中任何1个三角形面都可以做到用b、g、r3类颜色来对3条边着色，因此每个三角形面的3个顶点也一定可以用4种取法的任一种来着色．

四色定理：三角形平面图的顶点可以只用4种颜色来正确着色的充分必要条件是三角形平面图中不可能有4个顶点以上的完备图的子图[7]．

证明：因为三角形平面图可以分为v 2个2个相邻三角形面结合在一起的子图Gi，如图2所示，无论这一顶点在原图G中，它的结合度有多大，它在上述的子图Gi中的结合度只能是3或2，而且任意1个三角形面可以与其相邻的3个三角形面分别结合成3个不同的子图Gi，于是每个三角形面的3条边，都可以是这三个不同的子图Gi的3条公共边．做到这一要求的必要条件，就是因为G中没有4个顶点以上的完备图的子图．如果有4个顶点以上的完备图存在的话，那么可能G中有一条边不是唯一的，而是2个三角形面的公共边，有可能是3个三角形面的公共边．每个三角形面中所置的顶点发出的边，可能有4条，不是均为3条．而原图G的边，不是一一被切割，有可能被切割2次，即不能一一对应，不可能构成3个不相交的边的集合．所以图G中没有4个顶点以上完备图的子图是必要条件．反过来说，图G中不存在4个顶点以上的完备图的子图，那么无论是原图G或者其对偶图，它们的边数相等，而且一一对应，都可以构成3个不相交的边的集合．原图G的所有三角形面的3条边，都分属于这3个不相交的边的集合，用不到其他条件．所以图G中不存在4个顶点以上的完备图的子图也是充分条件．证毕．

5 结束语

四色问题是1852年英国F.Guthrie提出的，直到1976年，美国K.oppel，W.Hahen，J.Koch宣布他们借助计算机，证明了四色问题，但有的学者持不同看法．本文提出，利用对偶图中顶点与边的关系，根据狄里克莱抽屉原则，就可以说明对偶图的边完全可以分成3个不相交的集合，再根据置换群中的一种换位置换，得到3个顶点的3个不同的排列，即可求出，对偶图的边的3个不相交集合．因它与原图的边一一对应，所以也得到了3个不相交的边的3个集合，这里完全不需要计算机的帮助．

我们知道1个图（包括非平面图）的顶点的正确着色数，可以是10顶点中最大结合度．而对偶图顶点结合度均为3，所以对偶图的顶点是可以只用4种颜色来正确着色．但由此我们绝不可以认为三角形平面图的顶点（或由此即可导出）也只需4种颜色来正确着色．因为原图与对偶图，是面与顶点，或顶点与面一一对应．顶点与顶点，面与面不能一一对应．只有边与边是一一对应．本文就是利用边与边的对应关系，来导出边可以只用3种颜色，才导出其顶点可以用4种颜色来正确着色．

[1]龚光鲁．有限数学引论 [M]．上海：上海科学技术出版社，1981．

[2]陈树柏．网络图论及其应用 [M]．北京：科学出版社，1982．

[3]卢开澄．组合数学算法和分析 [M]．北京：清华大学出版社，1983．

[4]祁忠斌，叶东，张和平．3-正则图的环边连通性和环连通性之间的关系 [J]．山东大学学报（理学版），2009，44（12）：22-24．

[5]王艳丽，苗连英．图的集合边色数 [J]．山东大学学报（理学版），2012，47（6）：67-70．

[6]Oleg V Borodin，Anna O Ivanova．Precise upper bound for the strong edge chromatic number of sparse planar graphs[J]．Discussiones Mathematicae Graph Theory，2013，4（4）：759-770．

[7]谢力同．极大平面图的组合运算 [J]．系统科学与数学，1993，13（4）：323-330．

[责任编辑 代俊秋 夏红梅]

Several property of triangular planar graph

XU Zhaoluan，GUO Xiushan，YANG Wenrong

(School of Electrical Engineering,Hebei University of Technology,Tianjin 300130，China)

In this paper,firstly,the relationship of edges,vertexes and faces of Triangular Planar Graph G is explained. Because G does not have a complete subgraph with vertex number more than 4,it is divided into several subgraphs Gi, which are composed of two adjacent triangles.The every common edge of two triangles is unique.Secondly,relationship between edges and vertices of the dual graph of G is proposed.And the concept of permutation group is applied to do commuting operations on vertexes of dual graph.It can be deduced that the three edges which are connected by a vertex can be respectively belong to three disjoint sets.Therefore,the three edges of each triangle of the dual graph are respectively belong to the set of three disjoint edges.At last,the conclusion is obtained.The necessary and sufficient condition for the correct coloring with only four colors to vertexes of the triangular planar graph is that there is no complete subgraph with 4 vertices or more in the triangular planar graph.

dual graph;complete graph;adjacency matrix;permutation group;commutation;Four Color Theorem

O157.0

A

1007-2373(2016)05-0023-05

10.14081/j.cnki.hgdxb.2016.05.004

2016-09-06

徐肇銮（1928-），男（汉族），副教授．