基于CWLS的多运动站TDOA/GROA辐射源定位算法

孙 顺，董 凯，修建娟，刘 瑜

(海军航空工程学院 信息融合研究所，烟台 264001)

工程与应用 doi:10.3969/j.issn.1673-5692.2016.05.015

基于CWLS的多运动站TDOA/GROA辐射源定位算法

孙 顺，董 凯，修建娟，刘 瑜

(海军航空工程学院 信息融合研究所，烟台 264001)

针对多运动站的到达时间差(TDOA)和到达增益比(GROA)的辐射源定位问题，提出了一种无源定位算法。传统定位模型需要利用中间变量构造线性方程,不适用于多运动站连续定位。针对该问题，本文推导了无需中间变量的TDOA/GROA联合定位模型，然后根据量测模型推导了误差项，并推广到所有历史量测，提出了基于约束加权最小二乘(CWLS)的多运动站辐射源定位算法，最终通过对加权矩阵和约束矩阵进行广义特征值分解得到目标的状态估计。所提算法避免引入中间变量带来冗余的问题，无需初始化过程,性能更加稳健。仿真结果表明该算法性能逼近克拉美罗下界(CRLB)且是渐进无偏的。

辐射源定位；约束加权最小二乘；时差；增益比；中间变量

0 引 言

随着信息技术的快速发展，无源定位技术已经成为信号处理领域的重要研究课题，并广泛应用于雷达[1]、声呐[2]、无线通信[3]、无线传感器网络[4]等领域。时差(TDOA)定位体制是多站无源定位中最常见的体制，具有稳定、高精度等优点。目前的时差定位算法中，多通过引入额外的中间变量(辐射源到参考观测站的径向距离)建立线性时差方程。在此定位模型基础上，文献[5]给出了经典的两步加权最小二乘(TS-WLS)算法，文献[6]则给出了对其改进后的BiasSub法和BiasRed法；文献[7]提出了总体最小二乘(TLS)算法，改善了定位精度；通过考虑中间变量和辐射源之间的约束关系，文献[8]提出了二次约束的最小二乘算法，但是计算量太大，文献[9]提出了约束总体最小二乘(CTLS)算法，文献[10]提出了约束加权最小二乘(CWLS)算法，进一步提高了定位精度。另一方面，由于辐射源信号会随着传播而产生能量衰减，Ho等人尝试将达到增益比(GROA)加入到TDOA体制中，利用GROA量测对中间变量的修正，改善对辐射源的定位精度[11]，文献[12]对文献[11]的方法进行了改进。文献[13]和文献[14]提出了联合TDOA/GROA信息的CTLS方法和CWLS方法，进一步提高了定位精度。以上都是使用的基于中间变量的定位模型的定位算法，对于多运动站的情况下，由于观测站不断运动，中间变量即辐射源到参考观测站的径向距离也在不断变化，使得上述定位模型及其算法无法直接推广到多运动站连续定位，需要建立新的定位模型。

文献[15]研究了时差瞬时定位方程，通过对双曲线方程进行转化，得到了只与目标状态向量有关的线性方程，从而避免了引入中间变量。文献[16]基于此模型推导了TDOA连续定位算法，在此基础上，本文推导了GROA定位模型，并提出了一种基于CWLS的TDOA/GROA联合定位算法，并对其性能进行了理论分析与仿真验证。

1 无需中间变量的TDOA/GROA联合定位模型

1.1 TDOA定位模型描述

(i=1,2,…,M-2)

(1)

采用文献[16]的方法对式(1)做变换，可得无测量误差时的TDOA线性方程为

(2)

式中：

其中，c为光速。

图1 典型定位场景示意图

实际到达距离差(RDOA)测量值中含有测量噪声

(3)

(4)

(5)

式中：T为观测时间，ω为信号带宽，ρ=Psignal/Pnoise为信号的信噪比，Psignal和Pnoise分别为信号和噪声的功率谱密度函数，IM-1为M-1阶单位矩阵，1(M-1)×(M-1)为M-1阶全1矩阵。

原有需要中间变量的TDOA定位模型通过两步最小二乘的方法，需要先得到目标状态和中间变量的联合估计值，然后利用约束条件对待求的目标状态进一步求精。由式(1)和式(2)可知该TDOA定位模型不需要估计中间变量，减少了待估计参数数量，简化了算法流程，达到去冗余的目的，也没有增加其他观测量，适用于多运动站的无源定位。

1.2 TDOA/GROA联合定位模型推导

为推导无需中间变量的TDOA/GROA联合定位模型，首先推导基于GROA的定位模型。

根据信号传播理论，不考虑多径效应时，信号的传播损耗与信号源和传感器之间距离的n次方成正比，在自由空间中，可将损耗因子n设定为常数2[17]，则

(6)

(i=2,3,…,M)

(7)

(i=3,4,…,M)

(8)

这样我们就得到了无测量误差时的GROA线性方程

(9)

式中：

实际到达增益比测量值中含有测量噪声

(10)

(11)

(12)

原有需要中间变量的GROA定位模型通过联合TDOA和GROA量测方程得到ri1=(gi1-1)D1，可知原模型通过加入GROA量测信息提高对中间变量D1的估计精度，进而提高算法性能，并没有通过GROA量测直接改善目标定位精度。由式(8)和式(9)可知所提无需中间变量的GROA定位模型能够直接估计目标状态，并避免引入中间变量，适用于多运动站的无源定位。

综上所述，通过引入GROA定位模型，构建TDOA/GROA联合定位模型，可以充分利用GROA中包含的目标位置信息，提高算法性能，并且保持了无需中间变量的优点，适用于多运动站对固定目标的连续定位。其联合定位模型为

(13)

2 基于CWLS的无源定位算法

(14)

将式(15)带入式(13)，整理后可得

bk-Akx=Δbk-ΔAkx=Ckvk

(16)

定义加权矩阵

(17)

从而得到加权最小二乘(WLS)算法的最小化代价函数为

(18)

其定位解的解析表达式为

(19)

将WLS定位解推广到前k时刻的所有观测量，可得

(20)

(21)

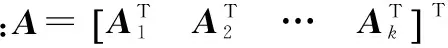
因为回归变量和回归从属变量之间的误差相关性[6]，所以WLS算法是有偏的，因此将其建模为CWLS模型[6][18]。

定义增广矩阵

Au=[-Ab]

(22)

和增广解向量

X=[x 1]T

(23)

易得

(24)

式中：

则式(20)可被重写为

(25)

带入式(24)并对ε求期望，可得平均代价函数为

(26)

正是第二项的存在，当最小化E(ε)时，使解偏离真值从而产生偏差。因此，当约束第二项为常数时，E(ε)将在X取得真值时达到最小值。于是可构造CWLS问题为

(27)

(28)

(29)

注意到随着时间的推进，矩阵维数快速增大，导致计算量剧增，可利用式(30)和式(31)避免高维矩阵直接相乘，从而减小计算量，也可以对该算法加窗处理[20]，提高算法的实时性。

(30)

(31)

3 性能仿真与分析

对2维空间而言，至少需要4个观测站才能得到闭式解，仿真中选用4个运动观测站采用TDOA/GROA联合定位体制对固定辐射源连续定位，观测站的初始状态如表1所示，固定辐射源位于(200 km,300 km)处。设采样点数为Tω/π=200 000，连续观测200个周期。考察第k周期辐射源状态估计的均方根误差(RMSE)为

(32)

表1 观测站的初始状态

(1)连续定位算法比较

图2 不同算法连续定位性能对比

从图2可以看出随时间的推移，三种算法的定位误差不断下降。其中RLS算法在第30周期后，开始快速偏离CRLB，这是因为该算法仅对各时刻的瞬时定位结果进行了平滑，并没有充分利用历史量测信息。本文所提的WLS算法和CWLS算法能够充分利用所有量测信息，使定位性能逼近CRLB，其中CWLS算法由于引入约束矩阵，使其优于WLS算法，定位精度更高，收敛速度更快。

(2)信噪比对定位性能的影响

设带宽因子c/ω为100 m，蒙特卡罗次数N=100，改变信噪比SNR，图3分别给出了RLS算法，WLS算法，CWLS算法与CRLB定位性能比较的曲线图。

图3 定位RMSE随SNR变化对比

由图3可知，随着SNR减小，以上三种算法的定位精度均有不同程度下降。其中RLS算法由于对历史量测利用有限，在整个SNR范围内都无法达到CRLB的估计精度，SNR小于-23 dB时，产生门限现象，大幅度偏离CRLB。WLS算法在高信噪比情况下能够逼近CRLB，但由于其算法是有偏的，随着量测噪声增加，SNR小于-10 dB时，开始缓慢偏离CRLB。本文所提的CWLS算法性能明显优于以上两种算法，能够达到CRLB的定位精度，直到SNR小于-23 dB时，算法性能才开始偏离CRLB。

(3)带宽因子对定位性能的影响

固定SNR为20 dB，其他仿真条件不变，以上算法性能随带宽因子的变化情况如图4所示。

图4 定位RMSE随c/ω变化对比

由图4可知，RLS算法的定位RMSE随着c/ω的增加而下降，并且在整个c/ω范围内比CRLB高5 dB 以上。当c/ω小于46 dB时，所提的WLS算法和CWLS算法都能达到与CRLB相同的定位精度，当c/ω大于46dB时，WLS算法开始偏离CRLB，但CWLS算法偏离较小，其定位RMSE优于WLS算法。

由于假设采样点数Tω/π不变，随着c/ω增大，采样间隔T增大，观测站运动路程也在增加。当c/ω增大到30 dB以后，飞机接近并飞过观测站1、2、3和目标共线的位置，由文献[22]可知，在该区域附近T型布置观测站对目标的观测精度有所改善，导致36 dB后的观测精度都有所提升，并随着c/ω增大逐渐降低。

设采样点数Tω/π=20 000，SNR为20 dB，其他条件不变，将TDOA/GROA联合定位性能与仅用TDOA量测的定位性能进行仿真比较，其结果如图5所示。

图5 不同定位体制对定位RMSE影响随c/ω变化对比

由图5可知，当c/ω较小(小于50 dB)时，TDOA/GROA联合定位体制与仅用TDOA的定位体制的定位性能基本一致，当c/ω较大(大于50 dB)时，TDOA/GROA联合定位体制的定位性能更加优秀；相同定位体制时，相对于WLS算法，CWLS算法性能更优。

通过观察式(4)和式(11)中TDOA和GROA的量测噪声协方差，并对其作商，可得

(33)

由上式可知，随着c/ω的增大，虽然TDOA和GROA的量测误差都在增大，但相对于TDOA量测信息，GROA量测拥有相对更高的量测精度，其对定位性能的贡献应当更大。这也就解释了当c/ω较大时，TDOA/GROA联合定位体制的优越性，表明所提GROA定位模型是有效的。

(4)CWLS算法偏差分析

令信噪比分别为-7 dB、-4 dB、0 dB，其他条件与1)小节一致，考察第k周期目标状态估计的偏差

(34)

仿真结果如图6所示。由图6可知，不同SNR条件下，随着观测时间的增加，本文CWLS算法的偏差趋于零，说明该算法是渐进无偏的。同时可知SNR越小，算法收敛越快。

图6 不同SNR下CWLS算法偏差

4 结 语

推导无需中间变量的TDOA/GROA联合定位模型，带入量测模型推导了误差项，并推广到所有历史量测，进而提出了CWLS连续定位算法，并给出了求解方法。所提算法充分利用历史量测数据，并且不需要初始化，适用于多运动站无源定位的情况。仿真结果表明该方法的定位精度逼近CRLB且是渐进无偏的。

[1] 杨建华.雷达无源定位技术的发展与战术应用[J].中国电子科学研究院学报, 2009, 4(6):601-605.

[2] FLUCKIGER M, NEILD A, NELSON B J.Optimazation of receiver arrangements for passive emitter localization methods[J].Ultrasonics, 2012, 52(3):447-455.

[3] RAPPAPORT T S, REED J H, and WOERNER B D.Position location using wireless communications on highways of the future[J].IEEE Communications Magazine, 1996, 34(10):33-41.

[4] GHOLAMI M, CAI N, BRENNAN R W.Evaluating alternative approaches to mobile object localization in wireless sensor networks with passive architecture[J].Computers in Industry, 2012, 63(9):941-947.

[5] CHAN Y T and Ho K C.A simple and efficient estimator for hyperbolic location[J].IEEE Transactions on Signal Processing, 1994, 42(8):1905-1915.

[6] HO K C.Bias reduction for an explicit solution of source localization using TDOA[J].IEEE Transactions on Signal Processing, 2012, 60(5):2101-2114.

[7] HUANG Z, LU J.Total least squares and equilibration algorithm for range difference location[J].Electronics letters, 2004, 40(5):323-325.

[8] YANG K, AN J P, XU Z.A quadratic constraint total least-squares algorithm for hyperbolic location[J].I.J.Communications, Network and System Sciences, 2008, 1(2):130-135.

[9] CHEUNG K W, So H C, Ma W K, et al.A constrained least squares approach to mobile positioning:algorithms and optimality[J].EURASIP Journal on Applied Signal Processing, 2006, 2006:1-23.

[10]LIN L X, So H C, CHAN F K W, et al.A new constrained weighted least squares algorithm for TDOA-based localization[J].Signal Processing, 2013, 93(11):2872-2878.

[11]HO K C, SUN M.Passive source localization using time differences of arrival and gain ratios of arrival[J].IEEE Transactions on Signal Processing, 2008, 56(2):464-477.

[12]郝本建, 李赞, 万鹏武, 等.基于TDOA与GROA的信号源被动定位偏差消除技术[J].电子学报, 2014, 42(3):477-484.

[13]刘艳芳, 杨育捷.基于约束总体最小二乘方法的联合TDOA/GROA信号源定位算法[J].电光与控制, 2015, 22(12):93-97.

[14]杜彦伸, 魏平, 张花国.一种新的基于TDOA与GROA的无源定位算法[J].航空学报, 2015, 36(9):3034-3040.

[15]BAKHOUM E G.Closed-form solution of hyperbolic geolocation equations[J].IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(4):1396-1403.

[16]徐征, 曲长文, 骆卉子.无需中间变量的多运动时差定位新算法[J].航空学报, 2014, 35(6):1665-1672.

[17]石明卫, 莎柯雪, 刘原华.无线通信原理与应用[M].北京:人民邮电出版社, 2014.37-53.

[18]HO K C, CHAN Y T.Geometric-polar tracking from bearings-only and Doppler-bearing measurements[J].IEEE Transactions on Signal Processing, 2008, 56(11):5540-5554.

[19]HO K C, CHAN Y T.An asymptotically unbiased estimator for bearings-only and Doppler-bearing target motion analysis[J].IEEE Transactions on Signal Processing, 2006, 54(3):809-822.

[20]关欣, 关欣, 桃李, 等.基于单机动平台的滑窗式最小二乘定位算法[J].中国电子科学研究院学报, 2015, 10(5):557-562.

[22]张政超, 童力.四站时差无源定位精度分析[J].中国电子科学研究院学报, 2010, 5(6):582-585.

孙 顺(1992—)，男，山东人，主要研究方向为无源定位、误差配准、信息融合；

E-mail:sunms7@qq.com

董 凯(1986—)，男，湖南人，博士，主要研究方向为雷达数据处理、系统仿真；

修建娟(1971—)，女，山东，博士，副教授，主要研究方向为无源定位、雷达数据处理；

刘 瑜(1986—)，男，湖南人，博士，主要研究方向为多传感器信息融合。

A Passive Source Localization Algorithm with Multiple Moving Observers Using TDOA/GROA Measurements Based on CWLS

SUN Shun, DONG Kai, XIU Jian-juan, LIU Yu

(Research Institute of Information Fusion, Naval Aeronautical andAstronautical University, Yantai 264001, China)

This paper proposes a algorithm to solve the problem of passive source localization with multiple moving observers using time differences of arrival (TDOA)and gain ratios of arrival (GROA)measurements.Traditional localization model introduces an intermediate variable to construct the linear equation, which is not suitable for the occasion of continuous localization with multiple moving observers.Therefore, a TDOA/GROA joint localization model without the intermediate variable is established for the problem.First, error items are derived on the basis of measurement model, generalized to all history measurements, and passive source localization algorithm based on constrained weighted least squares(CWLS)is proposed.Finally, target state estimation is obtained through generalized eigendecomposition of weighted matrix and constrained matrix.The proposed algorithm avoids redundancy caused by intermediate variable, doesn't require initialization process and has robuster performance.Simulation results indicate that the proposed algorithm achieves the Cramér-Rao lower bound (CRLB)and has an asymptotically unbiased solution.

source localization; constrained weighted least squares; time difference of arrival; gain ratio of arrival; intermediate variable

2016-06-18

2016-09-25

国家自然科学基金项目(61471379, 61102166, 91538201)

：A

1673-5692(2016)05-540-07