产业关联网络演变与影响机制研究——基于北京市12个年度投入产出表的分析

李 茂

产业关联网络演变与影响机制研究
——基于北京市12个年度投入产出表的分析

李 茂

产业关联网络的演变是产业经济研究的前沿问题。以北京市为例，利用该市12个年度的投入产出表构造产业关联网络模型，展示产业关联网络的演变格局，进而计算和比较产业关联网络模型拓扑特征的变化。通过计算与比较发现：产业关联网络的整体布局演变呈现稀疏化特征，网络的平均度和平均路径长度呈现“W”形变化，聚类系数演变显示出“M”形变化过程。进一步的机制分析发现，地区经济总量水平和地区专业化程度负向影响网络中节点连接强度，经济发展方式的转型升级对产业关联网络节点距离产生负向影响。地区经济外向型水平提升使得北京产业关联网络中的环向连接数量降低，导致网络连接的稀疏化问题。针对以上结论，最后给出有关产业经济发展的政策建议。

产业关联； 复杂网络； 拓扑特征； 演变； 影响机制

一 引 言

产业关联(Industrial Relations)是指经济活动中各产业之间存在和发生的广泛、复杂和密切的技术经济联系。这种联系以产业间的投入与产出、供给与需求的数量关系为主，反映着各产业间量的关系。各个产业在中间生产过程中相互影响、相互制约，构成一个动态系统。分析这一动态系统内部的关联状况，有助于深入了解各产业的发展水平，为各产业发展决策提供依据。Leontief(1936)[1]提出利用投入产出法分析产业关联，即通过编制投入产出表，建立相应的线性代数方程体系，综合分析和确定国民经济各产业之间错综复杂的联系。此后，产业关联一直是技术经济领域的研究热点(Hayter, 2015[2]; Fang, 2014[3]; Morris, 2011[4]等)。

随着经济发展水平提高和国民经济部类变化，产业之间的关联变得多样化和复杂化，传统的投入产出分析遇到了技术瓶颈：投入产出分析主要采用线性代数等理论，难以描述产业关联中的整体情况，也难以表述产业关联内部的集群关系、多元流向关系等。随着技术经济研究中跨学科理论的引入，学术界逐渐认识到可以利用复杂网络理论对产业关联进行研究，建立产业关联网络(Industrial Relations Network)理论。该理论对深入研究产业关联来说有重要的理论意义与实际价值：首先，有助于详细分析和阐释产业关联的内部结构、发展特征，以及一些重点关系；其次，有助于探究不同生产部类之间的联系，揭示产业发展过程中的内在规律，并通过可视化的形式展现产业关联网络的总体连接情况；最后，有助于拓宽学术界对产业关联的认识范围，加深对不同产业生产过程中技术联系的理解，同时为区域产业升级、产业转移以及产业集群发展提供理论支撑。

本文借鉴已有研究成果，以北京市为例，采用历时态的方法对产业关联网络进行比较分析，并对产业关联网络的演变影响机制进行深入探讨。与已有研究成果相比，本文创新点在于：首先，改进了产业关联网络模型的建构方法，综合考虑产业关联的实际情况，以北京市这一代表性地区为例，构造出产业关联有向有权网络模型，同时从实际情况出发提供一个更为准确地描述产业关联网络连接情况的方法。其次，采用历时态分析方法，分析产业网络的演变情况。全面而有重点地比较12个年度的北京产业关联网络的总体布局和拓扑特征，有助于提高对产业关联网络的认识水平。再次，利用计量模型研究产业关联网络演变的影响机制。最后，本文的研究结论有可能为北京产业升级和京津冀产业协同发展提供决策参考依据，在一定程度上推进其他地区的产业关联网络研究。

本文的内容结构安排如下：第一部分是引言；第二部分是文献综述；第三部分主要对现有产业关联的建模方法进行比较，重点探讨有关建模方法的改进；第四部分是数据来源与处理；第五部分是模型计算结果与分析，主要是北京产业关联网络的总体布局展示和拓扑特征比较；第六部分分析产业关联网络演变的影响机制；最后一部分是结论和政策建议。

二 文献综述

一般意义上，复杂网络是指由数量巨大的节点和节点之间复杂关系共同构成的网络结构*到目前为止，学术界还很难对复杂网络给出一个严格的定义，在这就不赘述不同的定义。但学术界普遍认为复杂网络具有网络规模庞大、连接结构复杂、时空演化过程复杂、多重复杂性融合等特征。。复杂网络理论与数学中的图论有着深厚联系，它们都是利用抽象的网络图结构来研究复杂系统的性质。20世纪60年代之后，复杂网络理论又引入了统计物理学、计算机、系统工程等学科的概念、范式和研究方法，逐步成为了一门以复杂系统为研究目标的交叉学科。对于复杂网络的研究，具有里程碑意义的研究成果如下表所示。

表1 复杂网络研究的代表性成果

随着研究的深入，学术界开始利用复杂网络理论来分析产业间的关联状况。Campbell(1972)[10]利用投入产出表构建产业图，并依据最小分割子图的数量分析产业集群水平。Slater(1977)[11]改进了Campbell的方法，利用1967年美国的投入产出表数据，以图论中的流模式方法识别了产业集群。赵炳新(1996)[12]利用图论模型研究了产业部门中的聚落群类和产业结构的演进规律。方爱丽等(2008)[13]提出了投入产出关联网络模型及其统计属性研究的基本方法与思路，并从复杂网络的视角出发建立各产业部门之间的投入产出关联复杂网络模型，利用国民经济核算司发布的投入产出数据分析投入产出关联网络的边权分布、强度分布和聚集系数等主要网络属性，进而揭示我国国民经济系统中各产业部门之间复杂的投入产出关联关系。刘刚和郭敏(2009)[14]在复杂网络范式下，以部门为节点、部门之间的投入产出直接消耗系数为连接边，建立中国宏观经济多部门网络，并在此基础上实证研究宏观经济多部门网络的拓扑性质。邢李志(2012)[15]通过投入产出理论建立反映区域产业结构演化的复杂网络模型，利用度分布、权分布和网络路径长度等概念对产业结构的网络拓扑特征进行分析。侯明和王茂军(2013)[16]利用2010年北京42个部门的投入产出数据，建立前向产业关联模型和后向产业关联模型，分析北京产业关联网络的一些特征性质。李茂(2016)[17]利用2012年北京42个部门的投入产出表，建立有向无权的产业关联网络模型，分析2012年北京产业关联网络的拓扑特征。

综上，前人在理论与应用方面的一些创新性研究，既丰富了复杂网络理论的内涵，也扩展了其实际应用，体现了很好的应用价值。然而，已有研究仍存在以下几个方面的问题：第一，分析了产业关联网络的某些拓扑特征，说明了其所属的复杂网络性质，但并没有揭示这些特征的产业经济学涵义；第二，有些研究以直接消耗系数矩阵为模型研究基础，但这种方法还不完善，不能反映出产业关联的内在特征，存在许多有待改进的地方；第三，已有研究均为对静态时点产业关联的考察，没有进行动态时点的分析，而通过比较不同时间点上的产业关联网络特点、拓扑特征与社团结构，可以挖掘产业关联的内部联系和动态变化。

三 建模方法与改进

(一)产业关联网络建模的基本方法

产业关联网络的建模基础是投入产出表。投入产出表分为价值型投入产出表和实物型投入产出表两种，价值型投入产出表以国民经济同类产品的集合为产业进行编制，用统一的货币单位反映各产业之间的投入与产出关系的表格。从现有研究成果来看，产业关联网络建模所使用的投入产出表均为价值型投入产出表，其一般形式见表2。

表2 价值型投入产出表的一般形式

如表所示，投入产出表的左上部分(也称为第一象限)Xij为中间产品象限(也称为基本流量表)，它是投入产出表的基本象限，反映国民经济各产业之间总体的经济技术联系。对于具体的xij，从横行看表示的是i产品分配给j产业做生产使用的价值量，从纵列看表示的是j产业生产中消耗的i产品的价值量。处于第一象限的Xij是一个n×n的矩阵，如果将不同的产业视为节点的话，那么对Xij矩阵进行一定的处理，可以构建起反映节点间联系的邻接矩阵。以邻接矩阵为基础，经过一定的改造可建立起一个以不同产业为节点，以它们之间的经济技术联系为连边的产业关联网络。

从上可知，产业关联网络的建模需要三大基础：第一，是完成编制的价值型投入产出表，这是搭建模型的基本材料；第二，由投入产出表中的不同部门代表不同节点(Nodes)；第三，利用一定的规则对中间产品象限Xij进行改造，以构造节点之间的连边(Edges or Arcs)。可以发现，投入产出表和投入产出表中的部门是外生的，是建模前就已经确定的，只有连边依赖于建模中连接规则。也就是说，不同的连接规则决定不同的连接数量与类型，进而对随后的分析和比较带来不同的结果。

(二)已有连接规则的比较

从现有研究成果来看，节点之间连接规则主要有以下几种方法，详见表3：

表3 有关连接规则的比较

从已有连接规则来看，可以发现以下经验：第一，两个部门之间的连边需要设定合适的阈值。否则产业关联网络就会成为一个全局耦合网络*全局耦合网络的拓扑特征为常数值，不具备演化研究意义。，阈值偏小会导致连边过于冗余，不利于分析产业关联中的显著关系，设定过高又会剔除部门之间的显著联系。第二，有向有权网络是较好反映产业关联中流量方向的模型。由于产业关联中不仅存在着前向关联、后向关联和环向关联，而且存在连接强度与大小的区别。因此，有向有权网络模型是比较贴切反映实际情况的模型。第三，产业关联网络模型中不应包含自环。产生自环的原因就是中间消耗矩阵或者直接消耗矩阵对角线元素没有消除。由于产业关联网络模型的理论前提就是节点不存在自环关系，因此部门内部的投入产出关系不在产业关联网络研究视阈之内。

(三)对连接规则的改进

基于已有研究成果，本研究对连接规则作以下改进：

第一，以完全消耗系数矩阵Bij作为邻接矩阵构造的基础。之所以选择完全消耗系数矩阵，是因为在产业关联网络中各种产品在生产过程中除有直接的生产联系外，还存在间接的联系；各种产品间的相互消耗除了直接消耗外，还存在间接消耗。完全消耗系数则是对这种直接消耗和间接消耗的全面反映。与直接消耗系数相比，完全消耗系数揭示了部门之间的直接联系和间接联系，因而它能更全面、更深刻地反映出部门之间相互依存的数量关系。完全消耗系数矩阵由直接消耗系数矩阵Aij计算得出，而直接消耗系数矩阵由第一象限的Xij计算得出。

第二，剔除对角线元素设定关联阈值。如前所述，阈值的设定不能偏小，不然会带来连边冗余，使得重要关系被繁芜的联系所“掩盖”。一些研究不剔除不显著的关系，完全利用直接消耗矩阵去构造邻接矩阵，带来了模型中节点连接的冗余问题。同样，阈值的设定又不能偏大，否则就会剔除某些重要关系，导致连边“失真”。在已有研究中，一些阈值的设定，考虑了中间消耗矩阵或者是直接消耗矩阵对角线元素，却带来设定值较高的问题。因此，关联阈值的选取十分重要。借鉴已有研究，本文采用以下方法选取阈值：

计算得到完全消耗系数矩阵Bij后，设定两个节点i，j之间的连接阈值Θ为完全消耗系数矩阵中剔除了对角线元素后的剩余元素的平均值①，即：

(1)

第三，为了保留产业关联中的前向、后向与环向关联信息，本文采用有向有权网络模型。这样就能使得产业关联中的价值流向在总体布局图中显现出来，给研究者以直观的印象。为了保留两个不同节点(代表两个不同的生产部门)的中间投入消耗关系(连边方向)，Bij不做上三角矩阵化和对称矩阵化处理*换言之，Bij中的元素bijj来和bji具有不同含义。前者表示，i产品分配给j产业做生产使用所消耗的完全价值量，反映了前向关联，后者表示是j产业生产中消耗的i产品的完全价值量，反映了后向关联。一般而言，bijj≠bji。。为了保留两个不同节点(代表两个不同的生产部门)之间的连接强度信息(边权)，以上式的Θ为阈值将Bij转化为邻接矩阵Eij，转化公式如下：

(2)

从式(2)可以看出，大于阈值的节点连接(部门之间的完全消耗系数)被保留下来，并作为连接的权重，小于阈值的连接信息被剔除，从而最大效果地保留了产业关联中部门联系的信息。

由以上讨论，本文提出的模型建构规则主要有以下几个：(1)选取投入产出表的中间消耗矩阵作为基础材料；(2)将投入产出表中n个不同部类视为n个不同的节点；(3)利用中间消耗矩阵去计算Leontief逆矩阵，进而得到完全消耗矩阵Bij；(4)设定两个节点i，j之间的连接阈值Θ为完全消耗系数矩阵Bij中剔除了对角线元素后的剩余元素的平均值；(5)以Θ为阈值将Bij转化为邻接矩阵Eij，构造出产业关联网络模型G(n,Eij)。

四 数据来源和模型建构

(一)数据来源

本文所用的北京市投入产出表来自“北京2012年投入产出调查网” (http://www. bjstats.gov.cn/2012trcc/)中的“历史数据”专栏。北京市投入产出数据最新截止到2012年，该数据于2014年10月公布。采集的投入产出表数据的年份是1985年、1987年、1990年、1992年、1995年、1997年、2000年、2002年、2005年、2007年、2010年、2012年等12个年份。

由于统计口径的变化，1985年北京投入产出表包含68个部门；1987年、1990年、1992年、1995年北京投入产出表包含33个部门；1997年和2000年北京投入产出表包含40个部门；2002年、2005年、2007年、2010年和2012年北京投入产出表包含42个部门。

(二)数据处理

利用投入产出表中的基本流量表可以计算出Leontief逆矩阵(I-Aij)-1，Leontief逆矩阵减去单位矩阵I可得到完全消耗系数矩阵Bij，计算公式如下：

Bij=(I-Aij)-1-I

(3)

(三)模型建构

按照前面改进的方法，将投入产出表中n个不同部类视为n个不同的节点。利用中间消耗矩阵去计算Leontief逆矩阵，进而得到完全消耗矩阵Bij。设定两个节点i，j之间的连接阈值Θ为完全消耗系数矩阵Bij中剔除了对角线元素后的剩余元素的平均值。以Θ为阈值将Bij转化为邻接矩阵Eij，这样可以建构12个不同年度的北京产业关联网络模型。为了区别，分别命名为G1985(n,Eij)、G1987(n,Eij)、……G2012(n,Eij)。

五 以北京市为例的产业关联网络演变

(一)整体布局演变

利用网络分析软件Pajek绘制出12个年度的北京产业关联网络整体布局情况。为了便于比较，布局方法采用学术界通用的镰田—河合(Kawada-Kawai)方法。整体布局演变情况如下：

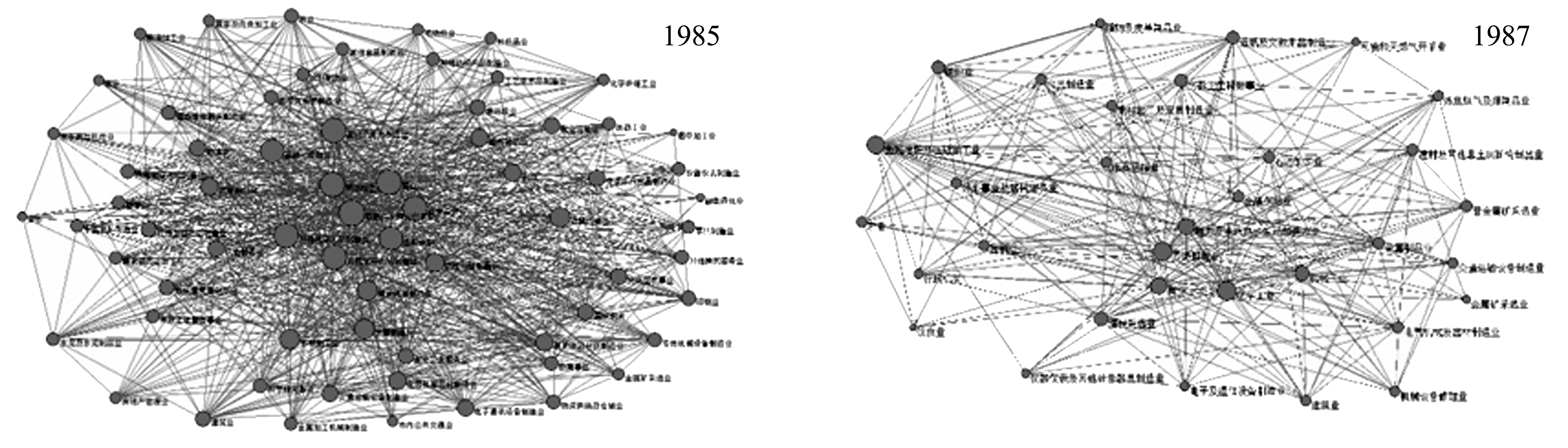
由图1*由于关联网络图中节点较多且较复杂，如需更清晰的图片可与作者联系。可见，除了节点数量有着不同之外，北京市产业关联网络的整体布局演变呈现出一个显著的特征：即在具体布局上经历了一个“密集—稀疏—密集—稀疏”的演变过程，但在总体布局上呈现出稀疏化趋势。下面用具体的拓扑特征去表述这种演变过程。

(二)拓扑特征的演变

复杂网络具有规模庞大、连接结构复杂、时空演化过程多样、多重网络复杂性融合的特点，这些特点统称为复杂网络的拓扑特征，学术界主要采用指标描述的方式去刻画这些特征。参照Albert和Barabási(2002)[8]的研究，本文所要计算的拓扑特征主要有以下3类(见表4)。

②需要指出的是，节点i的度Ki定义为与节点i直接相连的边的数目，网络中所有节点的度的平均值称为网络的平均度。在模型中，每个节点的度是由Pajek 程序计算得出的。

③dij定义为连接i节点与j节点的最短路径上的边的数目，而i节点与j节点最短路径指的是连接这两个节点的边数最少的路径。在模型中，dij是由Pajek 程序计算得出的。

④ 在模型中，节点i 的Fi 是由Pajek 程序计算得出的。

利用复杂网络分析软件Pajek软件对数据进行计算，12个年度的拓扑特征演变情况如表5及图2、图3、图4所示：

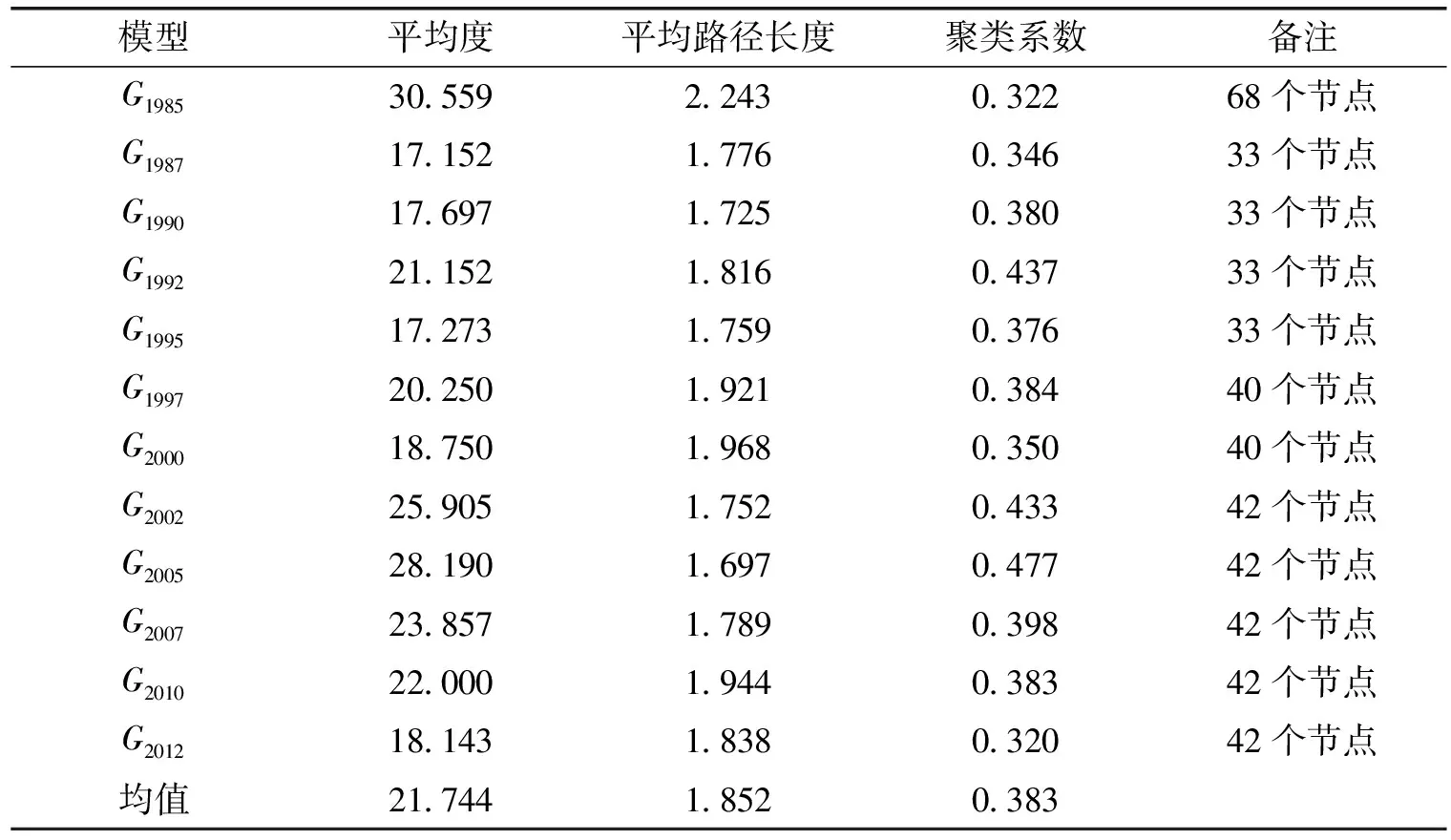
表5 模型拓扑特征演变情况

图2 北京产业关联网络平均度演变情况

图3 北京产业关联网络平均路径长度演变情况

图4 北京产业关联网络聚类系数演变情况

(三)对于拓扑特征演变的解释

根据定义，平均度反映的是网络中节点的平均联系强度。因此，产业关联网络的平均度代表了不同产业部类(节点)之间的显著联系程度。从图2可以发现，北京产业关联网络的平均度经历了一个“降低—增高—降低”的“W”形趋势。1985年，北京产业关联网络中每个产业平均与30个产业有着显著联系，而1995年降低到17个，随后经历了一定幅度的回升再降低的过程，到2012年，每个产业平均与18个产业存在着显著的联系，这说明北京市产业关联整体强度呈现下降趋势，不同产业在中间生产过程中联系程度正在降低。

对于这种演变的一个解释是，随着产业经济水平不断升级，北京地区企业面临的需求日益多样化，而生产经营中的分工日益具体化，竞争强度越来越大，企业普遍追求专业化而不是范围经济。因此，由企业带动的产业专业化水平逐渐提高，行业之间的显著关联范围逐渐变小。

平均路径长度代表了网络中任意两个节点之间距离的平均值。在产业关联网络中，平均路径长度就代表任意两个生产部类之间的间隔距离。平均路径长度较高，表明生产部类之间的间隔就越大；反之则表示生产部类之间的间隔较小。北京市产业关联网络的平均路径长度为1.851，表明任意两个产业之间距离不超过2，即任意两个产业之间通过1个产业就可以产生显著联系，具备明显的“小世界”特性。图3显示，北京市产业关联网络的平均路径长度经历了一个“降低—增加—降低”的“W”形的过程，表明这十年来北京市产业内部关联呈现出“稀疏—紧凑—稀疏”的态势。

造成这种演变态势的主要原因可能是北京经过承办2008年奥运会等活动之后，城市发展水平上升到了一个新高度，经济增长方式大幅转变：科技创新与文化创新成为北京经济发展的新“引擎”，文化创意产业和生产性服务业成为主导产业，总体经济实力又得到了进一步增强。在此进程中，许多传统行业如轻重制造业等转移、转型，取而代之的是人力资本含量更高的生产性服务业和文化创意产业，这些产业在生产过程中要素流通更为频繁，第三产业集群内部的相互供给强度不断提高，产业间的“集聚—放大—影响”的作用逐步显现。但北京市新兴产业群还处在产业周期的初级阶段，产业集群雏形初现，产业带动能力有限，集聚效应不明显，产业联动发展空间还比较大。

聚类系数反映的是与某一个节点连接的其他节点之间的连接程度，是考察节点之间集聚的重要指标。在产业关联网络中，聚类系数反映的是不同生产部类之间环向关联的程度。产业关联网络的聚类系数高，表明与某一个生产部类连接的其他部类之间具有较为紧密的联系。聚类系数低说明与某一个生产部类联系的其他部类之间不存在紧密联系关系。也就是说，产业关联网络中的环向关联度较低，产业链的技术经济联系结构比较简单，基本上属于“直线型”；聚类系数高说明环向关联紧密，产业链通过复杂的技术经济联系构成一个“环”，结构上趋于“环线型”。图表显示，北京市产业关联网络中的聚类系数经历了一个“增加—降低—增加—降低”的“M”形过程，在2005年聚类系数达到了最大值。

究其原因，北京经济逐步转为外向型经济，越来越多的生产要素和中间产品由外地供应，对区域内产业中间产品的依赖度逐渐降低，加上服务贸易和服务外包发展水平不断提高，基础设施建设日趋完善，物流产业发展日益加快，流通成本大大降低，这些因素均促使北京区域内的产业逐步通过北京区域外的市场为自身提供中间产品，内部环向关联程度大大降低。

六 影响机制分析

(一)研究思路与模型选择

为了揭示推动北京产业关联网络演变的核心因素，需要选择合适的计量工具进行因果判定。从现有研究方法来看，经济科学经验研究中的因果判定主要有以下几种方法：多元线性回归(MLR)、机器学习(ML)、鲁宾因果模型(Rubin’s Casual Models)、结构模型(SM)、充分统计量法(SS)等。尽管它们的具体方法和适用对象不尽相同，但本质上都是在寻找可信的对照组，利用不同控制条件下的对照组数据进行计算，进而做出因果推定。但如果变量之间没有理论联系，或者不存在结构支撑，则可用向量自回归模型(Vector Auto-Regression Modle, VAR)分析数据。向量自回归模型考虑到了数据的统计学性质，能够更好地分析数据之间的关系。它把系统中每一个内生变量当作所有内生变量的滞后值的函数，从而将单变量自回归模型扩展到了由多元时间序列变量组成的“向量”自回归模型，即扩大了数据之间关系的分析能力。并且VAR模型具有很强的包容性和扩展性，如在一定的条件下，滑动平均模型和自回归滑动平均模型也可以转化成向量自回归模型，因而受到越来越多研究者的青睐。

有学者利用VAR模型特点对影响因素进行了甄别。比如，苏方林等(2010)[21]利用加权最小二乘法与向量自回归方法，对比性地建立广西碳排放量及影响因素间关系的实证模型，并进一步利用脉冲响应函数和方差分解探索影响系数大小和时期变化规律。罗孝玲等(2012)[22]以2001-2010年的季度数据为样本，定量地描述了各宏观因素对房地产价格的影响程度,并利用脉冲响应函数和方差分解分析各个因素对房地产价格的影响时滞、持续时间和作用强度。刘海兵和刘丽(2009)[23]在建立向量自回归模型的基础上，运用脉冲响应函数和方差分解方法对中国居民消费价格指数的影响因素作实证分析。

选择向量自回归模型分析产业关联网络演变的影响机制有以下几点优势：第一，尝试深入分析影响产业关联网络演变的内在因素，利用VAR模型识别产业关联网络演变和诸多解释变量之间的关系；第二，向量自回归模型对结构、规模较小的数据具有良好的计量效度。本研究中数据规模有限，向量自回归模型比较适应实际情况；第三，向量自回归模型对数据质量的要求不是很高，可以较好地处理序列数据，而且参数的估计比较容易，这种特性保证了模型分析的信度。

(二)变量与数据来源

采用上文分析的平均度、平均路径长度和聚类系数作为北京产业关联网络拓扑特征演变的变量。参考已有研究成果，通过德尔菲法获取影响因子，选择以下变量为北京产业关联网络演变的影响因素，将地区人均GDP等解释变量引入。表6列出了各变量及其含义、数据来源与描述性统计情况。

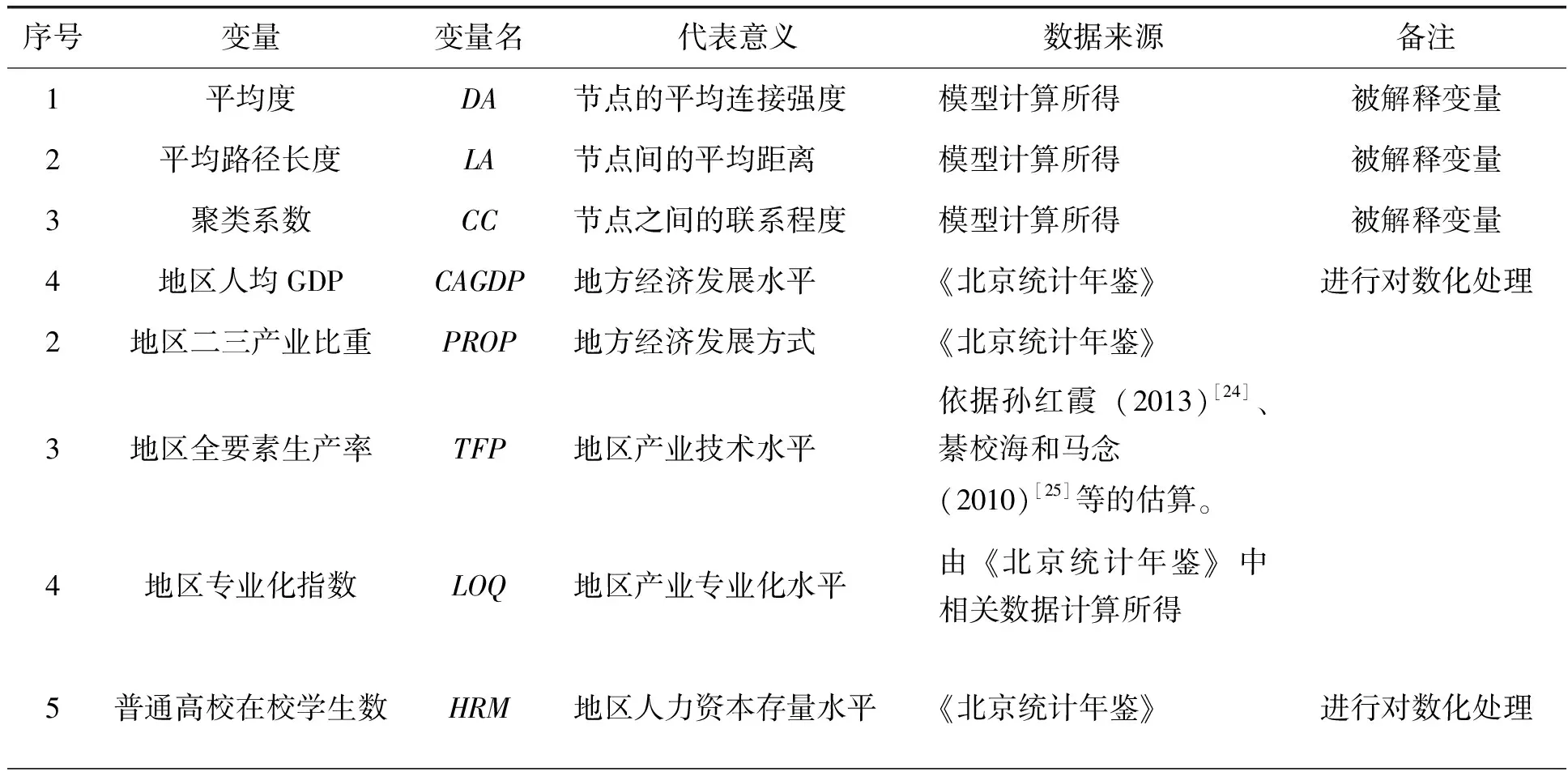
表6 变量含义与数据来源

(续上表)

序号变量变量名代表意义数据来源备注6货运周转量TFT反映国内贸易水平《北京统计年鉴》进行对数化处理7外贸贡献率CRF反映地区经济开放程度《北京统计年鉴》

注：地区专业化指数是评价地区专业化部门综合发展程度的指标,其计算方法为:设某地区有几个专业化部门(或生产部门),每部门占全地区产值的比重为Yi,则专业化指数:X=nY1+(n-1)Y2+(n-2)Y3+…+[n-(i-1)]Yi+…+Yn，式中Y1、Y2、…Yn按由小至大顺序排列。

表7 变量的描述性统计情况

(三)运算过程与结果

不考虑变量的性质，先建立初步的向量自回归模型。本文首先利用滞后阶数为2的向量自回归模型作为初步分析模型。其中，VAR1模型是包含DA、CAGDP和LOQ3个变量的向量自回归模型；VAR2模型是包含LA、TFP、PROP和HRM4个变量的向量自回归模型。VAR3模型是包含CC、TFT、CRT3个变量的向量自回归模型*限于篇幅，三个向量自回归模型的解释式不在此列出。。

随后，利用Eviews软件对模型的滞后阶数进行检验，基于AIC和SC最小化原则选择滞后阶数，最终选取滞后阶数为2阶，并进行格兰杰因果检验。检验结果如下：

表8 VAR1模型的Granger因果检验结果

注：***表示在1%的显著性水平上显著。表9、表10同。

表9 VAR2模型的Granger因果检验结果

表10 VAR3模型的Granger因果检验结果

检验结果显示，在1%的显著性水平下，CAGDP和PROP是DA的格兰杰原因，反之不成立；在1%的显著性水平下，PROP、TFP是变量LA的格兰杰原因，HRM不是变量LA的格兰杰原因，反之不成立；在1%的显著性水平下，TFT和CRF是变量CC的格兰杰原因，反之不成立。

明确了各变量的滞后阶数和因果关系之后，在VAR1模型、VAR2、VAR3模型的基础上，剔除变量HRM，确立新的滞后阶数，重新构建VAR1*、VAR2*和VAR3*模型。对这三个模型进行AR根检验发现，所有根模的倒数小于1，处在单位圆之内，说明VAR1*、VAR2*和VAR3*模型是稳定的。

以上是对影响因素的定性研究，下面利用向量自回归模型的脉冲响应工具对影响因素的定量影响程度进行研究。脉冲响应函数分析法可以测量一个内生变量对由误差项所带来的冲击的反应，即在随机误差项上施加一个标准差大小的冲击后，对内生变量的当期值和未来值所产生的影响程度。本文利用这一分析技术，得到VAR1*、VAR2*和VAR3*模型的脉冲响应结果。

由图5可以看出，当本期给CAGDP一个正冲击后，DA在第一期的响应为负值，后在第2期转为正值达到最高点，但冲击程度有限(值为0.0543)；当在本期给LOQ一个冲击后，DA会在第二期达到最高水平(值为0.0371)，然后缓慢下降。当期CAGDP的变化在第一期是反向带动DA的变化，而在第二期后则可以同向带动DA的变化。这表明地区经济发展水平对于产业关联网络的平均度演变总体上有着正向影响，经济发展水平越高，产业部类之间中间投入消耗强度就越大，产业关联网络中节点的联系强度就越大。当期LOQ的变化在第2期后才能对DA产生正向拉动作用，这说明了地区专业化程度越高，国民经济生产分工就越详细，产业间联系强度就越高。但随着时间的推移，CAGDP和LOQ的推动作用很快转为负值，造成这方面现象的原因可能是：随着经济发展水平的提高和专业化水平的提升，产业关联网络内部形成了一些相对独立“聚落群类”(也就是现实中的产业群)，聚落群类内部联系越发紧密，但产业关联网络整体上联系强度却在降低，平均度在降低。

图5 VAR1*模型的脉冲响应分析图

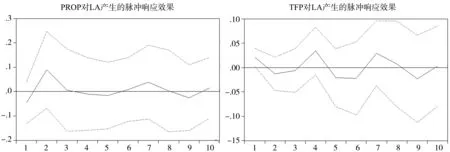
图6 VAR2*模型的脉冲响应分析图

图7 VAR3*模型的脉冲响应分析图

由图6可以看出，当本期给PROP一个正冲击后，LA在第一期的响应为负值，后在第2期转为正值并达到最高点，但冲击程度为0.081。TFP的变化可以带动当期LA的同向变化。但PROP和TFP在后期中的影响效果却呈现波浪状变化。由于PROP和TFP是代表了经济发展方式的变量，可以尝试得出这样的结论：随着经济发展方式的转变，整个产业关联网络间节点的距离正在变小，存在显著联系的生产部门间的联系长度正在缩小，即“隔行不再如隔山”，但这种影响程度是随着时间发展而起伏的。

由图7可以看出，当本期给TFT一个正冲击，CC在第一期的响应即为最大值(值为0.136)，而且这种影响将一直持续下去。而CRF对于CC的影响在第二期才能显现出来，但这种影响幅度较小，平均值只有0.023左右。TFT代表的是地区国内贸易发展程度，CRF代表是地区国际贸易发展程度，可以发现：随着北京经济外向型程度的提高，越来越多的生产要素和中间产品由外地供应，而北京主要提供创意产品和生产指导服务，“小而全”的生产加工经济逐步向“强而精”的总部经济转型，对区域内产业中间产品的依赖度逐渐降低。

七 结论与政策建议

(一)研究结论

综合上述分析，北京市产业关联网络演变情况如表11所示：

表11 北京产业关联网络演变情况

第一，从总体上来看，北京市产业关联网络的平均度呈现出“W”形变化。北京市产业关联网络呈现出稀疏化的发展态势，节点之间的连边数量不断减少，网络密度逐步降低。其主要原因是，北京市产业经济的外向型程度不断加深，对本地产业生产的中间产品的依赖度越来越低。

第二，北京市产业关联网络的平均路径长度为1.852，且经历了一个“降低—增加—降低—增加”的过程，经济发展方式的提升对于网络平均路径长度产生负向影响。北京市产业关联网络聚类系数经历了“M”形的变化，说明在北京产业关联结构中直线型的关联结构(前向关联和后向关联)已成为其主要结构，环向结构越来越稀疏，北京市已经形成了稳定的外向型经济结构。

第三，进一步的影响机制研究发现，北京地区经济总量水平和地区专业化程度负向影响网络中节点连接强度，第三产业占比和TFP(全要素生产率)所代表的北京经济发展方式的转变对产业关联网络中的节点距离产生负向影响。地区经济外向型水平提升造成产业关联网络中环向连接数量的降低，带来网络连接的稀疏化。

(二)政策建议

第一，观察北京产业关联网络近几年的布局，文化创意产业与生产性服务业(如文化、体育与娱乐业，信息传输与信息服务业、科研与技术服务业等)还处在网络中的边缘位置，对产业关联的影响力有限。北京需要加强文化创意产业与生产性服务业在产业关联网络中的地位，发挥其价格信号传导作用，提高北京地区人才、技术、信息的使用效率，形成重点产业群，做大做强“总部经济”，实现京津冀产业协同发展。

第二，通过研究北京产业关联网络布局演变可以发现，对于处在产业关联网络边缘的产业，如冶金、机械制造、服装加工、食品加工、印刷包装、木材加工等传统制造业，应加大产业转移力度。在产业转移的过程中，应提高和增强区域产业转移主体的市场运作能力，加强转移出去的企业的经营体制改革，培育适应市场经济要求的企业主体。

第三，在产业关联网络布局演变中，电力、热力的生产和供应业、燃气生产和供应业和水的生产和供应业一直处在北京产业关联网络的拓扑中心位置，价格传导作用十分明显。因此，这些行业的能源使用效率和清洁排放水平直接影响整个北京产业的能源使用效率和绿色环保水平。应提高北京市电力、燃气和水生产供应业的技术水平和管理水平，提升能源利用效率，这是优化北京市产业能源结构的一项重要举措，对于提高北京产业的整体能源利用效率、建设生态城市有重要意义。

[1] Leontief , W. W.. Quantitative Input and Output Relations in the Economic Systems of the United States[J].TheReviewofEconomicStatistics, 1936, 18(3): 105-125.

[2] Hayter, S.. Introduction: What Future for Industrial Relations?[J].InternationalLabourReview, 2015, 154(1): 1-4.

[3] Fang, L. C.. Chinese Industrial Relations Research: In Search of a Broader Analytical Framework and Representation[J].AsiaPacificJournalofManagement, 2014, 31(3): 875-898.

[4] Morris, H.. What’s the Point of Industrial Relations? In Defence of Critical Social Science[J].BritishJournalofIndustrialRelations, 2011, 49(49): 404-406.

[5] Erdös, P., Rényi, A.. On Random Graphs I[J].PublicationesMathematicae, 1959, 6: 290-297.

[6] Watts, D. J., Strogatz, S. H.. Collective Dynamics of “Small-world” Networks[J].Nature, 1998, 393(6684): 440-442.

[8] Albert, R., Barabsi, A. L.. Statistical Mechanics of Complex Networks[J].ReviewofModernPhysics, 2002, 74(1): 47-97.

[9] Li, X., Jin, Y. Y., Chen, G.. Complexity and Synchronization of the World Trade Web[J].PhysicaA:StatisticalMechanicsanditsApplications, 2003, 328(1): 287-296.

[10] Campbel, J.. Application of Graph Theoretic Analysis to Inter-industry Relationships: The Example of Washington State[J].RegionalScience&UrbanEconomics, 1975, 5(1): 91-106.

[11] Slater, P. B.. The Determination of Groups of Functionally Integrated Industries in the United States Using a 1967 Inter-industry Flow Table[J].EmpiricalEconomics, 1977, 2(1): 1-9.

[12] 赵炳新. 产业关联分析中的图论模型及应用研究[J]. 系统工程理论与实践, 1996, 16(2): 39-42.

[13] 方爱丽, 高齐圣, 张嗣瀛. 投入产出关联网络模型及其统计属性研究[J]. 数学的实践与认识, 2008, 38(9): 34-38.

[14] 刘刚, 郭敏. 中国宏观经济多部门网络及其性质的实证研究[J]. 经济问题， 2009, (2): 31-34.

[15] 邢李志. 基于复杂网络理论的区域产业结构网络模型研究[J]. 工业技术经济, 2012, 31(2): 19-29.

[16] 侯明, 王茂军. 北京市产业网络结构的复杂性特征[J]. 世界地理研究, 2014, (2): 123-132.

[17] 李茂. 北京产业关联网络的拓扑特征研究[J]. 北京社会科学, 2016, (5): 57-67.

[18] 张许杰, 刘刚. 基于复杂网络的英国产业结构网络分析[J]. 商场现代化, 2008, (9): 151-152.

[19] 王茂军, 杨雪春. 区域产业关联网络结构的复杂性分析——以四川省为例[R]. 中国地理学会百年庆典学术论文摘要集, 2009.

[20] Bechter, B., Brandl, B.. Measurement and Analysis of Industrial Relations Aggregates: What is the Relevant Unit of Analysis in Comparative Research?[J].EuropeanPoliticalScience, 2015, 14(4): 422-438.

[21] 苏方林, 宋帮英, 侯晓博. 广西碳排放量与影响因素关系的VAR实证分析[J]. 西南民族大学学报(人文社科版), 2010, 31(9): 140-144.

[22] 罗孝玲, 洪波, 马世昌. 基于VAR模型的房地产价格影响因素研究[J]. 中南大学学报(社会科学版), 2012, 18(4): 1-7.

[23] 刘海兵, 刘丽. 基于VAR模型的CPI影响因素分析[J]. 云南财经大学学报, 2009, 25(1): 119-124.

[24] 孙红霞. 北京地区三大产业全要素生产率的估算[J]. 现代管理科学, 2013, (10): 64-66.

[25] 綦校海, 马念. 我国东部发达地区全要素生产率探析——基于北京、 上海1978-2008年的数据[J]. 华东经济管理, 2010, 24(8): 51-55.

[引用方式]李茂. 产业关联网络演变与影响机制研究——基于北京市12个年度投入产出表的分析[J]. 产经评论, 2016, 7(6): 50-66.

The Evolution of Industrial Relations Network and the Influence Mechanism——Based on Beijing 12 Years’ Input-output Table

/2

The evolution of industrial relations network is the frontier of industried economics research. This paper constructs Beijing industrial relations network models using 12 years Beijing Input-Output table, shows the evolution of Beijing industrial relations network, calculates and compares the change in the topological characteristics of network. The paper points that the evolution of Beijing industrial relations network layout is a sparsification process, the change of the network’s average degree and the average path length exhibits a “W” shape process, the change of clustering coefficient of exhibits an “M” type process. Further analysis of the mechanism indicates that, the Beijing total economy and industry specialization negatively influences the average degree, the changes to the upgrade of economic development negatively affects the average path length, the degree of export-oriented of economy positively influences clustering coefficient. With these findings, the paper concludes with some policy suggestions for Beijing industrial economy development.

industrial relations; complex network; topological characteristics; evolution; influence mechanism

2016-08-03

北京市社会科学院2017年青年课题“京津冀地区产业关联网络研究”(项目编号：2016B3672，项目主持人：李茂)。

李茂，博士，北京市社会科学院市情调研中心助理研究员，研究方向为产业经济学与技术经济学。

F121.3

A

1674-8298(2016)06-0050-17

[责任编辑：郑筱婷]

10.14007/j.cnki.cjpl.2016.06.005