永磁直线同步电机的PIDNN控制
2017-01-04蔡满军赵晓东赵成圆
蔡满军,赵晓东,赵成圆
(燕山大学河北省工业计算机控制工程重点实验室,河北 秦皇岛 066004)
永磁直线同步电机的PIDNN控制
蔡满军,赵晓东,赵成圆
(燕山大学河北省工业计算机控制工程重点实验室,河北 秦皇岛 066004)
针对以永磁直线同步电机为执行机构的驱动系统容易受到端部效应等周期性扰动影响的问题,采用了基于PID神经元网络(proportional-integral-derivative neural network,PIDNN)的控制方法,通过定义具有比例、积分、微分功能的神经元,从而将PID控制规律融合进神经元网络中,有效地抑制端部效应、纹波推力、齿槽力和摩擦力对系统的干扰。仿真实验表明,与传统的PID控制相比,PIDNN控制提高了系统的鲁棒性和跟踪性,更加实用有效。
永磁直线同步电机;PID神经元网络;神经网络;干扰抑制
永磁直线同步电机(PMLSM)是一种能将电能直接转换成直线运动机械能而不需要任何中间转换机构的装置,与旋转电机相比,PMLSM在精度、快速性、耐久性等方面具有优势[1]。同时,正是由于缺少中间环节,各种干扰,如齿槽力扰动、纹波推力扰动等直接影响电机性能,大大降低电机的伺服性能。
为解决复杂系统的控制问题,中外学者进行了大量的研究工作。文献[2]采用了带滑膜观测器的控制方法,对PMLSM调速系统进行分析。文献[3]将模糊控制与传统PID相结合来设计控制器,比传统PID控制对外界有更好的鲁棒性,文献[4]结合了模糊控制和神经网络的优点来设计控制器,对外部干扰具有比较好的鲁棒性。文献[5]采用快速终端滑模来提高控制器的响应速度。文献[6]将重复控制与滑模控制相结合来提高控制器的控制精度。
基于以上分析,本文在传统PID和神经网络的基础上,提出了基于PIDNN的控制方法。对于一般的BP神经网络控制器需要通过离线学习得到优越的效果,而PIDNN是动态型的网络,其控制器具有简单且规范的拓扑结构。在实验平台上进行对比实验,结果表明,PIDNN控制有效地提高了系统的鲁棒性和跟踪性,能有效地抑制干扰,更加实用有效。
1 PMLSM的数学模型
PMLSM的机械运动方程为

式中:x为电机位移;Fcogging(x)为电机所受的齿槽力,与电机位移x有关;M为电机质量;B为粘滞摩擦系数;Ffriction(v)为电机所受的摩擦力。
由以上可得矢量控制下,采用id=0的控制策略时,PMLSM在d-q坐标系下的动力学方程为

式中:Kf为电机的反电动势系数。
纹波推力在数学模型中对Kf有影响,关系如下:
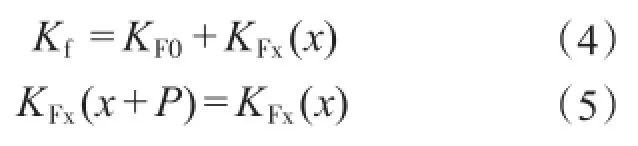
式中:KFx(x)为极距P的周期函数;KF0为平均电磁推力系数。
齿槽力和端部效应在永磁直线同步电机数学模型中主要体现在齿槽力Fcogging(x)上,Fcogging(x)也为相邻永磁体之间的距离P的周期函数,其数学描述为

Fcogging(x)和KFx(x)可以近似等效为一系列谐波函数的加权和,其模型如下:

其中未知权重

基函数为

式中:q1,q2为基函数Sc(x),SK(x)的谐波个数。
摩擦力的模型可描述为
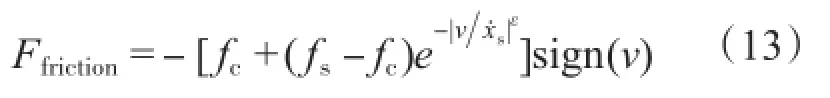
式中:fs为静态摩擦力;fc为库仑摩擦力;为经验系数。
用1个近似摩擦力曲线的连续函数Ff(v)来代替,其幅值为Af,则转换后的Ffriction为

加入扰动分析后的永磁直线同步电机的d-q数学模型可表示为
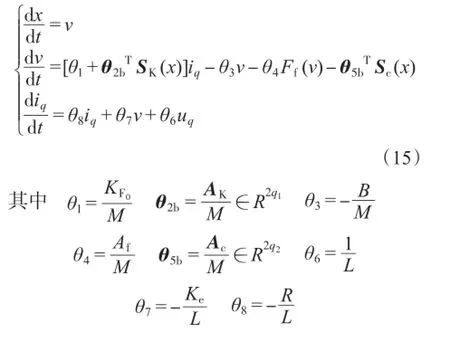
2 PMLSM的控制器设计
2.1 PID神经元网络
PID神经元网络(PIDNN)是1个3层前向神经元网络,为2×3×1结构,它的输入层有2个神经元,接受外部信息;它的隐层有3个神经元,分别为比例元、积分元和微分元,完成比例、积分和微分运算;它的输出层只有1个神经元,完成控制规律的综合和输出[7]。
2.2 PIDNN控制器的设计
2.2.1 神经元网络的算法
PID神经元网络控制器的设计主要包括前向算法设计、反传算法设计和初始值的选取。
2.2.1.1 前向算法设计
设v*为速度给定,v为电机实际速度,PIDNN的输入层的2个神经元在任意采样时刻k的输入分别为
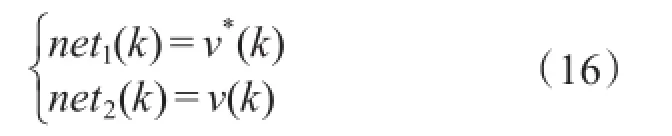
式(9)中的输出经过状态函数作用后为

式中:i=1,2。
输入层神经元的输出为

式中:j=1,2,3。
PIDNN的隐含层每个神经元各自的输入为

式中:wij为输入层至隐含层的连接权值。
式(18)分别经过各自神经元的状态转移函数后的输出为

经过输出函数作用后的输出为

PIDNN的输出层只包含有1个神经元,其输入为

式中:wj′为隐含层至输出层的连接权重值。
式(24)经过其神经元的状态转移函数后的输出为

输出层神经元输出为式(23),而PIDNN的输出u(k)就等于输出层神经元的输出,即

2.2.1.2 反传算法设计
PIDNN训练和学习的目的是使网络的实际输出和理想输出之间的偏差平方均值为最小,即
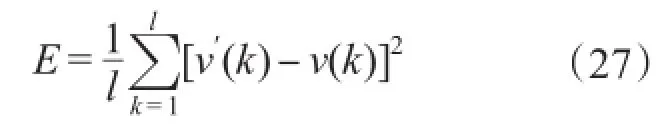
假设经n0步训练和学习后,各个神经元之间权值的迭代公式为

隐含层至输出层权值和输入层至隐含层权值的具体计算方法如下。
隐含层至输出层的权值迭代公式为

式中:wj′(n0+1)为隐含层至输出层的权重值。

输入层至隐含层的权重值迭代公式为
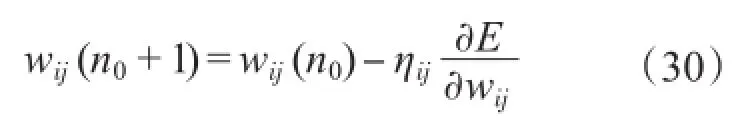
2.2.2 PIDNN的初始值选取
神经元网络连接权重的初始值决定了整个网络的学习方向和收敛速度。
为了使比例元、积分元和微分元的作用等价于PID控制器输出,选取w1j=+1,w2j=-1,输出层神经元为比例元,并且隐含层中比例元、微分元、积分元到输出层的连接权值分别为w1′=KP,w2′=KI,w3′=KD,可求出输出层神经元的输入总和为

可得到PIDNN连接权重取初值时的网络输出为

3 实验分析
本文通过LabVIEW设计了2种控制算法:PID控制算法和PIDNN控制算法,它们是以子Vi的形式被调用。
本实验平台的整体框架如图1所示,该平台以NI CompactRIO为核心,宏观上对永磁直线同步电机采用转速电流双闭环控制策略,其中电流环在驱动器中完成,采用PI控制策略;速度环在NI CompactRIO中完成。

图1 实验平台整体架构Fig.1 Experimental platform overall framework
速度环的速度电压参考输入由图1中的PC给定,其中电压与速度的转换关系为1V=310mm/s,可在驱动器中设定。驱动器的模拟输出口将速度转换为电压后经模块NI9223反馈提供给速度控制器,速度控制器的输出通过模块NI9263传给驱动器的模拟输入口,经过转换作为驱动器电流环的电流命令(current command),其中电压与电流的转换关系为1 V=1.13A。电机的实际速度通过驱动器进行采集并在PC中显示。
对比图2和图3可以看出,在同样的速度给定下,PIDNN控制器的调节时间为0.2 s,PID控制器的调节时间为0.4 s;在稳态时,PIDNN控制器下速度波动范围为112~128 mm/s;而PID控制器下速度波动范围为102~137 mm/s,可见PIDNN的控制效果要优于PID。

图2 PID控制下的速度响应曲线图(由驱动器采集)Fig.2 PID control speed response curve(collected by the drive)
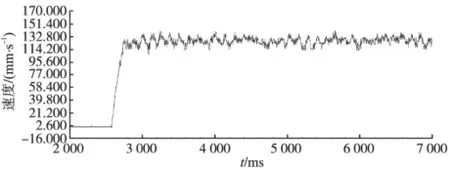
图3 PIDNN的速度响应曲线(由驱动器采集)Fig.3 PIDNN velocity response curve(collected by the drive)
4 结论
针对永磁直线同步电机的干扰抑制的问题,在传统PID和BP神经网络的基础上,采用了PID神经元网络控制方法。PIDNN能结合PID控制和神经网络控制的优点,具有简单、规范的拓扑结构,配合使用的权重初始值的选取规则和本身的动态性,能够得到更好的干扰抑制效果。仿真实验表明,与传统的PID控制和神经网络控制相比,PIDNN控制提高了系统的鲁棒性和跟踪性,更加实用有效,具有一定的实用价值。
[1]叶云岳.直线电机原理与应用[M].北京:机械工业出版社,2000.
[2]王辉,马军,刘红霞.基于智能滑模观测器的PMLSM调速系统研究[J].电气传动,2014,44(6):54-57.
[3]陆华才,徐月同,杨伟民,等.永磁直线同步电机进给系统模糊PID控制[J].电工技术学报,2007,22(4):59-63.
[4]Lin F J,Shen P H,Yang S L,et al.Recurrent Radial Basis Function Network-based Fuzzy Neural Network Control for Permanent-magnet Linear Synchronous Motor Servo Drive[J].Magnetics,IEEE Transactions on,2006,42(11):3694-3705.
[5]Li Y,Chen Y,Zhou H.Control of Ironless Permanent Magnet Linear Synchronous Motor Using Fast Terminal Sliding Mode Control with Iterative Learning Control[C]//American Control Conference,ACC2009.IEEE,2009:5486-5491.
[6]Wang L,Chen J.Integrated Strategy of Permanent Magnet Linear Synchronous Motor Based on Sliding Mode Control and Repetitive Control[C]//Computer Science and Information Technology(ICCSIT),2010 3rd IEEE International Conference on.IEEE,2010,9:652-655.
[7]舒怀林.PID神经元网络及其控制系统[M].北京:国防工业出版社,2006.
Control for PMLSM Based on PIDNN
CAI Manjun,ZHAO Xiaodong,ZHAO Chengyuan
(Key Lab of Industrial Computer Control Engineering in Hebei Province,Yanshan University,Qinhuangdao066004,Hebei,China)
For permanent magnet linear synchronous motor as the actuator of the drive system being vulnerable to the influence of the periodic disturbance such as the end effect,etc,the PIDNN control methods based on PID neural network was proposed.PIDNN which had the function of proportion,integral and differential neurons,incorporated PID control law into the neural network.PIDNN effective inhibited end effect,thrust ripple,the cogging force and the friction disturbance to the system.Compared with the traditional PID control,Simulation experiments show that the PIDNN control improves the robustness and traceability of the system,and is the more practical and effective.
permanent magnet linear synchronous motor;proportional-integral-derivative neural network;neural network;disturbance rejection
TM359.4
A
10.19457/j.1001-2095.20161201
2015-11-25
修改稿日期:2016-07-26
国家自然科学基金(20577038);河北省科技计划项目(10213944)
蔡满军(1957-),男,博士,教授,Email:404926788@qq.com
