基于改进自适应算法APF直流侧稳压策略研究
2017-01-04夏伟红严正藩李志新张晓
夏伟红,严正藩,李志新,张晓
(中国矿业大学信息与电气工程学院,江苏 徐州 221008)
基于改进自适应算法APF直流侧稳压策略研究
夏伟红,严正藩,李志新,张晓
(中国矿业大学信息与电气工程学院,江苏 徐州 221008)
针对APF传统自适应谐波检测法的不足,提出一种改进自适应谐波检测法。该方法通过在传统自适应滤波器参考输入上乘以基波电流有效值信号,使得在权值更新过程中可减少迭代运算次数。在不影响检测精度情况下,快速地寻找到最优权值系数,加快了系统动态性能,很好地解决了收敛速度与稳态精度的矛盾。同时提出一种基于该方法的APF直流侧稳压控制策略。最后通过仿真和实验验证了该谐波检测法及直流侧电压控制策略的可行性和有效性。
有源电力滤波器;自适应谐波检测法;直流侧电压控制
随着电力电子设备以及非线性负载的大量应用,大量的谐波产生并注入到电网,因此电网中谐波污染问题变得日益严重。有源电力滤波器APF是一种动态抑制谐波和无功功率补偿的新型电力电子装置[1-2],而谐波检测的快速性和精确程度决定了APF的补偿性能。自适应谐波检测方法的算法简单,易于实现,对系统元件参数变化不敏感。因此近年来对自适应谐波检测的研究日益广泛和深入[3-6]。文献[7]给出了一种用于APF的自适应谐波电流检测方法,但是却没有给出相应的直流侧稳压策略。本文介绍了基于LMS算法的自适应谐波检测方法,在三相负载对称时,能够直接检测出基波电流。为了解决收敛性与精度相互矛盾的问题,对LMS谐波检测方法进行了改进,改进方法在不影响精度的情况下提高了收敛速度。同时提出了一种基于该方法的APF直流侧电压控制策略,保证了直流侧电压的稳定。
1 最小均方的自适应谐波检测
1.1 LMS谐波检测方法的基本原理
最小均方算法,即LMS(least mean square)是由Widrow和Hoff在20世纪60年代提出来的。该算法结构简单,可收敛,在实际中应用广泛。但是它存在收敛速度慢、有额外误差等问题。其基本思想是:输入信号包含期望输出信号,通过自适应滤波器可以让其输出接近期望输出信号,滤波器输出与期望信号之间有误差,误差通过反馈调整滤波器参数,使滤波器的输出逼近期望信号,当滤波器参数达到最优时,滤波器输出对期望信号的误差最小[8]。
自适应滤波器可以用于分离出谐波信号中的正弦信号。有不少学者研究基于自适应滤波器的谐波检测技术,即自适应谐波检测方法。对于APF来说,需要检测谐波电流,可以使用自适应谐波检测方法,原理图如图1所示。
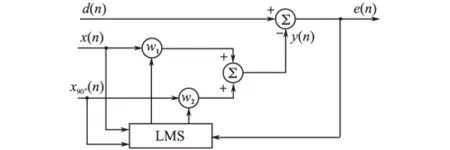
图1 LMS谐波检测原理图Fig.1 Schematic diagram of LMS harmonic detection
图1中,d(n)可以看成含有谐波电流的负载电流,是输入的参考信号,y(n)是自适应滤波器的输出信号,e(n)是误差信号。当自适应滤波器输出的信号y(n)逼近基波电流时,则e(n)就是需要检测的谐波电流。
输入的参考信号x(n)可以由电网电压锁相环产生,另外一个输入信号是x90°(n),x(n)与之相差90°,两者是互相正交的正余弦信号。基于LMS算法的自适应谐波检测方法可以通过下式实现:

式中:μ为步长。
当d(n)作为A相负载电流时,由自适应滤波器输出y(n)可以得到A相基波电流;同理,当d(n)作为B,C相负载电流时,自适应滤波器输出y(n)可以得到B,C相基波电流。求出三相基波电流就可以得到三相谐波电流。该方法实现原理简单,计算时间较长。
1.2 LMS谐波检测方法收敛性分析
为了使LMS算法收敛,步长必须满足下式:

LMS算法的总体平均误差为
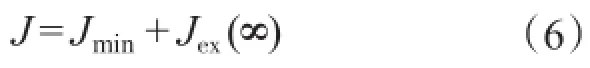
可以看出,LMS算法达不到最小总体平均误差的性能要求,存在1个误差,该值为
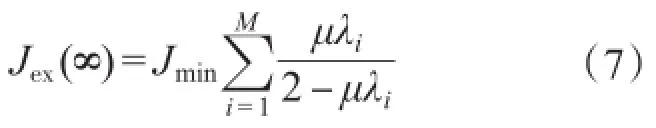
定义失调系数为

可以看出,失调系数反映了LMS算法收敛的性能。失调系数越小,LMS算法越接近最优滤波器性能;反之,失调系数越大,LMS算法的收敛结果与最优滤波器的性能差距越大。
1.3 步长对LMS谐波检测方法的影响
三相负载电流为

经过三相自适应滤波器,可以得到下式:

进而求得谐波电流,如下式:

三相电网电压的线电压为90 V,平波电抗器为0.2 mH,谐波源为不可控整流桥接纯阻性负载。在0.3 s时,负载由8 Ω突变到4 Ω,A相负载电流如图2所示。
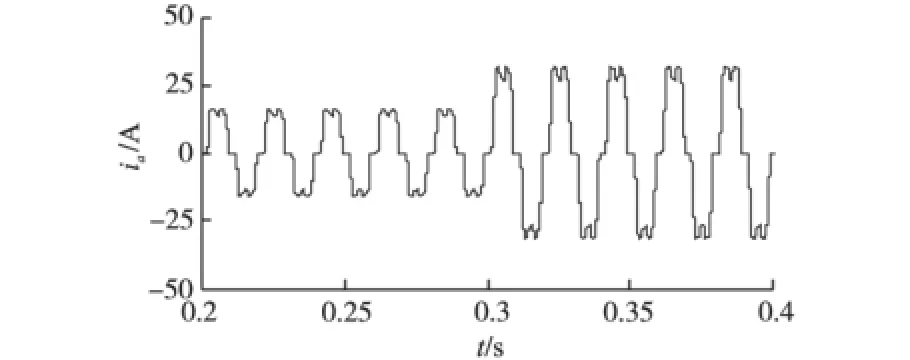
图2A相负载电流Fig.2Aphase load current
对A相负载电流进行谐波分析,负载为8 Ω时,基波电流的幅值为16.49 A,谐波畸变率为27.90%;负载为4 Ω时,基波电流的幅值为32.39A,谐波畸变率为26.78%。
由LMS谐波检测方法得到的A相基波电流如图3所示。其中步长μ=0.01。
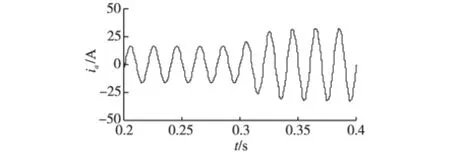
图3 步长为0.01时,A相基波电流Fig.3Aphase fundamental current under step is 0.01
由LMS谐波检测方法得到的A相基波电流如图4所示。其中步长μ=0.008。

图4 步长为0.008时,A相基波电流Fig.4Aphase fundamental current under step is 0.008
对LMS谐波检测算法得到的基波电流进行谐波分析。在步长为0.01时,负载为8 Ω,基波电流的幅值为16.48 A,谐波畸变率为2.01%,负载为4 Ω,基波电流的幅值为32.82 A,谐波畸变率为2.04%;在步长为0.008时,负载为8 Ω,基波电流的幅值为16.47 A,谐波畸变率为1.61%,负载为4 Ω,基波电流的幅值为32.80 A,谐波畸变率为1.59%。可以看出,步长为0.01与步长为0.008相比较,LMS谐波检测方法得到的基波电流存在较大的畸变率。但是,在负载突变时,步长为0.01与步长为0.008相比较,检测得到的基波电流稳定得较快。
也就是说LMS谐波检测方法的步长选择很重要,步长影响基波的检测精度,步长越小,检测的基波电流误差越小。但是当环境发生变化时,即负载发生突变时,步长越小,收敛速度越慢,检测得到的基波电流稳定得越慢。
1.4 改进的LMS谐波检测方法
针对步长小时,收敛速度慢的问题,对LMS谐波检测方法进行改进。改进后的LMS谐波检测原理图如图5所示。
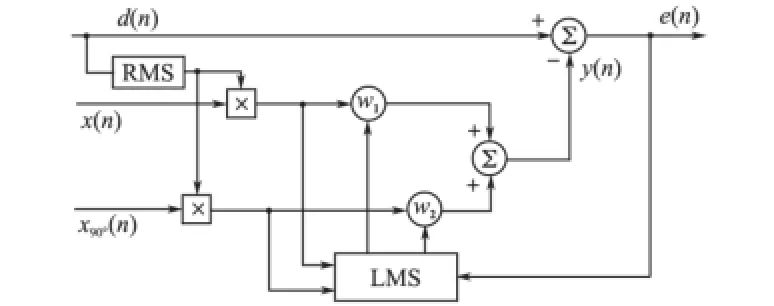
图5 改进LMS谐波检测原理图Fig.5 Schematic diagram of improved LMS harmonic detection
由文献[9]可知,
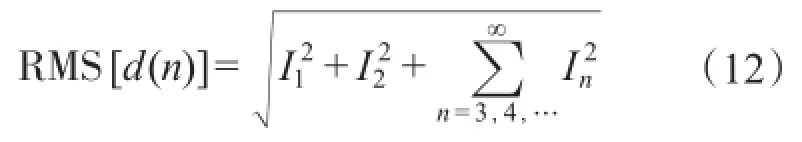
式中:RMS[d(n)]为d(n)的有效值。
在稳态时,可通过式(5)计算出负载电流的有效值;考虑到负载电流中基波电流的含量远远大于其谐波含量,因此,可以利用所得的负载电流有效值RMS[d(n)]来替代负载基波电流有效值。
以A相为例,由图5可知,将A相负载电流d(n)的有效值作为系数叠加到两相参考上,并与各相的权值相乘得到自适应滤波器的输出y(n),数学表达式如下式:

改进后的LMS谐波检测方法得到的A相基波电流如图6所示。步长为μ=0.000 008。

图6 步长为0.000 008时,A相基波电流Fig.6Aphase fundamental current under step is 0.000 008
改进后的LMS谐波检测算法,步长为0.000008时,负载为8 Ω,基波电流的幅值为16.32 A,谐波畸变率为0.43%;负载为4 Ω,基波电流的幅值为32.42 A,谐波畸变率为1.66%;可以看出得到的基波电流畸变率明显要小于未改进的LMS谐波检测方法。而且在负载发生突变时,改进后的LMS谐波检测方法收敛速度要快于未改进的LMS谐波检测方法,基波电流稳定速度变快。
通过这种方式,与未改进的LMS谐波检测算法相比,在系统运行的初始阶段,A相负载电流d(n)与自适应滤波器输出y(n)差值较小,作差得到的谐波电流信号e(n)与需要检测谐波电流相对较接近,因此在权值更新的过程中可减少迭代运算过程,减少计算量,在不影响检测精度情况下,以较少的时间寻找到最优的权值系数,大大加快了系统的动态性能,在后面的仿真及实验中验证了该算法的正确性。
2 直流侧稳压控制策略
本文提出了一种适合于改进自适应谐波检测算法的APF直流侧电压控制策略。分析可知,流经APF的电流主要包含2部分:第1部分为需补偿的谐波指令电流;第2部分为直流侧稳压指令电流。
由文献[10]理论分析可知,三相电路的瞬时有功功率与电路中有功功率相等,这反映APF直流侧与交流侧存在有功能量交换。然而瞬时无功功率为零,这说明电源并不向负载提供无功功率,而无功功率是在三相之间流动,反映APF直流侧与交流侧不存在无功能量交换。所以,直流侧稳压电流分量是由三相共同产生且相位与基波电压相同的有功电流。因此将直流侧给定值与实际值作差经PI调节器后得到直流稳压分量的幅值,再与锁相环(PLL)得到三相电压的基波相位相乘,得到的结果即为直流侧稳压所需要的调制信号,将该信号平均分配到三相谐波电流中,即可使直流侧与交流侧交换能量,从而达到直流侧稳压的作用。以A相为例,直流侧电压控制框图见图7。同理可得B,C两相的情况。

图7 直流侧电压控制框图Fig.7 The block diagram of DC side voltage control
3 仿真分析
利用Matlab中Simulink搭建该APF仿真模型,设置系统的仿真参数如下:网侧线电压有效值90 V,非线性负载为三相不控整流桥带8 Ω电阻,非线性负载连接电感0.45 mH,直流侧电容2 200 μF,交流侧电感1.5 mH,APF直流侧电压参考值为180 V,主回路采用SVPWM调制算法控制,开关频率为12.5 kHz,LMS算法仿真步长取为0.000 008。仿真波形如图8所示。

图8 仿真波形Fig.8 Waveforms of the simulation
由图8看出,基于该自适应谐波检测的APF补偿效果良好,对A相电流进行FFT分析,可知谐波电流明显下降,总谐波畸变率由22.5%降为3.81%。且在负载由8 Ω突变到4 Ω时,系统仍然具有快速的响应性能,同时直流侧也具有较好的稳压效果。
4 实验验证
实验验证是在两电平APF实验平台上进行的。该平台主要分为主电路与控制回路两部分。主电路图如图9所示。实验参数与仿真参数一致。

图9 两电平实验平台主电路图Fig.9 Main circuit of two-level experimental platform
实验波形如图10所示。由图10可看出三相网侧电流在补偿后接近于正弦,对补偿后的三相电网电流谐波分析可看出,三相电流谐波畸变率由22.5%降为4.8%左右,补偿效果良好,同时直流侧电压基本上稳定在180V,具有较好的稳压效果。

图10 实验波形Fig.10 Waveforms of the experiment
5 结论
详细介绍了基于最小均方的自适应谐波检测方法,并在该基础上进行改进得到新型谐波检测方法,该方法收敛速度以及基波电流稳定速度明显加快,且不受系统参数改变的影响,可直接应用到单相、三相系统中。同时提出了一种基于该方法的APF直流侧电压控制策略,该方法具有实现简单,计算量小等优点。最后通过仿真和实验证明上述理论的正确性与可行性。
[1]王兆安,杨君,刘进军.谐波抑制与无功功率补偿[M].北京:机械工业出版社,2006.
[2]王建元,张国富.有源电力滤波器的控制策略综述[J].电气传动,2007,37(6):6-11.
[3]芮颖,牟龙华.基于自适应滤波算法的谐波仿真分析[J].电力系统及其自动化学报,2009,21(4):76-81.
[4]何娜,黄丽娜,武健,等.一种新型快速自适应谐波检测算法[J].中国电机工程学报,2008,28(22):124-129.
[5]盘宏斌,罗安,唐杰,等.一种改进的基于最小二乘法的自适应谐波检测方法[J].中国电机工程学报,2008,28(13):144-151.
[6]张俊敏,田微.基于瞬时无功功率理论谐波检测方法的研究[J].电力系统保护与控制,2008,36(18):33-36.
[7]李乔,吴捷.自适应谐波电流检测方法用于有源电力滤波器的仿真研究[J].电工技术学报.2004,19(12):86-90.
[8]张旭东,崔晓伟,王希勤.数字信号分析与处理[M].北京:清华大学出版社,2014.
[9]鞠建永,陈敏.模块化并联有源电力滤波器[J].电机与控制学报,2008,12(1):20-26,33.
[10]高大威.电力系统谐波、无功和负序电流综合补偿的研究[D].保定:华北电力大学,2001.
修改稿日期:2016-06-10

图11 一相1.25 kW、一相空载时的直流中点电压和逆变输出电流波形Fig.11 DC link midpoint voltage and inverter output current waveforms with 1-phase no load and 1-phase 1.25 kW
4 结论
本文对用于北美家庭两相三线电网电压的并网光伏逆变器的拓扑结构、传递函数、控制方法进行了研究,提出了叠加负载电流前馈的直流电压外环、逆变出口电流内环的双环控制方法,既可实现直流电压的稳定也能对不对称负载电流进行跟踪,而后对逆变器直流中点电压的控制进行了分析。最后,通过仿真与实验波形验证了该控制方法的有效性与可行性。
参考文献
[1]张兴,邵章平,王付胜,等.非隔离型三相三电平光伏逆变器的共模电流抑制[J].中国电机工程学报,2013,33(3):29-36.
[2]董钺,芮春保,李钊,等.采用比例谐振控制的三相四桥臂并网逆变器的研究[J].电气传动,2014,44(4):42-45.
[3]Yi Tang,Poh Chiang Loh,Wang Peng,et al.Exploring Inherent Damping Characteristic of LCL Filters for Three-phase Grid Connected Voltage Source Inverters[J].In IEEE Transactions on Power Electronics,2012,27(3):1433-1443.
[4]姜卫东,杜少武,史晓锋,等.中点钳位型三电平逆变器空间矢量与虚拟空间矢量的混合调制方法[J].中国电机工程学报,2009,29(18):47-53.
[5]姜卫东,王群京,史晓锋,等.中点钳位型三电平逆变器在空间矢量调制时中点电位的低频振荡[J].中国电机工程学报,2009,29(3):49-55.
[6]宋文祥,陈国呈,束满堂,等.中点钳位式三电平逆变器空间矢量调制及其中点控制研究[J].中国电机工程学报,2006,26(5):105-109.
收稿日期:2015-11-13
修改稿日期:2016-07-14
Research on DC Voltage Balance Control Strategy of APF Based on Improved Adaptive Algorithm
XIA Weihong,YAN Zhengfan,LI Zhixin,ZHANG Xiao(School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou221008,Jiangsu,China)
Aiming at the shortcomings of the traditional adaptive harmonic detection algorithm of APF,a improved adaptive harmonic detection algorithm was proposed.The method was based on that the reference input of traditional adaptive filter multipied by the effective value of the fundamental current,the number of iterations could be reduced in the process of updating the weights.In the case of not affecting the accuracy of detection,the optimal weight coefficient could be found quickly,and the dynamic performance of the system could be accelerated.It was a good solution to the contradiction between convergence speed and steady state accuracy.At the same time,a new DC voltage control strategy of APF was proposed,which could guarantee the stability of the DC voltage.Finally,the feasibility and effectiveness of the proposed harmonic detection and the DC voltage control strategy are verified by simulation and experiment.
active power filter;adaptive harmonic detection algorithm;DC side voltage control
TM76
A
10.19457/j.1001-2095.20161210
2015-10-14
夏伟红(1993-),男,硕士研究生,Email:xiawhcumt@163.com
