图论在教师排课管理中应用
2017-01-03李芳
李芳
【摘要】学校的排课管理作为教务系统中最为极为重要的一个环节之一,如若排课不恰当会造成多种冲突情况发生,如实验教室的使用发生冲突、上课时间上的冲突以及教师授课的冲突,然而这些问题都会一定程度上对教学效率造成不利影响。通过图论的相关理论能够有效的避免这些冲突的产生,从而确保学生能够正常上课,保障学习效率。
【关键词】图论教法 教师排课管理 应用分析
【中图分类号】G715 【文献标识码】A 【文章编号】2095-3089(2016)11-0154-01
一、引言
课表的安排管理问题是学校教学中时间以及地点安排问题,这一问题的解决需要学校的相关教务管理人员花费较大强度的脑力与长时间的安排,是教务系统的核心工作。学生的课表安排需要结合许多因素,如:教室、班级以及上课时间等。因为要将多种因素结合考虑,所以通常情况下相关负责人员只能够手工安排课表。而这种方式在信息技术不断普及的状态下,效率显得十分低下。文章从图论的角度来对课表问题进行分析,提出最佳排课模型以满足实际需要。
二、排课的由来
排课是学校教学管理中十分重要而又具有较大难度的一项任务,它指的是给学校设立的老师教学课程的安排提供合适的时间,进而让各个老师的教学时间不会发生冲突,让老师的教学工作顺利开展。在老师的排课管理中,其中主要工作就是合理安排各项资源,例如:教学地点、学科以及时间等方面。通常情况下,是以一个循环周期的方法来适当的调配,让各项资源不会冲突。换种说法,排课是为了让老师与学生的时间以及上课地点进行统一。所以,课表则是排课工作的最终体现,课表算法是为了合理的安排老师与学生时间以及上课地点的统一。
三、传统排课模型算法的不足
为防止老师与学生时间以及上课地点发生冲突,则出现了排课算法。现今大部分的排课算法都是模拟手动排课的操作方法,利用计算机进行编排,老师的排课先按以往的编排习惯来调配老师与学生的时间以及上课地点,等到有问题出现时再进行相应的调控,但新的调整又有较大可能引发新的问题出现,这就无法很好的解决问题,并且没有效率。除此之外,这类算法还无法确保预算出的结论较优。
四、图论在教师排课管理中的应用
在编排课表的过程中,其主要目的是合理的安排老师与学生时间以及上课地点的统一。在这当中,有过多的可能性。因此可以把模型划分为两部分来考虑:一是老师与学生时间上的安排,二是老师与学生上课地点的安排,在进行这两种安排的过程中都可以运用图论方法来运作解决。
1.教师排课管理中时间的安排
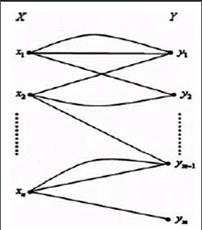
教师排课管理中时间的安排其实质是指让教师在指定的时间内去给某个班级上课。在这当中,需要满足以下几个要求:首先,在同一个时间范围内教师只可以给一个班级上课;其次,不同班级在同一时间也只能有一个老师教课。运用图论方法来解决这一问题,如:有N个老师,分别是X1....XN,另外有M个班级,分别是Y1....YN,其中某个老师要教某个班级就要将这两者用线连接起来,若是一个星期之内某个老师给某个班级上了两次课,则用两条线相连,依次增加。使用二部图Z表示,让Z=(W,X,Y),其中W指的是连接老师与班级之间的线。具体如图一所示:
图一
众所周知,同一个顶点的边是相邻边。对每条边用不同颜色上色,一种颜色指代一段时间,拿大学为例,大学课程一般为两课时一节课,一天四节,一星期五天,因此在教师排课管理中边色数应为二十,指代的是二十段时间,一样的颜色指代的是一个时间段是由于相同时间当中每个老师只可以去一个班级教课,不同班级在同一时间也只能有一个老师教课。相邻边指代的是老师或学生是相同的,不能安排在同一时间段内上课,这就要求相邻边不可以使用相同颜色标明。
2.教师排课管理中上课地点的安排
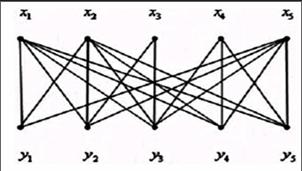
教师排课管理中上课地点的安排其实质是让某个班级在一个时间段内到指定的上课地点上课,在这当中,需要满足以下几个要求:首先,在同一个时间范围内教师只可以给一个班级上课;其次,不同班级在同一时间也只能有一个老师教课。最后,要保证班级的总人数要比教师的容纳量小,确保学生有位置坐。但又不能让教师太大,否则会影响上课效果。运用图论方法来解决这一问题,如:在指定的时间段内,有五个班级X1至X5要安排不同教师上课,这时刚好又有五个教室Y1至Y5可以用,两者之间的关系如图二:
图二
根据不同教室的使用来赋值,设立的权限可以从以下数据看出:
W
5 5 5 2 1
2 4 4 1 2
0 2 1 0 0
0 0 3 3 3
1 4 4 1 2
其中这些数据中一个数表示的是不同班级分配到不同教室的适合程度,数字越大表示适合程度越高,就可以先行考虑。不过不管如此,到最后都要确保五个班级都要有适合的教室上课。
五、结语
将本文所述的两类方法结合,就能构建一张完整的课表,这样就能保证老师与学生时间以及上课地点能够保证同步。其中运用的实际方法就是图论法,图论运用至教师排课管理中,有助于解决以往排课过程中的困难,打破传统排课方法的局限性,进而防止老师与学生的上课时间发生冲撞,提高教学效率。
参考文献:
[1]吴丈虎,王建德.图论的算法与程序设计[J].北京:清华大学出版社,2013.06.(05):39-43.
[2]王凤,林杰.高校排课问题的图论模型及算法[J].计算机工程与应用,2014.11.(13):373-375.
[3]程泉,朱大铭.用图的着色方法求解考试时间安排问题[J].计算机应用,2015.04.(21):117-119.
