几何类新知课“全等三角形的概念及性质”教法例说

匡金嫦+马琳

一、教材分析

（一）地位和作用

本课为湘教版八年级上册第二章第五节《全等三角形》第一课时所教授的内容，在三角形的相关知识中具有重要的地位和作用：它是探究三角形全等条件的基础，是证明线段相等、角相等的重要依据，也是渗透对应思想的重要一课，同时为学生之后学习三角形相似奠定基础，而学生之前已经学习了三角形和图形平移、旋转、翻折的基础知识，因此，该课在有关三角形的知识结构中具有承上启下的作用.

（二）教学目标

1.知识与技能：（1）理解全等图形、全等三角形的概念及全等三角形的表示方法；（2）能熟练找出全等三角形的对应顶点、对应边和对应角；（3）掌握全等三角形的对应边、对应角相等的性质，并能运用该性质进行简单的几何推理.

2.过程与方法：（1）让学生经历观察、猜想、合情说理、归纳总结的过程，获取全等三角形的基础知识；（2）让学生观察、分析图形变换的规律，寻找全等三角形经过图形变换后的对应关系，提高学生的识图能力和简单的几何推理能力，积累数学活动经验.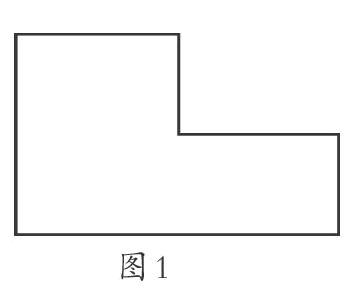

3.情感态度与价值观：（1）通过引导学生观察图形的平移、旋转、翻折过程，培养其运动观点；（2）通过引导学生观察图形变换及亲自动手操作，发展其空间观念，培养其几何直观；（3）通过组织学生经历观察、分析、交流、讨论的过程，培养其独立思考和团队合作的意识与能力.

（三）教学重难点

1.重点：探究全等三角形的性质，准确辨认全等三角形的对应元素.

2.难点：运用全等三角形的性质进行简单的推理和计算.

二、教学设计

（一）教法选择

本课属于几何类新知课，教法上我们拟采用新知课的四环节教学模式进行设计：第一环节“问题导入”，旨在设疑激趣；第二环节“新知探究”，重点是合情归纳；第三环节“变式应用”，重点是图形变换；第四环节“总结升华”，重点是应用思维导图沟通新旧知识间的联系.

（二）教学内容的考量因素

1.基础性.学习三角形全等，是之后学习三角形相似的基础，因此，在课中渗透对应思想至关重要.

2.关联性.全等三角形与图形变换息息相关，图形变换就是一种全等变换，所以在运用全等三角形解决问题时，常常可以通过图形变换来寻找或构造全等三角形.

3.拓展性.全等三角形是几何图形由线、角的开放图形到封闭图形的过渡，研究范围可拓展到对图形形状、周长、面积的多元探究，因此在教学素材的选取上，我们拟选择平移、旋转、翻折三种图形变换作为变式教学的载体，将全等三角形的概念和性质融合在具体的问题中，通过问题解决培养学生的识图能力和计算说理能力，进而突破教学的重、难点.当然，对于本文所呈现的教学设计，我们还可以根据学情的不同做适当的删减.若学生基础好，整体水平高，可选择梯度大的问题进行教学；若学生基础薄弱，整体水平较低，可选择坡度缓的问题进行教学.变式教学的宗旨是更精确地因材施教，让不同层次的学生都能得到相应的发展.

（三）教学过程

1.问题导入：设疑激趣，操作导入

在“问题导入”环节，让学生观察、猜测老师手中的纸片有几张（看似只有一张，但又似乎不止一张；图片形状如图1所示），使学生的直觉与教师的提问暗示产生冲突，在这似是而非的情境中，学生的探究兴趣被激发，而全等图形“完全重合”的概念已巧妙地隐含在这个猜测游戏中.

问题1：猜猜老师手中的纸片有几张？

2.新知探究：合情说理探究法

在“新知探究”环节设计两个小问.第一小问引导学生从整体角度观察全等图形与全等三角形的特点，使之从中发现两组图形“完全重合”的共性；第二小问引导学生从微观元素观察全等三角形的对应点、对应边、对应角的关系，进而运用“合情说理”进行新知归纳.

问题2：（1）观察老师手中的两组图形（见图2、图3），说说它们有什么共同特点？（2）若老师将图3中的两张图片重叠在一起，请观察这两个三角形，说说它们有哪些对应关系？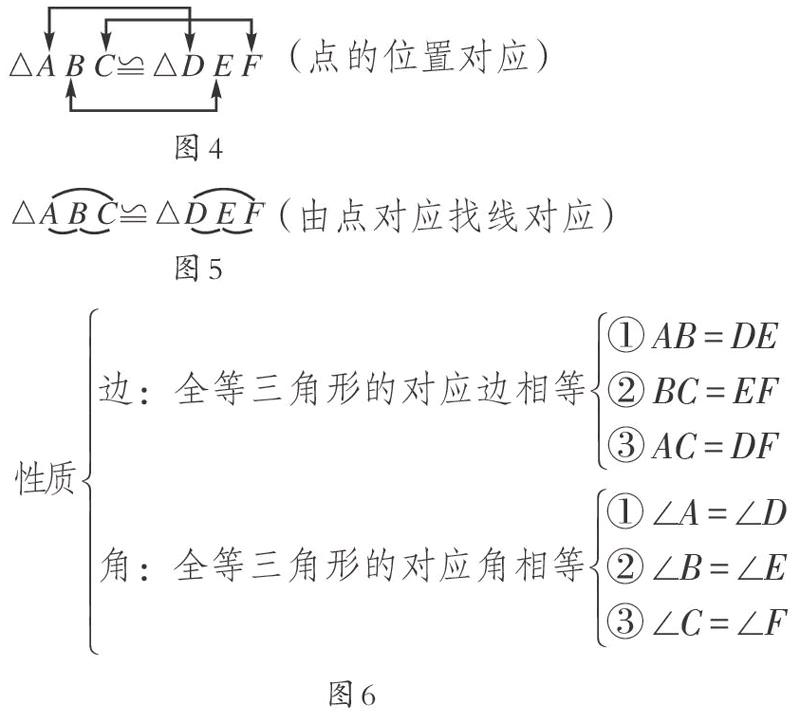

★引导学生归纳全等三角形的概念及性质.

（1）全等图形定义.能够完全重合的两个图形叫做全等图形.

（2）全等三角形的概念及性质.定义：能够完全重合的两个三角形叫做全等三角形.表示：用符号“”连结，如△ABC△DEF，读作“△ABC全等于△DEF”.点的对应与线的对应分别如图4、图5.全等三角形的性质如图6.

3.变式应用：几何变式中的“图形变换”变式

在这个环节，共设计四个问题，从问题3到问题6.

问题3安排一组根据图形变换设计的变式图，由平移（沿BC边平移，点B的对应点E分别在BC边上、在BC的顶点C处、在BC的延长线上，见图7、图8、图9）→旋转（绕△ABC的顶点A旋转，旋转角分别小于∠BAC、等于∠BAC、大于∠BAC，见图10、图11、图12）→翻折（沿BC边翻折，沿过点B的任意一条直线如BF、BD翻折，分别见图13、图14、图15）；

问题4选取平移变换所得的图7进行问题设计，设计思路是由找对应边、对应角→已知一个角求对应角→已知两个角求其余角→已知一条边求对应边→用字母变式线段的长度（由特殊到一般）→找与BE（平移距离）相等的线段（问题由封闭到开放）；

问题5选取旋转变换所得的图10进行问题设计，设计思路是由找对应边、对应角→已知一个角求角→已知两个角求角→找与∠1（旋转角）相等的角；

问题6选取轴对称变换所得的图13进行问题设计，设计思路是由找对应相等的线段→找等腰三角形→判定线的位置关系→已知垂线段求面积问题，问题设计由浅入深、层次推进.

设计以上4个问题，旨在引导学生通过观察图形变换，培养识图能力，进一步探究图形在变换过程中蕴含的变化规律和数量关系.

问题3：请同学们运用图形的平移、旋转、翻折规律，分析下列图形分别是经过了怎样的变换得到的.

问题4：如图7，将与△重合的△沿边向右平移至如图所示的位置，指出图中的对应边、对应角.

变式1：若∠A=100°，则∠D=________.

变式2：若∠A=100°，∠B=40°，你能求出图中哪些角？

变式3：若AB=5cm，则DE=_______.

变式4：若BC=acm，将△DEF由点B出发，沿BC平移bcm，你能用a、b的代数式表示哪些线段长度？

变式5：连接AD，图中与BE相等的线段有_______.

问题5：如图10，将与△重合的△绕点旋转至如图所示的位置，指出图中的对应边、对应角.

变式1：若∠B=50°，你能求出哪个角，它的值是多少？_______.

变式2：若∠B=50°，∠C=30°，你能求出图中的哪些角？

变式3：图中与∠1相等的角是_______.

问题6：将与△重合的△沿翻折至如图13所示的位置，并连结，请找出图中对应相等的线段.

变式1：请写出图中所有的等腰三角形.

变式2：试判定AD与BC的位置关系，并说明理由.

变式3：若OA=2cm，BC=5cm，你能求出哪些量？

★经过以上变式应用教学，可引导学生归纳全等三角形性质的以下应用.

（1）全等变换.平移、旋转、轴对称都是全等变换.

（2）对应关系.图形位置：通过图形形状确定对应关系；符号位置：通过字母位置确定对应关系.

（3）数量和位置.平移：对应点的连线相等且平行（或共线）；对应边相等且平行（或共线）；对应角相等.旋转：对应边相等；对应角相等；对应边的夹角等于旋转角.翻折：对应点的连线被对称轴垂直平分；对应边相等；对应角相等.

4.总结升华：思维导图归纳法

在这个环节，用三个小问引导学生回顾本节课的学习内容，沟通新旧知识间的联系，强化图形变换在全等三角形中的应用，在图形变换变式应用中掌握平移、旋转、翻折的特征.

问题7：通过本节课的学习，你掌握了哪些新的知识？这些新知与哪些旧知之间有紧密联系？通过问题解决，你从中收获了什么？

在本环节，我们主要想运用思维导图归纳法（见图16），帮助学生整理整节课的内容框架，归纳出有关线段中隐含的数量与位置关系以及有关角中隐含的数量关系，再以此为基础去研究图形形状和图形面积等问题.

（责编 白聪敏）