代数类新知课“平方差公式”四环节教学模式例析
2017-01-03涂爱玲梁艳云
涂爱玲+梁艳云
“平方差公式”属于代数类新知课中的公式课,运用四环节教学模式进行问题设计时,我们重点分析以下两个因素:一是作为客体的教学内容,主要从结构特征、模型思想、符号意识、教材地位四个方面进行思考;二是作为主体的学生,主要考虑学生的年龄特点、思维品质和认知基础.权衡以上两个因素的具体情况,我们在采用变式教学的主线设计时,将情境主线“断案高手→说理大师→变式赢家→归纳之王”隐藏在四个教学环节之中,使情境主线与教学环节交融互动,一路精彩生成.
第一环节:问题导入之“故事导入”
根据初一年级学生的心理特点和教学内容的结构特点,在本环节,我们决定用趣味“案情”导入新课,创设了一个发生在“狼大和羊二”之间的土地租赁事件,以激发学生的探究欲望和学习情趣,让学生跃跃欲试争当“断案高手”,同时暗含“知识就是力量”、用知识帮助弱小的价值观引导.
[片段实录]
师:欢迎来到变式大课堂!今天我们要从一个小故事开始——这是一个发生在地主狼大和佃农羊二之间的土地租赁事件.(课件出示故事和“问题1”)
一天,狼大对羊二说:羊二啊!我家土地重新规划了,原来租给你的那块正方形土地,我把它向东增加了3米,向北减少了3米,变成了一块长方形,反正面积没变,你就种这块新地吧!不过,估计你也听不懂.我就画两幅图给你看看吧!(见图1、图2两个示意图)
羊二看了,连忙对狼大说道:老爷,我听您的!
问题1:羊二吃亏了吗?
师:羊二吃亏了吗?
生:(异口同声)吃亏了!
师:谁能为这个案子当个“断案高手”吗?(学生纷纷高举着手)
在本环节教学中,我们用故事中的问题情境导入新课,自然地将实际问题抽象为数学问题;运用数形结合思想,将土地面积问题转化为几何图形问题,突出了数学直观,生动易懂,也为接下来的新知探究提供了方法和思路.
第二环节:新知探究之“数形结合探究”
教师采用数形结合思想,引导学生进行新知探究,并为此设计了三个逐层递进的变式题.
[片段实录]
师:怎么判断羊二是否吃亏呢?(相对于问题1的“变式题1”)
生1:计算S1与S2,比较它们的大小.S1=a2,S2=(a+3)(a-3)=a2-3a+3a-32=a2+(-3+3)a-9=a2-9.
师:若向东增加5米,向北减少5米呢?(“变式题2”)
生1:还是一样地计算、比较,羊二还是吃亏.
师:若向东增加b米,向北减少b米呢?(“变式题3”)
生1:也是一样的.
师:同学们同意吗?
生:(大声,整齐)同意.
师:我们是不是可以借鉴刚才这位同学的方法推导一下,这样才好推广吧?(师课件出示图3示意图,并带领学生进行计算)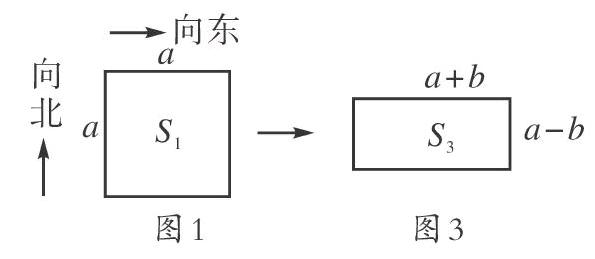
S3=(a+b)(a-b)=a2-ab+ab-b2=a2+(-b+b)a-b2=a2-b2
师:我们通过计算,进一步验证了一般情况下,正方形边长一增一减会导致面积减少.可羊二没文化,他不会算,我们有没有更直观的方法,让羊二一看就明白呢?
生2:我们可以先在这块地的南部向北裁掉一个如图4所示的矩形,再向东增加一个如图5所示的矩形,由图我们很容易看出,原来的正方形面积少了一个如图6所示、边长为3的小正方形.同样的,若正方形边长向东增加b向北减少b,则面积减少b2.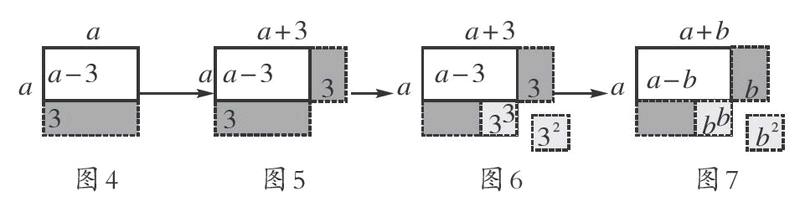
老师竖起大拇指;其他同学对这一直观的方法非常佩服,报以热烈掌声.
师:我们从两个角度,一是从代数的角度进行了精准的计算,二是从几何的角度进行了直观的验证,都得出了(a+b)(a-b)=a2-b2这个恒等式.通常二项式乘二项式展开以后得四项,为什么这组二项式相乘展开以后才有两项呢?
生:(齐声)因为有两项是同类项,互相抵消掉了.
师:为什么能互相抵消呢?
生:(齐声)因为b与-b互为相反数.
师:那么这个等式的左右两边究竟有哪些特点呢?
生3:等式左边是两个二项式的乘积,且只有a、b两项,一个二项式是a+b,一个二项式是a-b,等式右边是a与b的平方差.
师:看来同学们都是“说理大师”啊.(生笑)
在这个教学环节,教师通过激励学生对“案情”进行推理、演算,引导学生从代数和几何两个角度来验证自己的结论,再进一步追问,启发学生对平方差公式的结构进行深层次剖析,使学生得以自主发现并归纳出平方差公式这个新的知识点.
第三环节:变式应用之“代数变式的主线设计”
从一道基本题切入,运用代数的“式子变式”沿“系数变→符号变→位置变→指数变→因式变→项数变”的思维路径进行变式设计,使问题设计由浅入深、层层推进.根据平方差公式的结构特点,引导学生对公式进行多角度的变式应用,可以使学生对平方差公式有更深的理解,有利于培养学生思维的灵活性和深刻性.
[片段实录]
师:我们已经认识了平方差公式,接下来我们将——
生:(齐声)应用.
师:(调侃)看来你们很了解呀!(生喜形于色)
课件出示平方差公式基本模型及基本题“问题2”.
平方差公式:(a+b)(a-b)=a2-b2
问题2:计算(+3)(-3)
师:问题2是否符合平方差公式的结构特点?若符合,公式中的a、b分别是什么?
生4:完全符合平方差公式的结构特点,公式中的a就是a,公式中的b就是3.
师依次出示以下变式题组中的每一个变式,要求学生一题一题地说一说:该题是否符合平方差公式的结构特点?若符合,公式中的a、b分别是什么?比较这一题与上一题发生了什么变化?依次问答毕,师板写变式题组的变式过程如下.
问题2:(a+3)(a-3)
系数变↓
变式1:(2a+3)(2a-3)
符号变↓
变式2:(-2a+3)(-2a-3)
位置变↓
变式3:(3-2a)(-2a-3)
指数变↓
变式4:(3-4a2)(-4a2-3)
因式变↓
变式5:(3b-4a2)(-4a2-3b)
项数变↓(相对于公式而言)
变式6:(a+b+c)(a-b+c)
师:结合以上变式题组,你认为平方差公式中的a、b可以表示什么?
生5:公式中的a、b可以表示数,可以表示单独的一个字母,也就是说既可以表示一个单项式,也可以表示一个多项式.
师:你的理解非常到位!公式中的a、b可以代表我们已经学过的任意一个整式,当然还可以推广到代数式.
师:仔细观察以上变式题组,你对代数中的变式方法有了哪些了解?
生6:我们可以从系数、指数、项数、因式、符号、位置等角度进行变式,其实就是抓住整式中的基本元素进行变式.
师:你的理解太深刻了,你能很好地抓住问题的本质,问题虽然可以千变万化,但都遵循一定的变化规律.我们不妨把以上变式方法叫做变式策略.你可以说是我们这节课的“变式大赢家”!(生喜形于色)
引导学生对变式题组中的变式题进行解答,可以使学生逐步学会分析式子结构,认清公式中的a和b分别代表什么,能够准确运用公式进行计算,同时了解代数中变式的基本策略,认清变化的规律,抓住不变的本质.
第四环节:总结升华之“思维导图归纳法”
用问题3的三个小问为思维支架,引导学生对本节课所学内容进行梳理,帮助学生自主建构知识体系,厘清知识之间的联系,并在锻炼解题的过程中训练学生的语言表达能力.最后引导学生运用“思维导图”归纳本课的知识、方法和蕴含在其中的数学思想,以此培养学生的综合素质.
[片段实录]
师:同学们的表现非常出色!那么谁又能成为本节课的“归纳之王”呢?(课件出示“问题3”)
问题3:(1)对于平方差公式,你有哪些认识?(2)本节课你印象最深的是什么?(3)你还存在哪些疑惑?
生7:我认为平方差公式的结构很特别.它是a、b两项的和与a、b这两项的差的乘积,结果等于a、b的平方之差,而且是符号相同的项a的平方减去符号相反的项b的平方,前后不能颠倒.
生8:本节课我学到的知识概括起来有两点.第一点,运用平方差公式一定要准确地找出公式中的a和b;第二,对于因式中出现三个项或以上,一定要观察各项的符号,再结合,构造出平方差公式的结构.
两名学生对平方差公式的应用做出了非常全面的概括,这让在场的老师和同学们都听呆了,继而爆发出雷鸣般的掌声.
师:好,她们都是“归纳之王”!
接下来,师课件出示本课知识思维导图(见图8).
教师从学生的角度,启发他们思考对平方差公式有怎样的认识,鼓励他们说出这节课中印象最深的是什么,激励他们反思心中的疑惑,独立思考,小组讨论,班级交流,充分尊重学生在学习中的主体地位.
本节课将问题主线和情境主线相互交融,知、情、意有机结合.问题主线从数学学科的特点出发,设计出了一条条理清晰、逻辑严谨的问题链,问题设计抓住了本节课的核心知识即平方差公式,从平方差公式的发生、发现、发展、应用及拓展几个层次依次设计出了一个个问题串,将本课的核心能力、发散思维能力、创造能力等渗透其中,体现了数学的理性美.情境主线主要从情感态度价值观角度出发,将“授人以鱼不如授人以渔”进化为“授人以渔不如授人以欲”,从问题情境“羊二吃亏了吗?”开始,层层设疑、层层追问、步步为营,带领学生逐渐展开本课的“探索发现与应用之旅”,并运用心理暗示将学生置身于“断案高手”“说理大师”“变式赢家”“归纳之王”的角色中,引领着学生自主解决了一个个预先设定好的情境任务,让学生在挑战自我的过程中实现了自身价值,这也正是执教者想通过情境主线来开启和激励学生自主探索、自主发现的教学艺术所在.
(责编 白聪敏)
