量子粒子群算法在配电网多时段动态重构中的应用

王 伟， 谭阳红

(湖南大学 电气与信息工程学院， 湖南 长沙 410082)



量子粒子群算法在配电网多时段动态重构中的应用

王 伟， 谭阳红*

(湖南大学 电气与信息工程学院， 湖南 长沙 410082)

针对配电网负荷随时间不断变化的情况，提出了一种配电网多时段动态重构新方法。该方法以配电网有功损耗最少和开关操作次数最少为综合优化目标函数，构建多目标动态重构模型，采用开关环路矩阵与节点分层判别方法快速消除无效解，采用整数型环网编码策略大幅降低变量维数。针对该复杂模型的求解，提出了一种更适合求解配电网动态重构的整数编码型量子粒子群优化算法，对其进行有功网损最少化的时段初步划分，并在初步划分的基础上进行开关操作次数最少化的时段二次优化，进而确定最优重构方案。通过对IEEE33节点系统进行动态重构，验证结果表明本文所提方法合理、有效。

配电网； 负荷； 多时段； 动态重构； 网损优化； 量子粒子群算法

PACS:03.65.-w

配电网重构的研究内容主要包含静态重构和动态重构两类，其中针对恒定负荷的静态重构[1-5]主要是对单个时间断面的配网负荷数据、约束条件进行简单优化组合，各时刻之间的优化方案缺乏联系，很难适应多个连续时间段负荷变化的运行领域，不能满足实际要求，因此缺乏一定的实用性。由于实际配电系统中的负荷是随时间动态变化的，为保证配电系统的安全可靠运行，需对配电网络结构进行动态调整，考虑多个连续时间区间内的配网负荷波动情况、开关操作次数变化的全局性优化重构。因此，配电网动态重构更具有实际意义。

针对负荷变化的配电网动态重构是一类复杂的时间优化组合问题，除满足恒定负荷下静态重构所需的各种约束条件外，还需对整个时间区间内的开关操作次数及重构次数做一定限制。文献[6]将开关操作次数作为限制条件，对每个时间断面利用混合粒子群算法分别进行求解，引入多代理协调优化方法来得到动态解；文献[7]利用功率矩法对重构时段进行动态划分进而控制最大重构次数；文献[8]对最优流计算方法进行改进，采用启发式规则来约束开关操作次数；文献[9]以整个时间区间内节约的有功电量最大化来选择开关开闭，通过修改物理寻优判据对开关操作次数进行约束。文献[6-9]都是按时间顺序对配电网进行动态重构，开关操作次数缺乏合理分配，无法保证在整个研究区间内动态重构结果的质量。文献[10]从提高电压稳定性的角度对所有时间断面进行物理寻优，缺少对开关次数限制的考虑；文献[11]只考虑网损最小的重构，结果导致开关操作次数过于频繁。

鉴于以上方法的不足，本文以配电网有功损耗最少和开关操作次数最少为综合优化目标对配电网进行动态重构研究，提出一种新型整数编码型量子粒子群优化算法对重构时段进行初步划分，并在初步优化的基础上进行二次优化，该方法不仅满足配电网开关操作次数约束也能有效减少重构次数。

1 网络重构模型及约束条件

1.1 目标函数

以配电网整个时间区间内的总有功损耗最少化和开关动作总次数最少化构建多目标优化模型。

总有功损耗最少化目标函数为

(1)

式中：T为负荷曲线划分后的时段数；N为配电系统的支路总数；Sn,j为支路n在第i时段的有功功率损耗；Pn,i、Qn,i和Un,i分别为支路n在第i时段系统流过其首端或者末端的有功、无功功率和电压；Δti为时段i的长度；rn为支路n的电阻。

开关操作次数最少化目标函数为

(2)

式中：M为可操作的开关总数；xk,j为开关k在时段i的状态，其值为0时表示开关打开，为1时表示开关闭合。

在构建配电网多目标动态重构模型中，由于二者的量纲不同，因此对总有功损耗和开关操作次数进行归一化处理，并采用线性加权方法将多目标优化转化为单目标优化，其综合优化目标函数为

(3)

式中：F(t)为t时刻的综合优化目标；λ1、λ2分别表示t时刻的有功损耗和开关操作次数的权重系数，且满足λ1+λ2=1；fploss(t)、fswitch(t)分别表示为t时刻系统的网损和开关操作次数；hploss、hswitch分别表示为配网重构时的初始网络损耗和实现配网重构时的初始开关操作次数。

1.2 约束条件

(1)潮流约束

(4)

式中：A为节点-支路关联矩阵；D为负荷需求矢量；P为馈线潮流矢量。

(2)支路容量约束

Sl≤Slmax。

(5)

式中：Sl为流过第l条支路的功率；Slmax为流过第l条支路所允许的最大功率。

(3)节点电压约束

Uimin≤Ui≤Uimax。

(6)

式中：Ui为节点i的实际电压；Uimax、Uimin分别为节点i允许通过电压的上限和下限。

(4)网络拓扑结构约束

早期已经有学者认识到精力限制会对SI的质量有影响，Kade和Cartellieri在中分析了听-译时间差(ear-voice span,EVS)，认为译者的表现与工作记忆(working memory)有关，而短期记忆的数量与长度就受到精力资源的制约

配电网一般为闭环设计，开环运行，在配电网重构过程中始终保持辐射状结构且不存在孤岛现象。

g∈G。

(7)

式中：G为既无环网又无孤岛的网络拓扑结构，即所允许的辐射状网络拓扑结构；g为重构后网络拓扑结构。

(5)开关动作次数约束

(8)

式中：T为负荷曲线划分后的时段数；M为可操作的开关总数；xk,i为开关k在时段i的状态；xmax为所有开关动作次数的上限值；xkmax为开关k的动作次数上限值。

2 基于量子粒子群算法的 动态重构模型求解

2.1 整数型环网编码方案

配电网动态重构属于大规模非线性优化组合过程，需要对多个时段的开关状态进行组合，编码方案比单个时段的静态重构更为复杂。粒子群算法[12]的离散编码主要有二进制编码和整数型编码两种。配电网动态重构中编码的位数和解码的复杂度对其寻优效率有重要影响。配电网中各开关的工作状态有断开、闭合两种运行方式。若采用二进制编码方式，0代表断开，1代表闭合，动态重构中划分的时段数为T，可动作的开关数为M，则二进制编码位数为MT位。虽然这种编码方式运算简便，原理清晰，但是没有考虑配电网结构的自身优点，必然会引起变量维数的增大、搜索空间的激增，在动态重构过程中产生大量的不可行解，降低寻优效率。为了降低变量维数，本文采用整数型环网编码方案进行求解。

为满足配电网受网络辐射状拓扑结构的约束，网络中开关的运行方式不是任意组合的。闭合一个联络开关，将形成一个独立环路，必须在此环路中断开一个开关，且同一条支路上的开关不能重复断开，因此配网中所有开关的开闭组合即构成了动态重构方案。

以图1所示IEEE33节点配电系统为例，说明动态重构中的整数型环网编码方案。网络中共有5个联络开关，闭合后形成5个独立环路，独立环路数表示粒子的维数。图中虚线表示联络开关，实线表示分段开关。由支路7-6-5-4-3-2-20-19-18-33所确定的闭合回路为1号环网，对闭合回路内的支路编码为：1-2-3-4-5-6-7-8-9-10，编码的最后一位数为联络开关所在的支路。配电网运行时对于不在任何环网中的开关必须闭合，所以在动态重构中不需要对其进行编码。同理，IEEE33节点配电系统其他环路的整数型环网编码如表1所示。

图1 IEEE33节点配电系统

Fig.1IEEE33node distribution system

表1IEEE33节点系统整数型环网编码

Tab.1IEEE33node ring network coding system

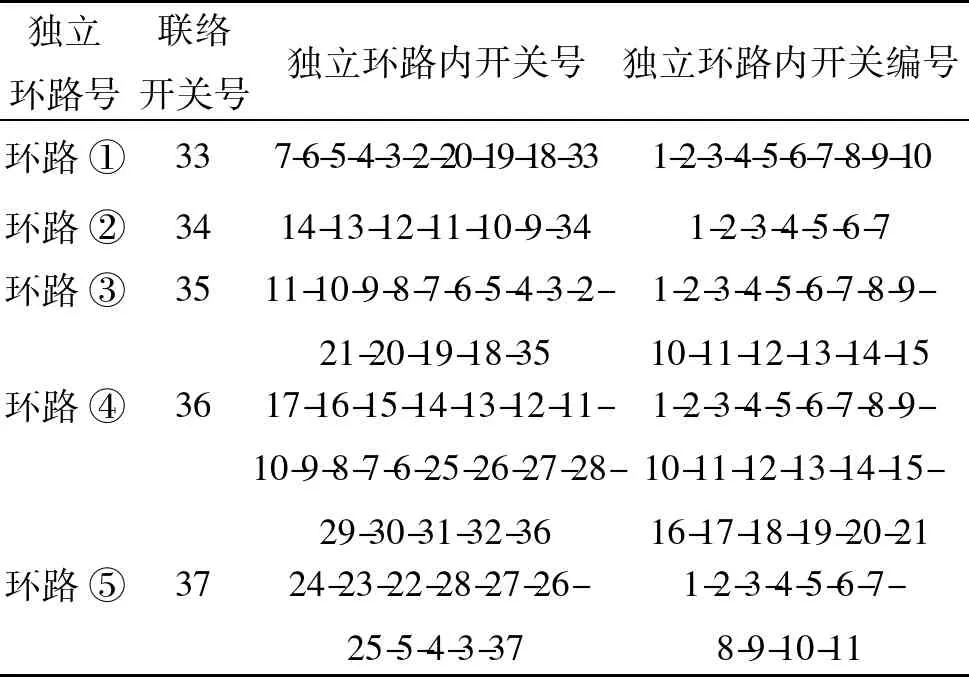
独立环路号联络开关号独立环路内开关号独立环路内开关编号环路①337-6-5-4-3-2-20-19-18-331-2-3-4-5-6-7-8-9-10环路②3414-13-12-11-10-9-341-2-3-4-5-6-7环路③3511-10-9-8-7-6-5-4-3-2-21-20-19-18-351-2-3-4-5-6-7-8-9-10-11-12-13-14-15环路④3617-16-15-14-13-12-11-10-9-8-7-6-25-26-27-28-29-30-31-32-361-2-3-4-5-6-7-8-9-10-11-12-13-14-15-16-17-18-19-20-21环路⑤3724-23-22-28-27-26-25-5-4-3-371-2-3-4-5-6-7-8-9-10-11

2.2 新型整数编码量子粒子群算法

传统的量子粒子群算法主要是用于解决连续的数值问题，各更新公式在计算处理时得到的数值均为实数，量子粒子群在迭代过程中产生的数值也均为连续的数。所以本文采用整数型环网编码方案，得到新型整数编码的量子粒子群算法(integer coded quantum particle swarm optimization, ICQPSO)。ICQPSO的粒子位置迭代方程和粒子进化方程如下

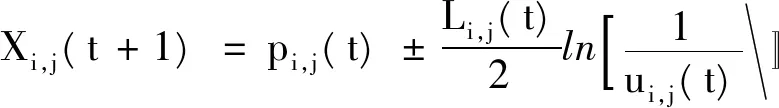
(9)

Li,j(t)=2α·|Cj(t)-Xi,j(t)|，

(10)

pi,j(t)=φj(t)·Pi,j(t)+φj(t)·Gj(t)，

(11)

(12)

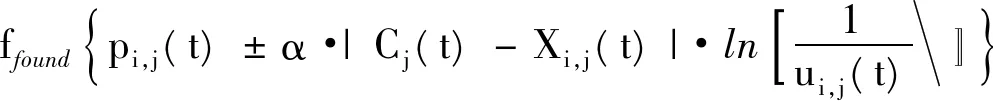
(13)

式中：pi,j(t)为粒子i的一个随机点位置坐标；Li,j(t)为δ势阱的特征长度，是进化方程中最重要的参量；ui,j(t)为区间(0,1)上均匀分布的随机数，即ui,j(t)～U(0,1);Cj(t)为所有粒子个体平均最好位置；Xi,j(t)为粒子i第t次迭代的位置；φj(t)为区间(0,1)上均匀分布的随机数，即φj(t)～U(0,1);Pi,j(t)为粒子i的个体最好位置坐标；Gj(t)为群体的全局最好位置；M为种群中的粒子数；N为粒子的维数；ffound函数表示将连续生成的实数转化为正整数解。α为收缩-扩张系数，定义为

(14)

式中：α值随着迭代的增加，线性地从α1递减到α0。一般取α1=1，α0=0.5，α0是控制参数的初始值，α1是控制参数的终止值，Gmax是总的迭代次数，G是当前的迭代次数。

在可行域内选择一个初始点，利用随机数的概率特性，产生若干个随机方向，并从中找出一个能使目标函数值下降最快的随机方向作为可行搜索方向。从初始点出发，由迭代方程计算出粒子的最新位置，并对每个更新后的粒子进行可行解判断，若解可行，则根据优化函数计算并更新粒子的个体最好位置和群体的全局最好位置；若不可行，则将该粒子的初始局部最优位置设为一个较大的正数，直到在可行域中求出一个最优解。

粒子的每一维表示每个环中应断开的开关，环内的开关数不同，则每一维的上下限也不同，因而需要设定粒子每一维的初始上下限。

Ua=(Ua1,Ua2,…UaN)，

(15)

La=(La1,La2,…LaN)。

(16)

式中：Ua为粒子每一维的初始化上限矩阵；La为粒子每一维的初始化下限矩阵；UaN为粒子i的第N维初始化上限；LaN为粒子i的第N维初始化下限。

2.3 开关环路矩阵与节点分层策略的 不可行解判定

33节点系统存在5个基本回路，当联络开关全部闭合时，必须在每一个回路中断开一个支路开关，并且这些独立回路又包含许多公共开关，因此在动态重构中将产生大量的不可行解。为保证网络动态重构后，配电网的拓扑结构依然满足闭环设计，开环运行，即没有孤岛和环网存在。现采用开关环路矩阵与节点分层策略对不可行解进行判定。判定方法如下，建立开关-环路关联矩阵L，即

式中：矩阵的行和列分别表示IEEE33节点配电系统所形成的5个回路和粒子的每一维所断开的开关编号；矩阵中的0和1分别表示开关在此回路和开关不在此回路。例如，S12=1表示所断开的开关存在于第2维的1号回路中。

当矩阵L为对角矩阵时，表示所断开的开关不是回路的公共开关，此时得到的解为可行解；当矩阵L不为对角矩阵时，表示所断开的开关存在于公共回路中，是回路的公共开关，则需判断是否出现环网，若不出现环网，则是可行解，否则，是不可行解。当矩阵L存在相同的两行，则表示同一开关被断开两次或者此开关为两个回路的公共开关被断开了两次，此时将会出现环网，形成不可行解。

当矩阵L不存在相同的行，出现复杂公共开关断开的情况，对于判定不可行解，开关环路矩阵已不再适用，需用节点分层策略判定是否为可行解。判定方法如下：

对配电网络中的节点进行分层，形成节点分层矩阵Y和其对应的上层节点矩阵Z。在该网络中除了首节点，都含有上层节点。因此，若上层节点矩阵Z中除了第一列元素为0外，其他列元素不为0，则得到的方案为可行解；否则为不可行解，即为出现环网或孤岛现象。

3 配电网多时段动态重构求解方法

本文分两步对时段划分进行优化，即时段的初步优化和时段的二次优化。

(1)时段的初步优化

在配电网多时段的初步优化中，利用等时间间隔划分方式将整个时间区间划分为多个时段，每个时段内的总负荷和节点负荷不变。以1h为时间间隔，将一天划分为24个时间段。具体流程如下。

步骤1：输入配电网原始数据，包括配网各负荷方式下的各节点负荷、各支路参数及初始结构等。

步骤2：采用等时间间隔的划分方式，并在划分后的时段内，计算网络在初始结构下的有功网损。

步骤3：利用量子粒子群算法在每个段落内进行一次静态重构，得到该段落的最优结构以及在该结构下的功率损耗。

步骤4：在上一步的基础上，若相邻时间段的开关动作方案相同，则把运行方式相同的相邻时段进行合并，并重新计算合并后时段的初始网损和重构后网损，更新现有时段。

(2)时段的二次优化

根据(1)中时段的初步划分结果，定义网络功率消耗指标，即

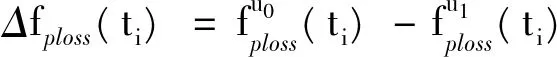
(17)

该功率消耗指标反映了网络的某个时段内运行在初始结构下的网损与重构后最优结构下网损之间的偏移程度。maxΔfploss(ti)为Δfploss(ti)(i=1,2,…,N)中的最大值，定义

Δfploss(ti)*=[Δfploss(ti)/maxΔfploss(ti)]×100%。

(18)

由Δfploss(ti)*构成功率消耗指标序列

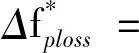
(19)

从而计算出功率消耗指标的极差为

RΔfploss=max(Δfploss(ti)*)-min(Δfploss(ti)*)。

(20)

功率消耗指标的标准差为

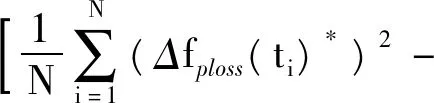
(21)

根据时段的初步划分方案，计算各划分时段的功率消耗指标，并设定功率消耗指标的最大极差和最大标准差，从而开始时段的二次优化。从初步划分后的第一个时段开始，逐次叠加时段，当功率消耗指标的极差和标准差波动较大时，则停止时段叠加，即认为一个时段划分结束，开始下一新时段，进行一次新的重构。

具体步骤如下。

步骤1：设定max RΔfploss和max SΔfploss初值以及最大允许重构次数，并计算每个时段内的功率消耗指标Δfploss(ti)。

步骤2：将第1个时段并入重构区间Ⅰ。

步骤3：将第2个时段并入重构区间Ⅰ，计算重构区间Ⅰ中时段1和时段2功率消耗指标的极差和标准差，若超过设定的max RΔfploss和max SΔfploss，则将时段2放入重构区间Ⅱ；否则将时段2并入重构区间Ⅰ。

步骤4：若时段2并入重构区间Ⅰ，则将时段3并入重构区间Ⅰ，重复步骤3；若时段2并入重构区间Ⅱ，则将时段3并入重构区间Ⅱ，计算重构区间Ⅱ中所有时段的功率消耗指标的极差和标准差，若超过设定的max RΔfploss和max SΔfploss，则将时段3放入重构区间Ⅲ。

步骤5：依次类推，直到所有时段全部划分完毕。

为了能够更好地降低重构次数和开关操作次数约束等限制条件，本文采用了逐次迭代法，调整max RΔfploss和max SΔfploss取得最优方案。具体调整方式为：先设定max RΔfploss和max SΔfploss的初值，根据时段划分后的结果，将得到的时段数TS与最大重构次数GN比较，若时段数不等于最大重构次数，则对max RΔfploss和max SΔfploss的值进行调整，直至得到的时段数等于最大重构次数。令第i次迭代的最大极差为max RΔfploss(i)，最大标准差为max SΔfploss(i)，则第i+1次迭代的最大极差、最大标准差分别为

(22)

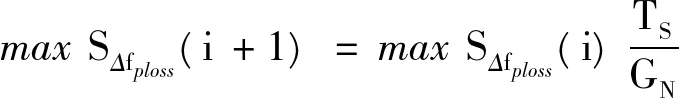
(23)

4 配电网动态重构主要步骤

应用上节所述时段优化求解方法，基于负荷变化的配电网多时段动态重构步骤为

(1)读入配电网系统的初始信息，包括各节点、支路和各时间段负荷参数。

(2)根据网络初始结构和各时刻系统负荷,将一天24h划分为若干重构时段。

(3)进行时段初步划分。即不考虑开关动作次数约束，对各个时段进行静态重构，将具有相同重构方式的相邻时段进行合并，得到开关动作方案。

(4)在初步划分的基础上，把所得到的开关动作方案作为搜索空间，并考虑最大重构次数、单个开关和总开关操作次数约束，进行时段的二次优化。

(5)输出动态重构的开关组合。

本文的配电网动态重构流程如图2所示。

图2 动态重构原理流程

Fig.2Flow chart of dynamic reconfiguration

5 算例分析

采用上述方法对图1所示IEEE33节点系统进行算例分析，以整个时间区间内总有功损耗和开关操作次数最少为多目标的配电网动态重构。此配电网络共包含33个节点，37条支路，其中有32条分段开关支路，5条联络开关支路(图中虚线所示)，基准电压为12.66kV，基准容量为100MVA，总负荷为3715kW+j2300kvar。以文献[13]中的负荷数据作为初始时段各节点的负荷值，研究时间为1d，时段可分为24个，每个时段1h，第1个时段为0：00—1：00，其他时段依次类推，并假设在任意自然时段(1h)内负荷保持恒定。负荷类型一般可分为工业、商业、居民负荷三种[14-15]，各节点中的负荷类型所占比例不同，同种负荷类型有相同的变化曲线。各类型负荷的时间分布如图3所示，各节点负荷组成比例如图4所示。

基于本文算法对上述配电系统进行动态重构，设种群规模为50，最大迭代次数为200，惯性权重因子w=1，学习因子c1=c2=2。经初步优化后，整个时段划分为7段，各自然时段重构初步划分结果如表2所示，重构前后系统各时刻网损变化情况如图5所示。

图3 三种负荷的时间分布

Fig.3Load distribution in times of three types load

图4 各节点负荷组成比例

Fig.4Load proportions for different nodes

表2 时段初步划分结果

Tab.2Preliminary results of the period divided

时段数重构结果网损/kW操作次数7重构时段断开开关重构前重构后1—67，14，9，32，287—87，14，9，32，379—127，14，9，32，2813—147，14，9，32，3715—177，14，9，32，2818—217，14，9，32，3722—247，14，9，32，282211．151524．5722

图5 重构前后各时刻有功损耗

Fig.5Reconfiguration power loss before and after each time

通过表2可以看出，重构次数和开关操作次数都大大增加，所以在时段初步优化的基础上，用量子粒子群算法对其最大重构次数及开关操作次数进行时段的二次优化。通过图5可以看出，重构后各时段的有功损耗明显低于重构前的有功损耗。图6为其中第12时段的收敛曲线，通过上图可以看出，该算法有较快的收敛速度，经过多次迭代后能够搜索到最优解，由此可见，该算法在优化该类问题时的有效性。当设定最大重构次数为4次时，得出各时段二次重构的最优时刻和结构偏移度序列如图7所示。时段划分后重构区间I为1—8段，重构区间II为9—15段，重构区间Ⅲ为16—21段，重构区间Ⅳ为22—24段。

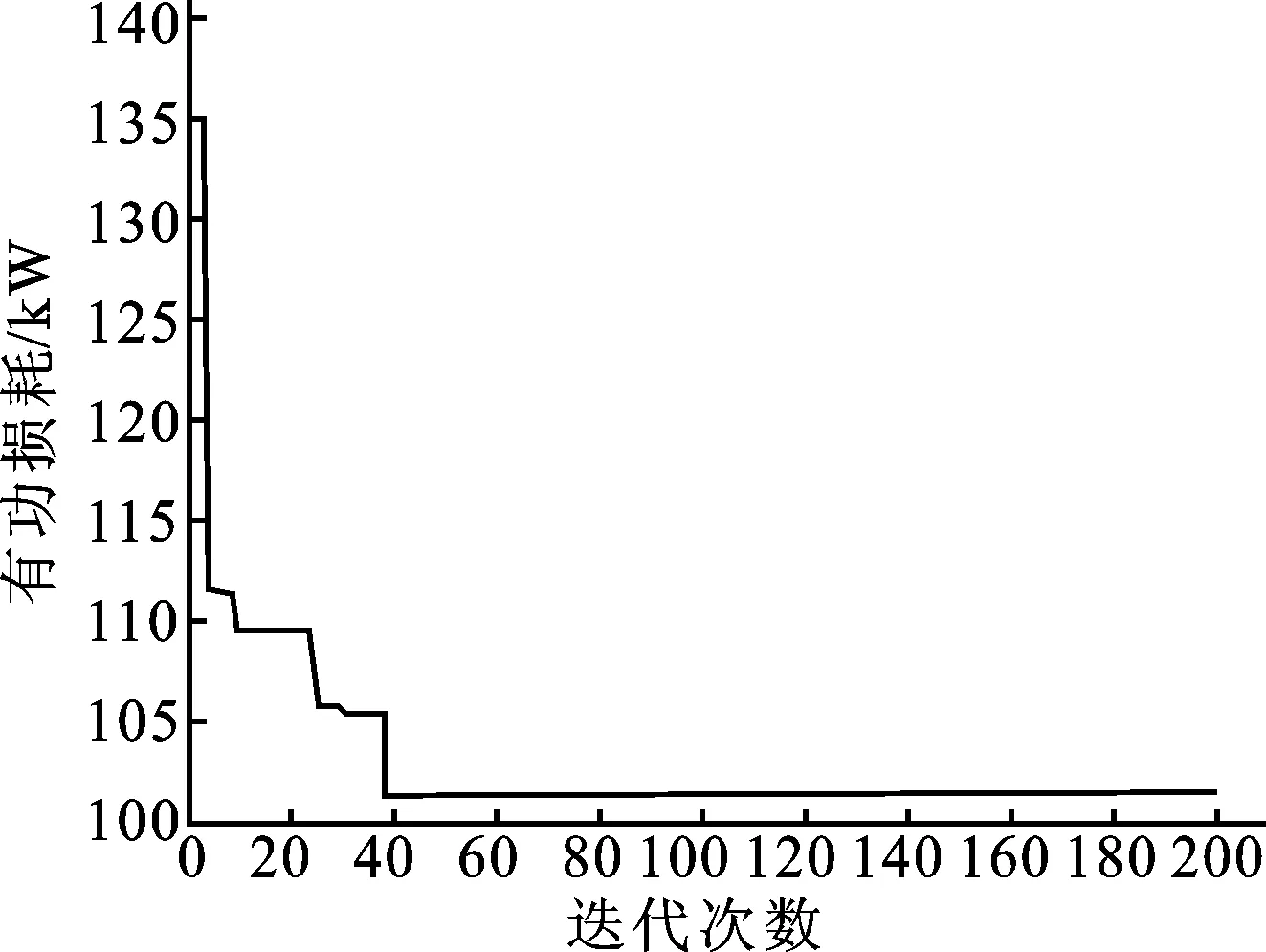
图6 ICQPSO的收敛特性曲线

Fig.6Convergence property curves of the ICQPSO

图7 重构区间划分

Fig.7Reconstruction interval divide

通过表3可以看出重构时间在0:00、8:00、15:00、21:00的开关动作方案相同，所以本文最优的动态重构方案如表4所示。

表3 二次优化结果

Tab.3 Results of Secondary optimization

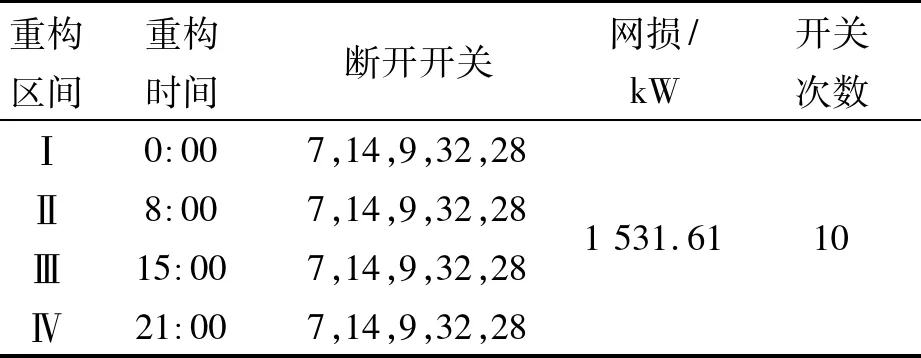
重构区间重构时间断开开关网损/kW开关次数Ⅰ0:007，14，9，32，28Ⅱ8:007，14，9，32，28Ⅲ15:007，14，9，32，28Ⅳ21:007，14，9，32，281531．6110

表4 动态重构方案

Tab.4 Dynamic reconfiguration scheme

重构次数重构时间断开开关网损/kW开关次数0———33，34，35，36，372211．1510:007，14，9，32，281531．6110

6 结论

由于实际配电网中的负荷随时间不断变化，本文提出了一种基于量子粒子群算法的配电网多时段动态重构新方法，该方法以配网有功损耗和开关操作次数最少为多目标函数，实际操作性强，且针对配网负荷的不断变化，能够更好地适应网络结构动态调整，反映配网中各时段的网损变化及开关操作情况。对配电系统的仿真验证了本文所提基于量子粒子群优化算法的配电网多时段动态重构方法的有效性，主要内容与结论如下：

(1)提出了开关环路矩阵与节点分层判别方法，提高了全局寻优能力。

(2)提出了基于独立环路的整数型环网编码策略，降低了动态优化的计算量。整数编码型量子粒子群优化算法具有良好的全局搜索能力，并能以较快的速度收敛到全局最优解。

(3)提出了针对负荷变化的配电网多时段动态重构方法，更能满足配网实际运行情况。

(4)提出了基于时间区间的初步优化，并在初步优化的基础上进行了二次优化，该方法不仅能够有效降低网损，满足开关约束等限制条件，同时也大幅度降低了重构次数，使重构方案更加合理可靠。

[1] CARRENO E M，ROMERO R， PADILHA-FELTRIN A．An efficient codification to solve distribution network reconfiguration for loss reduction problem[J]．IEEE Transactions on Power Systems，2008，23(4)：1542-1551．

[2] 黄红程，顾洁，方陈．基于无向生成树的并行遗传算法在配电网重构中的应用[J]．电力系统自动化，2015，39(14)：89-96．

[3] 黄伟，纪双全．基于馈线偶的配电网快速减小网损重构方法[J]．电力系统自动化，2015，39(5)：75-80．

[4] 陈春,汪沨,刘蓓,等．基于基本环矩阵与改进和声搜索算法的配电网重构[J]．电力系统自动化，2014，38(6)：55-60．

[5] 黄弦超，杨雨．基于电流分点编码的遗传算法在配电网重构中的应用[J]．电力系统自动化，2013，37(19)：74-79．

[6] 李振坤，陈星莺，赵波，等．配电网动态重构的多代理协调优化方法[J]．中国电机工程学报，2008，28(34)：72-79．

[7] 江东林，刘天琪，李樊．采用时段动态划分和分层优化策略的配电网重构[J]．电网技术，2012，36(2)：153-157．

[8] 刘蔚，韩祯祥．基于时间区间的配电网重构[J]．电力系统自动化，2006，30(10)：33-38．

[9] 尹丽燕，于继来．多时间段落的配电网络动态重构 [J]．中国电机工程学报，2002，22(7)：44-48，80．

[10] MISTRY K，ROY R．Enhancement of voltage stability index of distribution system by network reconfiguration including static load model and daily load curve[C]//Innovative Smart Grid Technologies．Kollam，India：IEEE Power Electronics Society，2011：17-22．

[11] ZIDAN A，EL-SAADANY E F．Multi-objective network reconfiguration in balanced distribution systems with variable demand[C]//2nd International Conference on Electric Power and Energy Conversion Systems．Sharjah，United Arab Emirates：IEEE，2011：1-6．

[12] 许立雄，吕林，刘俊勇．基于改进粒子群优化算法的配电网络重构[J]．电力系统自动化，2006，30(7)：27-30．

[13] BARAN M E, WU F F．Network reconfiguration in distribution systems for loss reduction and load balancing[J]．IEEE Transactions on Power Delivery，1989，4(2)：1401-1407．

[14] YIN S A，LU C N．Distribution feeder scheduling considering variable load profile and outage costs[J]．IEEE Transactions on Power Systems，2009，24(2):652-660．

[15] 杨胡萍，彭云焰，熊宁． 配网动态重构的静态解法[J]．电力系统保护与控制，2009，37(8)：53-57．

〔责任编辑 李 博〕

The application of quantum particle swarm optimization algorithm in multi-period dynamic reconfiguration of distribution network

WANG Wei， TAN Yanghong*

(College of Electrical and Information Engineering, Hunan University,Changsha 410082, Hunan, China)

In order to enhance the validity of the reconfiguration of the distribution network connected with time-varying loads, an original dynamic reconfiguration method of the distribution network at multi-period is proposed. To minimize the power losses and switching times, the dynamic reconfiguration model with multi-objective is built. Invalid solutions are quickly eliminated by using switch loop matrix and node-layering discriminative method. Further more, the dimensions of variables are diminished greatly with the help of integer loop code strategy. To solve this complicated model, an integer coded quantum particle swarm optimization algorithm is proposed to better deal with the dynamic reconfiguration of the distribution network. First, aiming at minimizing the power losses, the model is divided into different time periods; then based on the first division, the model is further divided in order to minimize the switching times.Thus, the optimal reconfiguration scheme is determined.The proposed method proves to be valid and reasonable supported by the results from the dynamic reconfiguration of the IEEE33node system.

distribution network；load；multiple time periods；dynamic reconfiguration；net loss optimization； quantum particle swarm optimization

1672-4291(2016)06-0031-08

10.15983/j.cnki.jsnu.2016.06.262

2016-04-29

国家自然科学基金(61102039，51577046)； 国家重点基础研究发展计划(973计划)(2012CB215106)；湖南省自然科学基金(14JJ7029)

TM715

A

*通信作者:谭阳红，女，教授，博士生导师。E-mail:309446238@qq.com