量子测量逻辑与推理理论

林运国， 李永明

(1福建农林大学 计算机与信息学院， 福建 福州 350002；2陕西师范大学 计算机科学学院， 陕西 西安 710119)



量子测量逻辑与推理理论

林运国1， 李永明2*

(1福建农林大学 计算机与信息学院， 福建 福州 350002；2陕西师范大学 计算机科学学院， 陕西 西安 710119)

已有的量子逻辑存在只适合于刻画封闭量子系统以及无法形式化量子测量算子等问题。为了描述开放量子系统，本文基于量子测量给出一种逻辑语言。首先，将经典命题公式作为逻辑语言的局部公式，以量子测量算子作为项公式；然后，将项公式的比较式和封闭量子子系统作为逻辑语言的原子命题，并定义一组量子联结词；最后，按结构归纳方式给出逻辑语言的全局公式。通过比较、分析已有的逻辑语言，说明量子测量逻辑的表达能力。作为公理化系统，给出量子测量逻辑的推理规则、元定理等相关理论。

量子逻辑； 量子测量； 元定理； 推理规则

量子逻辑是一种数学结构，是研究量子力学的逻辑基础。它不仅是关于量子力学的哲学、逻辑学的一个重要研究课题，而且还是物理学、数学(代数)的研究热点之一[1]。由于量子力学存在大量反直觉概念和理论，要想正确运用量子力学研究量子计算、量子信息，这就需要严格的数学证明或者严谨的逻辑推理。同时，要对量子系统进行逻辑推理，借助逻辑语言对系统属性或规范进行描述是必要的。因而，研究量子系统的逻辑语言成了研究量子计算必不可少的一个理论。

量子逻辑最早由毕克霍夫和冯诺伊曼[2]在1936年提出，企图诠释经典命题逻辑与关于量子力学隐变量测量事实之间的不一致性，说明描述量子力学的逻辑与经典逻辑存在着差异性。对于量子逻辑的研究，目前得到较为丰富的成果[3-10]。以毕克霍夫和冯诺伊曼的正交模格为基础扩展出来的量子逻辑, 仍然是量子计算研究领域中一个热点[3-4]。同时也存在其他不同类型的量子逻辑。比如，有些量子逻辑是将经典命题逻辑在量子环境下进行推广[5-6]；有些量子逻辑则用不满足交换律和结合律的MV代数来刻画[7,10]。

对于一个量子逻辑来说，其形式系统与现实原型之间应当具有相符性。具体来说，量子逻辑的联结词、基本算符、命题及其关系运算应当以量子力学实体和相关经验证据为理论背景。由此，近年来学者们开始从量子计算与量子信息角度研究量子逻辑，并且得到较好的研究成果和应用[11-12]。

作为经典命题逻辑在量子情形下的推广，Exogenous量子命题逻辑是目前较为成熟的一类量子命题逻辑[13]。Chadha等人利用Exogenous方法在经典命题逻辑基础上，增加项语言，用每个项公式表示某个测量结果发生的概率(振幅)，同时以两个项公式的比较式作为量子原子命题，并且给出量子联结词，施以结构归纳定义量子命题公式，从而构造出量子命题逻辑，还证明该逻辑具有可靠性和完备性。理论表明Exogenous量子命题逻辑作为经典命题逻辑在量子意义下的扩展，具有一定的表达能力，能够很好刻画BB84等量子通信协议。然而， Exogenous量子命题逻辑项公式的物理含义尚未解释。同时，该逻辑描述的是纯态，只能刻画封闭量子系统而不是开放量子系统。由于实际物理环境的干扰，量子系统往往具有开放性，因而如何逻辑刻画开放量子系统是值得研究的。另外，开放量子系统的量子态、系统演化和量子测量都是用算子表示的，如何从逻辑角度刻画算子和算子运算也是一个未解决的问题。为此，本文提出一种基于量子测量的逻辑语言，同时给出该逻辑的公理、推理规则、元定理等相关推理理论。

1 基本概念与符号规定

设H是一个由有穷量子比特所构成的有限维Hilbert空间。qB={qb1,qb2,…,qbn}是n个量子比特作为命题变元的一个集合，2qB是它的幂集。∀A∈2qB，如果qb∈A则qb赋值为真，编码为1；否则赋值为假，编码为0。此时称A为qB上一个赋值。2qB的每一个元素都对应qB上一个赋值，每一个赋值都可以用一个n位二进制进行编码，全体n位二进制编码构成qB上的全体赋值集。HqB是由2qB的全体元素作为一组标准正交基所张成的一个Hilbert空间，即HqB=span{|v〉|v∈2qB}。D(HqB)表示Hilbert空间HqB上所有正定且迹为1的算子的集合，即∀ρ∈D(HqB)，有ρ≥0且tr(ρ)=1。D(HqB)的元素称为密度算子，表示为量子系统的量子态。D-(HqB)表示Hilbert空间HqB上所有正定且迹小于等于1的算子的集合，即∀ρ∈D-(HqB)，有ρ≥0且tr(ρ)≤1。D-(HqB)的元素称为部分密度算子。L(HqB)是HqB上的有界线性算子空间；定义在L(HqB)上的线性算子，称为HqB上的超算子。HqB上的所有超算子的集合记为S(HqB)。令P(HqB)表示HqB上的投影测量算子集，即P(HqB)={P∈S(HqB)|P=P†=P2}。设v∈2qB，Pv表示测量结果为v的投影测量算子。

2 量子测量逻辑的构造

本节将基于Exogenous逻辑构造方法建立描述开放量子系统并且从形式化角度刻画和推理量子测量算子的逻辑语言，称为量子测量逻辑。该方法最早用于构造概率系统的逻辑语言[14]，包括三个层次：第一，把经典命题逻辑当作初始逻辑系统，经典命题公式称为局部公式；第二，基于经典命题逻辑系统，构造一套项语言，对系统属性进行定量描述；第三，将项公式的比较式作为原子命题，用以描述系统属性之间的关系，然后构造一套联结词并施以结构归纳定义逻辑语言的全局公式。

2.1 量子测量逻辑的语法

给定一个量子系统HqB，qB是系统对应的量子比特集。量子测量逻辑语法由三部分组成，见表1。

表1 量子测量逻辑的语法

Tab.1 Syntax of quantum measurement logic

组成部分公式构造经典命题公式a d⊥C|qb|α→Cα项公式t dO|I|x|∫α|t+t|tt|t⊗t量子测量公式γ dt≤t|[G]|⊥Q|γ→Qγ

经典命题公式是量子测量逻辑的局部公式,它是将n个量子比特{qb1,qb2,…,qbn}作为经典原子命题，通过使用联结词┐C、∨C、∧C、→C和↔C并施以结构归纳构造经典命题公式。其中┐C、∨C、∧C、→C和↔C分别表示否定、析取、合取、蕴涵和双蕴涵；⊥C表示经典永假式；下标C表示经典命题逻辑。所有经典命题公式之集记为ΓC(qB)。在量子测量逻辑中，每一个经典命题公式表示一个量子测量结果。

项公式表示量子测量算子，其论域为HqB上的投影测量算子集P(HqB)。其中O、I分别表示零算子、恒等算子；x表示自由变元；∫α表示投影测量算子，其测量结果使经典命题公式α为真命题；t+t、tt、t⊗t分别表示投影测量算子和、投影测量算子乘积、投影测量算子的张量积。所有项公式记为Term(qB)。每一个项公式表示为得到某一个测量结果所对应的量子测量算子。

量子测量公式是量子测量逻辑的全局公式。其中，t≤t和[G]是原子命题，分别表示两个项公式的比较式和封闭量子子系统；⊥Q表示量子永假式；γ→Qγ表示量子蕴涵公式，其中称→Q为量子蕴涵联结词；下标Q表示量子测量逻辑，区别于下标C。所有量子测量公式之集记为ΓQ(qB)。每一个量子测量公式表示测量结果之间的比较。

量子测量逻辑从量子测量角度出发，对测量结果的逻辑关系进行刻画，间接地描述开放量子系统的状态属性。记量子测量逻辑为EQML。

2.2 量子测量逻辑的语义

根据语法构造将EQML的语义解释分为3个部分：经典命题公式的赋值，它保持经典语义不变；项公式取为投影测量算子；量子测量公式的赋值。关于量子测量公式的赋值表述如下。

定义1[14]给定一个密度算子ρ，M(n,C)是一个复值线性算子集合，构造一个三元组〈HqB,M(n,C),Qρ〉使得∀A∈M(n,C)，有Qρ(A)=tr(Aρ)，则称该三元组为一个量子概率空间。

定义2给定一个量子概率空间〈HqB,M(n,C),Qρ〉,∀A1、A2∈M(n,C)，定义A1≤A2当且仅当对于给定的ρ∈D(HqB)，有tr(A1ρ)≤tr(A2ρ)。

给定一个密度算子ρ，对量子测量公式的语义定义如下。

(1)t1≤t2的真值解释为：t1≤t2为量子真命题当且仅当t1≤ρt2，否则称为量子假命题；

(2)[G]的真值解释为：[G]为量子真命题当且仅当ρ∈[G]，否则称为量子假命题；

(3)⊥Q为量子永假式；

(4)γ→Qγ的真值解释为：γ1→Qγ2为量子真命题当且仅且γ1为量子假命题或者γ2为量子真命题，否则称为量子假命题。

例如，设qB={qb1,qb2}，取α=qb1∧qb2和β=┐qb1∧┐qb2，则∫α和∫β分别表示投影测量算子P11=|1〉〈1|和P00=|0〉〈0|。给定一个密度算子ρ，∫β≤∫α为量子真命题当且仅当P00≤P11，该公式表示在量子状态ρ上的测量结果为11的概率大于等于测量结果为00的概率。比如，设ρ=0.2|00〉〈00|+0.8|11〉〈11|,则∫β≤∫α赋值为真；设ρ=0.6|00〉〈00|+0.4|11〉〈11|,则∫β≤∫α赋值为假。

2.3 几种常用的量子联结词

为了丰富量子测量公式，引入如下几种常用的量子联结词。

(t2≤t1);

γ2);

(γ2→Qγ1);

2.4 几种逻辑语言的对比分析

2.4.1 Exogenous概率命题逻辑和Exogenous量子命题逻辑 基于Exogenous逻辑构造方法最早由Baltazar[14]提出，用来构造概率命题逻辑，称为Exogenous概率命题逻辑，记为EPPL。其逻辑语法见表2。

表2 Exogenous概率命题逻辑的语法

Tab.2 Syntax of exogenous probability proposition logic

组成部分公式构造经典命题公式α d⊥C|p|α→Cα项公式t dr|∫α|t+t|tt，其中r∈R(实闭域)概率命题公式γ d[α]|t≤t|⊥P|γ→Pγ

该逻辑语法中，经典命题公式是局部公式，用来描述概率系统的定性属性，其中p是经典原子命题。项公式表示局部公式所描述概率系统的属性以及发生的概率，比如，∫α表示概率系统属性α出现的概率或者α为真命题的概率。概率命题公式是全局公式，其中以t≤t和[α]为原子命题。t≤t是两个项公式的一种定量比较，表示系统属性之间的大小关系，比如，∫α1≤∫α2表示使公式α1为真命题的概率小于等于使公式α2为真命题的概率。[α]表示使公式α为真命题的系统状态集。⊥P和→P是该逻辑的联结词，P表示概率系统。概率命题公式是通过原子命题t≤t和[α]并使用联结词⊥P和→P施以结构归纳形成得到的。

Chadha等人将Exogenous概率命题逻辑在量子意义下进行推广，称为Exogenous量子命题逻辑[13]，记为EQPL。其逻辑语法见表3。

表3 Exogenous量子命题逻辑的语法

Tab.3 Syntax of exogenous quantum proposition logic

组成部分公式构造经典命题公式a d⊥C|qb|α→Cα项公式t dx|0|1|t+t|tt|Re(u)|Im(u)‖u‖∫αu dz‖T〉GA|t+it|珔u|u+u|uu|α▷u;u量子命题公式γ dα|t≤t|[G]|⊥Q|γ→Qγ

Exogenous量子命题逻辑用来刻画封闭量子系统。在该逻辑语法中，经典命题公式、量子命题公式的含义与量子测量逻辑中的经典命题公式和量子测量公式是一致的。项公式是由2个部分递归构造而成，其论域是实闭域。项公式表示量子系统所处状态的概率或者概率振幅，比如，∫α表示经过量子测量之后量子系统属性α出现的概率或者说α为真的概率。|T〉GA表示投影测量的概率振幅，由于概率振幅可能是复数，所以引入虚根逻辑符号i、复数逻辑符号t+it、实部逻辑符号Re(u)和虚部逻辑符号Im(u)。Exogenous量子命题逻辑项公式的构造基本思想与Exogenous概率命题逻辑的项公式是一致的。

对比这3种逻辑EQML、EPPL和EQPL，EQPL和EQML都是在量子意义下对EPPL进行推广得到的。其中，EQPL用来刻画封闭量子系统；而EQML用来刻画开放量子系统。值得注意的是，EQPL和EQML最主要区别在于项公式的构造上。EQPL的项公式论域是实闭域，它表示概率或者概率振幅，适合于刻画封闭量子系统的状态(纯态)，但却无法刻画开放量子系统的状态(混合态)。由于开放量子系统的状态用密度算子来表示，同时用量子测量算子计算出系统所处的状态以及概率，因而需要涉及算子之间的运算。EQPL的项公式无法刻画量子算子及运算，而EQML的项公式用投影测量算子来表示。因而，EQML可以很好刻画量子测量运算。另外，EQPL的项公式物理含义仍然未得到解释；而EQML的项公式解释在投影测量算子集上，具有实际的物理意义。

2.4.2 经典命题逻辑 在量子测量逻辑的语法构造中，量子测量公式和经典命题公式在构造形式上是一致的，但在语义上有本质区别。下面通过剖析几个联结词的含义来区别这两种逻辑系统。

(1)→C与→Q

在经典命题逻辑中，考虑经典命题公式qb1→Cqb2，它表示如果测量结果是qb1则蕴含测量结果qb2的出现，那么称联结词→C为经典蕴含。在量子测量逻辑中，与该公式相对应的量子测量公式是◇qb1→Q◇qb2(不存在量子测量公式qb1→Qqb2)。该公式表示如果测量结果qb1可能出现那么蕴含测量结果qb2的可能出现，则称联结词→Q为量子蕴含。类似地，还有必然出现的量子蕴含：□qb1→Q□qb2。下面实例说明在经典态和混合态下这两种联结词存在差异性。

表4给出系统处于4种经典状态时，qb1→Cqb2与◇qb1→Q◇qb2的逻辑取值情况。由表4可知，qb1→Cqb2与◇qb1→Q◇qb2逻辑取值是一致的。这是因为对每一种状态，系统都只有一个测量结果，亦即00、01、10和11的其中一个。比如当ρ=|00〉〈00|时，由于测量结果为00，则qb1→Cqb2取真值；而对于◇qb1→Q◇qb2，由于取投影测量算子∫qb1=|1〉〈1|和∫qb2=|1〉〈1|，经过计算◇qb1和◇qb2各取假值，所以◇qb1→Q◇qb2取真值。表4中还给出概率蕴含公式◇qb1→P◇qb2和量子必然公式□qb1→Q□qb2，它们取值情况与前两种是一致的。

表4 经典状态下的→C与→Q的对比

Tab.4 Contrast of →Cand →Qunder classical states

ρqb1→Cqb2◇qb1→Q◇qb2◇qb1→P◇qb2□qb1→Q□qb2|00〉〈00|TTTT|01〉〈01|TTTT|10〉〈10|FFFF|11〉〈11|TTTT

注：“T”、“F”各表示命题取真值和命题取假值。

表5给出混合态下各种蕴含公式的取值情况。当ρ=p|00〉〈00|+(1-p)|01〉〈01|时，如果测量结果是00，则qb1→Cqb2为真命题；而对于◇qb1→Q◇qb2，由于取投影测量算子∫qb1=|1〉〈1|和∫qb2=|1〉〈1|，经计算◇qb1和◇qb2分别取假值和真值，所以◇qb1→Q◇qb2为真命题。当ρ=p|00〉〈00|+(1-p)|10〉〈10|时，由于测量结果可能是00也可能是10，所以qb1→Cqb2可能为真命题也可能为假命题；而对于◇qb1→Q◇qb2，◇qb1和◇qb2分别取真值和假值，则◇qb1→Q◇qb2为假命题，因而在混合态下经典蕴含和量子蕴含是不一样的。表5还给出量子必然蕴含公式和概率蕴含公式的真值，其中概率蕴含公式的真值本质上是一个概率分布。比如，当ρ=p|00〉〈00|+(1-p)|10〉〈10|时，◇qb1→P◇qb2为真命题的概率是p而为假命题的概率是1-p。

表5 混合态下的→C与→Q的对比

Tab.5 Contrast of →Cand →Qunder quantum mixed states

ρqb1→Cqb2◇qb1→Q◇qb2◇qb1→P◇qb2□qb1→Q□qb2p|00〉〈00|+(1-p)|01〉〈01|TTTTp|00〉〈00|+(1-p)|10〉〈10|T，FFT，FTp|00〉〈00|+(1-p)|11〉〈11|TTTTp|01〉〈01|+(1-p)|10〉〈10|T，FTT，FTp|01〉〈01|+(1-p)|11〉〈11|TTTTp|10〉〈10|+(1-p)|11〉〈11|T，FTT，FT

注：“T，F”表示可能为真值也可能为假值。

(2)∧C与∧Q

表6给出经典命题公式qb∧C┐Cqb与量子测量公式◇qb∧Q◇┐Cqb的对比。不管ρ=|0〉〈0|还是ρ=|1〉〈1|，经典命题公式qb∧C┐Cqb与量子测量公式◇qb∧Q◇┐Cqb都是永假式(经典或量子)。然而，当系统处于混合态时，两个公式的真值并不一定相同。比如，当ρ=p|0〉〈0|+(1-p)|1〉〈1|时，不管测量结果是0还是1，经典命题公式是经典永假式；而对于量子测量公式◇qb∧Q◇┐Cqb，由于∫qb=|1〉〈1|和∫┐Cqb=|0〉〈0|，◇qb和◇┐Cqb都取真，所以◇qb∧Q◇┐Cqb为真命题。这不是一个矛盾的事实，因为对于一个量子系统同时处于两种不同状态是可能的，即处于叠加态。

(3)⊥C与⊥Q

在经典命题逻辑中，经典永假式⊥C可定义为qb∧C┐Cqb；而在量子测量逻辑中，量子永假式⊥Q可定义为◇qb∧Q┐Q◇qb。不难计算出⊥C与⊥Q是逻辑等价的，见表6。这也说明了矛盾的事实不管在经典世界里还是在量子世界里都是错误的。

表6 ∧C与∧Q的对比

Tab.6 Contrast of ∧Cand ∧Q

ρqb∧C┐Cqb◇qb∧Q◇┐Cqb|0〉〈0|FF|1〉〈1|FFp|0〉〈0|+(1-p)|1〉〈1|FF

3 薛定谔猫的逻辑刻画

薛定谔猫是奥地利物理学家薛定谔提出的一个量子思想上的实验，主要阐述量子叠加态原理[15]。它假设：将一只猫关在一个带有少量镭和氰化物的封闭容器中，其中镭会以一定几率存在衰变。如果镭发生衰变，它会激发开关打碎装有氰化物的瓶子，从而毒死猫；否则，猫就安全活着。根据量子力学的基本理论，镭会处于衰变和没有衰变两种状态的叠加，所以猫也会处于活着和死了的叠加状态。这种既活又死的猫就是所谓的“薛定谔猫”。

考虑一只薛定谔猫，它有3种属性：猫在容器中qbbox；猫活着qbalive；猫是动的qbmoving。因而，该量子系统的量子比特命题符号集可以表示为qB={qbbox,qbalive,qbmoving}。

利用量子测量逻辑可以刻画薛定谔猫，表述如下：

(1)原子命题[{qbbox,qbalive,qbmoving}]表示由这3个量子比特的Hilbert空间是一个封闭量子系统；

(2)经典公式qbmoving→Cqbalive表示如果猫是动的，那么它是活着；

(3)原子命题┐Q[qbalive]或[qbalive,qbmoving]表示单量子比特qbalive的赋值集张成的Hilbert空间不是一个封闭量子系统，它一定与量子比特qbmoving纠缠在一起。因为如果对第一个量子比特qbalive进行测量，得到的测量结果是alive，那么对第二个量子比特的测量结果可能是moving；同样，如果对第二个量子比特qbmoving进行测量，得到的测量结果是moving，那么对第一个量子比特的测量结果一定是alive；

(4)量子测量公式(0<∫qbalive)∧Q(0<∫┐qbalive)表示猫是活着还是死的，这都是有可能的；

(5)量子测量公式

([{qbalive,qbmoving}])∧Q

(∫qbalive∧Cqbmoving=p1I)∧Q

(∫qbalive∧C┐qbmoving=p2I)∧Q

(∫┐qbalive∧C┐qbmoving=p3I),

其中p1+p2+p3=1，该公式进一步阐述量子比特qbalive与量子比特qbmoving间的关系，说明了猫存在性只有3种可能性：如果它活着，可能是动的也可能是不动的；如果它是死的，那么它一定是不动的。

4 公理、推理规则与元定理

作为公理化系统，本节提出量子测量逻辑的公理、推理规则和元定理，进而给出量子测量逻辑的推理理论。

4.1 公理

公理1: |-γ,γ为量子永真式；

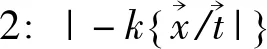
公理3: |-∫T=I(T为经典永真式)；

公理4:|-∫⊥C=O；

公理5:|-∫α1∧Cα2=O→Q∫α1∨Cα2=∫α1+∫α2；

公理6:|-∫α1→Cα2→Q∫α1≤∫α2;

公理7:|-[∅]；

公理8:|-[A]→Q([B]→Q[A∪B])；

公理9:|-[A]↔Q[B],其中A∪B=qB；

公理10:|-([A]∧Q[B])→Q(∫α1∧Cα2=

∫α1⊗∫α2),其中α1∈ΓC(A),α2∈ΓC(B)。

公理1表明量子永真式都是公理；公理2表明如果k是量子永真式，那么对项变元进行任何替代仍然是量子永真式；由于经典永真式出现的概率为1，所以公理3表明如果测量结果为经典永真式则其对应的投影测量算子应当取为恒等算子；同样，由于经典永假式出现的概率为0，所以公理4表明如果测量结果为经典永假式则其对应的投影测量算子应当取为零算子；公理5表明如果两个测量结果不会同时出现，那么两个测量结果至少有一个出现的概率应当等于两个测量结果对应概率的和，因而其对应的投影测量算子应当等于两个测量结果所对应的投影测量算子的和；公理6表明如果一个测量结果的出现必然导致另外一个测量结果的出现，那么前者发生的概率应当小于等于后者发生的概率，所以前者对应的投影测量算子小于等于后者对应的投影测量算子；公理7表明空的量子系统(量子比特集为空集)是封闭量子系统；公理8表明对于封闭量子系统[G1]，如果[G2]也是封闭量子系统，那么联合量子系统[G1∪G2]也是封闭的；公理9表明[G]是封闭量子系统当且仅当[qBG](qBG是G的补集)也是封闭量子系统；公理10表明两个独立量子子系统的联合测量结果发生概率等于两个各自测量结果发生概率的乘积，因而联合系统的投影测量算子应当取两个各自投影测量算子的张量积。

4.2 推理规则

对于量子测量公式集ΓQ(qB)(简写为Γ)，选择一个有限量子测量公式集作为公理集Λ，制定推理规则，由Γ∪Λ中的公式经过有限次使用推理规则得到的公式γ，那么称γ为Γ的定理，记为Γ|-γ。

选择假言三段论作为量子测量逻辑的推理规则，表述为从量子测量公式γ和γ→Qβ推出量子测量公式β，称为QMP，记为：γ,γ→Qβ|-β。

4.3 元定理

由量子测量公式、公理和推理规则以及Γ的定理，共同组成量子测量逻辑的公理化系统。关于该公理化系统所具有性质的定理，称为元定理。

定理1|-∫┐Cα>pI→Q┐Q(∫α>(1-p)I)。

证明根据公理3，∫T=I是一个量子永真式，作为它的特例∫┐Cα∨Cα=I也是一个量子永真式。再根据公理5，有∫┐Cα+∫α=I成立。设量子测量公式∫┐Cα>pI为真命题，其中0≤p≤1，则量子测量公式∫α≤(1-p)I也为真命题，因而推出┐Q(∫α>(1-p)I)为真命题。结论成立。

定理2设γ1、γ2、γ3是量子测量公式，则如果Γ|-γ1→Qγ2且Γ|-γ2→Qγ3,那么Γ|-γ1→Qγ3。

证明根据量子蕴涵联结词→Q的定义，可推出(γ1→Qγ2)→Q[(γ2→Qγ3)→Q(γ1→Qγ3)为一个量子永真式，记为η。如果Γ|-γ1→Qγ2，则推出Γ|-(γ1→Qγ2)∧η，利用QMP，逻辑推出Γ|-(γ2→Qγ3)→Q(γ1→Qγ3)。又因为Γ|-γ2→Qγ3，再利用QMP，逻辑推出Γ|-γ1→Qγ3。

定理3设Γ为量子测量公式集，γ1、γ2为任意两个量子测量公式，那么Γ∪{γ1}|-γ2当且仅当Γ|-γ1→Qγ2。

证明(1)若Γ∪{γ1}|-γ2，则有Γ|-γ1→Qγ2。

按公式结构归纳证明如下，分为两种情形：

(i)设γ2为量子永真式或是一个定理，即有Γ|-γ2。因为γ2→Q(γ1→Qγ2)为量子永真式，所以有Γ|-γ1→Qγ2。

(ii)设γ2是由γ和γ→Qγ2经QMP逻辑推理得到，且Γ∪{γ1}|-γ和Γ∪{γ1}|-γ→Qγ2。由归纳法证明可得Γ|-γ1→Qγ和Γ|-γ1→Q(γ→Qγ2)。因为[γ1→Q(γ→Qγ2)]→Q[(γ1→Qγ)→Q(γ1→Qγ2)]为一个量子永真式，所以有Γ|-(γ1→Qγ)→Q(γ1→Qγ2)，进一步有Γ|-γ1→Qγ2。因而结论成立。

(2)若Γ|-γ1→Qγ2,则有Γ∪{γ1}|-γ2。

因为Γ∪{γ1}|-γ1且Γ|-γ1→Qγ2，所以有Γ∪{γ1}|-γ1∧Q(γ1→Qγ2)，则有Γ∪{γ1}|-γ2成立。

作为定理3的推论，可得到定理4和定理5如下。

定理4如果Γ∪{γ}|-⊥Q,那么Γ|-┐Qγ。

定理5Γ,ψ|-┐Qφ当且仅当Γ,φ|-┐Qψ。

定理6给定量子测量公式γ1以及t1和t2为项公式，量子测量公式γ2是将γ1中凡是出现t1均用t2替代得到的，则|-(t1≡Qt2)→Q(γ1≡Qγ2)。

根据公理2可证得定理6。

定理7给定3个量子测量公式γ、γ1和γ2，设量子测量公式γ′是将γ中凡是出现γ1均用γ2替代得到的，则|-(γ1≡Qγ2)→Q(γ≡Qγ′)。

证明分为3种类型。

(1)设γ是一个量子永真式，则对γ进行任意替代得到的量子测量公式γ′均为量子永真式，所以|-(γ1≡Qγ2)→Q(γ≡Qγ′)成立。

(2)设γ是一个量子永假式⊥Q，类似于(1)证明可得结论成立。

(3)设γ=η1→Qη2是一个量子蕴含公式。设量子测量公式η1和η2中存在子公式γ1，将γ1替代为γ2，分别得到量子测量公式η1′和η2′，令γ′=η1′→Qη2′。若γ1≡Qγ2，则η1≡η1′和η2≡η2′。当η1→Qη2时，则有η1′→Qη2′。因而有(η1→Qη2)→Q(η1′→Qη2′)成立。同理有(η1′→Qη2′)→Q(η1→Qη2)成立，所以推出(η1′→Qη2′)≡Q(η1→Qη2),也就是γ≡Qγ′。

综合上述3种以情形有|-(γ1≡Qγ2)→Q(γ≡Qγ′)成立。

定理8如果Γ|-γ1,Γ|-γ2,…,Γ|-γ1且γ1,γ2,…,γn量子蕴含β，那么Γ|-β。

运用数学归纳法可证明定理8。

定义3给定一个量子测量公式集，如果某个量子测量公式β与┐Qβ都是它的定理，那么称它是不和谐的。

定理9若量子测量公式集Γ∪{φ}是不和谐的，则有Γ|-┐Qφ。

证明由于Γ∪{φ}是不和谐的，所以存在一个量子测量公式β使得Γ∪{φ}|-β和Γ∪{φ}-┐Qβ成立。根据定理3，有Γ|-φ→Qβ和Γ|-φ→Q┐Qβ成立，所以Γ|-┐Qφ。

4.4 纠缠态的推理判定

量子纠缠状态是指两个或多个量子系统之间的非定域的关联关系[15],它是实现信息高速的不可破译通信的理论基础。下面将利用量子测量逻辑以及推理理论给出两体态不可分离的逻辑判定。

根据公理10，则下列推断是成立的：

|-([A]∧Q[B])→Q(∫αAB=∫αA⊗∫αB),

其中αA、αB分别是ΓC(A)、ΓC(B)中一个极小项。

对于ΓC(A)、ΓC(B)所有极小项，有

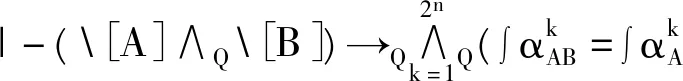
利用定理8有

根据公理9有[A]↔Q[B]或┐Q[A]↔Q┐Q[B]，进一步得到

5 结论

本文针对开放量子系统，从量子测量角度出发，进行量子测量算子以及运算的逻辑关系的研究。该逻辑系统具有一定的逻辑表达能力，能够很好刻画薛定谔猫。同时作为公理化系统，该逻辑系统具有一定的逻辑推理能力。作为进一步研究工作，我们将用该逻辑刻画实际开放量子系统，并且与已有的研究成果进行比较，并对该逻辑系统的表达能力进行全面研究。

[1] ENGESSER K, GABBAY D M, LEHMANN D. Handbook of quantum logic and quantum structures: quantum logic[M]. Netherlands: Elsevier,2009.

[2] BIRKHOFF G, NEUMANN J V. The logic of quantum mechanics[J]. Annals of Mathematics,1936, 37(4): 823-843.

[3] PYKACE J. B-vN quantum logic as -valued Lukasiewicz logic[M]//Quantum physics, fuzzy sets and logic. Berlin: Springer International Publishing,2015: 47-57.

[4] HARTONAS C. First-order frames for orthomodular quantum logic[J]. Journal of Applied Non-Classical Logics,2016,26(1): 69-80.

[5] PYKACZ J. Birkhoff-von neumann quantum logic[M]//Quantum physics, fuzzy sets and logic. Berlin: Springer International Publishing,2015:33-45.

[6] KRAMER S. Quantum logic as classical logic[EB/OL]. http://arxiv.org/abs /arxiv:1406.3526,2014.

[7] DUNN J M, MOSS L S, WANG Z H. The third life of quantum logic: quantum logic inspired by quantum computing[J]. Journal of Philosophical Logic,2013, 42(3): 443-459.

[8] VIGANO L, VOLPE M, ZORZI M. Quantum state transformations and branching distributed temporal logic[C]// KOHLENBACH U, BARCELP, QUEIROZ R D. Logic, language, information, and computation. Berlin: Springer International Publishing,2014:1-19.

[9] BERTINI R F, LEPORINI R. Logics from quantum computation with bounded additive operators[J]. International Journal of Quantum Information,2012,10(3):230-241.

[10] BLUTE R F, GUGLIELMI A, IVANOV I T, et al. A logical basis for quantum evolution and entanglement[C]//Categories and types in logic, language, and physics. Berlin: Springer International Publishing,2014: 90-107.

[11] GUDDER S. Quantum computational logic[J]. International Journal of Theoretical Physics,2003, 42(1): 39-47.

[12] CHIARA M L D, GIUNTINI R, SERGIOLI G, et al. Abstract quantum computing machines and quantum computational logics[J]. International Journal of Quantum Information,2016:1640019.

[13] MATEUS P, SERNADAS A. Weakly complete axiomatization of exogenous quantum propositional logic[J]. Information and Computation,2006,204(5): 771-794.

[14] BALTAZAR P. Probabilization of logics: completeness and decidability[J]. Logica Universalis,2013, 7(4): 403-440.

[15] NIELSEN M, CHUANG I L. Quantum computation and quantum information[M]. Cambridge: Cambridge University Press,2000.

〔责任编辑 宋轶文〕

Quantum measurement logic and its deduction theory

LIN Yunguo1, LI Yongming2*

(1College of Computer and Information Sciences, Fujian Agriculture and Forestry University, Fuzhou 350002, Fujian, China;2School of Computer Science, Shaanxi Normal University, Xi′an 710119, Shaanxi, China)

At present, several problems exist in quantum logics such as only being suitable for closed quantum systems and the inability to formalize quantum measurement operators. In order to model and reason about open quantum systems, a logical language is proposed based on quantum measurement. Firstly, classical propositional formulas are taken as initial and local formulas, and term formulas are interpreted as quantum measurement operators. Secondly, the comparative formulas between quantum measurement operators and closed quantum sub-systems are logically defined as atomic propositions. Meanwhile, a set of quantum connectives are introduced. Finally, global formulas of our logic are inductively built. By comparison and analysis about several logics, the expression power of our logic is illustrated. As an axiomatic system, the related deduction theories are studied such as the inference rule and meta-theorems.

quantum logic; quantum measurement; meta-theorem; inference rule

81P15

1672-4291(2016)06-0006-08

10.15983/j.cnki.jsnu.2016.06.162

2016-08-03

国家自然科学基金(11271237); 福建省自然科学基金(2016J01283); 福建省教育厅中青年教师教育科研项目(JA13115)

TP301.2

A

*通信作者：李永明,男,教授，博士生导师。E-mail:liyongm@snnu.edu.cn