利用圆心到直线的距离解题例说

◇ 湖北 陈克林



利用圆心到直线的距离解题例说

◇ 湖北 陈克林

直线与圆的位置关系问题的求解主要涉及2种方法:代数法和几何法．代数法通过将直线方程与圆的方程联立,代入消元后得关于x的一元二次方程,利用判别式及根与系数的关系寻找已知与未知的关联．几何法主要是利用圆心到直线的距离建立桥梁．本文主要从几何角度寻求问题的求解思路．

例1(2016年全国卷Ⅱ)圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=( ).

本题求解中直接利用点到直线的距离公式求出弦心距,结合已知距离建立含参数a的方程,解方程即可得出正确结果．下面对圆心到直线的距离在有关问题中的应用举例分析．

1 与面积有关的问题

例2过点(2,0)引直线l与圆x2+y2=2相交于A、B2点,O为坐标原点,当△AOB面积最大时,直线l的斜率为( ).

当直线l的斜率不存在时,l的方程为x=2,不符合题意．

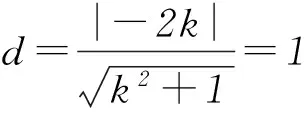
故正确选项为C.

变式设直线l:mx+ny-1=0 (m、n∈R*)与x、y轴相交于A、B2点,且l与圆x2+y2=19相交所得弦长为2,O为坐标原点,求△AOB面积的最小值．

解析由题设可知,直线l与2坐标轴的交点为A(0,1/n)、B(1/m,0)．

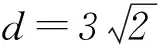
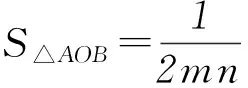
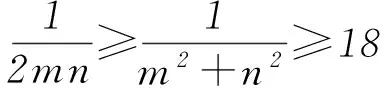
点评例2是求过定点的直线与圆相交所得的2个交点与圆心构成的三角形面积最值.变式中将过定点的条件改为直线与圆相交所得弦长为定值,利用平面几何性质构造出面积关系式,进而利用均值不等式求最值．

2 与相切有关的问题

例3(2015年江苏卷) 在平面直角坐标系xOy中,以点(1,0)为圆心且与直线mx-y-2m-1=0 (m∈R)相切的所有圆中,半径最大的圆的标准方程为________.

解析将方程mx-y-2m-1=0整理得y+1=m(x-2),即直线过定点D(2,-1).易知圆心C到直线mx-y-2m-1=0的距离小于等于|CD|,最大半径

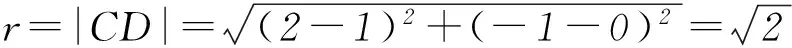
此时圆的标准方程为(x-1)2+y2=2.

变式在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心、1为半径的圆与圆C有公共点,则k的最大值是________.

解析圆C的方程可化为(x-4)2+y2=1,所以圆C的圆心为(4,0),半径为1．

由题意可知直线y=kx-2上至少存在一点A(x0,kx0-2),以该点为圆心、1为半径的圆与圆C有公共点，所以存在x0∈R,使得|AC|≤1+1成立,即|AC|min≤2．

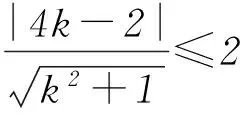
点评以上2例通过直线与圆相切、圆与圆相切,找到取得最值的位置,进而顺利求解．

3 与弦长有关的问题

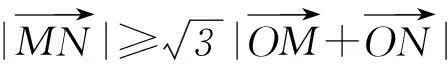
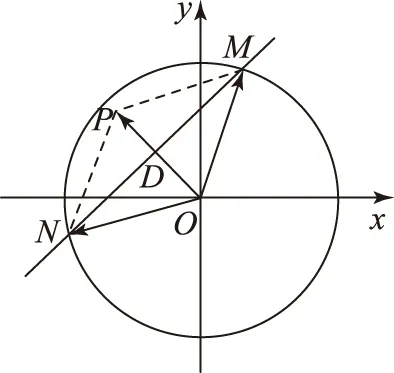
图1

C[-2,2];

解析如图1所示,由向量加法的平行四边形法则,知

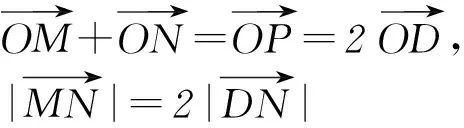
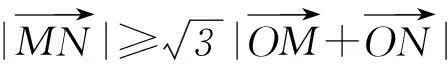
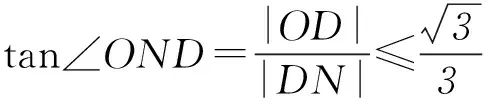
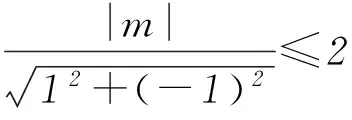
变式(2014年重庆卷) 已知直线ax+y-2=0与圆心为C的圆(x-1)2+(y-a)2=4相交于A、B2点,且△ABC为等边三角形,则实数a=________.

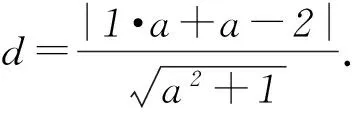
点评上述例4及变式均是通过将题目条件中所给几何关系等价转化为弦心距离问题,利用点到直线距离公式构造出不等式或方程来解决问题．

综上,可以看出圆心到直线的距离在上述问题的求解中起了重要的作用．深入挖掘题目的隐含条件,准确利用即可顺利解题．

湖北省咸宁市青龙山高中)