2016年高考数学四川卷理第20题的推广

◇ 江西 黄贤锋 北京 童嘉森(特级教师)



2016年高考数学四川卷理第20题的推广

◇ 江西 黄贤锋1北京 童嘉森2(特级教师)

(1) 求椭圆E的方程及点T的坐标.

(2) 设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的2点A、B,且与直线l交于点P.证明:存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.

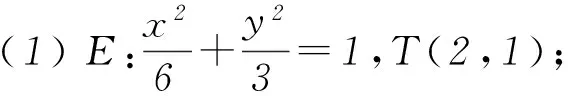
(2) 存在常数λ=4/5.

本题主要考查椭圆的标准方程及其几何性质,考查直线与椭圆的位置关系,以及利用“设而不求”的方法求相关线段的长;本题运用“几何问题代数化”的基本思想探究椭圆的切线和相关割线之间的内在联系,思辨性强.

回顾此题,笔者引发如下思考:常数λ与切点T究竟有怎样的内在联系?对于这样一对特殊的切线和割线,能否得出一般性的结论?该结论能否推广到双曲线和抛物线呢?

经过一番涂入思考,笔者得出了如下几个结论,希望能和大家共勉.

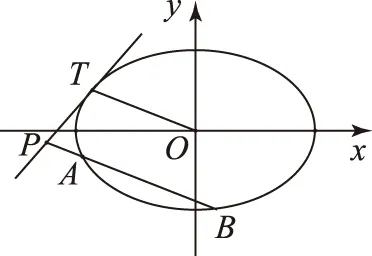
图1

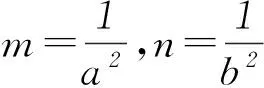
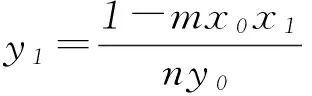
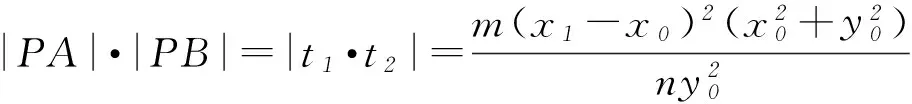
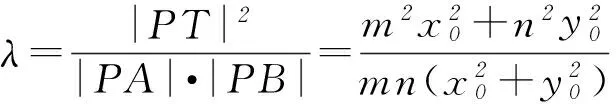
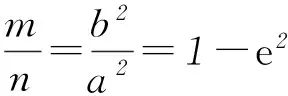
2) 当T为左、右顶点,即y0=0时,易得上述结论也成立.

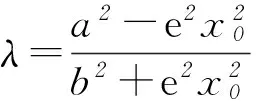
类比结论1,可得出双曲线中的类似结论.

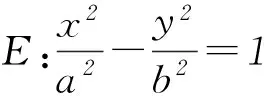
进一步得出抛物线中的类似结论.

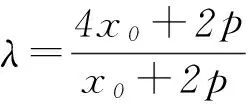
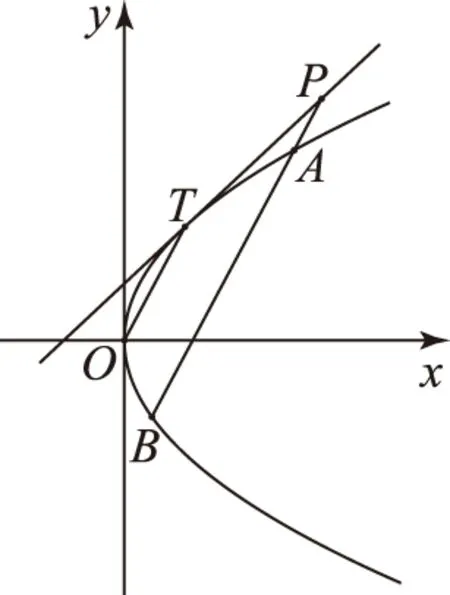
图2

证明如图2,设P(x1,y1),因为抛物线y2=2px的点T(x0,y0)处的切线l方程为y0y=p(x+x0),所以

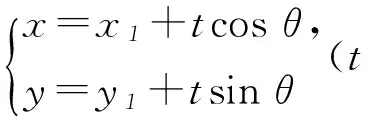
将l′的方程与抛物线方程联立代入,可得(y1+tsinθ)2=2p(x1+tcosθ),整理得

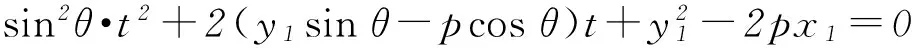
所以

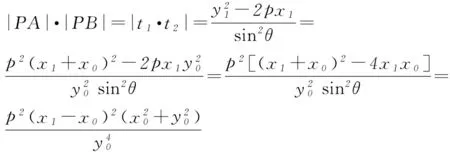
因为点P(x1,y1)在切线l上,由弦长公式可得

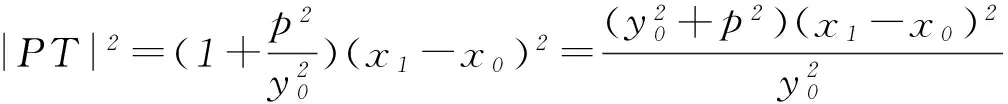
探究至此,深感这道高考题的内涵十分丰富,试题的一般性结论凸显了圆锥曲线的一类切线与割线的内在联系,揭示了该问题的几何本质.