基于相电流正负序分量相角差的高精度内置式永磁同步电机转子初始位置检测方法
2017-01-03刘景林鲁家栋
刘景林 鲁家栋
(西北工业大学自动化学院 西安 710129)
基于相电流正负序分量相角差的高精度内置式永磁同步电机转子初始位置检测方法
刘景林 鲁家栋
(西北工业大学自动化学院 西安 710129)
对内置式永磁同步电机(IPMSM)转子静止初始位置检测技术进行研究,提出一种基于高频信号注入法的高精度IPMSM初始位置检测方法。该方法通过向电机绕组中注入高频旋转电压信号,通过带通滤波器得到高频电流响应,利用同步旋转坐标变换将高频电流响应的正、负序分量进行分离;然后分别对三相高频电流正、负序分量的相角进行最小二乘估计,利用任意一相高频电流正、负序分量的相角差提取出转子的位置信息;最后通过磁路饱和效应对转子N、S极性进行辨别。该方法具有较高的检测准确度,平均检测误差约为1.73°电角度,对一台11 kW的内置式永磁同步电机的实验表明了该方法的正确性。
内置式永磁同步电机 转子初始位置 高频信号注入 最小二乘拟合
0 引言
永磁同步电机不具备自起动能力,在永磁同步电机变频起动过程中,若无法得知电机转子的初始位置,就可能会出现电机转子短暂的“反转”现象,或者在更严重的情况下,电机将起动失败[1-6]。为了使永磁同步电机能够平稳地进行起动,就需要预先得知电机转子的初始位置角θ。传统方法是借助特定的传感器来实现这一位置检测功能,但这势必要增加系统的成本和复杂度,而且也会降低系统的可靠性。
针对上述问题,国内外众多学者对永磁同步电机无位置传感器控制技术进行了大量研究,主要的思想是利用电机绕组中的有关电信号,通过一定的方法估计电机转子位置角[7-10]。其中有一类方法是基于电机转子凸极追踪思想实现的,其代表性方法有高频信号注入法等,由于这种方法利用了电机转子的空间凸极效应,因而适用于具有一定凸极性的电机[6,7,11-15]。利用高频信号注入法估计电机转子初始位置,绕组高频电流响应信号中含有转子的位置信息,但是对高频电流响应信号的解调算法往往比较复杂,运算量大,理论性强,实际应用问题可能较多。文献[1]利用注入高频信号导致永磁同步电机的d、q轴磁路饱和程度不同的原理,实现了其转子初始位置检测,同时根据定子铁心的非线性磁化特性判断转子N、S极性,但是该方法需要估算电机的阻抗特性,方法复杂。文献[6]通过对高频电流响应信号进行解调、滤波和最小二乘拟合处理后,再计算出正弦化响应电流最大值时对应的相位,从而获取转子初始位置角,最后利用磁路饱和凸极效应区分转子N、S极性。文献[11]提出了一种基于三相高频电流响应幅值随转子位置角不同而变化的转子初始位置检测方法,该方法具有对电机参数变化不敏感、算法简单等优点,但是其检测误差限为6°,平均检测误差为2.97°。文献[12]分析了永磁同步电机系统各参数对脉振高频信号注入法位置估计误差的影响,有针对性地减小了位置估计误差。
本文提出了一种基于高频信号注入法的高精度内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor,IPMSM)转子初始位置检测方法,该方法具有较高的位置检测准确度,平均检测误差约为1.73°电角度(下文未专门指出的角度均指电角度),完全能够满足内置式永磁同步电机平稳起动的要求,工程实用价值较高。
1 转子d轴初始位置检测原理
内置式永磁同步电机在两相静止坐标系αβ中的电压、磁链方程为
(1)
(2)
式中,uα、uβ和iα、iβ分别为两相静止坐标系αβ中电机的电压和电流;R为定子电阻;d/dt为对时间t的微分;ψα、ψβ分别为两相静止坐标系下的电机绕组全磁链;ω为电机转子角速度;ψf为永磁体励磁磁链;θ为电机转子位置角度;L0为均值电感,L0=(Ld+Lq)/2;L2为半差电感,L2=(Ld-Lq)/2;Ld、Lq分别为永磁同步电机直轴、交轴电感,且有
(3)
对于式(1),由于初始位置检测时电机处于静止状态(ω=0),并且由于电机绕组中通入高频电压信号,对高频电流分量的分析可以忽略定子电阻压降的影响,因此,忽略等式右侧第1、3项,可得IPMSM的高频电压方程为
(4)
式中,uαh、uβh和iαh、iβh分别为两相静止坐标系αβ中的高频电压和电流。
由于向电机绕组中注入的高频旋转电压信号在两相静止坐标系中的方程为
(5)
式中,U和ωh分别为注入高频旋转电压信号的幅值和电角速度。
利用式(4)、式(5)和2/3变换可得到高频电流响应在三相静止坐标系ABC中的方程为
(6)
(7)
式中,iAh、iBh、iCh分别为三相高频电流响应。
由式(6)可知,A、B、C三相高频电流响应的正、负序分量的相位差均是与转子位置角有关的量。由此可以对三相高频电流正、负序分量进行分离,并通过最小二乘拟合得到各自的相位,通过计算其相位差便可得到转子位置信息。计算方法有:①A相正、负序分量的相位差为转子位置角的2倍;②B相正、负序分量的相位差减去2π/3为转子位置角的2倍;③C相正、负序分量的相位差加上2π/3为转子位置角的2倍;④A、B、C三相各自正、负序分量的相位差之和为转子位置角的6倍。
可以使用上述任意一种方法对转子位置角进行估计。考虑到实际应用时的软件开销问题,可以仅对其中任意一相的电流正、负序分量进行分析来估计转子的初始位置。而通过实验验证,采用上述4种方法中的任意一种对转子位置进行估计,其差异很小。本文后续内容及实验结论部分的转子位置估计均采用第1种方法得到,即对A相电流的正、负序分量进行分析。上述转子位置估计方法的结构框图如图1所示。
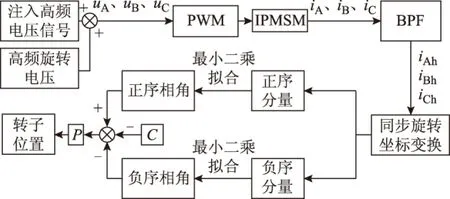
图1 转子位置估计方法结构框图Fig.1 Diagram of rotor position estimation method
图1中,uA、uB、uC分别为注入电机的三相电压值;PWM表示通过三相桥式逆变器将三相电压注入到电机中;iA、iB、iC分别为电机的三相电流响应;BPF(band-pass filter)为数字带通滤波器;C为不同位置估计方法所需要补偿的常数值;P为不同估计方法需要乘(除)的系数。
同步旋转坐标变换的原理与三相静止到两相旋转坐标变换(3r/2s)的原理类似,只是由于此时电机转子位置未知,因而需要假定一个旋转角进行辅助变换。先假定一个与正向分量转向、角速度相同的旋转角θ′和与之对应的d′q′轴系,利用3r/2s对三相高频电流响应进行坐标变换,得到正、负序分量在这个假定d′q′坐标系中的投影,变换方法为
(8)
由于正序分量与假定旋转角θ′是同向同速旋转的,因而正序分量投影到假定d′q′坐标系中的d′、q′坐标轴分量均是直流分量。而负序分量与假定旋转角θ′是反向同速旋转的,因而负序分量投影到假定d′q′坐标系中的d′、q′坐标轴分量均是交流分量。利用低通滤波器可以滤除掉变换后的负序d′、q′轴分量(交流量),再经过反坐标变换就可以得到正序分量;反之,利用高通滤波器可以滤除掉变换后的正序d′、q′轴分量(直流量),再经过反坐标变换就可以得到负序分量。
利用最小二乘算法估计正序分量采样点中某一点处的相角(负序分量相角估计方法与正序分量类似),首先假设正序分量在该点处相角为φ,正序分量在该采样点处的幅值为AMP,信号采样角速度为ωs(已知),正序分量的采样值y[n](n=0,1,2,…)可以表示为
(9)
式中,对每一个确定的n值,cos[2π(ωh/ωs)n]和sin[2π(ωh/ωs)n]均是常数,分别设为Q1[n]、Q2[n]。再做变量替换,设α1=AMP cosφ,α2=AMP sinφ,可以得到
y[n]=Q1[n]·α1-Q2[n]·α2
(10)
对式(10)采用最小二乘算法估计出α1、α2,然后利用α1、α2与正序分量在该点处相角的关系求得φ值。以3点的最小二乘算法为例,这种位置估计算法需要约10次乘法和5次加法的运算量,计算量不大。
2 N、S极性辨别
确定电机转子d轴初始位置后需要对转子N、S极性进行辨别。一般情况下,考虑到电机的材料利用率,在设计电机时往往会让电机磁路处于微饱和的状态,对电机N极正方向施加电压,会增加磁路的饱和程度,从而降低Ld;对电机S极正方向施加电压,会减弱磁路的饱和程度,从而增加Ld。通过计算可知电机d轴电流表达式为
(11)
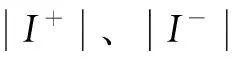

图2 转子N、S极性辨别方法Fig.2 Rotor N,S polarity discrimination method
3 实验与结果分析
为了验证本文所提出的IPMSM转子初始位置检测方法的正确性,在一台IPMSM上进行了实验验证。实验用电机参数见表1。实验中向IPMSM注入的高频电压信号频率为0.5 kHz,幅值为50 V。
表1 实验用IPMSM主要参数
Tab.1 Main parameters of experimental IPMSM

参数数值额定功率/kW11额定电压/V380极对数3d轴电感/mH4.21q轴电感/mH10.09定子电阻/Ω0.179
图3为当转子位置角θ=0°时通过对三相电流响应进行滤波处理后得到的三相高频电流波形。

图3 θ=0°时三相高频电流波形Fig.3 Three-phase high-frequency current when θ=0°
图4为当转子位置角θ=0°时,通过同步旋转坐标变换得到的三相高频电流的正、负序分量波形,其中上标“+”、“-”分别表示正序、负序分量。
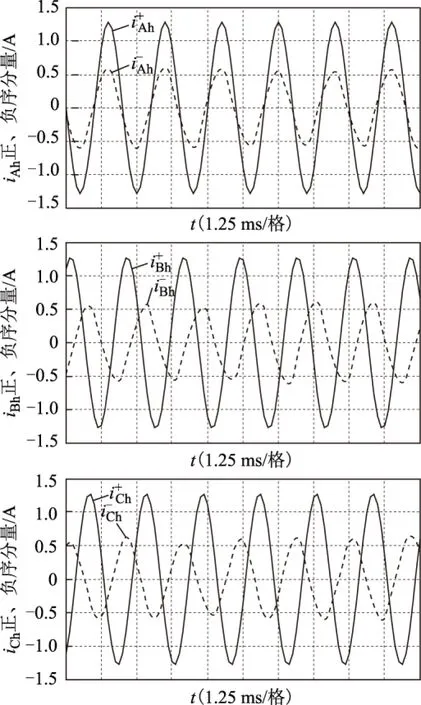
图4 θ=0°时三相高频电流正、负序分量波形Fig.4 Positive and negative sequence component waveform of three-phase high-frequency current when θ=0°
图5为当转子位置角θ=0°时通过最小二乘拟合得到的三相高频电流正、负序分量的相角波形。
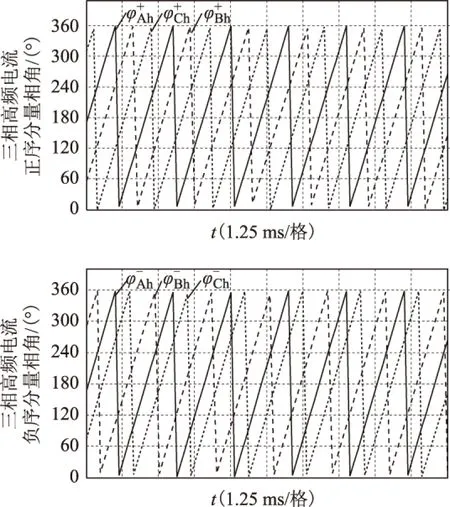
图5 θ=0°时三相高频电流正、负序分量相角波形Fig.5 Positive and negative sequence component phase waveform of three-phase high-frequency current when θ=0°
经过运算可得检测转子位置角θ″=0.19°,经判断,此θ″指向N极位置,因此检测位置角θ′=θ″=0.19°,检测误差Δθ=θ′-θ=0.19°。
图6为当转子位置角θ=210°时的三相高频电流波形。

图6 θ=210°时三相高频电流波形Fig.6 Three-phase high-frequency current when θ=210°
图7为当转子位置角θ=210°时的三相高频电流的正、负序分量波形。图8为当转子位置角θ=210°时的三相高频电流正、负序分量的相角波形。


图7 θ=210°时三相高频电流正、负序分量波形Fig.7 Positive and negative sequence component waveform of three-phase high-frequency current when θ=210°

图8 θ=210°时三相高频电流正、负序分量相角波形Fig.8 Positive and negative sequence component phase waveform of three-phase high-frequency current when θ=210°
经过运算可得检测转子位置角θ″=28.534°,经N、S极性判断可知,此θ″指向S极位置,转子N极位置与检测到的位置角θ″相差180°,因此,最终检测位置角θ′=θ″+180°=208.534°,检测误差Δθ=θ′-θ=-1.466°。
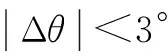
(12)

图9 转子位置检测误差Fig.9 Detection error of rotor position
上述IPMSM转子初始位置检测方法的检测误差主要来源于电流采样误差、电机结构不对称所带来的电流响应误差、数学模型近似所带来的误差等。对于电流响应或检测带来的误差,可以采用增加注入高频信号周期数的方法来尽量减小这一误差。
4 结论
1)本文对内置式永磁同步电机转子初始位置检测方法进行了研究,提出一种基于高频信号注入法的检测技术。通过向IPMSM中注入一个旋转高频电压信号,检测电机绕组的电流响应,并通过BPF滤除杂波得到三相高频电流响应;然后利用同步旋转坐标变换对三相高频电流的正、负序分量进行分离,并通过最小二乘拟合算法估计出三相高频电流的正、负序分量的相角,再通过一定的数学运算得到转子d轴初始位置;最后利用磁路饱和效应对转子N、S极性进行辨别。
2)本文方法不受注入高频电压信号幅值U和角频率ωh的影响,对电机参数变化不敏感,鲁棒性强,转子初始位置检测误差绝对值|Δθ|< 4°,平均检测误差约为1.73°。与现在多数无位置检测技术对初始位置检测问题所能达到的5°的误差,本文方法有一定程度上的提高。整个检测过程用时为ms级,计算量也与一般的高频信号注入法相当,由于初始位置检测问题对检测方法没有很强的实时性要求,因而ms级的检测时间对控制系统和人而言是可以接受的。该方法完全能够满足内置式永磁同步电机平稳起动的要求,工程实用价值较高。
[1] 贾洪平,贺益康.基于高频注入法的永磁同步电动机转子初始位置检测研究[J].中国电机工程学报,2007,27(15):15-20. Jia Hongping,He Yikang.Study on inspection of the initial rotor position of a PMSM based on high-frequency signal injection[J].Proceedings of the CSEE,2007,27(15):15-20.
[2] Diaz R D,Briz F,Blanco C C,et al.Sensorless control of doubly fed induction generators based on rotor high-frequency signal injection[J].IEEE Transactions on Industry Applications,2013,49(6):2593-2601.
[3] 刘家曦,李立毅,杜鹏程.考虑磁场交叉耦合的内嵌式永磁同步电机初始位置检测技术[J].电工技术学报,2013,28(7):32-38. Liu Jiaxi,Li Liyi,Du Pengcheng.Initial rotor position estimation considering magnetic cross-coupling based on IPMSM[J].Transactions of China Electrotechnical Society,2013,28(7):32-38.
[4] 汤宁平,崔彬.高分辨的永磁无刷直流电机转子零初始位置检测方法[J].电工技术学报,2013,28(10):90-96. Tang Ningping,Cui Bin.A high resolution detecting method for rotor zero initial position of sensorless brushless DC motor[J].Transactions of China Electrotechnical Society,2013,28(10):90-96.
[5] 陈思溢,皮佑国.基于滑模观测器与滑模控制器的永磁同步电机无位置传感器控制[J].电工技术学报,2016,31(12):108-117. Chen Siyi,Pi Youguo.Position sensorless control for permanent magnet synchronous motor based on sliding mode observer and sliding mode controller[J].Transactions of China Electrotechnical Society,2016,31(12):108-117.
[6] 王冉珺,刘恩海.永磁同步电机转子初始位置的检测方法[J].电机与控制学报,2012,16(1):62-66. Wang Ranjun,Liu Enhai.Method for initial rotor position inspection on of PMSM[J].Electric Machines and Control,2012,16(1):62-66.
[7] Alberti L,Bianchi N,Morandin M,et al.Finite-element analysis of electrical machines for sensorless drives with high-frequency signal injection[J].IEEE Transactions on Industry Applications,2014,50(3):1871-1879.
[8] 黄科元,周李泽,周滔滔,等.一种增强可靠性的永磁同步电机初始角检测[J].电工技术学报,2015,30(1):45-51. Huang Keyuan,Zhou Lize,Zhou Taotao,et al.An enhanced reliability method for initial angle detection on surface mounted permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2015,30(1):45-51.
[9] 李旭春,张鹏,严乐阳,等.具有参数辨识的永磁同步电机无位置传感器控制[J].电工技术学报,2016,31(14):139-147,164. Li Xuchun,Zhang Peng,Yan Leyang,et al.Sensorless control of permanent magnet synchronous motor with online parameter identification[J].Transactions of China Electrotechnical Society,2016,31(14):139-147,164.
[10]Lin T C,Zhu Z Q.Sensorless operation capability of surface-mounted permanent-magnet machine based on high-frequency signal injection methods[J].IEEE Transactions on Industry Applications,2015,51(3):2161-2171.
[11]鲁家栋,刘景林,卫丽超.永磁同步电机初始位置检测方法[J].电工技术学报,2015,30(7):105-111. Lu Jiadong,Liu Jinglin,Wei Lichao.Estimation of the initial rotor position for permagent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2015,30(7):105-111.
[12]刘海东,周波,郭鸿浩,等.脉振高频信号注入法误差分析[J].电工技术学报,2015,30(6):38-44. Liu Haidong,Zhou Bo,Guo Honghao,et al.Error analysis of high frequency pulsating signal injection method[J].Transactions of China Electrotechnical Society,2015,30(6):38-44.
[13]田兵,安群涛,孙东阳,等.基于磁饱和效应的表贴式永磁同步电机初始位置检测方法[J].电工技术学报,2016,31(1):155-164. Tian Bing,An Quntao,Sun Dongyang,et al.Initial position estimation for surface permanent magnet synchronous motors based on magnetic saturation effect[J].Transactions of China Electrotechnical Society,2016,31(1):155-164.
[14]Reigosa D,Briz F,Blanco C,et al.Sensorless control of doubly fed induction generators based on stator high-frequency signal injection[J].IEEE Transactions on Industry Applications,2014,50(5):3382-3391.
[15]Yu Chen-Yen,Tamura J,Reigosa D,et al.Position self-sensing evaluation of a FI-IPMSM based on high-frequency signal injection methods[J].IEEE Transactions on Industry Applications,2013,49(2):880-888.
High-Precision Estimation Method of Initial Rotor Position for IPMSM Based on Phase Difference of Positive and Negative Sequence Current Component
Liu Jinglin Lu Jiadong
(School of Automation Northwestern Polytechnical University Xi’an 710129 China)
On the basis of the research on static initial position detection technology of interior permanent magnet synchronous motor (IPMSM),a new high-precision method based on high-frequency signal injection is suggested.In the proposed method,a high-frequency rotating voltage was superimposed in the control voltage first,then the high-frequency current component was obtained by band-pass filtering of the three-phase current signal,and the positive and negative sequence components of high-frequency current response were separated by using synchronous rotating coordinate transformation,the phase of positive and negative sequence components of the three-phase high-frequency current response was extracted by the least square algorithm,the rotor position was obtained by using the difference of arbitrary phase current of positive and negative sequence components phase.Finally the NS poles was distinguished by using motor magnetic saturation effect.The method has high-precision detection accuracy,and the average detection error is about 1.73 degrees (electric angle).The experimental results show the correctness of the proposed method.
Interior permanent magnet synchronous motor,initial rotor position,high-frequency signal injection,least square algorithm
陕西省科技统筹创新工程计划项目资助(2013KTCQ01-20,2016KTCQ01-49)。
2015-08-29 改稿日期 2015-10-22
TM315
刘景林 男,1964年生,教授,博士生导师,研究方向为航空航天微特电机及驱动系统、电机智能控制及测试技术等。
E-mail:JinglinL@nwpu.edu.cn
鲁家栋 男,1990年生,博士研究生,研究方向为永磁同步电机无位置传感器控制技术等。
E-mail:310770952@qq.com(通信作者)
