晶体弹性行为的晶体相场模拟*

叶　里，黄礼琳，孔令一，卢强华，高英俊

(广西大学物理科学与工程技术学院，广西高校新能源材料及相关技术重点实验室，广西南宁　530004)



晶体弹性行为的晶体相场模拟*

叶里，黄礼琳，孔令一，卢强华，高英俊**

(广西大学物理科学与工程技术学院，广西高校新能源材料及相关技术重点实验室，广西南宁530004)

(Guangxi Colleges and Universities Key Laboratory of Novel Energy Materials and Related Technology,School of Physical Science and Technology,Guangxi University,Nanning,Guangxi,530004,China)

摘要：【目的】研究晶体相场模型中的弹性相互作用过程。【方法】通过连续的密度场，采用晶体相场模型提取和跟踪每个原子在时间演化过程中的位置，再通过求解PFC方程，并运用原子的位移来构建晶体的弹性能。最后通过调优波动参量和阻尼参数β，获得晶体的弹性及粘弹性行为特征。【结果】当β=0.9时，在力F的作用下，晶体响应是有弹性的。位置距离越远，其对应的应变越大，位移变化与原子对应位置大致成正比，具有弹性关系；当β=9时，在力F的作用下，位移变化与原子对应位置服从粘弹性响应关系。通过调优波动参量和阻尼参数，获得晶体的弹性及粘弹性行为特征。【结论】改变阻尼参数β后，可以采用晶体相场模型模拟晶体的弹性及粘弹性行为。

关键词：晶体相场模拟实验位移弹性

0　引言

【研究意义】纳米晶体材料是近年材料学方面的研究热点，它具有良好的形变特性，因此其形变机理引起了人们的广泛重视[1]。要深入研究材料的变形及其特性与机理，需要把宏观分析与微纳观分析结合起来，在更深的层次上找到其变形机制[2]。现在，对材料变形的研究早已深入到微纳观层次。纳米级微裂纹的形核与扩展在金属材料微观缺陷中普遍存在，并严重降低了金属材料的使用寿命[3]，因此，研究纳米级裂纹的萌生和扩展对预防材料的断裂，提高材料的使用寿命具有重要意义[4]。【前人研究进展】近几年，基于密度泛函理论建立的晶体相场方法(PFC)[5]，能很好地用于描述晶界和位错在扩散时间尺度下的运动特征[6]，可以用于模拟纳米级的微观结构和演化过程[6-8]，并用于研究晶体弹性及粘弹性行为。【本研究切入点】在当前的实验测量条件下，对材料的纳米级行为很难原位观测[9]，因此，发挥计算模拟实验的优势，应用其研究微纳米尺度的结构就显得极为迫切和重要[10-12]。【拟解决的关键问题】应用PFC方法模拟材料弹塑性变形，揭示该过程的原子位移运动特征，研究材料的微结构和弹性及粘弹性行为特征。

1　PFC模型与方法

1.1PFC模型

PFC模型系统无量纲的自由能函数可以写成[8]

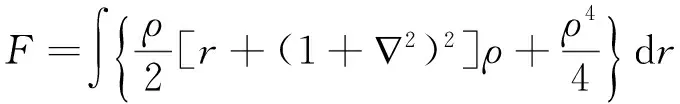
(1)

式中，ρ为局域原子密度；r为与温度有关的唯象参数；2为拉普拉斯算子。在单模近似下，可以求得式子(1)的一个稳定特解

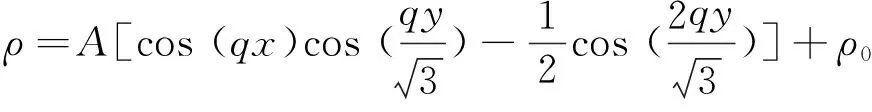
(2)

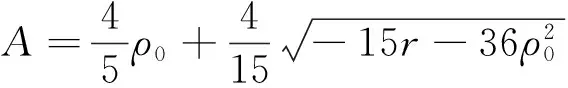
1.2动力学方程

采用保守场Cahn-Hilliard动力学方程[13]描述原子密度随时间的演化。该方程具体表示如下：

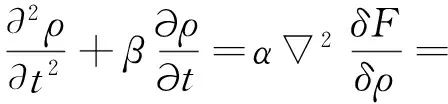
(3)

式中，ρ为局域原子密度，r为与温度有关的唯象参数，表征体系的过冷度。2为拉普拉斯算子，t为时间变量。α是一个运动的参量，β是一个可调的阻尼参数。

1.3数值计算方法

对无量纲动力学演化方程(3)采用二次半隐式傅里叶伪谱方法[14]求解，其离散形式为

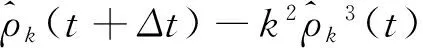
(4)

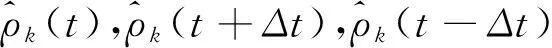
1.4样品制备与应变施加

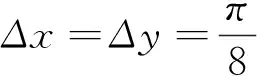
图1初始样品的二维图

Fig.1Two dimensional diagram of initial sample

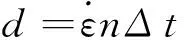
图2沿x轴方向施加拉应变的示意图

Fig.2Schematic diagram of tensile strain applied along x axis

表1不同的样品模拟参数

Table 1Simulation parameters of different samples

样品Samplerρ0ΔtαβA-0.40.310.001150.9B-0.40.310.001159

2　结果与分析

2.1弹性模拟样品

由图3可见：1)当t=120 000时，对应图3a，大约2/3处位移为0，从右往左，位移慢慢增加，应变随之增加，位移从0变化到4，最大位移为4，对应图4中曲线1。2)当t=140 000，对应图3b，位移从0增到5，最大位移为5，对应图4中曲线2。3)当t=160 000时，对应图3c，位移从0变化到6，最大位移为6，对应图4中曲线3。由图4可知：位移随原子位置增加而减小。综上所述，当β=0.9时，随着力F的施加，位置变化小，位移变化也小，位置变化大，位移也相应变大，位置越远，应变越大，位移和位置成正比关系，形成弹性响应关系，晶体响应是有弹性的。

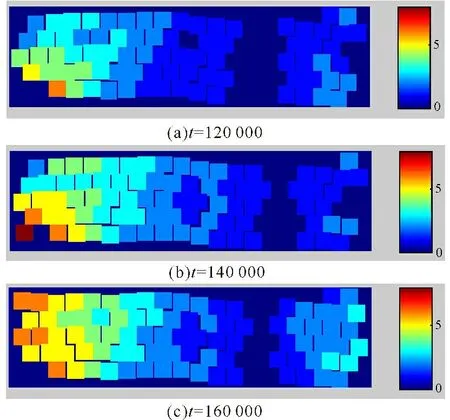
图3弹性模拟样品不同时刻原子位置与相对应的位移

Fig.3Atomic position and relative displacement at different moments of elastic sample

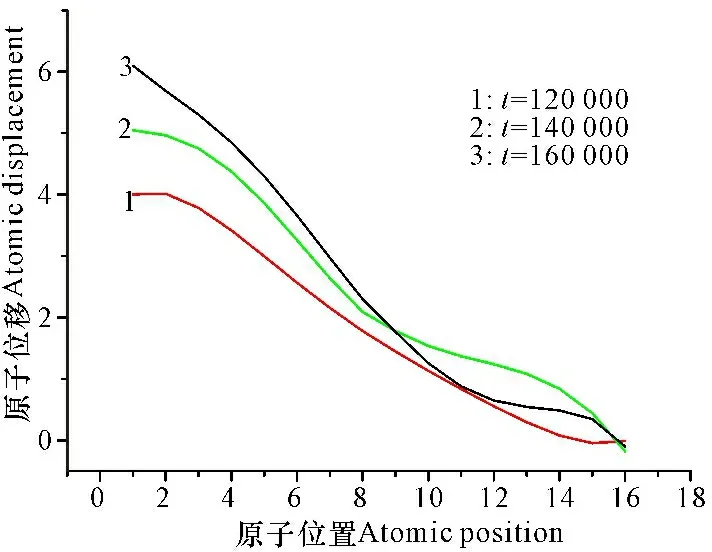
图4不同时刻的原子位置和位移关系曲线

Fig.4The atomic positions and displacement curves at different times

2.2粘弹性模拟样品

由图5可见：1)当t=120 000时，从右到左，位移缓慢增加，位移从0变化到3，最大位移为3，对应图6中曲线1。2)当t=140 000，对应图5b，位移从0增到4，最大位移为4，对应图6中曲线2。3)当t=160 000时，对应图5c，位移从0变化到7，最大位移为7，对应图6中曲线3。由图6可知，位移随原子位置增加而减小，但在位置3处，出现转折变化。综上所述，当β=9时，随着力F的施加，刚开始时，位置变化小，位移变化也小且几乎不变，当该变量达到一定程度，位移有一个跃迁的过程，位移变化相应也大，曲线类似于折线。β从0.9增加到9导致晶体出现粘弹性行为，形成粘弹性响应关系。

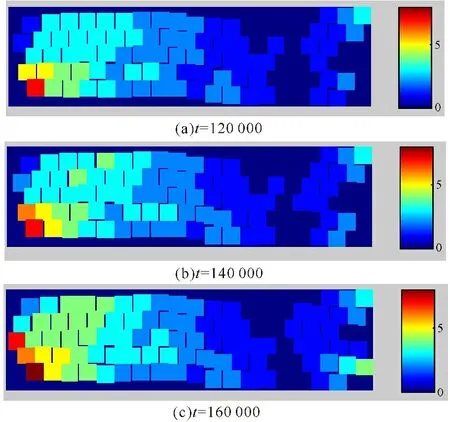
图5粘弹性模拟样品不同时刻原子位置与相对应的位移

Fig.5Atomic position and relative displacement at different moments of viscoelastic sample

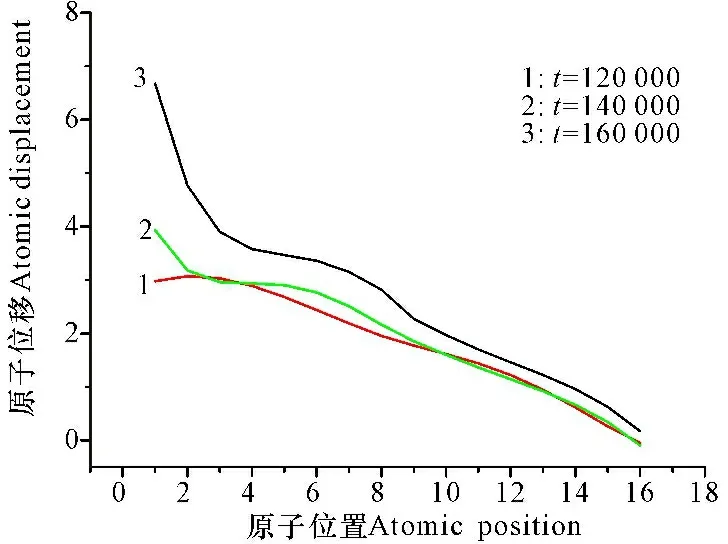
图6不同时刻的原子位置和位移关系曲线

Fig.6The atomic positions and displacement curves at different times

3　结论

应用PFC模型模拟研究材料弹塑性变形，得到如下结论：1)当β=0.9时，在力F的作用下，此时晶体响应是有弹性的。位置距离越远，其对应的应变越大，位移变化与原子对应位置大致成正比，具有弹性关系；2)当β=9时，在力F的作用下，位移变化与原子对应位置关系不服从弹性关系而是服从粘弹性响应关系。表明改变阻尼参数β后，可以采用晶体相场模型模拟晶体的弹性及粘弹性行为。

参考文献:

[1]秦河林,陈建灵,黄世叶,等.外应力作用下小角晶界的斜排位错运动研究[J].广西科学,2015,22(5):506-510,516. QIN H L,CHEN J L,HUANG S Y,et al.Inclined dislocation motion of low angle grain boundaries under shear force exerting[J].Guangxi Sciences,2015,22(5):506-510,516.

[2]邵宇飞,王绍青.基于准连续介质方法模拟纳米多晶体Ni中裂纹的扩展[J].物理学报,2010,59(10):7258-7265. SHAO Y F,WANG S Q.Quasicontinuum simulation of crack propagation in nanocrystalline Ni[J].Acta Physica Sinica,2010,59(10):7258-7265.

[3]LOEHNERT S,PRANGE C,WRIGGERS P.Error controlled adaptive multiscale XFEM simulation of cracks[J].International Journal of Fracture,2012,178(1/2):147-156.

[4]COLOMBO D,MASSIN P.Fast and robust level set update for 3D non-planar X-FEM crack propagation modelling[J].Computer Methods in Applied Mechanics and Engineering,2011,200(25/26/27/28):2160-2180.

[5]ELDER K R,GRANT M.Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J].Physical Review E,2004,70(5):051605.

[6]刘晓骅,叶里,温振川,等.向错强度与阻尼系数对纳米晶材料小角度晶界湮没的影响[J].广西科学,2015,22(5):511-516. LIU X H,YE L,WEN Z C,et al.Influence of disclination strength and damping coefficient on decay of low angle grain boundaries in nanocrystalline materials[J].Guangxi Sciences,2015,22(5):511-516.

[7]毛鸿,罗志荣,黄世叶,等.材料裂纹扩展分叉机理的晶体相场法研究[J].广西科学,2015,22(5):499-505. MAO H,LUO Z R,HUANG S Y,et al.Phase-field-crystal modeling for crack propagation and branch of materials[J].Guangxi Sciences,2015,22(5):499-505.

[8]高英俊,罗志荣,邓芊芊,等.韧性材料的微裂纹扩展与分叉的晶体相场模拟[J].计算物理,2014,31(4):471-478. GAO Y J,LUO Z R,DENG Q Q,et al.Phase-field-crystal modeling of microcrack propagation and branching in ductile materials[J].Chinese Journal of Computational Physics,2014,31(4):471-478.

[9]ARAFIN M A,SZPUNAR J A.A new understanding of intergranular stress corrosion cracking resistance of pipeline steel through grain boundary character and crystallographic texture studies[J].Corrosion Science,2009,51(1):119-128.

[10]CADINI F,ZIO E,AVRAM D.Monte Carlo-based filtering for fatigue crack growth estimation[J].Probabilistic Engineering Mechanics,2009,24(3):367-373.

[11]刘晓波,徐庆军,刘剑.铝裂纹扩展行为的分子动力学模拟[J].中国有色金属学报,2014,24(6):1408-1413. LIU X B,XU Q J,LIU J.Molecular dynamics simulation of crack propagation behavior of aluminum[J].The Chinese Journal of Nonferrous Metals,2014,24(6):1408-1413.

[12]MA L,XIAO S F,DENG H Q,et al.Molecular dynamics simulation of fatigue crack propagation in bcc iron under cyclic loading[J].International Journal of Fatigue,2014,68:253-259.

[13]STEFANOVIC P,HAATAJA M,PROVATAS N. Phase-field crystals with elastic interactions[J].Physical Review Letters,2006,96(22):225504.

[14]BERNAL F,BACKOFEN R,VOIGT A.Elastic interactions in phase-field crystal models:Numerics and postprocessing[J].International Journal of Materials Research,2010,101(4):467-472.

(责任编辑：陆雁)

Phase-field-crystal Simulation for Elastic Behavior of Crystals

YE Li，HUANG Lilin，KONG Lingyi，LU Qianghua，GAO Yingjun

Key words：phase-field-crystal，simulation experiment，displacement，elasticity

Abstract：【Objective】Simulation experiments are conducted in phase-field-crystal (PFC) model to analyze elastic interaction.【Methods】Through the continuous density field,the phase field model is used to extract and track the position of each atom in the time evolution.The PFC method is used to solve the equation,and the atomic displacements are used to construct the crystal elastic energy.【Results】When β=0.9,the crystal response is elastic under the action of force F.The farther away from the position,the larger the strain is,and the change of displacement is roughly proportional to the position of the atom.Under the action of the force F,the change of displacement and the position of the atom correspond to the viscoelastic response when β=9.By tuning wave parameters and damping parameters,the elastic and viscoelastic behaviors of crystals are obtained.【Conclusion】After changing the damping parameter β,the phase-field-crystal model can be used to simulate the elastic and viscoelastic behaviors of crystals.

收稿日期：2016-09-03

作者简介：叶里(1993-)，男，硕士研究生，主要从事金属材料与模拟实验研究。 **通信作者：高英俊(1962-)，男，教授，博士生导师，主要从事材料纳微结构的设计与模拟实验研究，E-mail：gaoyj@gxu.edu.cn。

中图分类号：TG111

文献标识码：A

文章编号：1005-9164(2016)05-0474-04

*国家自然科学基金项目(51161003，50661001)和广西自然科学基金重点项目(2012GXNSFDA053001)资助。

广西科学Guangxi Sciences 2016,23(5):474～477

网络优先数字出版时间：2016-11-21【DOI】10.13656/j.cnki.gxkx.20161121.018

网络优先数字出版地址：http://www.cnki.net/kcms/detail/45.1206.G3.20161121.1546.036.html