基于广域测量信号的电力系统稳定器的设计

吴奎，樊东

(西南交通大学电气工程学院，四川 成都 610031)

基于广域测量信号的电力系统稳定器的设计

吴奎，樊东

(西南交通大学电气工程学院，四川 成都 610031)

考虑了广域测量系统中信号传输过程中存在时滞，将控制器的设计分为了基于本地信号和基于广域测量信号两部分，其中基于本地信号的时滞可以忽略，而基于广域测量信号的时滞不能忽略。建立了包含时滞的电力系统模型。运用Lyapunov泛函理论推导出时滞依赖稳定性的判定方法，并使用LMI方法对时滞依赖稳定条件进行判定。最后以两区四机系统为例，说明了所设计的控制器的有效性。

广域测量系统；时滞；线性矩阵不等式；电力系统稳定器

1 引言

在大规模电力系统的发展和快速励磁系统的普遍应用的背景下，电力系统低频振荡的现象在国内外均有发生，这种低频振荡常出现在长距离、重负荷输电线上，在采用现代快速、高顶值倍数励磁系统的条件下更容易发生[1]。电力系统稳定器PSS是目前应用得较为广泛的一种抑制低频振荡的方案[2]。对于本地的低频振荡，电力系统稳定器具有很好的抑制效果，由于电网的区域互联，一些低频振荡不但发生在本地区域，也可能发生在区域之间，这时，基于本地信号的电力系统稳定器就无法对区域间的低频振荡起到较好的抑制效果。随着广域测量系统(WAMS)在电力系统中的应用，使得利用广域信号来抑制低频振荡成为可能[3]。广域测量系统是利用分步在各地的相量测量单元(PMU)实时采集电网运行时的各种数据并打上时标，通过网络将数据传回数据中心[4]。由于广域信号在网络中的传输是有时滞的，并且随着电网规模的扩大，数据传输的时滞不能被忽略。通常，广域测量信号在网络中的传输时滞可达几十毫秒，甚至上百毫秒[5-7]。文献[8-9]使用了LMI方法进行了控制器的设计，但是都没有考虑信号传输时滞的影响。如果直接使用广域测量信号来抑制低频振荡而不考虑时滞的影响，很有可能造成系统不稳定。本文考虑了广域测量信号在网络中的传输时滞，建立了包含时滞的电力系统的模型，并采用Lyapunov理论推导了包含时滞的系统的稳定性，然后基于LMI方法设计出既包含本地信号又包含广域测量信号的广域电力系统稳定器。并在Matlab环境中建立电力系统的模型，对所设计出的广域电力系统稳定器进行仿真试验，以验证其有效性。

2 电力系统建模

区域互联的电力系统在弱联系的情况下进行区域这间相互输送电能的时候，如果受到扰动时，很可能产生低频振荡。为了要抑制这些低频振荡，有必要在电力系统中加入控制器，以增加系统的阻尼，使得低频的振荡能够迅速得到抑制。

为了进行控制的设计，对电力系统进行数学建模是很有必要的。对于一个多机电力系统，系统中包含有n个同步发电机，每个发电机都安装有励磁系统，每个同步发电机都使用实用三阶模型来描述，励磁系统用一阶模型来描述，电力系统的数学模型可以描述成如下形式：

(1)

(2)

式中：E为适维的单位阵；M为发电机的惯性时间常数；D为阻尼系数。

K1=∂Pe/∂δ

K5=∂Ut/∂δ

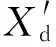
(3)

3 考虑时滞影响的控制器的设计

当互联电力系统中存在低频振荡时，在电力系统中加入传统的电力系统稳定器，能够增加区域内的低频振荡的阻尼比，使区域内的振荡能够得到抑制。但并不能有效的使区域间的振荡快速平息。

基于这些问题，本文所要设计的控制器是由基于本地信号的本地阻尼控制器和基于广域测量信号的阻尼控制器两部分构成。基于本地信号的控制器主要是用于增强区域内的低频振荡的阻尼比，基于广域信号的控制器主要用于增强区域间低频振荡的阻尼比。

其中本地控制器使用的是本地机组的信号，此时信号传输过程中的延时是很小的，可以将其忽略。然而广域控制器使用的是基于WAMS的广域测量信号，这些信号是从很远的地方传输过来的，此时信号传输过程中产生的延时是不能忽略的，在设计广域控制器的时候需要考虑通讯时滞的影响。本文所设计控制器的目标：增强区域内低频振荡和区域间低频振荡的阻尼比，使其能够达到0.1以上，并且能够有较大的时滞裕度，让信号传输的时滞在100ms以上时还能够使系统稳定。

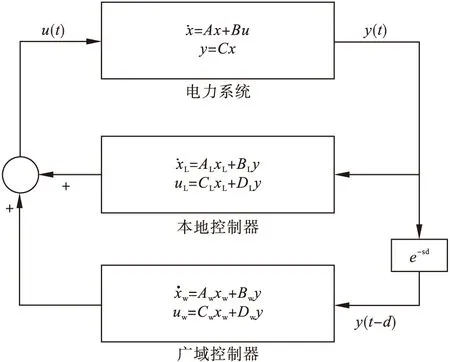
图1 包含广域控制的闭环电力系统

3.1 本地控制器的设计

基于本地信号的控制器的设计跟传统电力系统稳定器的设计方法是一样的。本文所设计的本地控制器使用了本地的同步发电机的转子角速度作为控制器的输入信号，而输出一个电压信号作用在励磁系统上，作为励磁系统的一个附加的输入，将其反馈回本地的同步发电机，从而构成一个闭环控制，抑制本地区域的低频振荡。

图2 本地控制器的传递函数框图

本地控制器的状态方程可表示成如下形式：

(4)

本文所设计的本地控制器的传递函数框图如上图所示，为一个三阶的系统，标准的状态方程形式如下：

(5)

uL=[-abb1][v1v2v3]T+abKΔw

由于本地控制器使用的本地发电机组的信号，信号传输过程中的时滞可以忽略，于是，本地控制器与原来不含控制器的电力系统一起构成了一个不含时滞的电力系统，可是将其表示成如下的状态空间模型

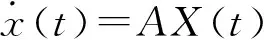
(6)

其中

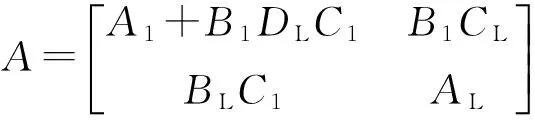
包含本地控制器电力系统的状态向量变为了

3.2 广域控制器的设计

广域控制器的主要结构包含有一个隔直环节和多个超前滞后环节，一般设计为两个超前滞后环节，广域控制器的传递函数可以表示为如下形式：

(7)

广域控制器的状态方程可表示成如下形式：

(8)

由于控制器使用的是广域信号，电力系统的输出信号在传输过程中含有时滞，并且这个时滞是不能被忽略的，在设计控制器的时候，需要将时滞考虑在其中。因此输出反馈信号y(t)y(t-d)用来替换。

将广域控制器加入到电力系统中，形成的闭环控制的模型可以表示成

(9)

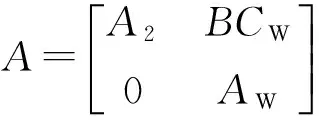
广域控制器在参数的设计上可采用相位补偿法来进行设计。广域控制器所使用的输入信号是含有时滞的，众所周知，时滞对控制系统的稳定性会产生影响。这就需要验证所设计的控制器在某个时滞范围内能否使系统稳定。本文使用了LMI方法来计算时滞系统的稳定裕度，以验证所设计的广域控制器的有效性。下面给出了使用线性矩阵不等式进行时滞依赖稳定性判断的依据。

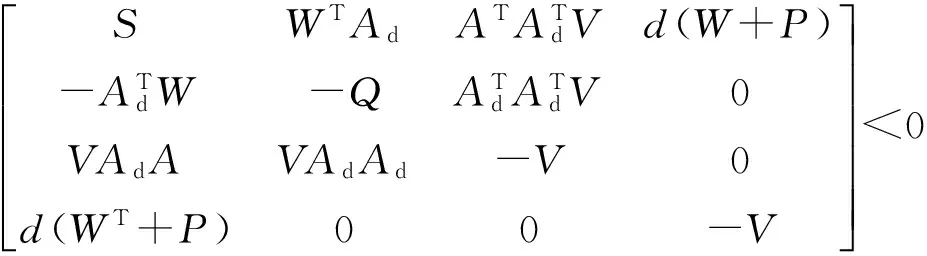
(10)

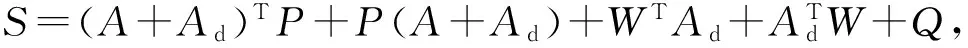
V(x)=V1(x)+V2(x)+V3(x)

(11)

其中：

V1(x)=xT(t)Px(t)

由Newton-Leibniz公式可得

(12)

于是时滞系统方程可以写成

(13)

由此可见，x(t)只要满足(12)，则也满足(13)。可将V1(x)关于时间的导数表示成如下：

(14)

使用一个放大不等式

(15)

可得

(16)

于是，将其代入(14)，可得

(17)

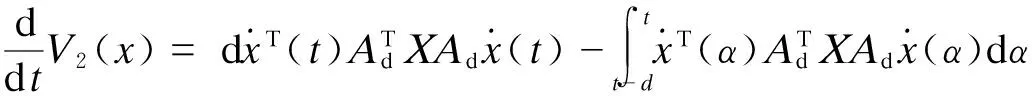
(18)

(19)

于是，V(x)对时间求导的表达式可以表示为

(20)

其中：

W=XMP，V=dX

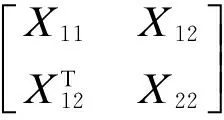
4 仿真算例

为了说明本文方法的有效性，以下给出了一个两区四机系统的算例。该系统是研究电力系统低频振荡问题时使用得较为广泛的一个系统。系统由两个区域组成，两个区域之间通过两条220km长的联络线进行连接。每个区域由两台发电机组成，每台发电机的额定容量为900MVA，额定电压为20kV，四机系统的主要参数使用文献[10]中的参数。由于两个区域的容量比较大，而两个区域之间的联系较弱，在有扰动的情况下很容易引发系统之间的振荡。

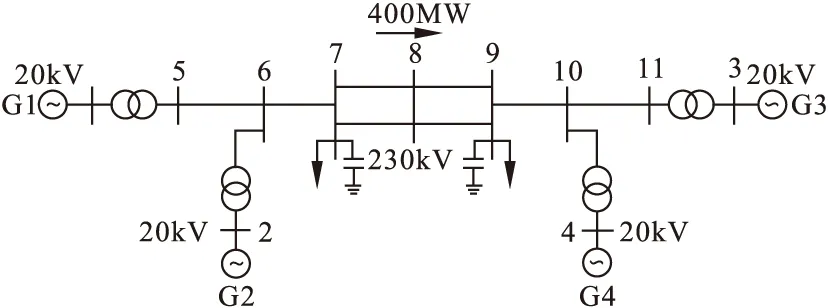
图3 两区四机系统接线图

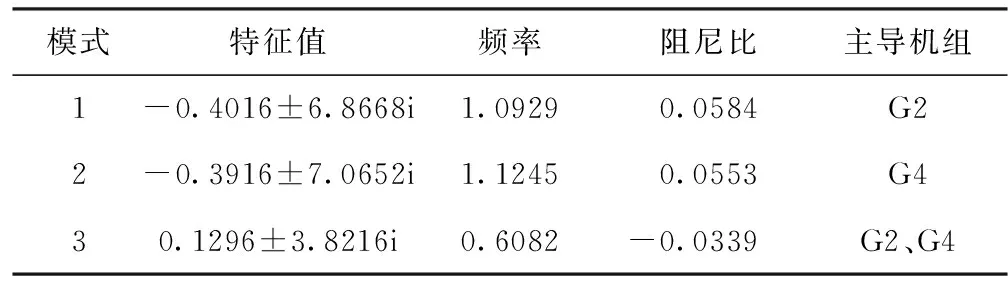
模式特征值频率阻尼比主导机组1-0.4016±6.8668i1.09290.0584G22-0.3916±7.0652i1.12450.0553G430.1296±3.8216i0.6082-0.0339G2、G4

该系统有三个机电振荡模式，分析特征根与状态变量的相关性，可以看出，模式1主要是根发电机G2相关，模式2主要是根发电机G4相关，模式3主要是根发电机G2和G4相关。模型1和模式2是区域内的振荡，模式3是区域间的振荡。其中模式1和模式2的阻尼比较小，模式3为负阻尼，需要增大其阻尼比，以提高系统的稳定性，抑制区域内和区域间的低频振荡。对特征根灵敏度分析，可以确定电力系统稳定器的安装位置，以便更有效的作用于某一个振荡模式。由分析可知在发电机G2和G4上安装控制器对低频振荡的抑制效果最好。

4.1 本地控制器

本地信号在传输过程中的时滞很小，可以将其忽略，所以在设计时可以使用传统的以本地机组的转子角速度作为输入信号的电力系统稳定器的设计方法，配置在G2和G4两台发电机上，以增强本地振荡模式的阻尼。所设计出的本地控制器的传递函数为

系统加上本地控制器以后，本地振荡模式的阻尼比有所加强，达到了0.1以上，满足的设计的要求，区域间振荡模式的阻尼也变为正值，但阻尼较弱，还需要加入广域控制器来提高区间振荡模式的阻尼。

4.2 广域控制器

广域控制器在进行设计时需要考虑到信号传输时滞所带来的影响，需要将时滞稳定裕度作为控制器设计的一项重要指标。使得所设计出来的控制器能够容纳更大的时滞。以下是使用LMI方法验证系统时滞稳定裕度的算法。

(1)给定一个较小的时滞d作为初始值，以确保定理1中的LMI存在可行解。

(2)计算定理1中的LMI。

(3)判断(2)所计算的结果是否为可行解。若存在可行解，记录该时滞d，并将时滞改为d=d+5ms，返回(2)，否则输出前一次所得时滞d。

步骤(3)最后输出的时滞d即为时滞系统最大能容纳的时滞大小，对于系统中时滞信号，只要小于d，时滞系统都可以保持渐近稳定的。

在本文中，以发电机G2与G4的转子角速度差作为广域控制器的输入信号，并以此来设计控制器，设计的时候需要考虑时滞的影响，首先使用相位补偿的方法来设计控制需要补偿的角度，以此来确定控制器中超前环节中T1和T2的值，然后通过LMI求取时滞裕度大小的方法来确定控制器增益大小K，使得时滞系统能够容纳较大的时滞，并且有能提供足够的阻尼。通过计算可以确定出控制器的T1=0.32，T2=0.21。

在控制的设计中，最重要的是确定控制器的增益K，当K取不同值时，时滞系统能够容纳的最大时滞，以及振荡模式的阻尼比的大小都有变化，需要选取既能够容纳较大时滞，又能提供较大阻尼比的K值。

通过计算，当K=10的时候，系统有较大的时滞稳定裕度，同时也使系统有较大的阻尼，将其确定为本控制器的参数。

为了检验所设计的控制器抑制低频振荡的性能，在两区四机系统的联络线上设置一个三相短路故障，并在0.2s后自动重合闸，系统的仿真波形如下图所示。

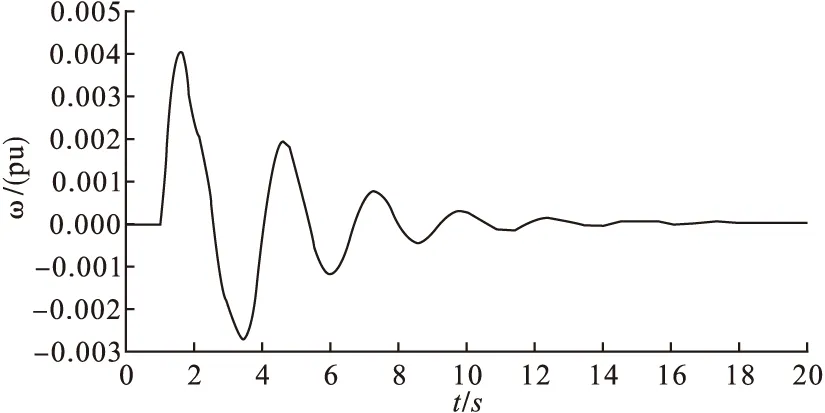
图4 只加入本地控制器时G2和G4角速度差

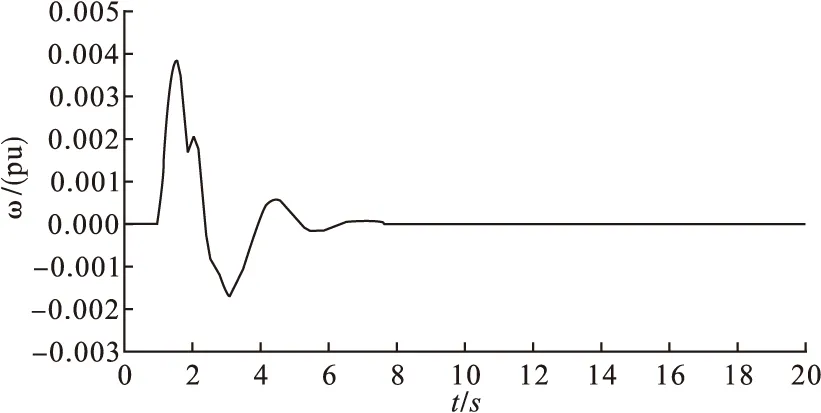
图5 时滞为100ms时加入广域控制器时G2和G4角速度差

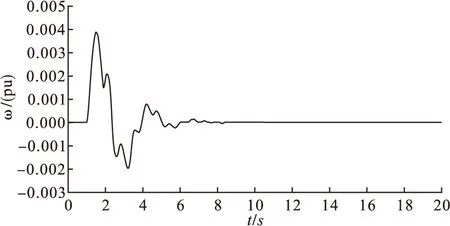
图6 时滞为150ms时加入广域控制器时G2和G4角速度差

由以上的仿真可以看出，系统在所给的100ms，150ms两个不同的信号传输时滞时，广域控制器都能有效的抑制低频振荡，达到了设计的要求。

5 结论

本文考虑了广域信号在传输过程中含有时滞，给出了基于本地信号和基于广域信号的两层控制器的设计思路，使用基于本地信号的控制器来控制区域内的低频振荡，使用基于广域信号的控制器来抑制区域间的低频振荡。建立了包含信号传输时滞的电力系统的模型，运用了基于LMI方法求解时滞依赖稳定性的思路来进行控制器的设计。最后通过两区四机系统的仿真，说明了本文所设计的时滞控制器是有效的。

[1] 倪以信，等.动态电力系统的理论和分析[M].清华大学出版社，2002.

[2] 朱方,汤涌,张东霞,等.我国交流互联电网动态稳定性的研究及解决策略[J].电网技术,2004,28(15):1-5.

[3] Aboul-Ela ME,Sallam AA,McCalley JD,etal.Damping Controller Design for Power System Oseillations Using Global Signals[J].IEEETrans.On Power Systems,1996,11(2):767-773.

[4] D Karlsson,M Hemmingsson,S Lindahl.Wide area system monitoring and control-terminology,phenomenaandsolutionimplementationstrategies.IEEE Power&EnergyMagazine,2004,2(5):68-76

[5] Taylor C W,et al.Wide-area Stability and Voltage Contro1.In:Proceedings of the ⅦSymposium of Specialists in Electric Operational and Expansion Planning,2000,Curitiba,Brazil,Vol.1:1-9.

[6] 胡志祥，谢小荣，肖晋宇,等.广域测量系统的延迟分析及其测试[J].电力系统自动化，2004，28(15)：39-43

[7] B.NADUVATHUPARAMBIL,et al.Communication Delays in Wide Area Measurement Systems.In:Proceedings of the 34th Southeastern Symposium on System Theory,2002,Huntsville,USA,pp:118-122

[8] Tsai H C,Chu Y S.Robust power system stabilizer design for an industrial power system in Taiwan using linear matrix inequality techniques[C].IEEE Power Engineering Society General Meeting,Taiwan,2004.

[9] Chen H,Guo Z.LMI-based wide-area robust damping control[C].IEEE/PES Transmission and Distribution Conference and Exhibition:Asia and Pacific,Dalian,China,2005

[10] Kundur P.Power system stability and control[M].New York:McGraw Hill,1994.

Design of the Power System Stabilizer Based on WAMS

WUKui，FANDong

(School of Electrical Engineering，Southwest Jiaotong University，Chengdu 610031，China)

Considering the existence of time-delay of signal transmission in the WAMS,the controller contain two parts,and one is based on local signal,the other is based on WAMS signal.The transmission delay based on local can be ignored,but the delay based on WAMS should be considered.Establishing the power system model with time-delay.The Lyapunov approach is used to derive a delay-dependent steady criterion.Using LMI approach to judge the steady or not.Finally,using a two-area four-machine power system to show the effectiveness of the controller.

WAMS;time-delay;linear matrix inequality;power system stabilizer

1004-289X(2016)03-0048-06

TM71

B

2015-03-12

吴奎(1987-)，男，硕士研究生，研究方向为电力系统稳定性； 樊东(1989-)，男，硕士研究生，研究方向为电力系统稳定器控制。