变压器励磁涌流的识别方法综述

张小钒，兰生

(福州大学电气工程与自动化学院，福建 福州 350108)

变压器励磁涌流的识别方法综述

张小钒，兰生

(福州大学电气工程与自动化学院，福建 福州 350108)

变压器差动保护动作的正确率一直以来都受到励磁涌流的影响，近年来大量国内外继电保护工作者进行了深入的研究，并提出许多新的励磁涌流识别方法。本文将国内外各文献提出的识别励磁涌流与区内故障电流的方法进行整理归纳，分析总结出各种方法的优缺点及实用性，最后对将来解决励磁涌流问题的研究方向进行了展望。

变压器；励磁涌流；差动保护

1 引言

电力变压器在电力系统中承担着至关重要的作用，是发电厂和变电站中不可或缺的电气设备。电力系统能否正常、稳定的运行，其中一个非常重要的前提是大型变压器要先能正常、稳定的工作。此外，由于大型变压器本身的造价就十分昂贵，若因差动保护装置不能准确、及时的对发生严重内部故障的变压器动作跳闸，导致变压器内部结构严重损坏，经济上也将造成巨大的损失。而且大型变压器损坏后，检修难度大，持续时间长，大范围区域的长时间停电，将给人民的经济带来巨大的损失。因此，必须准确、有效的控制变压器差动保护装置的动作，既不能误动作，也不能拒动作。

变压器差动保护作为变压器的主保护，一直受到励磁涌流问题的困扰，在2002～2006年间，220kV及以上变压器保护的正确动作率仅为81.912%，远不如100MW及以上发电机保护的98.476%[1]。因此，必须提高变压器纵差保护动作的正确率。

近年来，国内外继电器保护工作者进行了大量研究，并取得了一定的进展。文中将各文献提出的识别励磁涌流，以防止差动保护误动作的方法进行整理归纳。通过分析比较各方法的优缺点，指出其实用性，并展望了将来研究解决励磁涌流问题的主要方向。

2 励磁涌流的识别方法

目前，实际现场的变压器差动保护系统，主要采用以差动电流波形特性为依据的二次谐波制动原理和间断角原理来识别励磁涌流。并且，由于二次谐波制动原理因为算法简单，且易于在微机中实现，所以应用得最为广泛，已具有多年的现场运行经验[2]。此外，利用变压器电流量判别励磁涌流的方法还有波形对称原理[3]、积分型波形对称原理[4]、半波叠加制动原理[5]、波形正弦度特征判别法[6]、波形相似原理[7]、波形相关性分析法[8]、波形拟合法[9]、虚拟三次谐波原理[10]和峰—峰间距判别法[11]等。利用变压器电压量判别励磁涌流的方法有低电压制动原理和谐波电压制动原理。综合利用变压器电流量和电压量判别励磁涌流的方法有功率差动原理和基于变压器模型法(包括基于等效瞬时漏电感和基于等值回路方程等)。

随着研究领域不断扩大，研究层次不断深入，许多科研人员将多学科相互结合，从而提出诸多新的励磁涌流识别方法，如：基于神经网络、基于小波变换和基于模糊逻辑算法的变压器励磁涌流识别法。此外还有：基于支持向量机[12]、基于双曲线S变换[13]、基于希尔伯特-黄变换[14]、基于数学形态学[15]的励磁涌流识别法等。这些新方法也为励磁涌流的识别增添了新的思路。

2.1 利用变压器电流量判别励磁涌流

2.1.1 二次谐波制动原理[16-17]

变压器励磁涌流与区内故障电流相比，含有较高的二次谐波分量。利用这一差异性作为励磁涌流的制动判据如式(1)所示：

(1)

式中Id1、Id2分别为差动电流的基波幅值和二次谐波幅值；K为二次谐波制动比，通常取15%～20%。

由于二次谐波制动原理算法简单，并且对微机处理器要求不高，容易在微机中实现，因此在实际差动保护装置中得到了非常广泛的应用。但如今由于制造变压器的铁磁材料不断改进，使得励磁涌流中的二次谐波含量有所降低；另一方面，在高压输电线路中，由于长线路和电缆线分布式电容的存在以及受到电网中日益增多的无功补偿装置的影响，引起区内故障电流的二次谐波含量较以往有所升高，从而二次谐波制动比的取值难以整定，导致传统二次谐波制动原理的正确动作率下降[18]。

又由于为了保证变压器差动保护制动的可靠性，目前对于二次谐波制动系数的整定现场一般采用最大相制动方式(“或”门制动方式)。但当变压器空投于区内故障时，差动保护会因无故障相的励磁涌流制动而延迟动作，在某些情况下延迟将达2s以上，这严重降低了变压器差动保护的速动性。

为了解决传统二次谐波制动原理所面临的困境，近年来已有大量科研人员在原有算法的基础上加以改进。

骆建等[19]利用变压器区内故障电流的基波幅值不衰减，而励磁涌流的基波幅值表现出衰减趋势，在检测到这一特性时，通过设置浮动门槛，适当降低二次谐波制动比，而发生区内故障电流时仍保持高制动比，这样可以进一步提高变压器差动保护系统识别励磁涌流的能力。但该方法在面对和应涌流时将失效，因为和应涌流的基波幅值也长时间不衰减。

袁宇波等[20]研究发现励磁涌流的基波相位与二次谐波相位相差0°或180°。利用这一特性，在相位相差大约为0°或180°时适当降低二次谐波制动比，而在设定的相位范围外仍保持高制动比，这样也进一步提高了变压器差动保护系统识别励磁涌流的能力。虽然该方法在应对和应涌流时，能起到较好自适应效果，但在应对对称性励磁涌流时，由于相位差波动剧烈，不利于实际应用。

若能将上述两种二次谐波自适应方法合理的相结合，组成的变压器差动保护系统在集合两种方法的优点后，适用范围将更加全面。

2.1.2 间断角原理[21]

间断角原理由我国率先提出并应用于现场保护，现已得到广泛的应用。它是利用励磁涌流有很大的间断角，而区内故障电流没有，这一差异性来判别的。其判据如下：

(2)

若间断角θJ>65°，则判定为励磁涌流，闭锁差动保护；若间断角θJ≤65°，且波宽θW≥140°，则判定为非励磁涌流，解锁差动保护，一旦θJ>65°，则立即闭锁差动保护。

其优点是可采用分相制动方式，在空投于变压器区内故障时能迅速跳闸，并且具有一定的过励磁能力。缺点是受电流互感器饱和时引起二次侧波形畸变的影响。当电流互感器进入饱和状态时，差动电流的间断角区域波形会往负值延伸，且电流互感器饱和越严重，延伸程度越大，致使励磁涌流情况下检测不到间断角的存在；而区内故障电流情况下却反而可能由于电流互感器的饱和而产生间断角，这样必然会导致差动保护误动作或拒动作。此外，只有采用很高的采样频率才能准确的测得间断角的值，这就要求使用性能更高的微机处理器。并且，由于励磁涌流间断角区域的电流值处于零点附近，普通精度的A/D转换芯片转换后会产生较大的误差，因此需要使用高精度的A/D转换芯片才能准确转换，这些要求都提高了间断角原理所需的硬件成本。

2.1.3 波形对称度原理[3]

波形对称原理是利用区内故障电流波形基本对称，而励磁涌流一般不对称的特点来判别。将差动电流波形求导后所得波形一周期内的前半波和后半波作对称比较来进行判别。对称度的定义式为：

(3)

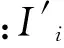
当Ksym≤Kset时认为差动电流波形对称，否则认为不对称。若连续半个周波以上的数值都成立则判定为故障电流，否则判定为非故障电流。

该原理对硬件的要求较低，容易实现，但同样受电流互感器饱和问题和电力系统谐波等原因的影响，很可能使得差动电流波形发生变形，这就使得区分励磁涌流与区内故障电流的对称度系数Kset的取值不能找到明确的边界，Kset的取值难以整定。取得太大，在励磁涌流情况下，可能误动作；而取得太小，在区内故障情况下，又可能拒动作。

另外，区内故障电流也并非时刻都对称，可能在某个时间段受到较大不平衡电流的影响，而使式(3)在发生故障后仍长时间不成立，导致差动保护延迟动作。因此，波形对称原理还需要进一步深入研究。

在波形对称原理的基础上，许多科研工作者相继提出了积分型波形对称原理、半波叠加制动原理、波形正弦度特征判别法、波形相似原理、波形相关性分析法、波形拟合法等等，这些方法其实都是利用励磁涌流和内部故障电流的波形存在某种差异性来判别，其实都是间断角原理的推广。

2.1.4 小结

励磁涌流的大小和持续时间，受下列各种因数的影响：①大电源和变压器之间电力系统的时间常数L/R值，该值越大，励磁涌流衰减越慢；②变压器额定容量的大小，容量较大的变压器L值相对较大；③变压器安装的位置和大电源之间的阻抗值R，安装距离越近，则R值越小；④电力系统容量的大小；⑤变压器选用的铁芯材料以及饱和磁通密度值的大小；⑥加压操作前变压器剩磁的大小；⑦断路器合闸瞬间电压的相位角度[22]。因此，利用变压器差动电流波形特征为依据的励磁涌流识别方法均不能完全保证有100%的正确动作率，差别仅是正确动作率的高低。

2.2 利用变压器电压量判别励磁涌流

2.2.1 低电压制动原理[23]

低电压制动原理提出利用变压器的端口电压作为识别变压器励磁涌流与区内故障电流的辅助判据。当变压器发生励磁涌流时，其端电压不但不会降低，而且还可能升高。而发生接地故障时，故障相电压会变得很小，当相电压低于额定电压的70%时将二次谐波制动判据解锁。但为了防止变压器区外故障清除后产生的电压复原涌流造成保护误动作，在一定条件下闭锁差动保护。

该辅助判据有助于识别变压器接地故障，但如果变压器低压侧安装了无功补偿装置，当发生接地故障时，变压器的端口电压需要等电容器释放大部分电量才会明显下降，这必然会引起变压器保护装置延迟动作。

2.2.2 谐波电压制动原理

在励磁涌流情况下，由于变压器的铁芯严重饱和，导致变压器的输出电压波形发生畸变，因此含有较大的谐波分量，而内部故障时的电压波形谐波含量低，因此可利用这一差异性进行判别。

谐波电压制动原理几乎LC不受振荡的影响，并且采用分相制动方式，挺高了差动保护的速动性。但文献[24]指出该方法与电源阻抗的大小密切相关，必须对系统阻抗值有准确的了解后才能对阀值进行整定。

2.3 差有功法

变压器在正常运行情况下的有功损耗一般小于其额定容量的1%，而在发生励磁涌流情况下，刚开始时会损耗较大的有功转为磁能存储在绕组中，随后进入正常运行状态就变得很小了；而当变压器内部绝缘被击穿时，电弧放电瞬间将会损耗大量有功。因此，可以利用变压器有功损耗的大小，来判别变压器是否正常工作。为了提高保护的灵敏度将铜损耗去除，对于单相双绕组变压器有：

(4)

式中：u1、u2、i1、i2、r1、r2分别为变压器原边和副边绕组的瞬时电压、电流及电阻。

该方法的判据为：若W(t)>ζ，则判定为内部故障，否则认为无故障发生。设置阈值ζ是为了防止采样时延导致电压、电流相位误差，从而引起W(t)误差。

差有功法同时利用了变压器电压量和电流量的信息，能更准确的反应变压器的运行状态。然而，该方法需要避开励磁涌流的第1周波，延迟了判别时间；此外，励磁涌流情况下的铁耗有所增加，并且因为不能准确的计算铜耗，导致难以确定的取值。而且，在外部故障情况下，因为有较大的穿越电流流过变压器，有功损耗明显增大，所以ζ的取值需要躲过变压器外部故障时的最大有功损耗，这样便降低了保护的灵敏度。

马静等[25]在差有功法的基础上，提出将变压器等值回路方程中的非线性项消去，构造出仅含有漏电感和绕组电阻的二端口网络。利用励磁涌流和内部故障情况下输入端口的广义瞬时功率直流分量的大小来判别。古斌等[26]提出一种利用变压器三相差有功功率与差无功功率直流分量比值的大小，来判别励磁涌流和区内故障电流。

2.4 等值回路方程识别法

如图1所示的单相双绕组变压器，有式(5)方程：

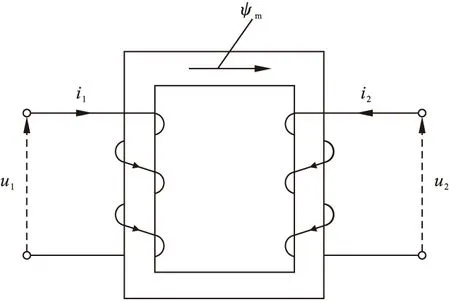
图1 双绕组单相变压器

(5)

式中：u1、u2、i1、i2、r1、r2、L1、L2、ψm分别是变压器原边和副边绕组的瞬时电压、电流、电阻、漏感及互感磁链。设变压器的变比为nT=1。将式(5)中的dψm/dt消去得：

(6)

由于式(6)是根据变压器正常运行时的等效模型求得的，因此在变压器未发生内部故障时都成立，而当发生内部故障时，等效模型产生了变化，式(6)才不再成立。因此，通过判别式(6)是否成立就能知道是否有内部故障发生。此原理不受励磁涌流、过励磁和外部故障情况的影响，但漏感参数L1、L2难以精确计算。

郝治国等[27]也对等值回路方程原理进行了深入的分析，推导出了三相双绕组Y/Y和Y/Δ接法变压器的保护动作方程。马静等[28]利用变压器内部故障时，短路电动力会使绕组变形，导致漏感参数发生变化；而非内部故障时，变压器的漏感参数不会发生变化，利用这一差异性可以有效地判别变压器是否发生内部故障。

2.5 等值参数识别法

Keizo Inagaki等[29]提出通过检测变压器对地等值导纳参数的变化，来判别励磁涌流和内部故障电流。三绕组变压器导纳型等值电路，如图2所示。

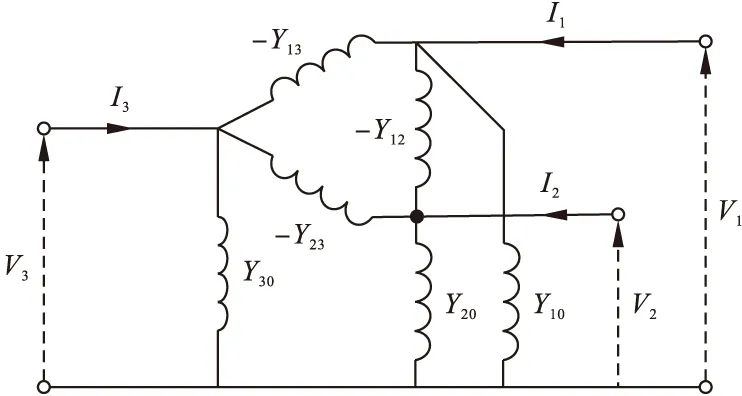
图2 三绕组变压器导纳型等值电路

图中导纳仅Y10、Y20、Y30与变压器运行状态有关，其余无关。

变压器运行状态与各侧对地导纳的关系如表1所示。

表1 对地导纳参数与变压器的运行状态关系

通过表1可设置阀值ξi(i=1，2，3,分别与Y10、Y20、Y30对应)来判别变压器的运行状态，具体取值的整定需要经过试验和分析后才能确定。

该方法的优点是：判别速度快，且不受电流互感器饱和的影响；缺点是：导纳的计算需要使用变压器漏感参数，而漏感参数无法精确求得，致使导纳计算产生误差，另外，ξi也不易整定。

2.6 磁通特性识别法

Phadke A G等[30]提出利用ψ-id曲线(磁链-差动电流曲线)在励磁涌流和区内故障情况下变化的差异性来判别。在励磁涌流情况下，计算得到的ψ-id曲线即为变压器的空载磁化曲线；而在内部故障情况下，ψ-id曲线开始偏离空载磁化曲线，并且故障越严重偏离越远。通过这一特性，可以判别励磁涌流与内部故障电流。但该方法在实际应用中受变压器不确定剩磁的影响，所得到的ψ-id曲线产生了误差，从而导致误判。

为了避开不确定剩磁的影响，文献[30]又做了改进，用斜率dψ/did曲线代替ψ-id曲线来进行判别。但在变压器发生轻微内部故障时，dψ/did的值几乎与正常运行时相等，无法准确识别。

李富强等[31]提出虚拟磁通的概念，利用虚拟磁通在励磁涌流情况下不对称，而在内部故障情况下对称来识别变压器的运行状态。赵永斌等[32]利用磁通斜率波形前后半波的对称度来判别，当三相中任一相对称度低于整定系数则判定为区内故障，只有三相对称度均高于整定系数才判定为励磁涌流。赵晓坦等[33]提出采用差动电流一周波内最大、最小值处，对应的磁通轨迹曲线倾角的正弦值之差作为判别励磁涌流和区内故障的判据。

2.7 励磁涌流智能识别算法

2.7.1 人工神经网络识别法

人工神经网络ANN(Artificial Neural Networks)具有自学习、联想存储功能和高速寻找优化解的能力。Perez L G等[34]最早将ANN应用于变压器保护，随后大量科研工作者在此基础上进行了深入的研究。

段玉倩等[35]较早的建立了一个包含输入层、隐含层和输出层的三层前向神经网络，并以变压器两侧的电流量做为神经网络的输入信号，用来实现变压器的微机保护。MingJie Chen等[36]利用ANN来逼近变压器的电磁关系，构建了可以替代变压器物理模型的ANN模型，在线识别变压器的内部参数来判别其运行状态。

ANN有着智能高速寻找优化解处理复杂问题的能力，文献[35]和[36]都表明基于ANN的变压器保护系统能在10ms内响应动作。但其设计过程繁琐，具体步骤如下：①选择合适的ANN类型；②输入层节点数目确定，即有多少特征量需要输入；③经过多次试验后确定隐含层中的节点数；④选择合适的传递函数；⑤取得作为训练样本的原始数据；⑥样本原始数据的筛选及特征量的提取；⑦训练。

上述训练过程需反复进行，一旦不满足设计要求则需调整后重新训练。并且需要大量的输入数据来作为训练样本，而每台变压器的参数及其所处的系统环境不同，实际中难以事先获取大量训练样本，即难以保证训练样本的完备性，潜伏着误判的可能。

2.7.2 小波变换识别法

小波变换具有多尺度分析和良好的时频局部细化特点，因此能能够充分突出信号某些方面的特征。Zhang Chuanli等[37]最早将小波变换用于识别励磁涌流与内部故障电流。

在变压器差动保护中，小波变换主要集中于高次谐波检测[38]和奇异点检测[39]。高次谐波检测中，励磁涌流的高频细节会呈周期性突变，而内部故障电流仅突变一次，之后便会衰减为零。奇异点检测则是将励磁涌流通过小波变换后，所得的波形有周期性奇异点出现，而内部故障电流变换后的波形无奇异点来判别。

在实际应用中，为了准确的获得高频分量以及突变特征量，需要提高采样频率，从而需要使用运算速度更快的微机处理器。随着科学技术的不断进步，如今的ARM和DPS微机处理器已经完全可以满足微机保护系统的设计需求。

然而，电力系统中高频谐波以及周围环境中高频噪声容易对小波变换产生干扰，因此需要进一步研究，以提高小波变换的抗干扰能力。

2.7.3 模糊逻辑多判据识别法[40-42]

变压器励磁涌流具有不确定性与复杂性，却又和故障电流有着诸多共性。每种识别判据都存在着自己的局限性，单一的判据无法准确识别所有情况，因此需要综合利用各判据的优点，而模糊逻辑多判据识别法正是为了实现这一目的而提出的。

黄登峰等[41]将二次谐波制动原理、波形比较原理、功率差动原理和低电压判别法综合模糊化后，用一个总的隶属度来综合上述多判据，如式(7)所示：

μ=ω1μ1+ω2μ2+ω3μ3+ω4μ4

(7)

其中ω1、ω2、ω3、ω4是该判据的权重，并且满足ω1+ω2+ω3+ω4=1。当μ大于整定值时，判定为区内故障，否则判定为励磁涌流。

该方法仍是一个新的探索方向，在设计过程中，如何选择各判据的“隶属函数”和“权重”仍是较难解决的问题。针对这个问题，王增平等[42]建立了基于Choquet积分的k可加模糊测度的计算模型，k可加模糊测度在测度的复杂性和表示能力方面做了折中，通过较小的计算量就能得到能够反映各判据关系的重要性测度。

3 总结与展望

尽管识别变压器励磁涌流与区内故障电流的方法种类繁多，近年来许多科研工作者又相继提出诸多新的判别方法或是在原有方法的基础上加以改进。但由于励磁涌流受多种因数的影响，因而具有不确定性和复杂性。现有的识别方法都还不够完善，因此必须寻求更有效的励磁涌流识别方法。该途径应能尽可能完全的提取和利用变压器发生励磁涌流及内部故障时所存在的差异性，例如深度学习算法。

另外，仅以一种识别方法难以应对实际运行中的所有情况，即存在误动作或拒动作的可能性。而将现有的多种性能较好的识别方法有机的组成一个具有更高性能的变压器差动保护系统，综合利用各种识别方法的优点，弥补各自的缺点，将使变压器差动保护具有更高的正确动作率，因此可以进一步深入研究模糊逻辑算法在变压器保护中的应用。

随着科学技术的不断发展，相信在不久的将来，变压器受励磁涌流困扰的问题将得到彻底解决。

[1] 沈晓凡,舒治淮,吕鹏飞,等.2006年国家电网公司继电保护装置运行情况[J].电网技术,2008,3:18-21.

[2] 马静,王增平.基于标准化网格曲线时频域分析的励磁涌流鉴别新方法[J].电工技术学报,2007,9:159-166.

[3] Lin X N,Liu P,Malik O P.Studies for identification of the inrush based on Improved Correlation Algorithm[J].IEEE Trans on Power Delivery,2002,17(4):901-907.

[4] 焦邵华,刘万顺.区分变压器励磁涌流和内部短路的积分型波形对称原理[J].中国电机工程学报,1999,8:35-38.

[5] 董洁,于莉萍,焦志先,等.变压器差动保护涌流制动原理的研究[J].电力系统自动化,1997,12:30-33.

[6] 和敬涵,李静正,姚斌,等.基于波形正弦度特征的变压器励磁涌流判别算法[J].中国电机工程学报,2007,4:54-59.

[7] Shang G C,Yu D C.Identifying internal faults of transformers through the similarity degree between voltage and current[C].IEEE PES Winter Meeting,2000:1868-1872.

[8] 李贵存,刘万顺,滕林,等.基于波形相关性分析的变压器励磁涌流识别新算法[J].电力系统自动化,2001,17:25-28.

[9] 李贵存,刘万顺,刘建飞,等.用波形拟合法识别变压器励磁涌流和短路电流的新原理[J].电力系统自动化,2001,14:15-18.

[10] 陈德树,尹项根,张哲,等.虚拟三次谐波制动式变压器差动保护[J].中国电机工程学报,2001,8:20-24.

[11] 尤夏,张艳霞.波动误差结合峰-峰间距法识别变压器励磁涌流[J].电力系统自动化,2012,14:36-40+45.

[12] 郝文斌,李群湛,黄咏容,等.基于支持向量机的励磁涌流识别算法[J].西南交通大学学报,2007,4:490-493.

[13] 焦尚彬,黄璜,赵黎明,等.基于双曲S变换的变压器励磁涌流和内部故障识别新方法[J].电力系统保护与控制,2011,16:114-120+138.

[14] 边铁.基于希尔伯特黄变换的变压器励磁涌流识别新原理[D].华北电力大学(河北),2009.

[15] 郑涛,刘万顺,肖仕武,等.一种基于数学形态学提取电流波形特征的变压器保护新原理[J].中国电机工程学报,2004,7:22-28.

[16] Armando Guzman,Stan Zocholl,Gabriel Benmouyal,et al.A Current Based Solution for Transformer Differential Protection-Part I:Problem Statement[J].IEEE Transaction On Power Delivery,2001,16(10):485-491.

[17] Armando Guzman,Stan Zocholl,Hector J Altuve.A Current Based Solution for Transformer Differential Protection-Part II:Relay description and evaluation[J].IEEE Transaction On Power Delivery,2002,17(4):886-893.

[18] 王立大,段周朝.变压器励磁涌流引起保护误动分析[J].电力系统保护与控制,2010,10:138-140+144.

[19] 骆健,吴罡明,丁大德.一种高可靠的自适应励磁涌流制动方法[J].电力系统自动化,2010,2:80-83.

[20] 袁宇波,陆于平,李澄,等.三相涌流波形特征分析及差动保护中采用二次谐波相位制动的原理[J].中国电机工程学报,2006,19:23-28.

[21] 王祖光.间断角原理变压器差动保护[J].电力系统自动化,1979,1:18-30.

[22] 李宏任.实用继电保护[M].北京:机械工业出版社,2002.

[23] 黄登峰,郁惟镛,赵亮,等.基于模糊多判据的变压器励磁涌流识别新算法[J].继电器,2000,12:4-7+12.

[24] Thorp J S,Phadkel A G.A microprocessor based voltage restraint there phase transformer differential relay[J].Proceeding of the south eastern symposium on system theory,1982,4:312-316.

[25] 马静,王增平,吴劼.基于广义瞬时功率的新型变压器保护原理[J].中国电机工程学报,2008,13:78-83.

[26] 古斌,谭建成.基于有功无功直流分量比值的变压器涌流新判据[J].电力系统自动化,2007,20:65-69.

[27] 郝治国,张保会,褚云龙,等.基于等值回路平衡方程的变压器保护原理[J].中国电机工程学报,2006,10:67-72.

[28] 马静,王增平,王雪.基于等效瞬时漏电感的变压器保护新原理[J].电力系统自动化,2006,23:64-68+103.

[29] Keizo Inagaki,Masaru Higaki,Yoshiaki Matsui,et al.Digital Protection Method for Power Transformers Based on an Equivalent Circuit Composed of Inverse Inductance.IEEE Trans on Power Delivery,1988,3(4):1501-1510.

[30] Phadke A G,Thorp J S.A New Computer Based Flux Restrained Current Differential Relay for Power Transformer Protection.IEEE Trans on Power Apparatus and Systems,1983,102(11):3624-3629.

[31] 李富强,刘秀成,李东霞,等.基于虚拟磁通与差动电流特性识别变压器励磁涌流[J].电力系统自动化,2004,23:45-49.

[32] 赵永彬,陆于平.基于磁通对称特性的变压器励磁涌流判别新算法[J].电工技术学报,2007,12:66-71.

[33] 赵晓坦,柴建云,苏鹏声,等.利用磁通轨迹特征识别变压器励磁涌流[J].继电器,2004,2:1-5.

[34] Perez L G,Flechsig A J,Meador J L,et al.Training an Artificial Neural Network to Discriminate Between Magnetizing Inrush and Internal Faults[J].IEEE Trans on Power Delivery,1994,9(1):434～441.

[35] 段玉倩,贺家李,贺继红.基于人工神经网络方法的微机变压器保护[J].中国电机工程学报,1998,03:190-194.

[36] MingJie Chen,Xin Zeng,Gonghua Li,et al.A new transformer protection based on the artificial neural network model[C].IEEE Automation Congress(WAC),2008:1- 4.

[37] Zhang Chuanli,Huang Yizhuang,Ma Xiaoxu,et al.A new approach to detect transformer inrush current by applying wavelet transform[J].Power System Technology,1998,2:1040-1044.

[38] Yang Long,Ning Jingdong.A Wavelet Transform Based Discrimination Between Internal Faults and Inrush Currents in Power Transformers[J].IEEE Electric Information and Control Engineering(ICEICE),2011,10:1127- 1129.

[39] 蔡义明,李泽,王巨丰,等.小波分析在变压器励磁涌流识别中的研究[J].广西大学学报(自然科学版),2012,02:371-375.

[40] Ramesh K,Sushama M.Power transformer protection using fuzzy logic based-relaying[C].IEEE Advances in Electrical Engineering(ICAEE),2014:1-7.

[41] 黄登峰,郁惟镛,赵亮,等.基于模糊多判据的变压器励磁涌流识别新算法[J].继电器,2000,12:4-7+12.

[42] 王增平,王雪.基于k可加模糊测度的变压器励磁涌流识别方法[J].电力系统保护与控制,2011,21:45-48+54.

Review of the Methods to Identify Transformer Inrush Current

ZHANGXiao-fan，LANSheng

(College of Electrical Engineering and Automation,Fuzhou University,Fuzhou 350108,China)

The correct action rate of transformer differential protection has been affected by the inrush current,in recent years a large number of domestic and foreign relay protection workers conducted in-depth research,put forward many new excitation inrush current identification methods.In this paper,the methods of domestic and foreign each proposed to identify inrush current and internal fault current were collected,analyzed and summed up the advantages and disadvantages.Finally,future research direction to solve the inrush current problem were proposed.

transformer;magnetizing inrush current;differential protection

1004-289X(2016)03-0001-06

TM41;TM771

B

2015-03-27

张小钒(1989-)，男，硕士研究生，研究方向为电力系统继电保护； 兰生(1971-)，男，博士，副教授，研究方向为等离子体、特高压输电和电磁生物效应。