新型MMC-HVDC控制策略的研究*

陈 莉， 陈 乾， 陈 剑， 代高富

南京铁道职业技术学院 南京 210031

新型MMC-HVDC控制策略的研究*

陈 莉， 陈 乾， 陈 剑， 代高富

南京铁道职业技术学院 南京 210031

MMC-HVDC系统的核心功能是对有功功率和无功功率进行控制，从而实现换流站直接功率的输送。从MMC-HVDC的系统结构出发，推导了其数学模型，设计了dq坐标系下的有功和无功解耦控制器，实现了有功和无功的解耦控制，并在PSCAD环境下进行了仿真验证。

模块化多电平换流器； 高压直流输电； 解耦控制

1 MMC-HVDC系统结构

图1所示为双端MMC-HVDC(模块化多电平换流器-高压直流输电)系统单线图，图2所示为系统主电路拓扑图。两个交流系统的电能输送依靠两个背靠背的MMC换流站和中间的直流线路完成，每个MMC换流站的各相桥臂由若干个子模块级联构成，子模块的数量越多，能够承受的输电电

压等级就越高。这种新型拓扑在高压直流输电领域得到广泛的应用[1-5]。

图1 双端MMC-HVDC系统单线图

图2 MMC-HVDC系统主电路拓扑图

2 MMC-HVDC数学模型

由于MMC-HVDC系统的整流侧和逆变侧结构相同，以整流侧为例推导其数学模型。图3是忽略桥臂损耗情况下整流侧MMC等效电路图。

根据图3列出基尔霍夫方程，得到三相静止坐标系下的MMC数学模型：

(1)

式中：L=Ls+Lm/2。

图3 MMC-HVDC整流侧等效电路图

在三相静止坐标系下，各个电气量均为交流量，不利于得到有功分量和无功分量。为此，需要将上述模型转换到dq坐标系下，得到相应的直流量，这样利于解耦控制器的设计。三相abc坐标系到两相dq坐标系的变换矩阵为：

(2)

对式(1)进行式(2)所示的坐标变换，可以得到dq坐标系下的MMC数学模型：

(3)

根据瞬时功率理论，abc静止坐标系下换流站与交流系统的有功功率和无功功率为：

(4)

转换到dq同步坐标系下，有功功率和无功功率可表示为:

(5)

选择d轴与电网电压旋转向量重合，即usq=0，可以简化计算，将式(5)改写为：

(6)

3 dq坐标系下解耦控制器的设计

dq坐标系下的解耦控制器是电压源换流器领域的一种经典控制方法，其系统结构如图4所示。这种控制器由外环控制器和内环电流控制器构成，外环控制器用于实现有功和无功分量的控制，输出量是内环电流控制器需要的参考电流值。内环电流控制器则是跟踪电流参考值，输出换流器需要的输出电压参考值，即调制波，最后通过均压调制得到PWM(脉冲宽度调制)触发脉冲。

图4 一端换流站直接电流控制原理图

3.1 外环控制器的设计

MMC-HVDC系统中外环控制器的作用是根据有功功率、无功功率及直流电压参考值计算出内环电流控制器需要的电流参考值idref、iqref。外环控制器主要分为定有功控制、定无功控制和定直流电压控制[6-7]。

定有功控制的原理是将给定的有功功率参考值Pref与实际测得的有功功率P比较，经过PI(比例积分)控制器形成闭环控制，实现对交流系统和换流站之间的有功输送，控制器的输出是内环控制器d轴参考电流idref。定无功控制的原理与定有功控制相似，将系统无功功率的测量值Q与给定的无功功率参考值Qref比较，经过PI控制器实现无功功率的调节，控制器的输出是内环控制器q轴参考电流iqref。为了稳定直流母线电压，需要定直流电压控制器[8]，其原理是将给定的直流母线电压参考值udcref和实际测量得到的直流电压值比较，通过PI控制器来调节直流母线电压，从而实现电压稳定[9-10]，控制器的输出是内环控制器d轴参考电流idref。三种控制器的控制框图如图5所示。

图5 外环控制器控制框图

3.2 内环控制器的设计

由式3所示dq坐标系下的数学模型可以看出，由于耦合电感的存在，d、q轴电压含有电流交叉耦合量ωLiq、ωLid，这不利于对有功功率和无功功率进行独立控制。为了消除d、q轴之间的耦合，可以将式(3)改写为：

(7)

式中：Rid+Ldid/dt、Riq+Ldiq/dt分别与id、iq构成一阶微分关系，可通过PI控制器来实现。引入电压耦合补偿项ωLid、ωLiq及电压前馈分量usd、usq，可以得到换流器在d、q轴的参考电压信号：

(8)

根据式(8)，得到如图6所示的MMC内环电流控制结构图。

图6 MMC内环控制结构图

4 仿真分析

为验证上述dq坐标系下解耦控制策略的正确性，在PSCAD/EMTDC中搭建了双端MMC-HVDC系统仿真模型，其主电路结构如图7所示。换流站MMC1端为整流侧，采用定有功和定无功控制方式，换流站MMC2端为逆变侧，采用定直流电压和定无功控制方式。

图7 连接有源网络的MMC-HVDC仿真模型

主电路结构模型的仿真参数见表1。

表1 仿真参数

项目设定值桥臂子模块数20桥臂电感/mH10子模块电容/μF4000网侧线电压有效值/kV35直流侧电压/kV60开关频率/Hz2000交流电压频率/Hz50系统容量/MVA60直流电缆长度/km10

4.1 功率阶跃响应

为验证MMC-HVDC系统的功率阶跃响应特性，仿真设置t=0.5s时，MMC1端向MMC2端输送有功功率参考值从0.8pu阶跃到0.4pu；在t=0.8s 时，MMC1端向MMC2端输送无功率参考值从0阶跃到0.3pu。所得到的仿真波形如图8所示。

由图8可以看出，控制系统对有功功率和无功功率的跟踪效果较好，在t=0.5s时，MMC1换流站向MMC2换流站输送的有功功率从0.8pu阶跃到0.4pu，有功功率经过0.1s的短暂调整跟踪到新的指令值，并且MMC2换流站的有功功率也从-0.8pu 阶跃到-0.4pu。在t=0.8s时，MMC1换流站向MMC2换流站输送的无功功率从0阶跃到0.3pu，无功功率得到了很好的跟踪控制。并且，在有功功率阶跃时，无功功率有少许波动；在无功功率阶跃时，有功功率也出现了一些波动；两种情况下的波动都没有超过10%。总体而言，dq坐标系下的解耦控制可以实现有功和无功的独立控制。

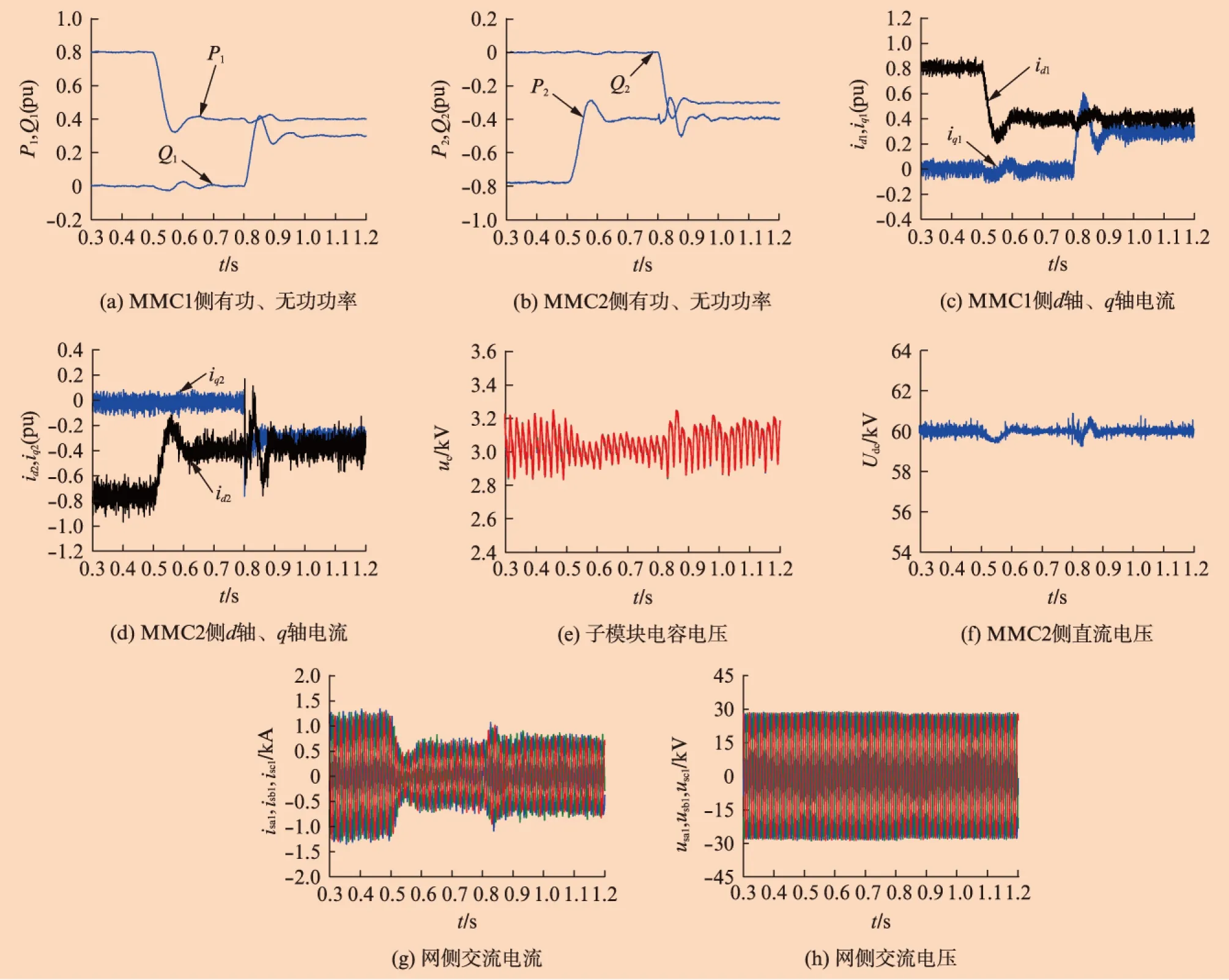
图8 功率阶跃响应仿真结果

由图8还可以看出，在功率阶跃变化时，子模块电容电压出现波动，这是由于功率变化时，电容电压会进行充放电，引起了电容电压的波动。MMC2侧采用定直流电压控制方式，直流母线电压维持在60kV，在功率阶跃时有一些波动，但波动范围没有超出±1kV，并且很快恢复稳定。此外，当功率阶跃变化时，网侧电流会发生相应的改变，而电流电压基本不变，这是因为功率的输送是通过电流的改变完成的，电压则保持恒定。

4.2 潮流翻转响应

MMC-HVDC系统能量可以双向流动，为验证潮流翻转响应特性，仿真设置在t=0.5s 之前，MMC1换流站向MMC2换流站输送有功功率0.4pu、无功功率0.2pu；在t=0.5s时，有功功率开始反送，MMC2换流站向MMC1换流站输送有功功率0.4pu；在t=0.8s时，无功功率开始翻转，MMC2换流站向MMC1换流站输送无功功率0.3pu。图9给出了潮流翻转的仿真结果。

由图9可以看出，有功功率和无功功率在翻转时，MMC1换流站经过短暂的调整时间跟踪到了指令值，并很快恢复稳定，系统超调量较小，响应速度较快，实现了有功和无功的解耦控制。MMC2换流站在无功功率发生翻转时，有功功率波动比较大，经过0.3s的轻微震荡恢复稳定，这是由于MMC2侧采用定直流电压控制、潮流翻转电容充放电造成的，最终系统还是实现了有功和无功的解耦控制。

由图9还可以看出，在潮流翻转时，MMC1换流站A相上桥臂子模块电容电压也会进行充放电，电压从而发生波动，但经过短暂的调整时间恢复了稳定，波动范围在10%以内。此外，潮流翻转时，电压极性没有发生改变，且直流电压的波动也很小，波动范围没有超出±2kV。

4.3 直流电压阶跃响应

MMC1换流站向MMC2换流站输送的有功功率为0.8pu，无功功率为0，为了验证直流电压发生阶跃变化时MMC-HVDC系统的响应特性，在t=0.5s时，直流电压从60kV阶跃到65kV，图10给出了系统的仿真结果。

图9 潮流翻转响应仿真结果

图10 直流电压阶跃响应仿真结果

由图10可以看出，直流母线电压从60kV提高到65kV时，MMC1换流站的有功功率、无功功率、d轴电流和q轴电流基本不受影响，仅出现了微小的波动，MMC2换流站的无功功率、q轴电流在直流电压变化时也基本不受影响。由于MMC2换流站采用定直流电压和定无功控制方式，有功功率和d轴电流出现了小幅波动，但迅速回到了目标值。在t=0.5s 直流电压提高时，MMC1换流站A相上桥臂子模块电容也开始充电，即相应增大，但并没有影响子模块电容电压的均衡。所以，直流电压的阶跃变化不会影响两个换流站有功功率和无功功率的输送。

5 结论

笔者根据MMC-HVDC系统的结构，建立了三相静止坐标系和dq坐标系下的数学模型，并设计了基于dq坐标系的解耦控制策略，最后在PSCAD/EMTDC平台搭建了仿真模型，分析了功率阶跃、潮流翻转及直流电压阶跃三种工况下的响应特性。

(1)dq坐标系下的解耦控制器可以实现有功功率和无功功率的独立调节，具有良好的解耦特性。

(2) 在功率变化时，系统响应速度较快，可以很快跟踪到指令值，具有较好的稳态和动态特性。

(3) 两个换流站之间的能量可以双向流动，直流电压的极性不发生改变。

(4) 直流电压的变化并不影响有功功率和无功功率的输送。

[1] 韦延方,卫志农,孙国强,等.一种新型的高压直流输电技术——MMC-HVDC[J].电力自动化设备,2012,32(7)： 1-9.

[2] 孔明,汤广福,贺之渊,等.不对称交流电网下MMC-HVDC输电系统的控制策略[J].中国电机工程学报,2013,33(28)： 41-49.

[3] 张建坡.赵成勇,孙海峰.基于改进拓扑的MMC-HVDC控制策略仿真[J].中国电机工程学报,2015,35(5)： 1032-1040.

[4] 管敏渊,徐政.MMC型VSC-HVDC系统电容电压的优化平衡控制[J].中国电机工程学报,2011,31(12)： 9-14.

[5] 张碧涵,赵海森.基于PSCAD仿真的柔性直流输电技术研究[J].上海电气技术,2016,9(2)： 56-63.

[6] 潘伟勇.模块化多电平直流输电系统控制和保护策略研究[D].杭州： 浙江大学,2012.

[7] 胡敬伟.模块化多电平换流器型高压直流输电的启动控制策略研究[D].长沙： 湖南大学,2014.

[8] 管敏渊.基于模块化多电平换流器的直流输电系统控制策略研究[D].杭州： 浙江大学, 2013.

[9] 周杨.基于模块化多电平换流技术的柔性直流输电系统研究[D].杭州： 浙江大学,2013.

[10] 徐政，屠卿瑞，管敏渊，等.柔性直流输电系统[M].北京： 机械工程出版社, 2013.

Core function of MMC-HVDC system focuses on the control of active power and reactive power in order to realize the direct power transmission at converter station. The MMC-HVDC mathematical model was derived from the structure of MMC-HVDC system while the decoupling controllers for active and reactive power were designed in thedqcoordinate system and a simulation demonstration was carried out under PSCAD environment.

MMC； HVDC； Decoupling Control

*江苏省高职院校青年教师企业实践培训项目(编号： 2016QYSJ036)

2016年7月

陈莉(1985— )，女，硕士，助教，主要研究方向为铁道供电技术。 E-mail： 552008231@qq.com

TM72

A

1674-540X(2016)03-015-06