地质统计学在桂中三水铝矿床勘查评价中的应用

黄国有,卢光辉,林最近,苟晓利

(广西壮族自治区二七四地质队,广西北海 536005)



地质统计学在桂中三水铝矿床勘查评价中的应用

黄国有,卢光辉,林最近,苟晓利

(广西壮族自治区二七四地质队,广西北海 536005)

桂中三水铝矿床是我国唯一的大型三水铝矿床，初步查明(333+334)铝土矿资源量7.7亿吨。本文介绍地质统计学方法在桂中三水铝土矿床勘查和资源量评价中的应用，包括桂中三水铝矿床典型矿区变异函数的计算和模型拟合；最优变异函数模型的确定；利用变异函数变程确定最佳勘查工程间距的实例分析；利用地质统计学方法进行矿体边界和资源量类别的自动化划分以及资源量估算。

三水铝 地质统计学 变异函数 勘查评价 资源量估算

0 前言

地质统计学是地质大数据处理的一个统计学分支，它以区域化变量理论为基础，以变异函数为工具，研究空间分布上既有随机性、又具有结构性的含矿率和品位等变量的变化规律，以此指导矿产勘查和资源评价工作。侯景儒等(2001)利用地质统计学分析了资产资源分类估算问题，徐俊龙等(2014)利用地质统计学对勘查数据进行结构分析，说明地质统计学方法在地质勘查评价中得到了越来越广泛的应用。广西桂中地区三水铝矿资源丰富，但地质工作程度较低，前人的研究主要集中在矿床特征和成因方面(邓军，2006；卢元庆等，2007；王瑞湖等，2011)，勘查和资源评价方法的研究较少。桂中三水铝矿床规模大、地质变化复杂、数据处理量大，采用地质统计学进行勘查和资源评价可以极大地提高效率和精确度。笔者在参与广西地矿局与中国地质大学合作的“桂中三水铝矿勘查研究”项目的基础上，对该区勘查数据进行地质统计学分析，研究勘查间距的确定、矿体边界的自动划分、资源量的自动化分类和估算的新技术方法。

1 矿床地质概况

广西桂中地区高铁三水铝矿床是我国唯一的大型三水铝矿床，分布于贵港、南宁、来宾等地(图1)，区域构造上处于西大明山-大瑶山隆起和桂中凹陷的接合部位。矿床分布区地层从古生代至第四系均有出露，中泥盆统至下三叠统以碳酸盐岩为主，其余地层以碎屑岩为主。主要褶皱有宾阳-黎塘复式向斜、镇龙山穹隆、大明山背斜和都安-马山倒转褶皱系；主要断裂有NE向的下雷-灵马断裂、凭祥-东门断裂和凭祥-大黎断裂带以及NW向的南丹-昆仑关断裂和右江断裂带。主要岩浆岩有大明山西坡奥陶纪基性火山岩、大明山中部志留纪中细粒二长花岗岩、府城-陈村岭晚白垩世中性火山岩、宾阳昆仑关燕山期斑状二长花岗岩、贵港龙头山燕山期花岗闪长岩和桂平西山燕山期花岗斑岩等。区内断裂和褶皱等地质作用使铁铝岩系抬升、破碎、风化、淋滤、堆积形成三水铝土矿床。

桂中三水铝土矿赋存于第四系更新统钙红土风化壳的中上部，分布于岩溶准平原或宽缓的低丘、矮岭或台地上，具有明显的垂直分带现象：上部为红土带，中部为铝土矿带，下部为杂色粘土带，基底为泥盆系-石炭系碳酸盐岩。矿层呈层状展布，产状与自然地形一致。矿石呈胶结团块状，具豆粒结构、鲕粒结构或铁壳结构。平均含矿率589kg/m3，Al2O3平均品位24.95%。经预-普查探获(本次研究估算的)资源量7.7亿吨。

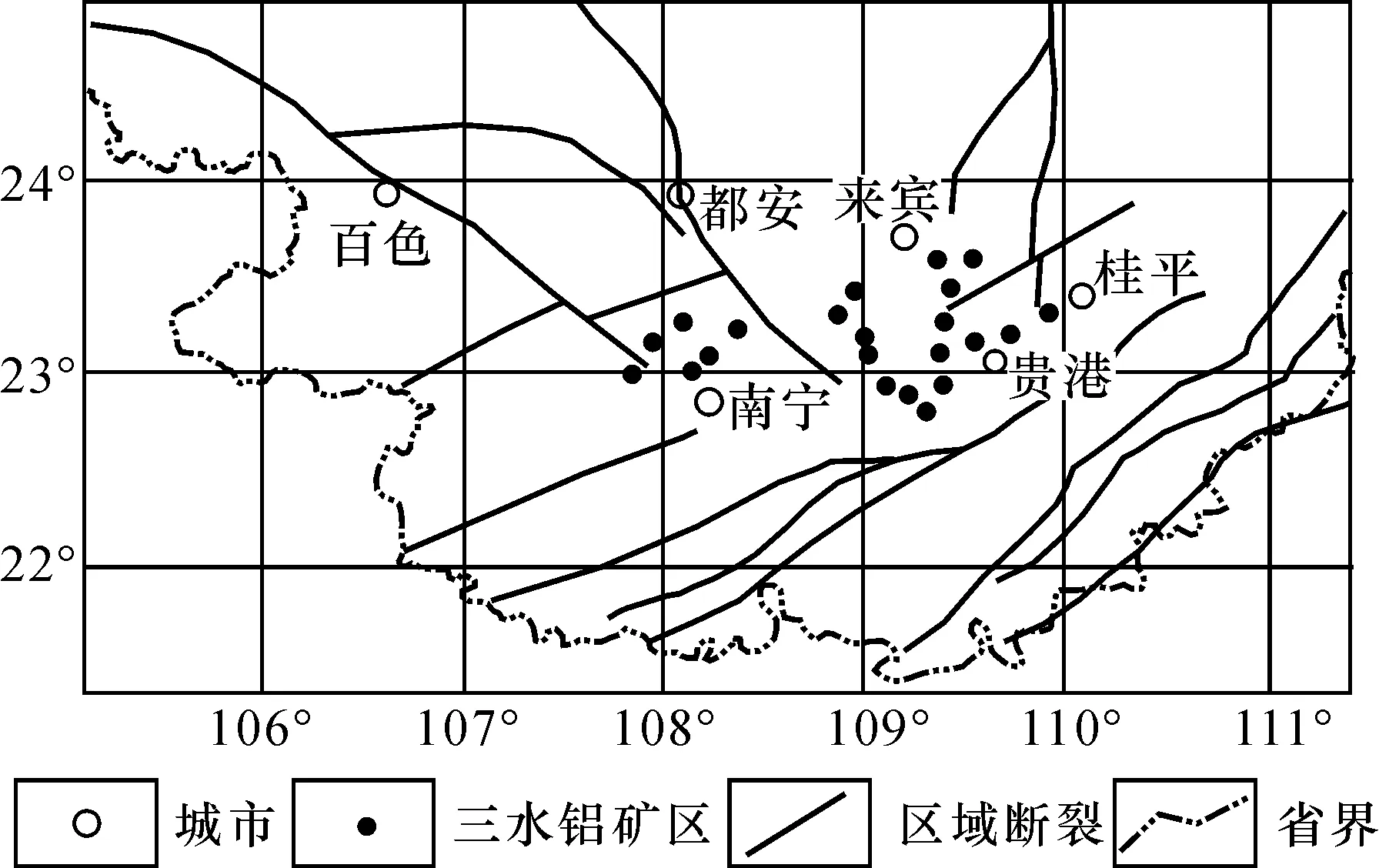
图1 桂中三水铝矿构造位置图

2 矿床变异函数模型的拟合方法

矿层厚度、含矿率和品位等区域化变量Z(x)是一个随机函数，具有局部性、随机性、连续性、变化性和相关性的特点。变量在点x处的随机变量Z(x)与偏离空间距离为h(滞后距、步长)的点(x+h)处的随机变量Z(x+h)之间具有某种程度的自相关性，这种结构的自相关性可用变异函数来描述。变异函数依赖于两个自变量x和h，但在二维平稳假设条件下，在具体矿床或矿体范围，变异函数往往仅依赖于距离h而与位置x无关，这时，变异函数γ(h)的实验值可以用样品分析数据由下式计算(Blaisetal.，1968；Sarma，2002)：

这是众所周知的半方差计算公式(N是参加统计的间距为h的样品对的个数)。变异函数和半方差是同一概念的“理论”和“实践”两个方面，变异函数代表的是一种数学模型，半方差代表的则是该模型的一种实测值。实测值包括了复杂的随机性和误差等因素，理论模型则是理想的数学模型。

变异函数的理论模型有：球状模型、指数模型和高斯模型(何绍渊，1975；陈建宏等，1994)。

球状模型公式为：

a为变程，h为滞后距(步长)，C0为块金常数，表示近距离的变异程度，C为局部先验方差，C0+C为基台值。

指数模型公式为:

该模型的变程为3a。

高斯模型公式为:

对于具体的矿床或矿体而言，其变异函数采用哪种模型，要根据其实测值曲线与模型曲线的拟合程度来确定。下面介绍利用勘查数据计算和拟合变异函数模型的方法步骤。

变异函数的计算方法步骤：(1)找出“足够多”的不同滞后距品位的“数据对”；(2)采用 “数据对”计算品位的半方差，即变异函数的实测值；(3)用半方差实测值展布到图上，制作变异函数的实测值趋势图或曲线图。

变异函数的拟合方法步骤：(1)将变异函数实测值展布到图上，用变异函数的理论模型曲线与实测值曲线进行拟合对比，确定符合该矿床的变异函数模型；(2)用不同滞后距(数据对的间距，即步长)实测值曲线与理论模型曲线进行拟合对比，实测值曲线与理论模型曲线拟合度最佳的步长即为最佳步长，以此确定最优模型。

以贵港大圩矿区Al2O3品位变异函数的计算和拟合为例，为了获得该矿区Al2O3品位的最优变异函数模型，以50m、100m、150m、200m滞后距计算和拟合矿区全向变异函数，结果如图2、图3、图4、图5。图中品位变异函数实测值变化符合球状模型；滞后距取150m时，变异函数的实测值与理论模型曲线的吻合度最高。因而确定滞后距150m的变异函数模型为该区的最优模型(图4)，该模型变程a=800m,C0=3.0,C=2.8。

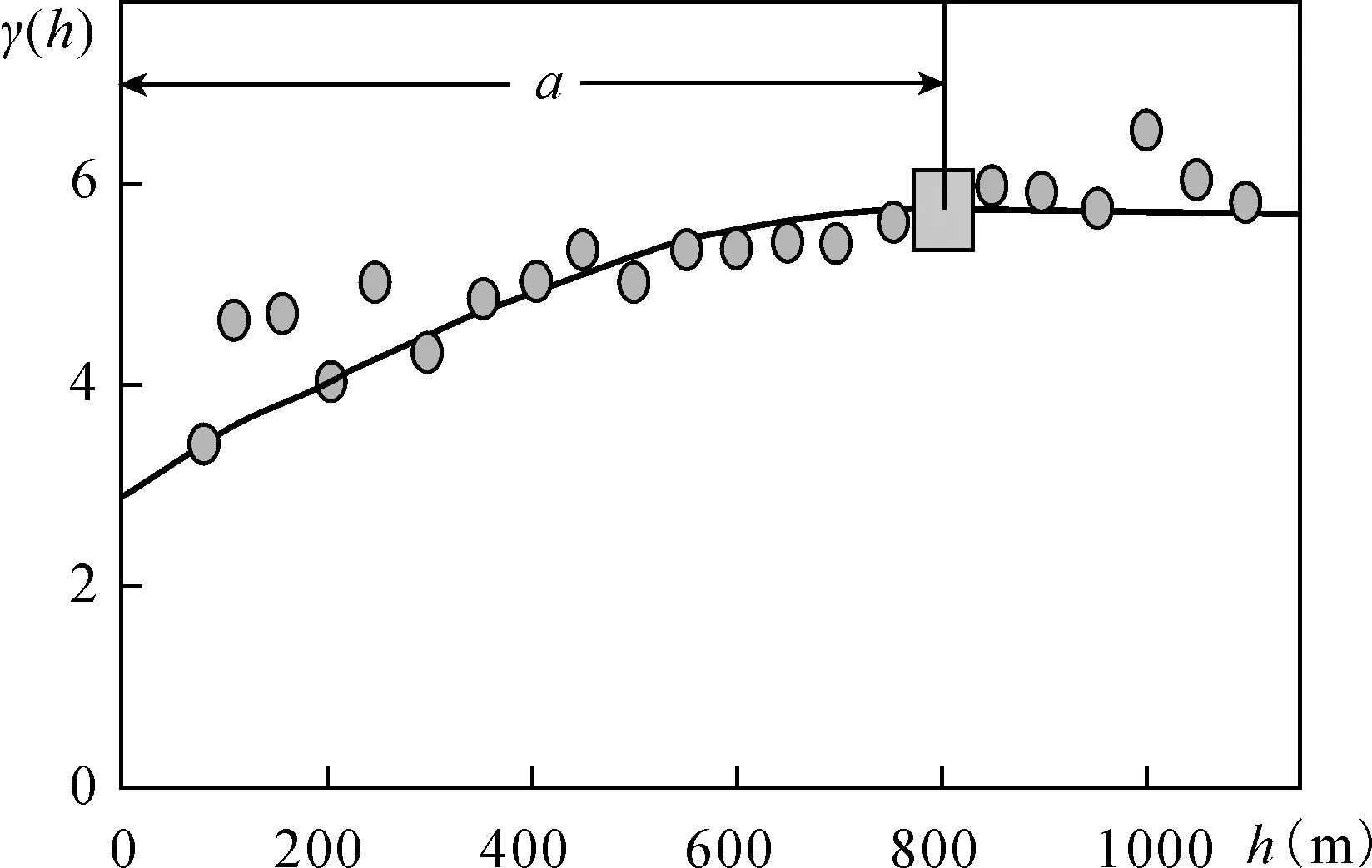
图2 50m滞后距Al2O3品位变异函数

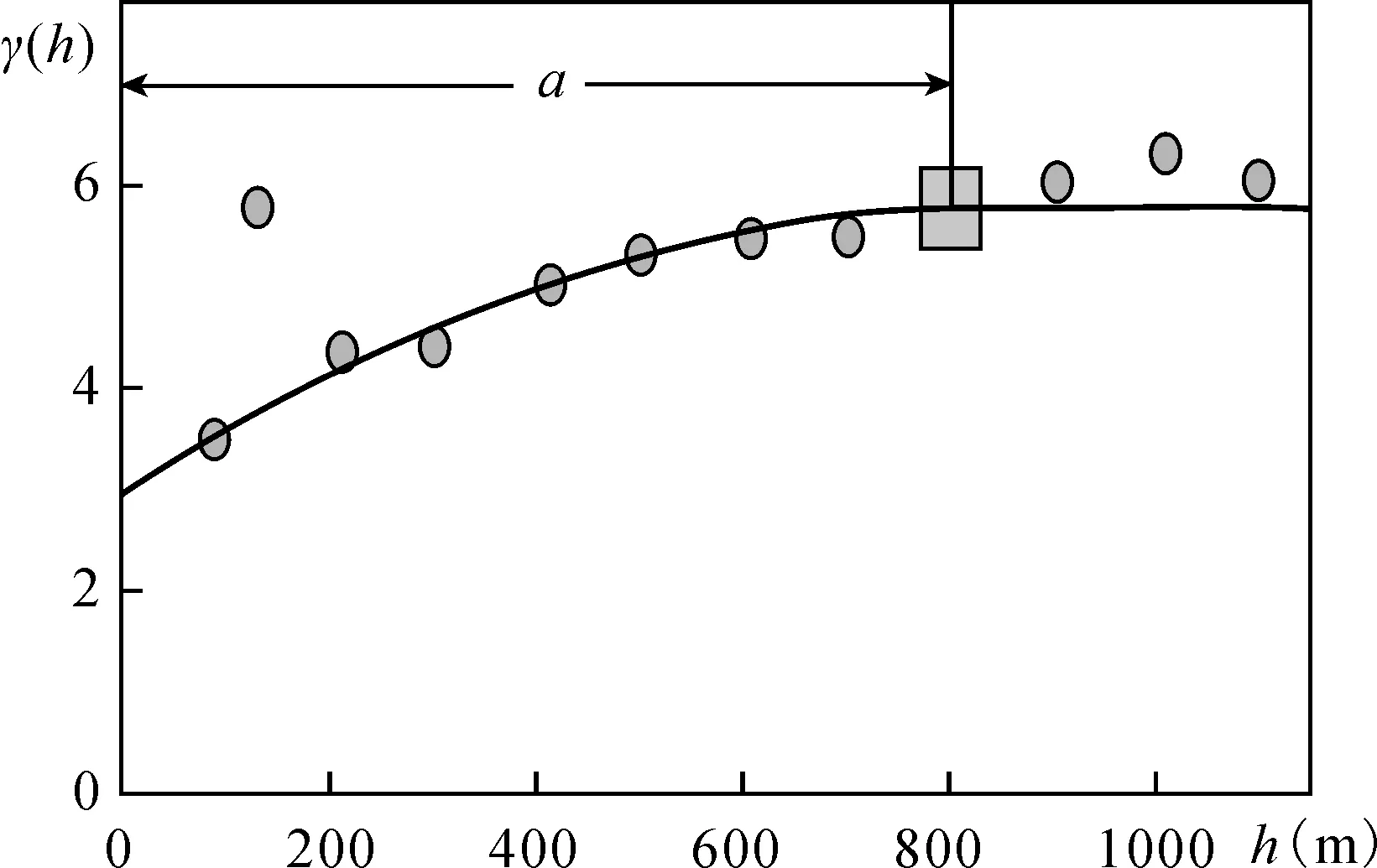
图3 100m滞后距Al2O3品位变异函数

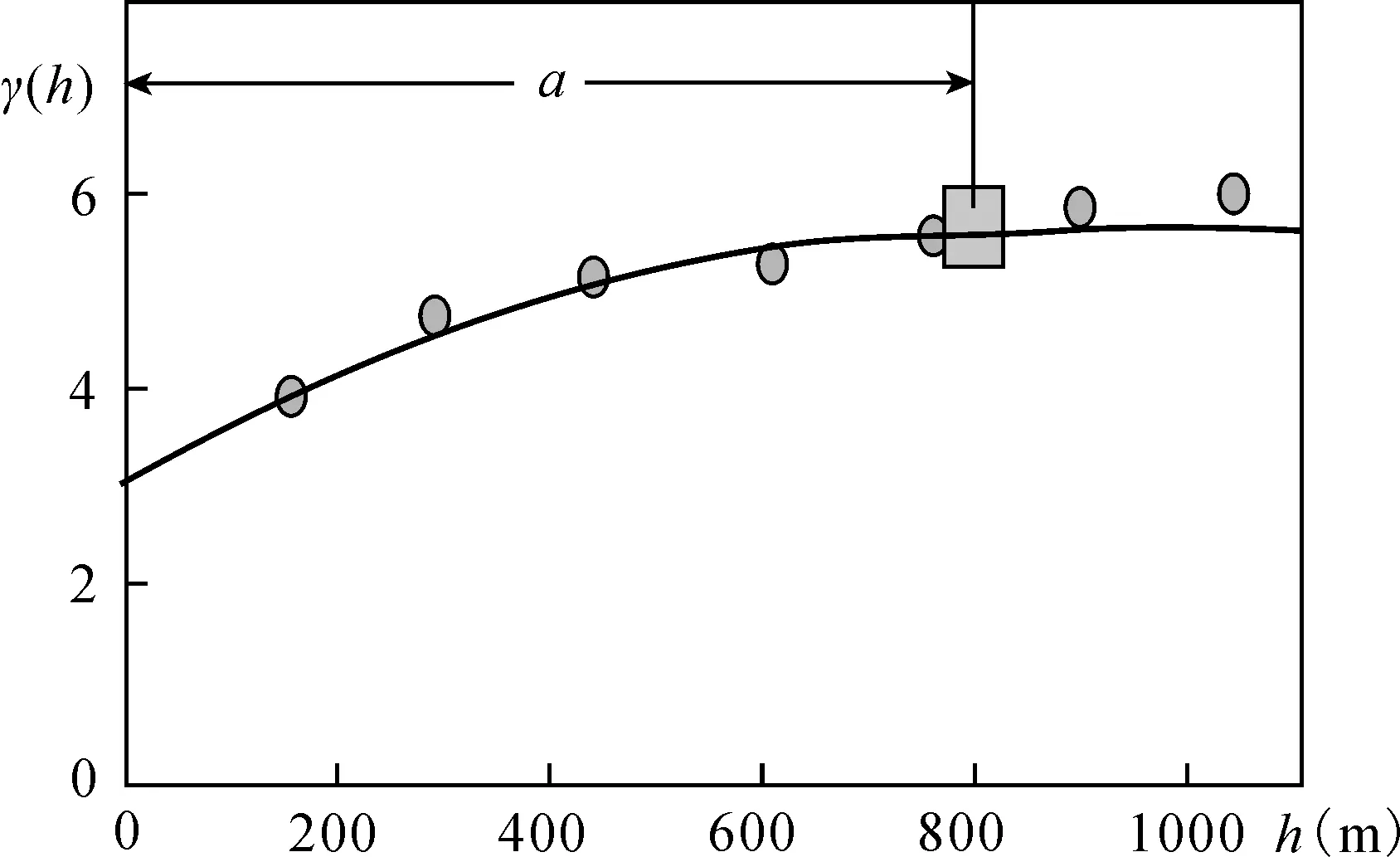
图4 150滞后距Al2O3品位变异函数

图5 200m滞后距Al2O3品位变异函数

3 勘查工程间距的确定方法

变异函数给出了表示近距离变异程度的块金值C0、先验方差C和变程a等丰富的地质规律信息，它是评价工程间距合理性、进行资源储量分类和估算的重要依据(Blaisetal.，1975)。桂中三水铝土矿床属于表生层状矿床，矿层随地形自然起伏分布，含矿率和品位等变量具有较明显的地质统计学规律特征。实际统计表明，各矿区水平方向上的变异函数没有明显的方向性差异；垂直方向即井向变异函数与水平方向的变异函数的块金常数C0和先验方差C也基本相同，不存在明显的带状异向性。对该类型(层状风化壳型)矿床的勘查评价，只需用全向变异函数。

含矿率和Al2O3品位是桂中三水铝土矿资源评价的两个重要指标，统计分析表明，桂中三水铝矿床含矿率和Al2O3品位呈正态分布，典型的马岭矿区样品含矿率和Al2O3品位统计直方图分别如图6和图7。

图6 马岭矿区含矿率直方图

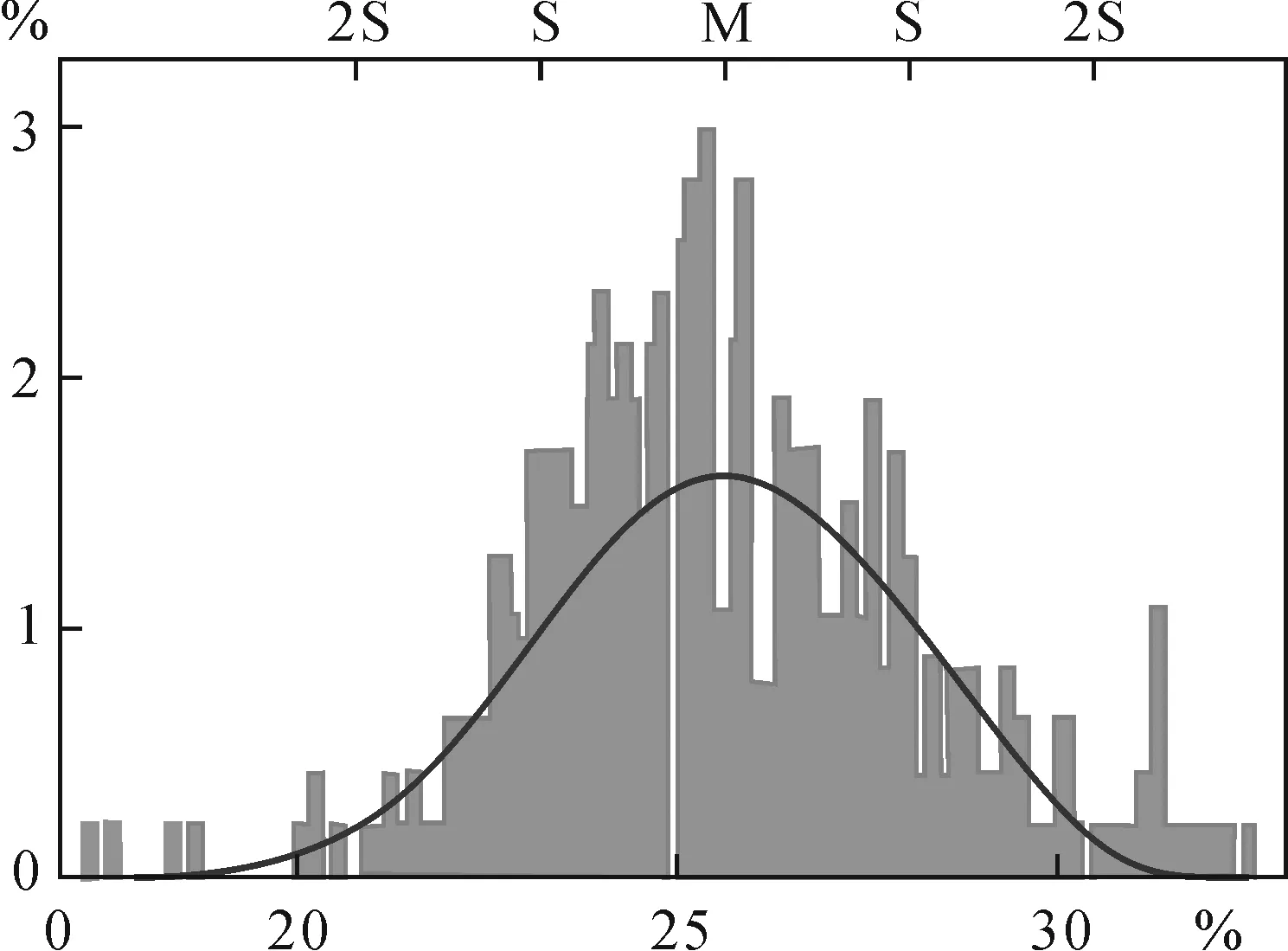
图7 马岭矿区Al2O3品位直方图

下面以横县马岭、贵港邓保和大桥三个典型矿区含矿率和Al2O3品位变异函数为例，研究地质统计学在桂中三水铝矿勘查和资源评价中的应用。所有矿区变异函数的计算和拟合均基于该矿区全部工程样本数据。研究矿层垂直方向(井向)的变异函数时，采用包括非矿样品的全部样品数据；研究矿层平面延伸方向(水平方向)的变异函数时，采用达到边界品位的样品数据。

3.1 横县马岭矿区

横县马岭矿区工程样本分布见图8，利用前述方法计算和拟合得到的含矿率和Al2O3变异函数分别见图9和图10。含矿率和Al2O3变异函数的变程均为200m，表明在已知工程200m范围内，含矿率和Al2O3品位是规律可知的，超出200m范围外则为不可知。因此，探求推断的资源量333的最大工程间距为200m；探求控制的资源量332工程间距为100m；探求探明的资源量331工程间距为50m。

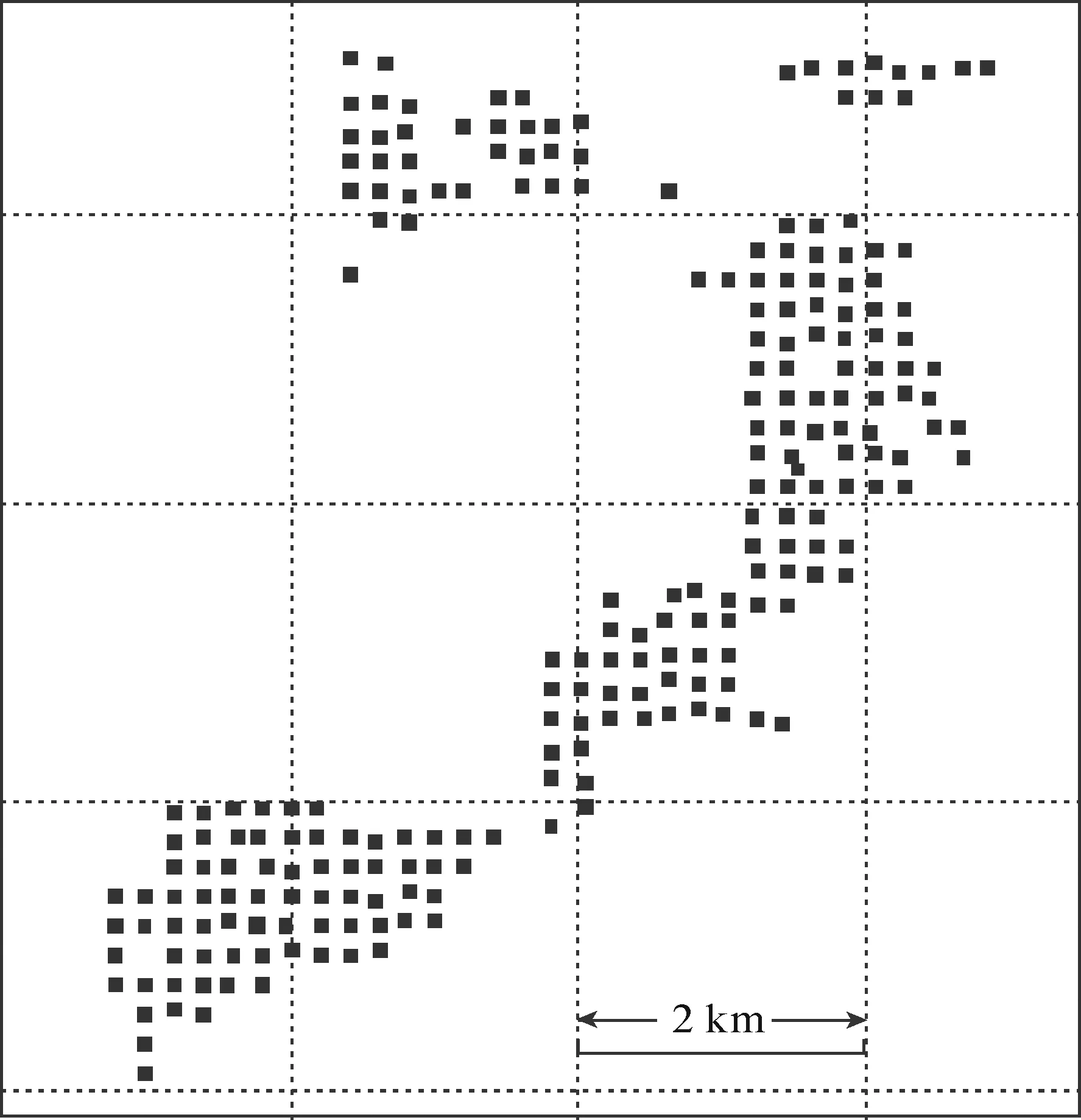
图8 马岭矿区工程样本分布

图9 马岭矿区Al2O3品位变异函数

3.2 贵港邓保矿区

贵港邓保矿区工程样本分布参见图11，利用前述方法计算和拟合得到的含矿率和Al2O3变异函数分别见图12和图13。含矿率和Al2O3变异函数的变程均为400m，在已知工程400m范围内，含矿率和Al2O3品位是规律可知的，超出400m范围外则为不可知。因此，探求333资源量的最大工程间距为400m；探求332资源量工程间距为200m；探求331资源量工程间距为100m。

图10 马岭矿区含矿率变异函数

图11 邓保矿区工程样本分布

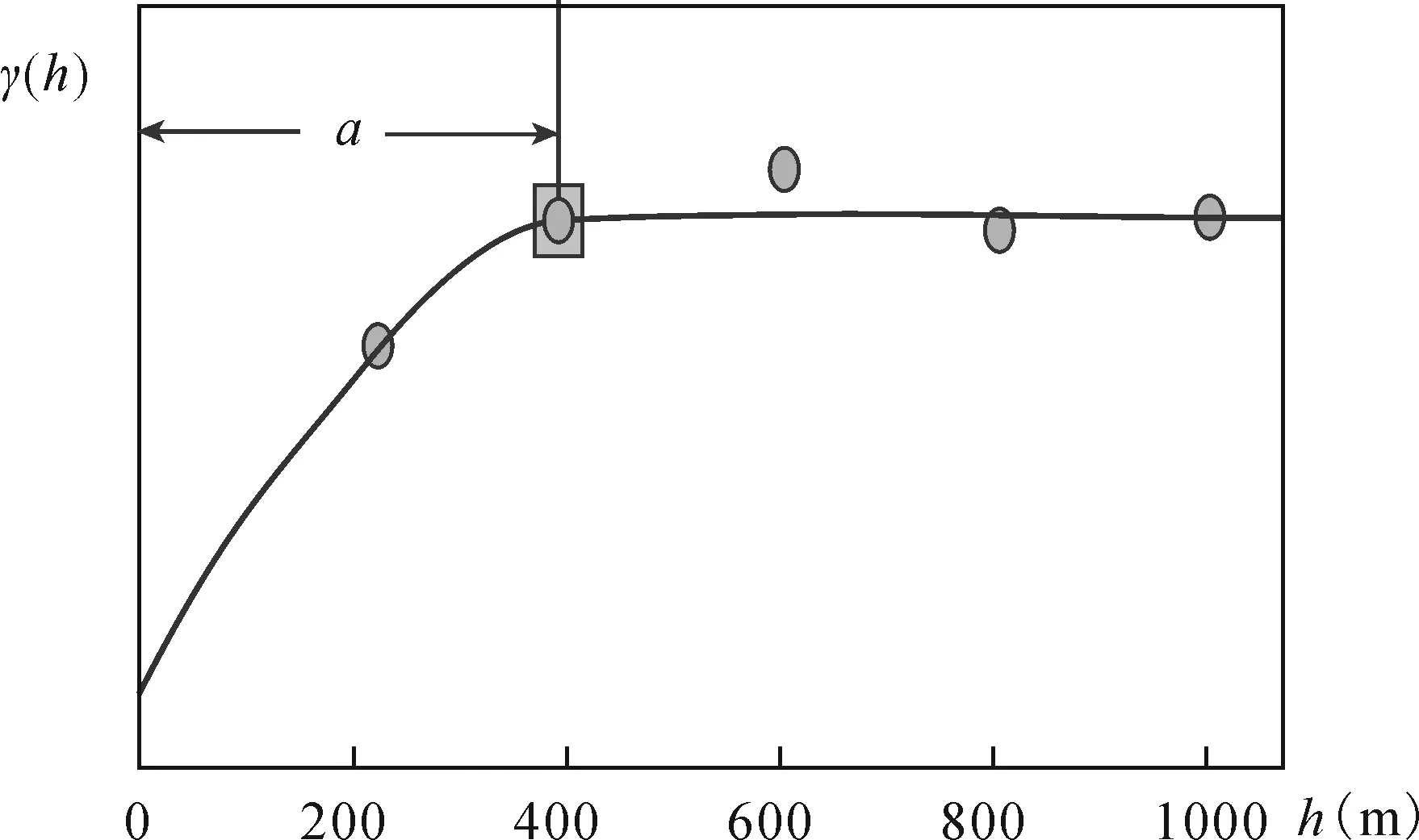
图12 邓保矿区Al2O3品位变异函数

图13 邓保矿区含矿率变异函数

3.3 贵港大圩矿区

贵港大圩矿区工程样本分布参见图14。

图14 大圩矿区工程样本分布

利用前述方法计算和拟合得到的含矿率和Al2O3变异函数分别见图4和图15。含矿率变程为600m，Al2O3品位变程为800m。从地质统计学规律考虑，大圩矿区探求333资源量的工程间距600m就能满足要求；探求332资源量工程间距为300m；探求331资源量工程间距为150m。

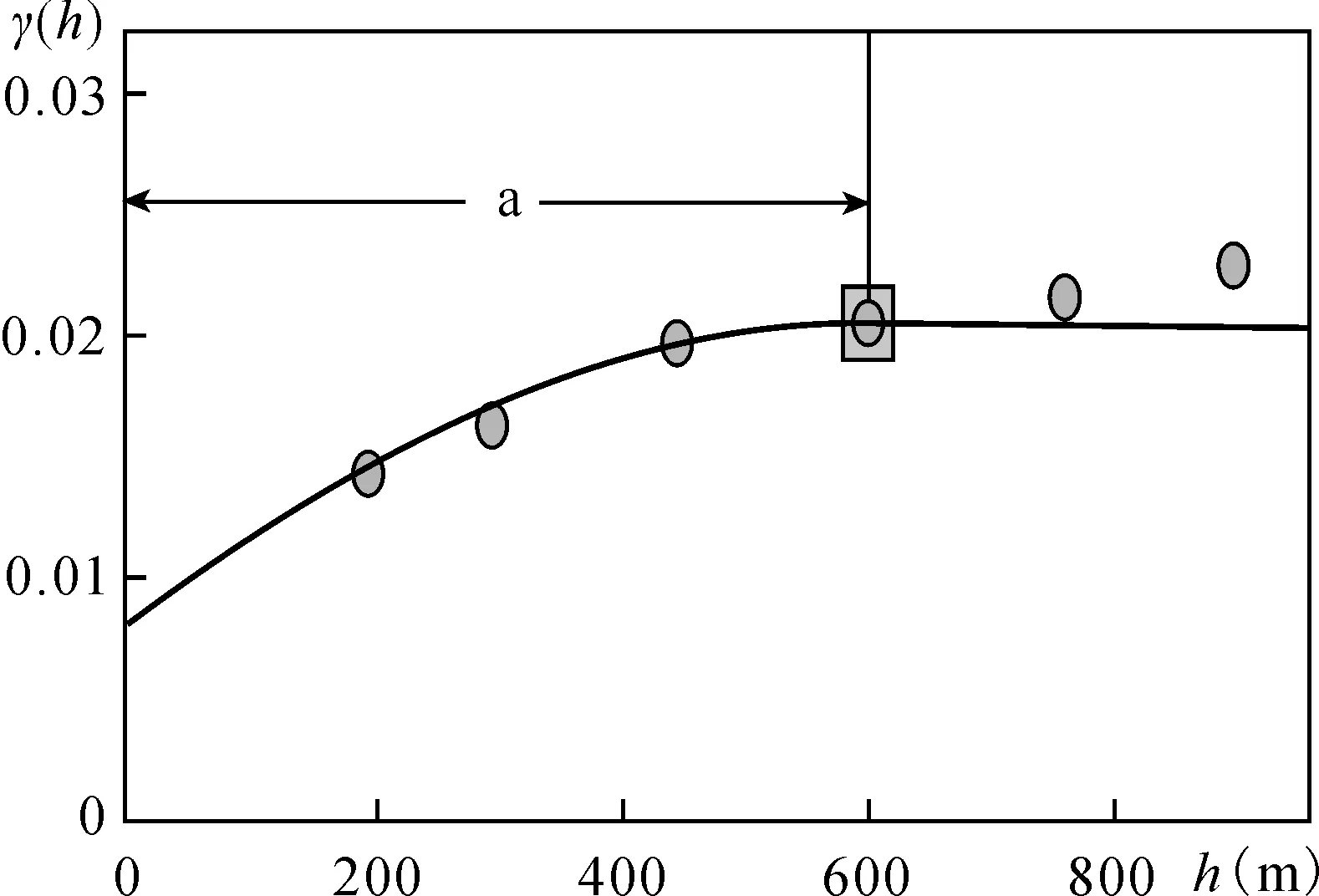
图15 大圩矿区含矿率变异函数

在缺乏地质统计学数据分析的情况下，上述三个矿区普查阶段设计的工程间距均为200m。通过地质统计学规律分析，马岭矿区工程控制程度达到普查要求；邓保矿区和大桥矿区则达到了详查的要求，在200m工程间距下可以估算332资源量。这可避免地质规范千篇一律式的生搬硬套，节约勘查成本，提高勘查效率。

4 矿体边界和资源类别的自动划分方法

对于没有明显自然边界的红土风化型铝土矿床、风化残余型高岭土矿床、风化壳离子型稀土矿床、风化淋滤型镍矿床等，矿体边界的划分一般根据工程揭露结果人工圈定。利用地质统计学方法，结合矿床模型的矿层顶、底板界面在垂直方向上的边界控制，这类矿床的矿体边界完全可以在资源量分类和估算过程中自动圈定。

国内传统资源量分类一般采用“工程网度法”，工程网度法直观，便于人工复制，但不适合于电脑的自动分类估算。地质统计学方法一般采用变程范围内的见矿样品密度进行资源储量类别的划分(侯景儒等，1980，2001；罗周全等，2007)，适合于自动化处理。从地质统计学角度看，区域化变量变异函数变程范围内的地质情况是规律可知的，超出变程以外的地质情况则是不确定的，在确定资源量的各个变量的变程范围内进行资源量的分类和估算更符合各矿区的地质规律，其结果更可靠。

根据国内外的经验，结合地质统计学规律，在桂中三水铝土矿资源量估算中我们研究采用如下的资源量自动化分类方法：如在离矿块中心点1/4变程范围内有3个工程控制，则该矿块的资源量为探明的资源量331；如在离矿块中心点1/2变程范围内有3个工程控制，则该矿块的资源量为控制的资源量332；如在离矿块中心点1个变程范围内有3个工程控制，或在离矿块中心1/2变程范围内有2个工程控制，或在离矿块中心1/4变程范围内有1个工程控制(平推四分之一原则)，则该矿块的资源量为推断的资源量333；不符合上述条件或估值品位达不到工业指标要求的区块为无矿区块，以此实现各类别资源量的自动分类和有矿区与无矿区的自动划分。马岭矿区矿体边界自动划分和资源类别自动分类结果见图16。

图16 马岭矿区矿体边界和资源量类别分布图

5 资源量的自动化估算方法

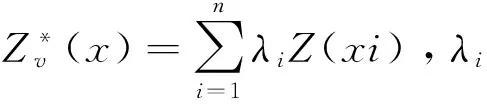
表1 桂中主要矿区资源量估算结果Table 1 Estimations of resources for primary mines incentral Guangxi

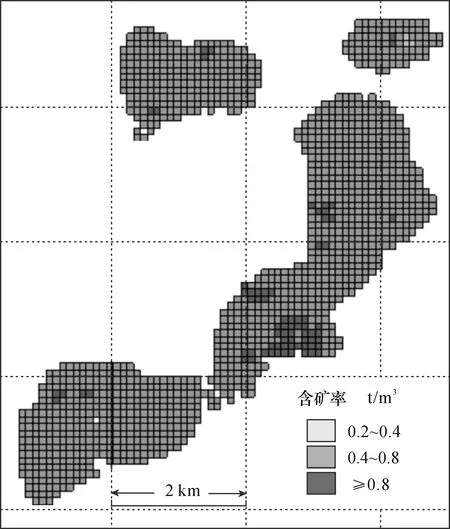
图17 马岭矿区含矿率分布图

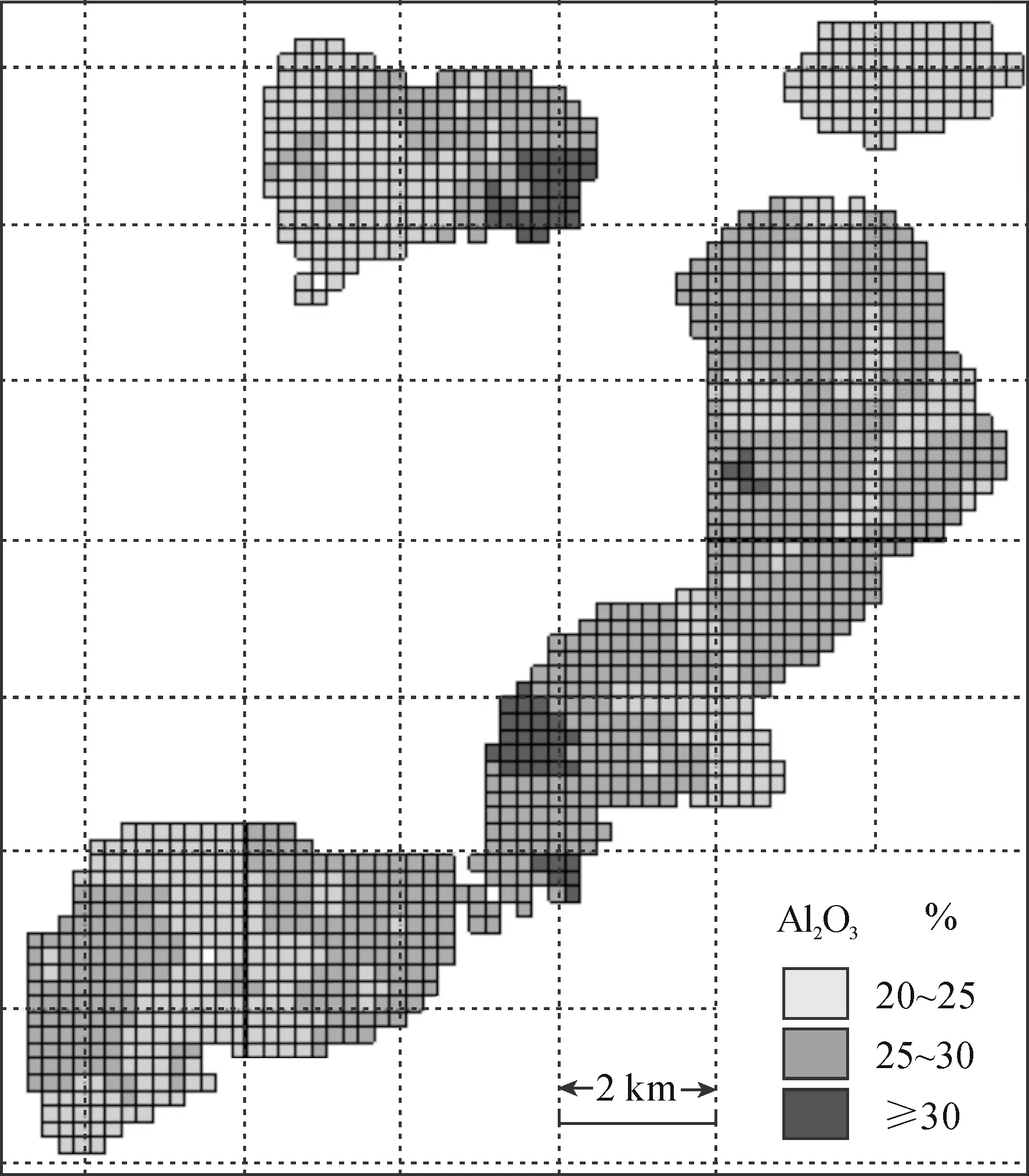
图18 马岭矿区Al2O3品位分布图

6 结论

对勘查工程样本数据进行含矿率和品位的地质统计学分析，由变异函数的变程确定各矿区(体)合理的勘查工程间距和资源量分类估算方案，可极大地提高勘查和资源评价的效率和精度。地质统计学资源量分类的“影响范围+工程密度” 方法集中了“样品密度法”和“工程网度法”两者的优点，比传统的“勘查类型+工程网度” 法更科学、更符合具体矿床的变化规律，不仅能快速而准确地自动分类和估算各类别资源量，还能自动地确定矿体的边界，值得在桂中三水铝矿床下一步勘查和资源评价中推广使用；对其他地区的风化红土型三水铝矿床和风化离子型稀土矿床的勘查评价也具有借鉴意义。

Blais，R A，Carlier，P A.1968.Applications of geostatistics in ore evaluation [J].Canadian Institute of Mining and Metallurgy Special，9:41-68

Chen Jian-gong，Deng Shun-hua，Wang Li-guan.1994.Calculation and fitting of 3D variogram [J].Journal of Central-South Institute of Mining and Metallurgy,22(6)：686-690(in Chinese)

D.D.Sarma.2002.Geostatistics with applications in earth sciences[M].New Delhi:Capital Publishing Company:78-94

Deng Jun.2006.Geological characteristics and control factors of gibbsite deposits in Central Guangxi [J].Sourth land and resources，23(3)：21-23(in Chinese)

Hou Jing-ru，Huang Jing-xian.1980.Applications of geostatistics in reserves estimation of Dexing copper mine [J].Geology and Exploration，16(12)：42-48(in Chinese with English abstract)

Hou Jing-ru，Huang Jing-xian.2001.Application of geostatistics in classification for resources/reserves of solid fuels and mineral commodities[J].Geology and Exploration，37(6):62-67(in Chinese with English abstract)

Hou Jing-ru，Zhou Qiu-lan，Zhang Yu-heng，Huang Shi-qian.1978.Kriging for grade estimation of ore block in Geostatistics [J].Geology and Exploration，14(3)：88-95(in Chinese)

He Shao-yuan.1975.Several geostatistical models[J].Geology and Exploration，11(6):69-74(in Chinese)

Lu Yuan-qing，Wang Guo-qing，Qin Quan-guang.2007.Gibbsite deposit characteristics and utilization evaluation in Central Guangxi[J].Sourth land and resources，24(9)：33-35(in Chinese)

Luo Zhou-quan，Liu Xiao-ming，Wu Ya-bin，Liu Wang-ping，Yang Biao.2007.Application of geostatistics in polymetallc deposit reserves calculation[J].Geology and Exploration，43(3)：86-90(in Chinese with English abstract)

R.A.Price，P.A.Karlie，He Shao-yuan.1975.Application of geostatistics in deposit exploration [J].Geology and Exploration，11(3)：81-84(in Chinese )

Wang Rui-hu，Li Mei.2011.Metallogenic Characteristics，Prediction of Total Mineral Resources and Development Prospect for High-Iron Gibbsite-Type Bauxite Ore in Central Guangxi[J].Journal of Guilin university of technology，31(2)：169-176(in Chinese with English abstract)

Xing Hong-xing，Ju Da-zhong，Lin Jian-yang.1997.The ordingary krging’s application to mineral calculation of reserves [J].Geology and Exploration，33(4)：46-51(in Chinese with English abstract)

Xu Jun-long,Wen Xing-ping,Yu Min,Li Chao,Wang Jun,Zhang Li-juan,Zhou Yang,Qiao Xu.2014.An analysis of linear structures in the Huize Lead-zinc mine based on remote sensing images using the principle of geostatistics [J].Geology and Exploration,50(4)：0763-0771(in Chinese with English abstract)

[附中文参考文献]

陈建宏，邓顺华，王李管.1994.三维变异函数的计算和拟合[J].中南矿冶学院学报，22(6)：686-690

邓 军.2006.桂中三水铝土矿地质特征及控矿因素浅析[J].南方国土资源，23(3)：21-23

侯景儒，黄兢先.1980.地质统计学在德兴铜矿储量计算中的应用[J].地质与勘探，16(12)：42-48

侯景儒，黄兢先.2001.地质统计学在固体矿产资源/储量分类中的应用[J].地质与勘探，37( 6)：62-67

侯景儒，周秋兰，张玉衡，黄世乾.1978.地质统计学中估计矿块品位的克里格法[J]，地质与勘探，14(3)：88-95

何绍渊.1975.几种地质统计模型[J].地质与勘探，11(6)：69-74

卢元庆,王国清,覃全光.2007.桂中高铁三水铝矿矿床特征及开发利用评价[J].南方国土资源，24(9)：33-35

罗周全，刘晓明，昊严斌.2007.地质统计学在多金属矿床储量计算中的应用研究[J].地质与勘探，43(3)：86-90

R.A.伯赖斯,P.A.卡尔里,何绍渊.1975，地质统计学在矿床勘探中的应用[J].地质与勘探，11(3)：81-84

王瑞湖,李 梅.2011.桂中高铁三水铝土矿成矿特征、资源总量预测与开发前景[J].桂林理工大学学报，31(2)：169-176

邢红星，琚大忠，林建阳.1997.普通克里格法在矿产储量计算中的应用[J].地质与勘探，33(4)：46-51

徐俊龙,温兴平,余 敏,李 超,王 军,张丽娟,周 杨,乔 旭.2014.基于地质统计学原理的会泽铅锌矿遥感线性构造解析[J].地质与勘探,50(4)：0763-0771

(GuangxiNo.274GeologicalExplorationTeam，Beihai，Guangxi536005)

Application of Geostatistics in Exploration and Evaluation of Gibbsite

Deposits in Central Guangxi Province

HUANG Guo-you，LU Guang-hui，LIN Zui-jin，GOU Xiao-li

The gibbsite deposits in central Guangxi Province are the unique large-scale gibbsite deposits in China with mineral resources of 770 million tons confirmed initially.This paper presents the applications of the geostatistics method to exploration and resource evaluation of this deposit，including the calculation and fitting of the variograms of typical gibbsite deposits，determining the best exploration project spacing using the variograms;automatic classification of resources and estimation of resource amount.

gibbsite，geostatistics，variogram，exploration and evaluation，estimation of resource

2016-01-08；

2016-04-24；[责任编辑]陈伟军。

黄国有(1965年-)，男，高级工程师，学士，地质矿产方向。E-mail:cnperson@126.com。

P618

A

0495-5331(2016)04-0751-08

Huang Guo-you,Lu Guang-hui,Lin Zui-jin,Gou Xiao-li.Application of geostatistics in exploration and evaluation of gibbsite deposits in central Guangxi Province[J].Geology and Exploration,2016,52(4):0751-0758.