利用方格网法计算复杂地形开挖土方量
2016-12-28曾怀恩
曾怀恩,葛 奎
(1.三峡大学 三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002;2.湖北省水电工程施工与管理重点实验室(三峡大学),湖北 宜昌 443002;3.水电工程智能视觉监测湖北省重点实验室,湖北 宜昌 443002;4.三峡大学 科技学院,湖北 宜昌 443002)
利用方格网法计算复杂地形开挖土方量
曾怀恩1,2,3,葛 奎4
(1.三峡大学 三峡库区地质灾害教育部重点实验室,湖北 宜昌 443002;2.湖北省水电工程施工与管理重点实验室(三峡大学),湖北 宜昌 443002;3.水电工程智能视觉监测湖北省重点实验室,湖北 宜昌 443002;4.三峡大学 科技学院,湖北 宜昌 443002)

介绍了在地形复杂,特别是开挖后地形仍较复杂的条件下,采用方格网法计算开挖土方量的方法。首先简单分析了不准确的开挖边界线对土方量计算结果的影响;然后针对目前软件一般不提供复杂地形开挖边界线的情况,提出了基于网格化处理的确定开挖边界线的简单方法。该方法已应用于某农场土方工程中,取得了较好效果,可为其他类似工程土方计算提供借鉴。
复杂地形;开挖土方量;方格网法;开挖边界线;网格化处理
工程建设中,通常要进行土(石)体开挖,使开挖整理后的地形符合建设需要,如整理成水平面或一定坡度的倾斜面。开挖前,需要测绘工程区域原貌地形图,估计开挖土方量,为工程规划设计和造价预算服务。因开挖施工的偏差,开挖后的地形往往与设计的水平面或倾斜面存在一定的差异,有必要对开挖后的地形进行测绘,准确计算开挖土方量,为开挖工程款结算提供依据。目前,土方量计算方法较多,如DTM法、方格网法、等高线法和断面法等,前两 种方法较常用,各方法计算原理及其适用范围见文献 [1]~[4]。为了提高工作效率,综合上述土方计算方法的软件(如南方CASS软件)应运而生。相比DTM法,方格网法在复杂地形情况下精度略低,但在成果表达方面更清晰明了,且计算结果可简单复核[5],从而更受青睐。在地形复杂,特别是开挖后地形仍较复杂的条件下,利用方格网法可获得较可靠的开挖土方计算结果(许多工程只需要挖方量,而不需要填方量来结算土方工程款),一般通过两期(开挖前、开挖后)土方量求差法得到:假设两期测量的地形都开挖到同一水平面(水平面高度低于开挖范围的最低高程),将计算出的开挖方量求差即得出两期之间的开挖土方量。此时,若开挖边界线确定不够准确,必然引起开挖方量计算的偏差,因此,开挖边界线的严格确定是很有必要的。目前,难以找到能确定两期(开挖后地形非设计平面或倾斜面)之间土方开挖边界线的软件,鉴于此,本文提出了一种确定两期之间土方开挖边界线的方法,并通过实例应用验证了该方法的正确性和可靠性。
1 不准确开挖边界线的影响
通过开挖前与开挖后地形图的对比,可确定开挖边界线(零线)。若开挖后地形为平面(设高程为H1),在开挖前原始地形图上绘高程为H1的等高线即为开挖边界线。但是通常开挖后的地形不是严格的平面,由于目前常用软件不具备提供开挖边界线功能,这时一般是在原始地形图上展绘开挖后采集的高程点,通过原始地形图上等高线与开挖后高程点信息,人工圈定开挖边界线。这种人为确定的开挖边界线必然不够准确,会影响两期土方量求差法计算开挖土方量。例如,最简单的两个情形,即确定的开挖边界线范围比实际开挖边界线范围小或大,如图1所示,图中V1为开挖边界线1范围内的开挖土方量,V2为开挖边界线1与实际开挖边界线围成范围内开挖土方量,V3为实际开挖边界线与开挖边界线2围成范围内的填方量。显然,当确定开挖边界线范围比实际开挖边界线范围小时实际开挖土方量V=V1+V2>V1;对于确定开挖边界线 2,两期土方量求差法计算土方量=V-V3,所以确定开挖边界线范围比实际开挖边界线范围大时计算结果也比实际的小。对于确定的开挖边界线与实际开挖边界线有重叠区域的情形,土方量计算结果肯定会有偏差,但难以评定。
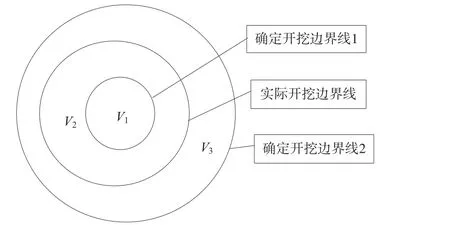
图1 确定开挖边界线比实际开挖边界线范围小或大的影响
2 确定复杂地形开挖边界线的方法
由于野外采集数据在空间分布上的不规则性,难以从两期观测数据对比中准确确定开挖边界线。为此,需要先对两期观测数据分别进行网格化处理,再通过两期间网格点高程的变化来反映填挖厚度,最后可利用网格化数据绘制填挖厚度为零的曲线,即确定了两 期间土方开挖边界线。
空间数据的网格化处理,一般利用插值方法进行,常见插值方法有三角剖分法、趋势面插值法、反距离加权法、样条插值法和Kriging插值法等[6]。因为考虑了数据点的空间相关性,Kriging插值被认为是最优线性无偏内插估计,在地质、测绘、国土、气象、生态和地震监测等众多领域得到了广泛应用[7-8]。这里,建议采用Kriging插值法进行两期观测数据的网格化处理。
设区域化变量H(x)在一组采样点x1,x2,…,xn上的观测值为H(x1), H(x2), …, H(xn)。区域中某个网格点x0的估计值H(x0)可用采样点观测值的一个线性组合来估计,即
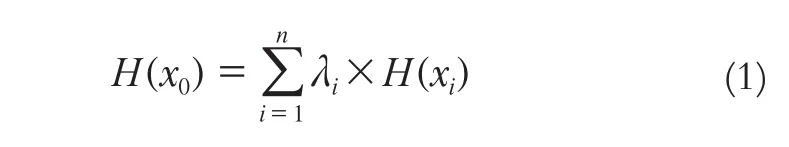
式中,λi为加权系数。如果H(x)满足内蕴假设,依据无偏和最优估计的要求,利用拉格朗日极小化原理,则能建立普通Kriging方程组:
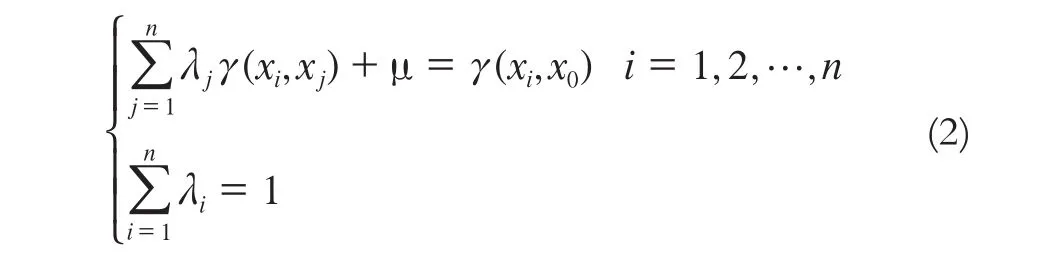
式中,γ(xi,xj)为采样点xi与xj之间的变异函数值;μ为拉格朗日常数。式(2)可改写为如下矩阵形式方程。

则有

由式(4)得到加权系数λi后,将其代入式(1)即可求得网格点x0的估计值H(x0)。
从上述网格点x0插值过程可见,Kriging插值法的关键是变异函数γ(h)的确定(h是空间距离)。γ(h)一般是通过变异函数理论模型(包括线形模型、指数模型、高斯模型和球面模型)拟合实验变异函数曲线得到。实验变异函数γ*(h)为:
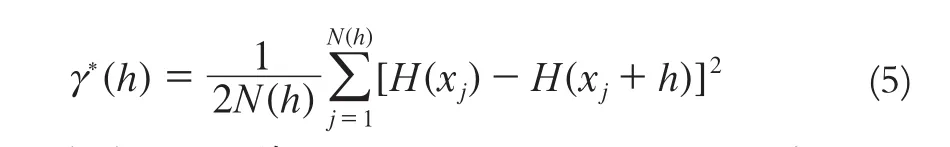
式中,N (h)为距离等于h的点对的数量。以h为横坐标,γ*(h)为纵坐标展绘平面点,即可绘出实验变异函数曲线。该曲线直观地反映了H(x)的空间变异性。变异函数理论模型(如球面模型)可表示为:

式中,a、c0、c和c0+c分别为变程、块金值、拱高和基台值,是模型参数。为了确定理论模型(参数),传统上是依靠人工描图,选取与实验变异函数曲线拟合效果最好的一组参数,但这种做法存在人为因素,结果比较粗糙。为了客观、准确和快速地确定模型参数,笔者采用遗传算法与模式搜索法的综合法,在加权残差平方和最小的标准下,解决了参数的最优化问题,取得了较好效果[8]。
网格化处理时,要求两期数据平面位置范围、网格大小相同,即保证两期网格点平面位移的一致。设开挖前后两期网格点的高程为Hk0、Hk1,k=1,2, …,nk,k、nk分别为网格点点号和总数,则可将相同位置的网格点高程求差得:
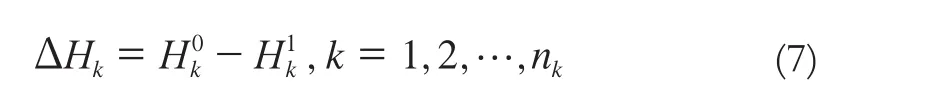
式中,ΔHk反映了网格点k处高程的变化,若为正值,则为开挖高度,若为负值,则为填埋高度,若为零,即为开挖边界点。利用网格化数据文件{ Ek,Nk, ΔHk},k = 1,2,…,nk(Ek、Nk为网格点k的北坐标和东坐标),可以绘制填挖高度等值线,其中值为零的等值线就是两期间开挖边界线,填挖高度为正值的区域为开挖区域,填挖高度为负值的区域为填埋区域。
3 算例分析
某农场地处丘陵地带,地形起伏较大。其第一次土方开挖后,部分区域较平整,而部分区域起伏仍较大,为了准确计算已开挖土方量和为后续土方开挖工程服务,采用GPS RTK技术采集了开挖前后施工区域的坐标数据。将开挖前后施工区域的坐标数据进行网格化处理(网格大小约为20 m×20 m,与数据采集时点密度较接近)和网格点高程求差计算,得到了填挖高度的网格化数据文件,如图2所示,再利用CASS7.0绘制了填挖高度等值线图,确定了开挖边界线,得到了10个开挖块,如图3所示。
图2 填挖高度的网格化数据
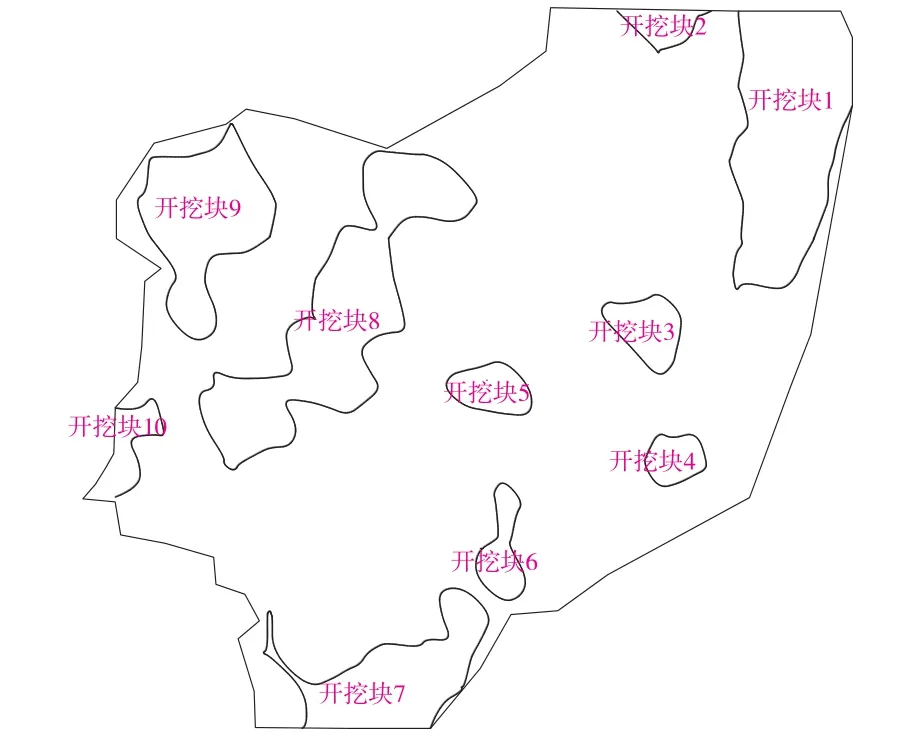
图3 开挖边界线及确定的10个开挖块
在确定了开挖块后,利用CASS7.0方格网法土方计算功能,可快速计算开挖前后两期土方量,计算时假设地形都开挖到同一水平面(水平面高度低于开挖范围的最低高程),通过求差得到实际开挖土方量,计算结果如表1所示。利用CASS7.0 DTM法计算两期间实际开挖土方量为8 765.9 m3,假设它是开挖土方量的理论值,那么本文计算方法所得土方量相对误差为4.2%,可见该方法是正确有效的。需要指出的是,尽管填挖高度的网格化数据也可直接用来计算开挖土方量,但是因为两期观测数据的网格化和求差处理,必然引入了插值模型误差等,使得该方式计算的开挖土方量比直接使用原始数据进行计算的开挖土方量精度要低,因此,本文建议采用后者进行开挖土方量计算。
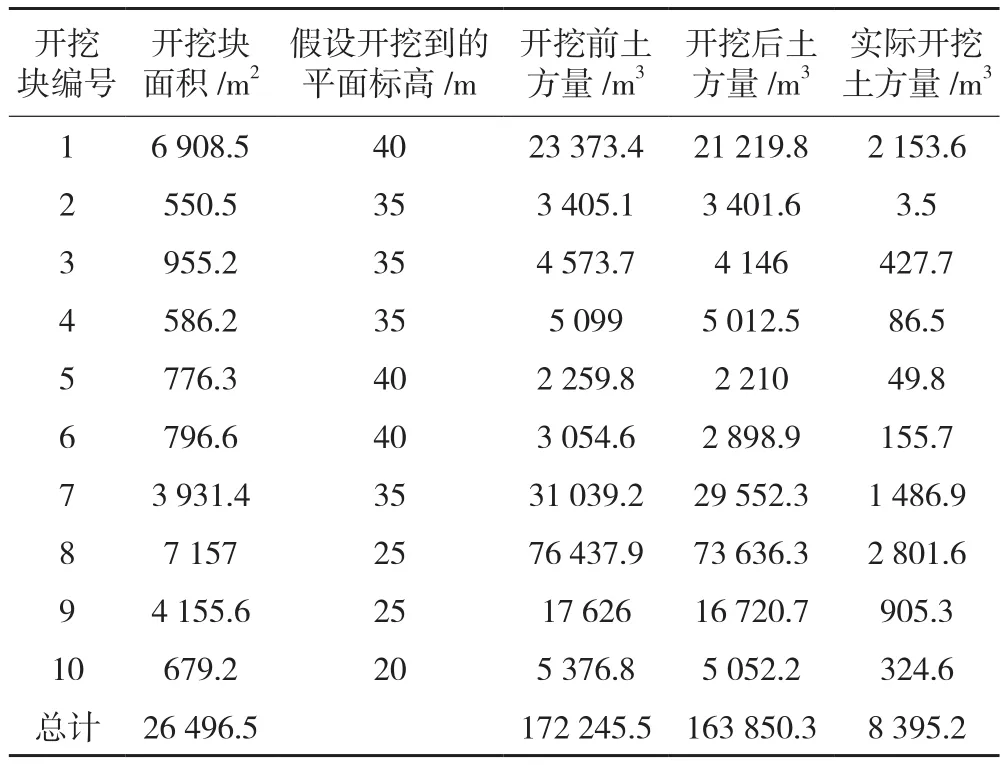
表1 开挖土方量计算表
4 结 语
本文介绍了在复杂地形,特别是开挖后地形仍较复杂的条件下,采用方格网法计算开挖土方量的方法,即假设两期地形都开挖至某一相同高程面,分别求得开挖土方量,然后求差获得实际开挖土方量。这种计算方法,需要严格确定开挖边界线,文中分析了不正确的开挖边界线对土方量计算结果的影响,并提出基于网格化处理的开挖边界线确定方法,通过实际工程应用证实该方法是正确有效的,可为其他类似工程土方计算提供借鉴。
[1] 刘建英.南方CASS软件土方量计算方法的探讨以及特殊地貌土方量的计算[J].城市勘测,2008(5)∶108-115
[2] 冯晓刚,刘明星,撒利伟,等. 三维激光扫描在土石方量精计算中的应用[J].地理空间信息,2015,13(4)∶49-51
[3] 王铁生,程鹏里,赵东保,等.方格网法土方量计算及误差影响[J].测绘通报,2012(增刊)∶109-111,204
[4] 王先鹏,曹荣林.土方量计算的原理与方法及ArcGIS的应用前景[J].地理空间信息,2009,7(4)∶139-141
[5] 李向民.CASS三角网法土方计算的改进[J].矿山测量,2007(4)∶15-17
[6] 曾怀恩.空间数据插值方法及其在填筑碾压检测中的应用研究[J].工程勘察,2013(1)∶48-50,57
[7] 王政权.地统计学及在生态学中的应用[M].北京∶科学出版社,1999
[8] 曾怀恩,黄声享.基于Kriging方法的空间数据插值研究[J].测绘工程,2007,16(5)∶5-8
P258
B
1672-4623(2016)09-0082-03
10.3969/j.issn.1672-4623.2016.09.027
曾怀恩,博士,副教授,主要研究方向为测绘数据处理理论方法、GNSS技术与应用、地质灾害监测与预警等。
2015-08-27。
项目来源:国家自然科学基金资助项目(41104009);精密工程与工业测量国家测绘地理信息局重点实验室开放基金资助项目(PF2015-14);水电工程智能视觉监测湖北省重点实验室开放基金资助项目(2015KLA06);湖北省水电工程施工与管理重点实验室(三峡大学)开放基金资助项目(2014KSD13);2016年湖北省自然科学基金资助项目。
