基于高斯投影的城市独立坐标系参数获取方法

张 黎，舒文强，肖 勇，高 翔，吴国梁

（1.重庆市地理信息中心，重庆 401121）

基于高斯投影的城市独立坐标系参数获取方法

张 黎1，舒文强1，肖 勇1，高 翔1，吴国梁1

（1.重庆市地理信息中心，重庆 401121）

通过获取某城市独立坐标系与国家通用坐标系两个同名点成果，利用高斯投影正算公式对其进行坐标变换，简化成一个关于该独立坐标系中央子午线的一元高次方程；再利用迭代法解算出中央子午线，进而解算参考椭球长半径、北方向偏移量和东方向偏移量等参数，从而实现该独立坐标系与国家大地坐标系之间的成果转换与应用。

城市独立坐标系；参考椭球；高斯投影；中央子午线

随着计算机及信息技术的进步，地理信息产业取得了长足发展，地理信息数据的重要性也日益凸显。我国现有的地理空间信息横向上分布在不同委办局，纵向上又分散在市、区（县）、乡（镇）等，呈现典型的“多重分布”特性。在坐标体系上，我国先后建成了1954北京坐标系、1980西安坐标系和2000国家大地坐标系[1-3]。而在城市规划、建设、管理等实际工作中，多采用城市独立坐标系，因此在地理信息应用过程中，需要通过坐标转换来整合不同空间数据。

目前，坐标转换方法最常用的有四参数和七参数[4-6]。四参数是平面仿射变换，比较简单，但没有考虑椭球体的变形，不能进行大范围高精度的坐标转换。而七参数转换基于参考椭球，理论严谨，转换精度高，控制范围大，但它需要知道各城市独立坐标系的参数，而这些数据涉密，在实际应用中很难获取。因此，在不公布独立坐标系参数的前提下，实现城市独立坐标系和国家通用坐标系间成果的高精度转换具有重大的现实意义。

1 坐标转换原理

1.1 高斯投影

在计算城市独立坐标系参数中，需要利用高斯投影理论[7]进行大地坐标和高斯平面直角坐标间的相互转换：

1）大地坐标（B，L，H）：采用大地纬度B、经度L和大地高程H来描述空间位置的。纬度是空间的点与参考椭球面的法线与赤道面的夹角φ；经度是空间的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角λ；大地高程是空间的点沿着参考椭球的法线方向到参考椭球面的距离，如图1所示。

2）高斯平面直角坐标（x，y，H）：x、y为平面坐标，H为大地高程。椭球体中心O在椭圆柱中心轴上，椭球体南北极与椭圆柱相切，并使某一子午线与椭圆柱相切。此子午线称为中央子午线L0。将椭球体面上的点、线按正形投影条件投影到椭圆柱上，再沿椭圆柱N、S点母线割开，并展成平面，即成为高斯投影平面，如图2所示。

图1 大地坐标系

图2 高斯投影

在此平面上，①中央子午线L0是直线，其长度不变形，离开中央子午线的其他子午线是弧形，凹向中央子午线。离中央子午线越远，变形越大。②投影后赤道是一条直线，赤道与中央子午线保持正交。③离开赤道的纬线是弧线，凸向赤道。大地坐标向高斯平面坐标转换，即高斯投影正算公式为：

1.2 城市独立坐标系参数计算

1）利用GPS与城市独立坐标系联测至少两个四等以上控制点，获得至少两个该城市独立坐标系成果（B1， L1，H）和（B2，L2，H）；再利用GPS与国家通用坐标系联测四等以上控制点，得到国家通用坐标系成果（x1，y1，H）和（x2，y2，H）。

2）将高斯投影正算公式简化为：

式中，经差l=L=L0，以弧度为单位。

3）城市独立坐标系椭球的扁率e与国家参考椭球的扁率相同，但是椭球的半径α不同，在这种情况下大地坐标的经度变化ΔL=0，纬度变化ΔB≈0，将（B1， L1， H）和（x1，y1，H），（B2，L2，H）和（x2，y2，H）分别带入式（11）和式（12）整理可得：

式（20）是一个关于L0的一元高次方程。利用高斯迭代算法可解出参数中央子午线L0；将L0代入式（19）可求解参数椭球长半径a；将a、L0分别代入式（15）和式（16）可解出北方偏移量H和东方偏移量I。

1.3 坐标转换参数计算

国家通用大地坐标系参数是已知的，根据§1.2中获得的城市独立坐标系参数，利用（B1，L1，H）和（B2， L2， H），（x1，y1，H）和（x2，y2，H）的两套坐标系成果，基于Bursa七参数转换模型，计算坐标转换参数。

Bursa七参数坐标转换模型为：

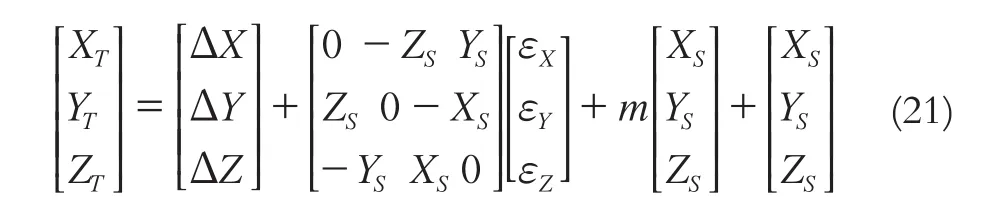
式中，[ΔX ΔY ΔZ]T为3个平移参数；[εXεYεZ]T为3个旋转参数；m为尺度参数。

2 实验研究

为了验证该方法的转换精度，以城市独立坐标系转换为1954北京坐标系为例，计算了其坐标转换精度。

1）测取同名点坐标。利用GPS分别测取8个同名点的1954北京坐标和某城市独立坐标系坐标，如表1。

2）计算坐标参数。利用1、2点成果根据式（15）、式（16）、式（19）及式（20），计算出中央子午线、椭球长半径、北偏、东偏等坐标参数。

3）求取坐标转换参数。利用步骤2）所求的坐标系参数，将1、2、3点成果带入七参数转换模型中，计算得到七参数。

4）转换坐标及精度统计。4、5、6、7、8点成果较差，结果如表2所示。利用该七参数进行坐标转换后的较差最大为0．036 m，完全满足地理信息坐标转换的需要。

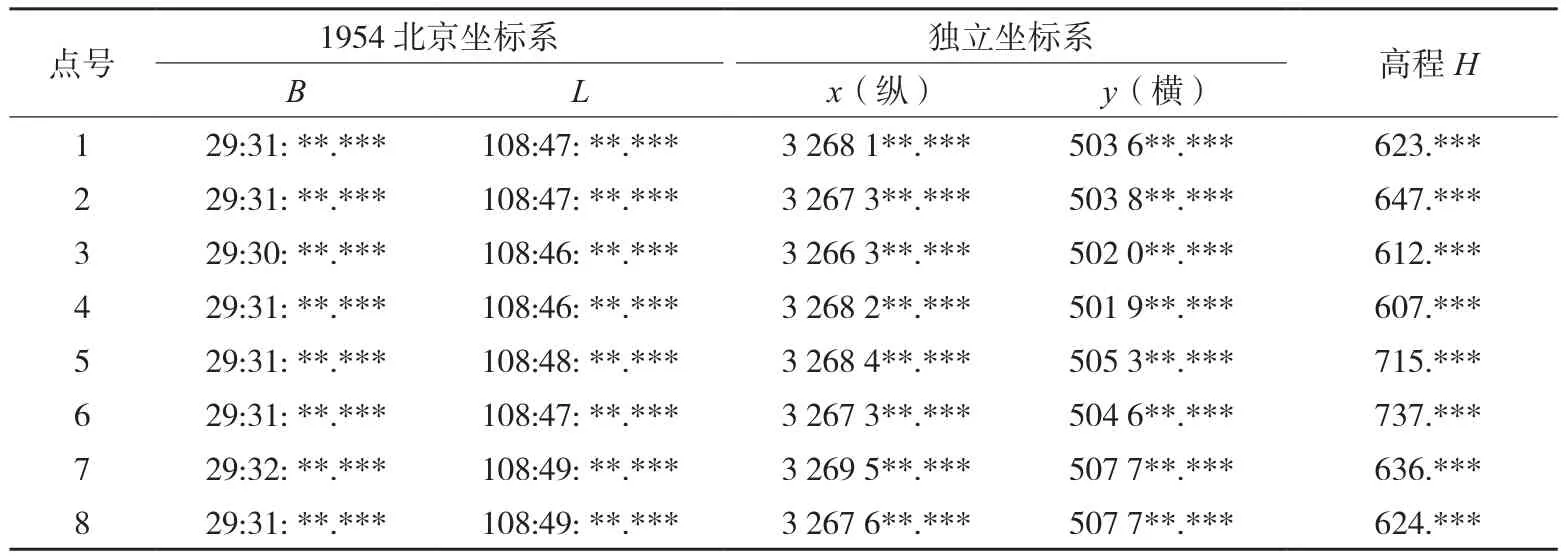
表1 同名点成果表

表2 坐标转换成果较差统计表

3 结 语

本文阐述了一种基于高斯投影的城市独立坐标系参数获取方法，并通过实验证明了该方法既避免了公布独立坐标系参数，又实现了大范围高精度的坐标转换，完全能满足我国地理空间信息坐标转换变形小于2．5 cm/km的要求，具有较高的科研价值和现实意义。

[1] 张项铎,谢世杰．WGS84转换为国家实用坐标的研究[J]．测绘通报,1997(5)∶5-7

[2] 周忠谟,易杰军,周琪．GPS测量原理与应用[M]．北京∶测绘出版社,2004∶31

[3] 陈俊勇．中国现代大地基准∶中国大地坐标系统2000(CGCS2000)及其框架[J]．测绘学报,2008,37(3)∶269-271

[4] 王解先,王军,陆彩萍．WGS84与北京54坐标的转换问题[J]．大地测量与地球动力学,2003,23(3)∶70-73

[5] 方兴,曾文宪,刘经南,等．三维坐标转换的通用整体最小二乘算法[J]．测绘学报,2014(11)∶39-43

[6] 曾怀恩,黄声享．三维坐标转换参数求解的一种直接搜索法[J]．武汉大学学报(信息科学版),2008(11)∶18-21

[7] 朱华统．常用大地坐标系及其变换[M]．北京∶解放军出版社,1990∶8

P282.2

B

1672-4623（2016）09-0071-03

10.3969/j.issn.1672-4623.2016.09.023

张黎，硕士研究生，主要研究方向为GNSS全球导航定位系统及测绘成果质量检查与验收。

2016-05-12。

项目来源：2016年国家基础测绘科技计划资助项目（2016KJ0303）。