震后应急物资配送的模糊定位-路径问题研究

刘长石，彭 怡,寇 纲

(1.电子科技大学经济与管理学院,四川 成都 611731； 2.湖南商学院工商管理学院，湖南 长沙 410205；3.西南财经大学工商管理学院，四川 成都 610074;4.湖南商学院湖南省移动电子商务协调创新中心，湖南 长沙 410205；5.湖南商学院移动商务智能湖南省重点实验室，湖南 长沙 410205)



震后应急物资配送的模糊定位-路径问题研究

刘长石1,2,4,5，彭 怡1,寇 纲3

(1.电子科技大学经济与管理学院,四川 成都 611731； 2.湖南商学院工商管理学院，湖南 长沙 410205；3.西南财经大学工商管理学院，四川 成都 610074;4.湖南商学院湖南省移动电子商务协调创新中心，湖南 长沙 410205；5.湖南商学院移动商务智能湖南省重点实验室，湖南 长沙 410205)

从系统集成优化的角度研究震后应急物资配送的一种新模糊定位-路径问题(LRP)，综合考虑救灾点所在地理位置和地形导致的应急车辆行驶时间的随机性、救灾点应急物资需求量的不确定性与应急物资配送的时间紧迫性，以应急物资总运达时间最短与总配送成本最小为目标，构建一个基于机会约束规划的多目标模糊LRP优化模型，并根据模型的特点设计了一种混合免疫遗传算法予以求解。最后，通过算例验证了本文方法能有效解决震后应急物资配送的模糊多目标LRP，实现了震后应急物流中心定位和应急车辆路径规划的联合决策。

应急物资配送；车辆随机行驶时间；定位-路径问题；混合免疫遗传算法

1 引言

近年来地震灾害频发，给人类带来了巨大的人员伤亡和财产损失。例如2008年5月12日，中国四川省汶川县发生里氏7.8级地震，约6.9万人遇难；2010年1月12日,海地发生7.3级地震，超过27万人死亡；2015年4月25日，尼泊尔发生8.1级地震，造成重大人员伤亡。为尽可能降低地震损失和人员伤亡，应急物资必须在震后尽可能短的时间内配送到各救灾点。通常，震后应急物资配送首先考虑在有限的时间、空间和资源等各种约束条件下将应急物资从各级应急物资储备库运往设置在灾区附近的各应急物流中心，然后再由各应急物流中心配送至各救灾点[1]。因此，应急物流中心定位(Location Allocation Problem, LAP)与应急车辆路径规划(Vehicle Routing Problem, VRP)是震后应急物资配送的两个关键问题。有部分学者采用分别解决LAP与VRP的方法求解LRP[2-3]。事实上，LAP与VRP两者之间存在相互依赖、相互影响的关系。例如，应急物资配送中的不同LAP方案导致不一样的VRP规划，VRP规划结果反过来也会影响LAP方案[4-6]。因此，必须综合考虑应急物资配送中的LAP和VRP的联合决策问题，即定位-路径问题(Location Routing Problem, LRP)。

当前，关于商业物资配送中的LRP研究成果比较多[7-8]，但是关注应急物资配送中的LRP研究文献相对较少。代颖等[9]考虑救援时间范围模糊的LRP，构建了一个以救援时间满意度之和最大、应急物流系统总成本最小为目标的多目标LRP优化模型，并设计了一种混合遗传算法予以求解。孙华丽等[10]考虑了不确定应急物资需求与路网通行能力风险，以系统总成本最小为目标，建立了一个应急物流LRP模型，并设计了一种改进遗传算法求解该问题。Sun Huali等[11]采用双层规划理论，以救援时间满意度最大与系统总成本最小为目标进行了应急物流中的LRP规划。Han Yunjun等[12]考虑时间窗和道路容量限制的LRP，采用拉格朗日松弛法将其转化为LAP与VRP分别予以解决。李双林等[13]研究了震后初期应急物资配送的模糊多目标LRP，以应急物资总配送时间最短和受灾点应急物资未满足的总损失最小为目标建立了一个多目标LRP优化模型，并设计了一种遗传算法予以求解。Wang Haujun等[14]研究了震后开放式应急物资供应的LRP，构建了一个非线性整数LRP优化模型，并设计了一种混合启发式算法予以求解。最近还有马祖军等[15]研究了带限制期的震后应急物资配送模糊多目标开放式LRP, Rath与Gutjahr[16]研究了灾后应急物资配送中的LRP。

已有研究大多假设救灾点的应急物资需求量小于车辆容量、应急物流中心与救灾点分属两个不同的集合、应急物流网络始终正常连通、车辆在各路段上的行驶速度固定，甚少考虑到救灾点所处的地理位置和地形对车辆行驶时间的影响，同时鲜少考虑灾后的道路桥梁损毁与路网动态恢复等现实情况，难以体现震后应急物资配送的真实特性。在实际的震后应急物资配送过程中，重灾区可能有部分救灾点的应急物资需求量非常大；由于地震灾害的破坏性，应急物流网络可能存在不同损毁程度的部分道路，致使配送车辆通行不畅，导致行驶在损毁道路上的车辆的行驶时间难以确定；救灾点所处的地理位置和地形、单位作业单元所需修复时间、道路性质及恢复难易程度等等因素对车辆行驶时间都具有非常大的影响[18-21]。因为与地震中心距离不同的道路的损毁情况是不同的，不同地形条件下的道路损毁后的抢修难度是有区别的。例如，距离地震中心越近，道路损毁情况越严重；山区道路损毁后的抢修难度要远远大于平原道路损毁后的抢修难度。

基于以上分析，本文研究一种新的LRP：假设震后有n个救灾点，在这n个救灾点内选择m个点作为没有容量限制的应急物流中心，即M⊆N，并综合考虑了救灾点所处地理位置和地形导致的车辆行驶时间的随机性、应急物资需求的不确定性、限制期、车辆多次往返配送、同时进行车辆“满载直配”与“巡回配送”等限制条件，采用机会约束规划理论并以应急物资总运达时间最短和总配送成本最小为目标，构建基于机会约束规划的震后应急物资配送多目标模糊LRP优化模型，并根据模型的特点设计一种混合免疫遗传算法予以求解。

2 多目标模糊LRP数学模型

2.1 问题描述

震后急需在尽可能短的时间、有限的空间和资源约束条件下将应急物资配送到各个救灾点。本文假设地震中心的位置已知，有n个地理位置和地形已知的救灾点，救灾点需求量为一个三角模糊数，在这n个救灾点内选择m个点作为没有容量限制的应急物流中心(该中心必须服务属于自己的那个救灾点)，各应急物流中心拥有多辆不同容量限制的车辆，车辆必须从应急物流中心出发，完成任务后返回到出发点，要求在一定的时间期限内完成所有救灾点的应急物资配送任务。决策问题：确定应急物流中心选址、并规划各物流中心的服务其所分配救灾点的车辆路径，在规定时间期限内满足各救灾点的应急物资需求，使应急物资总运达时间最短、总配送成本最小。

灾区可能有部分救灾点的应急物资需求量非常大，超过车辆容量。因此本文将救灾点分为大需求量救灾点与小需求量救灾点(应急物资需求量大于车辆容量的救灾点为大需求量救灾点，否则为小需求量救灾点)。关于大需求量救灾点采用“需求分割”策略同时进行满载直配与巡回配送。即把大需求量救灾点的应急物资需求分为两部分，先对该大需求量救灾点满足满载直接配送的应急物资需求处理为一个虚拟大需求量救灾点，再对该大需求量救灾点剩余不足最小车辆容量的应急物资需求处理为一个虚拟小需求量救灾点，和其他小需求量救灾点一起进行巡回配送[15]。

2.2 符号说明

定义如下符号和变量：

2.3 模型构建

针对救灾点的模糊需求量必须满足车辆容量限制这一约束条件，本文引进决策者置信水平这一概念，采用概率方法将其处理为机会约束条件，构建震后应急物资配送的多目标LRP模型如下：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

xijk=0,∀(i,j)∈M,∀k∈V

(8)

(9)

(10)

Tkj=Tki+tijkxijk,∀(i,j)∈AN,k∈V

(11)

Tki≤Lti,∀i∈AN,k∈V

(12)

xijk(Tkj-Tki)≥0, ∀(i,j)∈AN,k∈V

(13)

yg={0,1}, ∀g∈M

(14)

βgi={0,1},∀g∈M,i∈AN

(15)

wk={0,1},∀k∈V

(16)

xijk={0,1}, ∀(i,j)∈AN,k∈V

(17)

目标函数(1)表示最小化应急物资总运达时间；目标函数(2)表示最小化应急物资总配送成本(物流中心固定成本、车辆满载直配成本、车辆巡回配送成本、车辆使用固定成本)。约束条件(3)保证分配给巡回配送车辆的所有小需求量救灾点的应急物资需求量之和不超过该车容量的可能性不低于预先确定的置信水平；约束条件(4)表示运到大需求量救灾点的应急物资要满足该救灾点的需求，其中rem(di,Qk)表示该救灾点需求量与应急车辆容量的余数；约束条件(5)保证开设的应急物流中心有车发出；约束条件(6)保证未开设的应急物流中心不能发车；约束条件(7)为车辆路径连续条件，即进入救灾点的车辆必须从该救灾点离开；约束条件(8)保证任意2个应急物流中心不直接相连；约束条件(9)保证应急车辆至多只能分配给一个应急物流中心；约束条件(10)保证每个救灾点有且仅有一辆车进行巡回配送服务；约束条件(11)给出车辆到达救灾点的时间计算方法；约束条件(12)表示救灾点的时间窗约束；约束条件(13)保证车辆路线时间的顺序性；约束条件(14)至(17)为整数变量约束。其中，ceil(fbgi/Qk)表示不小于fbgi/Qk的整数。

2.4 模糊需求量约束条件处理

由于约束条件(3)具有模糊参数di，无法直接计算，需要进行适当处理。本文综合参考了代颖等[6,13,15,17]的模糊需求处理方法。令Ek表示应急车辆k配送完所分配救灾点后的剩余容量，Ek=(Ek1,Ek2,Ek3)，即：

(18)

又

(19)

故约束条件(3)等价于

Pos(Ek≥0)≥ρ,∀k∈V

(20)

2.5 随机行驶时间约束条件处理

研究应急车辆行驶时间的文献甚少。仅仅孙华丽等[10]考虑了应急救援过程中的超期风险、路段通行能力风险、路径复杂性等因素下的车辆行驶时间；Shinozuka等[18]和Bertini等[19]都把道路容量和车辆数量作为影响车辆行驶的关键因素，但都只分析了道路正常状态下的车辆行驶时间；苏幼坡[20]根据灾后道路需要修复的作业单元数、道路性质及恢复难易程度来预计车辆行驶时间；Peng Min等[21]对震后车辆行驶时间进行了模拟仿真。

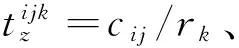
(21)

3 混合免疫遗传算法设计

LRP的求解算法主要分为两阶段求解算法与整体求解算法。前者运行时间较短，后者运行时间相对稍长，但是求得的LRP规划方案较优[7-9]。免疫遗传算法不仅保留了遗传算法的搜索特性，且具有免疫算法的多机制求解多目标函数最优解的自适应特性，能有效避免算法早熟与收敛于局部极值[22,23]。因此，本文基于整体求解的思路，设计了一个混合免疫遗传算法求解LRP。

3.1 算法设计

3.1.1 初始抗体群产生

将LRP的目标函数及约束条件对应于抗原，问题的解对应于抗体，按照预先设定的群体规模H，随机生成一组抗体作为初始抗体群B。

本文中的抗体由三个子串组成：子串1有n个基因位(n为救灾点数目)，每个基因位的取由1到n的自然数随机排列生成且相互不能重复的值；子串2有k个基因位，每个基因位的取由1到m的自然数中随机生成且相互不能重复的值(m为候选应急物流中心数目)；子串3有n个基因位，每个基因位的取值由1到k的自然数中随机选取(k为应急车辆数目)。其中，子串1表示路径中各需求点的排列顺序，子串2表示各应急车辆归属哪一个应急物流中心，子串3和子串1中的基因位一一对应，表示为各救灾点服务的车辆编号。

3.1.2 抗体适应度与亲和力计算

本文LRP模型的目标函数与所有约束条件均为线性函数，可行域是凸集，根据文献[15,25]可知，凸性多目标规划问题可以用加权法处理。因此，抗体适应度函数可通过对目标函数值进行变换得到。

(22)

而且fitness(b)的值越大，抗体b与抗原的亲和力G(b)越大，表明该抗体越优。

3.1.3 抗体促进与抑制

在抗体进化过程中，选择亲和力较高而且浓度较低的抗体进行促进。同时，为确保抗体群体更新过程中抗体的多样性、避免未成熟收敛，本文规定当抗体的浓度达到一定的阀值时随机生成超浓度规模数量的若干新抗体替换旧抗体。根据抗体的编码特点，本文定义抗体b浓度为：

(23)

其中，

如果种群中一共有ε种不同的亲和力，设抗体浓度阀值为ε/H。

3.1.4 遗传操作

采用传统遗传算法的3基本操作方法，即选择、交叉和变异，这里不再累述。

3.1.5 免疫算子

免疫算子一般包括提取疫苗、接种疫苗和免疫选择等3个步骤。

(1)提取疫苗。抽取当前k+1代的最优个体群中的最优个体，同时找到前k代保留下来的最优个体群中的最优个体，把这2条最优个体的基因位的共同特点和有效信息作为疫苗。

(2)接种疫苗。抽取一定概率的带接种的抗体，进行疫苗接种。

(3)免疫选择。对已接种疫苗的个体进行检测，若子代最高适应值的个体优于父代，子代替代父代进入下一种群，否则采用赌轮方式选择父代中的个体进入下一种群。

3.1.6 终止条件

设算法最大迭代次数为M, 当抗体群的进化代数达到了M时算法终止。

3.2 算法复杂度分析

本文算法采用三参数级联编码方式，第一子串长度为n，第二子串长度为m，第三子串长度为n，即每条抗体占用的内存空间为2n+m。如果增加b个救灾点，抗体长度为2(n+b)+m+ω，0≤ω≤b，则每条抗体内存空间的增量为O(2b+ω)。又O(2b)≤O(2b+ω)≤O(3b)，即随着算例增大本文算法占用内存空间呈线性增加。

本文算法的群体规模为H，最大迭代次数为M，问题规模为Q=n+n+k。算法计算时间复杂度分析如下：初始抗体群产生后，每次迭代都要经过适应度计算、抗体促进与抑制、遗传操作、提取疫苗、接种疫苗和免疫选择等计算。混合免疫遗传算法的时间复杂度为：

Ο(H,M,n,n,k)=HΟ(2n+k)+M(Ο(Hn2k)+Ο(HlgQ)+Ο(HlgQ)+Ο(Hn2k)+Ο(Hn2kλ)+Ο(Hn2kλ))≈2HM(Ο(n2k))

其中，λ表示进行疫苗接种抗体的概率。

可见，本文算法的计算量与抗体群规模、迭代次数、需求点数量与车辆数量呈正比。

4 算例分析

以Solomon的VRPTW BENCHMARK PROBLEMS测试数据库中的RC201算例数据为基础，同时根据本文所研究LRP的特点对需求数据进行修改并补充相关数据，产生测试算例。具体方法如下：从RC201数据中随机抽取26个坐标数据作为救灾点的地理位置，救助点之间的距离采用直线距离表示，然后随机产生各救灾点的物资需求数量与地形。候选应急物流中心的是从这26个救灾点内选取使目标函数值最小的3个点。设定各应急物流中心具有2种不同容量类型的车辆。各相关数据如表1与表2所示。

相关变量设置如下：群体规模为40，记忆库容量为10，最大迭代次数为500，交叉概率为0.5，变异概率为0.4,多样性评价函数值为0.95，应急物流中心数量为3，固定使用成本为20000元/个，置信水平为0.9，时间目标函数值的权重w1=0.6，成本目标函数值权重w2=0.4，车辆容量分别为280件与350件，车型1的行驶速度为60km/h,车型2行驶速度为50km/h,平均单位行驶成本为10元/km，地震中心的坐标为(50,50)，Tfp=3，α=5，χ=4，β=3，φ=2。

采用Matlab R2013a对本文设计的混合免疫遗传算法进行编程实现，在AMD A8-4500m APU 1.90GHz、内存4G的微机上对测试算例进行了20次求解。程序运行时间比较短，计算效率比较高，最短计算时间为37.72秒，平均计算时间为38.74秒，最大计算时间为40.76秒。计算结果也比较稳定：20次方案都是启用了12台容量为280件的应急车辆，目标函数值1的最优解为3359.78分钟，最差解为3431.46分钟，前者与后者的差距只有2.09%；目标函数值2的最优解为75093.1元，最差解为76130.6元，前者与后者的差距只有1.36%。选择的3个应急物流中心坐标是：(2,45)、(65,20)、(45,65)。各应急物流中心的最佳车辆行驶路线如图1所示。具体应急物流中心车辆路线安排见表3，车辆路线安排中的数字0表示应急物流中心，其余数字表示救灾点序号。从图1和表3可知，本文的算法有效实现了应急物流中心定位与车辆路径规划的联合决策，合理进行了救灾点的满载直配与巡回配送，在规定时间内完成了应急物资配送任务。

为进一步说明本文方法的有效性，引进阮俊虎等[24]的2个考核指标：平均等待时间、最大等待时间。平均等待时间表示应急物资到达救灾点的平均时间，越短意味着应急物资(尤其是医疗器械与药品)的效用越大。最大等待时间在一定程度上反映了应急物资到达救灾点时间的差距，越短表示应急物资配送越公平[24]。经过计算，本文的混合免疫遗传算法的平均等待时间为108.01分、最大等待时间为259.36分；Yi Wei[3]的蚁群算法的平均等待时间为110.79分、最大等待时间为282.52分。前者的2个考核指标比后者分别降低1.81%与8.19%。说明本文的混合免疫遗传算法具有良好的性能。

在抗体群规模不变的情况下，通过扩展算例1(表1)形成算例2-4,采用本文的混合免疫遗传算法(HIGA)与Yi Wei[3]的蚁群算法(ACA)分别计算各个算例，计算结果如表4所示。表4中，n表示救灾点数量，m表示物流中心数量，k表示车辆数量，计算结果为求解20次的均值。从表4可知，随着问题规模的增大，程序运行时间会有所增加，与前面分析得出的混合免疫遗传算法的时间复杂度2HM(Ο(n2k))一致，且HIGA的计算时间稍优于ACA的计算时间。

表1 救灾点数据

表2 应急车辆数据

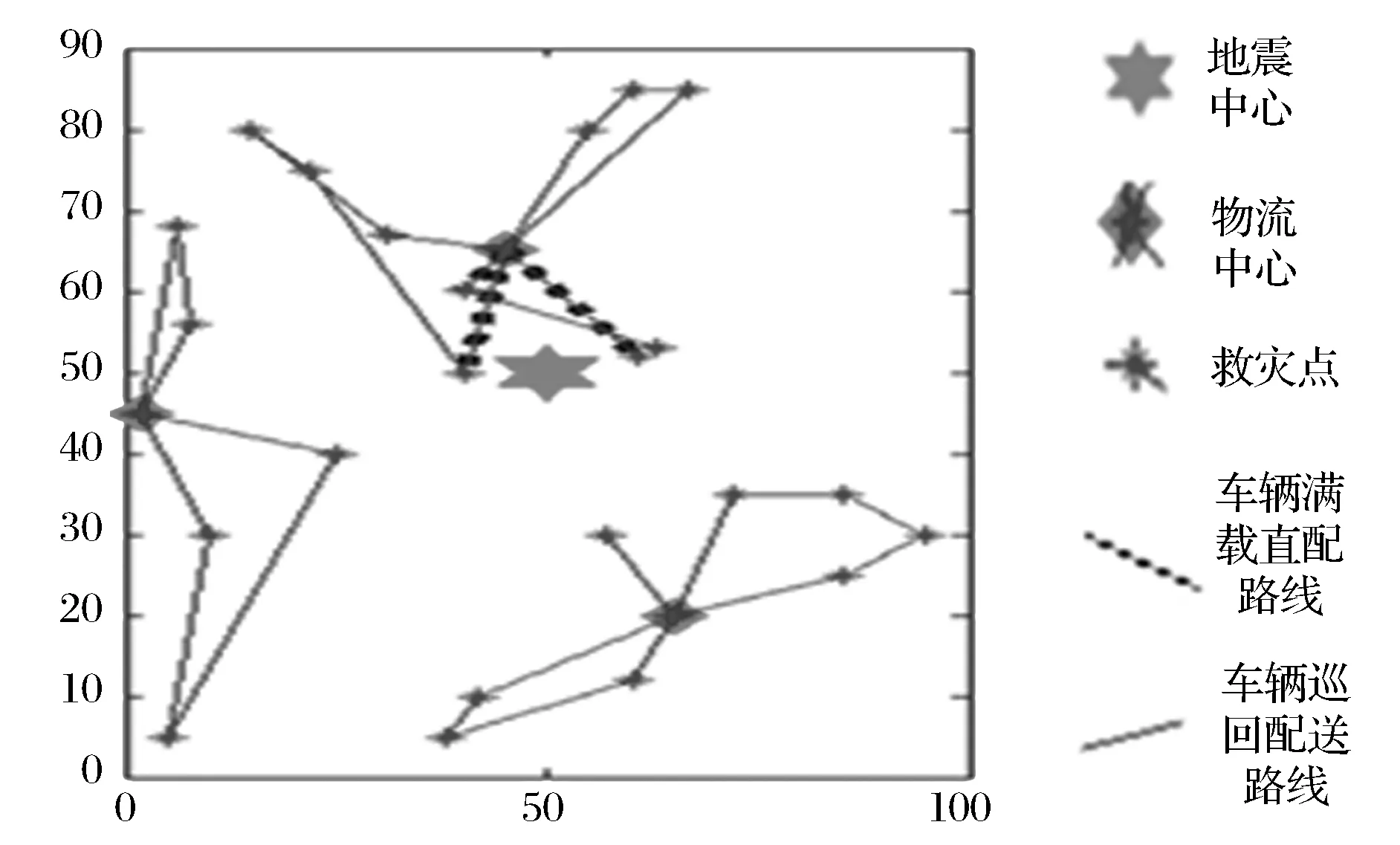
图1 车辆路线安排示意图

表3 应急物流中心车辆路线安排

表4 不同问题规模计算时间

5 结语

震后，为尽可能降低地震带来的人员伤亡与财产损失，应急物资必须在尽可能短的时间内配送到各个救灾点。研究震后应急物流系统、提高应急物资配送绩效，具有非常大的现实价值。本文从系统集成的角度研究了一种新的LRP，并综合考虑了救灾点与地震中心的距离、救灾点的地理位置与地形等因素对车辆行驶时间的影响，构建了一个以应急物资总运达时间最短与总配送成本最小为目标的多目标模糊LRP优化模型，并根据模型的特点设计了一种混合免疫遗传算法予以求解，通过算例验证了本文模型的正确性与算法的稳定性、有效性。

本文构建的模型主要有以下适用条件：在震后应急救援初期，应急物资(尤其是医疗器械与药品)需求不确定、即来即走，从各级应急物资储备库运达各应急物流中心后，马上进行配送安排，救灾点要求应急物资在规定时间内运达，物流中心的车辆与装卸能力充足，应急物流网络存在部分损毁道路；不适合于应急物流中心的应急物资有一定的存储时间这种情况。本文只考虑了单品种应急物资配送的LRP，而现实中的应急物资配送可能涉及多种物资，因此多品种应急物资配送的LRP有待进一步研究。另外，在某些情况下，应急物流具有动态调度的特性，应急车辆路线动态优化也将是下一个研究重点。

[1] 郑斌,马祖军,方涛.应急物流系统中的模糊多目标定位-路径问题[J].系统工程, 2008,27(8):21-25.

[2] Chang M S, Tseng Y L, Chen Jingwen.A scenario planning approach for the flood emergency logistics preparation problem under uncertainty[J].Transportation Research E, 2007,43(6): 737-754.

[3] Yi Wei, Kumar A.Ant colony optimization for disaster relief operations[J].Transportation Research E, 2007,43(6): 660-672.

[4] 曾敏刚,崔增收,余高辉.基于应急物流的减灾系统LRP研究[J].中国管理科学, 2010, 18(2):75-80.

[5] 代颖,马祖军.应急物流系统中的随机定位-路径问题[J].系统管理学报, 2012,21(2): 212-218.

[6] 代颖,马祖军,朱道立,等.震后应急物资配送的模糊动态定位-路径问题[J].管理科学学报, 2012,15(7): 212-218.

[7] 汪寿阳,赵秋红,夏国平.集成物流管理系统中的定位-运输路线安排问题研究[J].管理科学学报, 2000,3(2): 69-75.

[8] 林岩,胡祥培,王旭茵.物流系统优化中的定位-运输路线安排问题(LRP)研究评述[J].管理工程学报, 2004,18(4): 45-49.

[9] 代颖,马祖军,郑斌.突发公共事件应急系统中的模糊多目标定位-路径问题研究[J].管理评论, 2010,22(1): 121-128.

[10] 孙华丽,周战杰,薛耀锋.考虑路径风险的不确定需求应急物流定位-路径问题[J].上海交通大学学报, 2013,47(6): 962-966.

[11] Sun Huali, Wang Xunqing, Xue Yaofeng.A bi-level programming model for a multi-facility location-routing problem in urban emergency system[M]//Zhang Liangchi,Zhang Chunliang.Lecture Notes in Electrical Engineering, 2011,111: 75-80.

[12] Han Yunjun, Guan Xiahong, Shi Leyuan.Optimization based method for supply location selection and routing in large scale emergency material delivery[J].IEEE Transactions on Automation Science and Engineering, 2011,8(4): 683-693.

[13] 李双琳,马祖军,郑斌,等.震后初期应急物资配送的模糊多目标选址-多式联运问题[J].中国管理科学, 2013,21(2): 144-151.

[14] Wang Haijun, Du Lijing, Ma Shihua.Multi-objective open location-routing model with split delivery for optimized relief distribution in post-earthquake [J].Transportation Research Part E, 2014,69: 160-179.

[15] 马祖军,代颖,李双琳.带限制期的震后应急物资配送模糊多目标开放式定位-路径问题[J].系统管理学报,2014,23(5): 658-667.

[16] Rath S, Gutjahr W J.A math-heuristic for the warehouse location-routing problem in disaster relief[J].Computers & Operations Research, 2014,42(2): 25-39.

[17] 张建勇,李军,郭耀煌.模糊需求信息条件下的实时动态车辆调度问题研究[J].管理工程学报,2004,18(4): 69-72.

[18] Shinozuka M, Murachi Y, Dong Xuejiang, et al.Effect of seismic retrofit of bridges on transportation networks[J].Earthquake Engineering and Engineering Vibration, 2003,2(2): 169-179.

[19] Bertini R L, Hansen S, Byrd A,et al.Experience implementing a user service for archived intelligent transportation systems data[J].Transportation Research Record: Journal of the Transportation Research Board, 2005,1917(1): 90-99.

[20] 苏幼坡.城市生命线系统震后恢复过程优化的研究[D].天津:天津大学,2001.

[21] Peng Min, Peng Yi, Chen Hong.Post-seismic supply chain risk management: A system dynamics disruption analysis approach for inventory and logistics planning[J].Computers & Operations Research, 2014,42(1): 14-24.

[22] Molla-Alizadeh-Zavardehi S, Hajiaghaei-Keshteli M, Tavakkoli-Moghaddam R.Solving a capacitated fixed-charge transportation problem by artificial immune and genetic algorithms with a prufer number representation [J].Expert Systems with Applications, 2011,38(8): 10462-10474.

[23] Chui C Y, Kuo I T, Lin C H.Applying artificial immune system and ant algorithm in air-conditioner market segmentation[J].Expert Systems with Applications, 2009,36(3): 4437-4442.

[24] 阮俊虎,王旭坪,杨挺.大规模灾害中基于聚类的医疗物资联合运送优化[J].中国管理科学, 2014,22(10): 80-89.

[25] Ehrgott M,Shao Lizhen,Schobel A.An approximation algorithm for convex multi-objective programming problems[J].Journal of Global Optimization, 2011,50(3): 397-416.

[26] Leyffer S.A complementarity constraint formulation of convex multiobjective optimization problems[J].Informs Journal on Computing, 2009,21(2): 257-267.

Research on Fuzzy Location-routing Problem in Post-earthquake Delivery of Relief Materials

LIU Chang-shi1,2，4，5, PENG Yi1, KOU Gang3

(1.School of Management and Economics, University of Electronic Science and Technology of China, Chengdu 611731, China；2.School of Management, Hunan University of Commerce, Changsha 410205,China；3.School of Business Administration, Southwestern University of Finance and Economics, Chengdu 610074, China;4.Mobile E-business Collaborative Innovation Center of Hunnan Province,Hunan University of Commerce,Changsha 410205, China; 5.Key Laborartory of Huna Province for Mobile Bsiness Intelligence,Hunan University of Commerce,Changsha 410205,China)

In order to improve the efficiency of emergency logistics, a new location-routing problem (LRP) in post-earthquake delivery of relief materials was studied from the view point of integrated optimization.By considering the stochastic vehicle time caused by the location and topography of relief points, the urgent window constraints, the fuzzy demands of relief materials and the urgency of rescue time in post-earthquake, a chance-constrained programming model for the fuzzy LRP was developed, and the goal is to minimize the total time in delivering relief materials and the total costs.A hybrid immune genetic algorithm was proposed to solve the model．Finally，the feasibility and validity of the model and algorithm was demonstrated by a numerical example．The test data are obtained from the Solomon’s VRPTW BENCHMARK PROBLEMS.The results show that the proposed approaches effectively solve the fuzzy multi objective LRP, and realize joint decision of emergency logistics center location and emergency vehicle routing planning.

delivery of relief materials；stochastic vehicle travel time；location-routing problem；hybrid immune genetic algorithm

1003-207(2016)05-0111-08

10.16381/j.cnki.issn1003-207x.2016.05.013

2014-08-17；

2015-10-10

国家自然科学基金面上资助项目(71173028)；国家自然科学基金资助项目(71222108);湖南省教育厅优秀青年项目(15B131);湖南省科技厅重点研发计划项目(2015ZK3049)

简介：刘长石(1975-)，男(汉族)，湖南邵阳人，电子科技大学经济与管理学院博士究生，湖南商学院教师，研究方向：应急物流管理、供应链管理，E-mail:liuchangshi964@126.com.

F252

A