太子河流域降水演变特征浅析

赵志勇，国洪琴

(辽宁省葫芦岛水文局，辽宁葫芦岛 125000)

太子河流域降水演变特征浅析

赵志勇，国洪琴

(辽宁省葫芦岛水文局，辽宁葫芦岛 125000)

文章以太子河流域本溪水文站1952—2014年降水数据为依据，综合应用气候倾向率分析、模比系数差积曲线对太子河流域降水量多年变化特征进行了研究，分析出本溪水文站降水量变化趋势；汛前、汛期降水量演变特征，为本溪水文站乃至太子河流域的中长期降雨预报奠定基础。

降水演变规律；降雨预报；本溪水文站；太子河流域

1 资料与方法

以厄尔尼诺现象为主的气候变化对人类的生存环境和社会经济产生了深远的影响，其中，对降水量的影响尤甚。辽河支流太子河流域是东北地区重要的经济增长地区，其降水量的变化趋势也是水利科学研究的重点方向之一。

1.1 流域气候概况及资料来源

太子河发源于本溪县东草帽顶子山，本溪境内河长168 km，流域面积4 428 km2，河道比降约80%左右。太子河流域多年平均降水量为824 mm，年内降水量分布不均，多集中在汛期6—9月份。太子河流域多年平均水资源量为14.48亿 m3，开发利用率为22.75%，主要集中在本溪市太子河下游地区。

本溪水文站是太子河控制站，设立于1933年11月，位于本溪市平山区体育街，集水面积4 324 km2，至河口距离252 km。

文章分析资料来源于太子河流域本溪水文站1952—2014年逐月降水资料，采用降水倾向率法和累积距平法进行分析，并采用Mann—Kenddall法进行趋势检验。

1.2 降水倾向率法

降水量的长期趋势变化，用线性回归方程表示：式中：P为降水量，mm；a1=dP/dt为线性趋势；a0为常数。

1.3 模比系数差积曲线法

模比系数差积曲线可以反映一段时期内降雨的变化趋势。其公式为：

式中：LPi为距平累计值；xi为第 i年的时间序列值为所计算时间序列的多年平均值。

1.4 Mann—Kenddall检验

Mann—Kenddall的检验方法是非参数方法。非参数检验方法亦称无分布检验，其优点是不需要样本遵从一定的分布，也不受少数异常值的干扰，更适用于类型变量和顺序变量，计算也比较简便。

由于最初由曼（H.B.Mann）和肯德尔（M.G. Kendall）提出了原理并发展了这一方法，故称其为曼—肯德尔（Man—Kendall）法。但是，当时这一方法仅用于检测序列的变化趋势。后来经其他人进一步完善和改进，才形成目前的计算格式。下文采用该方法进行检验。

方法概述：

对于具有n个样本量的时间序列X，构造一秩序列：

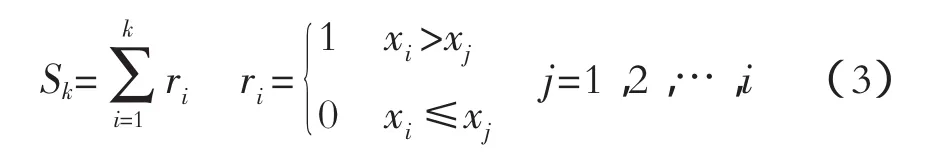
可见，秩序列Sk是第i时刻数值大于j时刻数值个数的累计数。在时间序列随机独立的假定下，定义统计量：

式中：UF1=0，E Sk()，Var Sk()是累计数Sk的均值和方差，在x1，x2，…，xn相互独立，且有相同连续分布时，它们可由式（5）算出：

2 降水量变化趋势分析

2.1 降水倾向率法

2.1.1 年降水趋势分析

根据降水倾向率法对本溪站降水量的变化趋势进行了分析，见图1（a）。降水倾向率b（mm/10 a）取10 a，当b＞0时，说明降水随时间t呈上升的趋势；当b＜0时，说明降水随时间t呈下降的趋势。

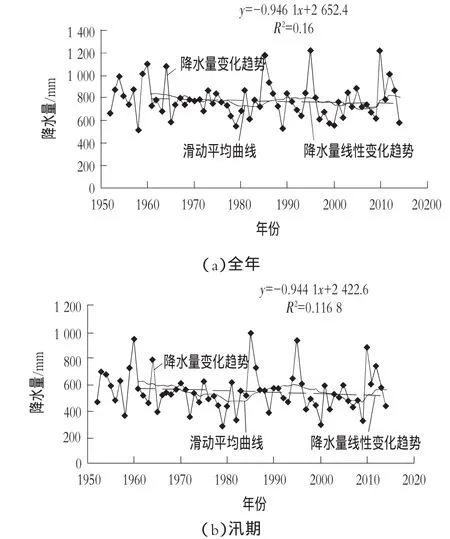
图1 本溪水文站年降水倾向率图

利用Mann—Kenddall法对本溪水文站多年平均降水量进行趋势检验，给定显著性水平α= 0.05，即U0.05=±1.96，趋势检验结果表明：本溪站多年平均降水量1960—1985年有明显下降的趋势，1985—1995年有缓慢上升的趋势，1995—2014年又有下降的趋势。10年滑动平均曲线表示本溪站的降水倾向率为9.461 mm/10 a，R2=0.16。

2.1.2 汛前和汛期降水变化趋势

现将1月1日至5月31日划为汛前，6月1日至9月30日划为汛期。利用Mann—Kenddall法对本溪水文站汛前和汛期降水量进行趋势检验，给定显著性水平α=0.05，即U0.05=±1.96。降水变化趋势检验结果表明：

1）汛前：本溪站汛前1973—1990年有缓慢上升的趋势，2000—2006年有下降的趋势，其余年份变动不明显。根据UF和UB曲线交点的位置，确定本溪水文站降水量减少是一突变现象，具体是从1990年开始的。10年滑动平均曲线表示本溪站汛前的降水倾向率为0.135 mm/10 a，R2=0.000 3。

2）汛期：由于本溪水文站汛期的降水量占全年降水量的比重较大，因此汛期降水量的变化趋势与多年平均降水量的变化趋势相似，见图1（b）。由此可见，本溪站汛前降水量，1960—1985年有明显下降的趋势 ，1985—1995年有缓慢上升的趋势，1995—2014年又有下降的趋势。10年滑动平均曲线表示本溪站的降水倾向率为9.441 mm/10 a，R2=0.116 8。

2.2 年降水模比系数差积曲线法

2.2.1 年降水量周期性分析

对1952—2014年逐年降水量做模比系数差积曲线，由图2（a）可以看出，年降水量变化大体可分为两个时期，在20世纪50年代至70年代中期，总体上是增加的趋势，70年代中期以后呈现周期震荡减少的趋势。

2.2.2 汛前和汛期降水变化趋势

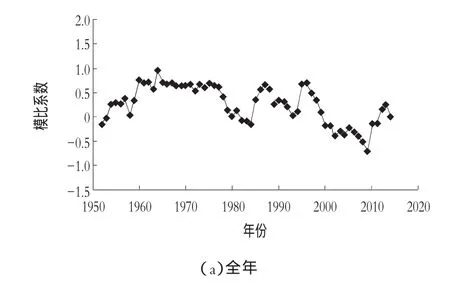
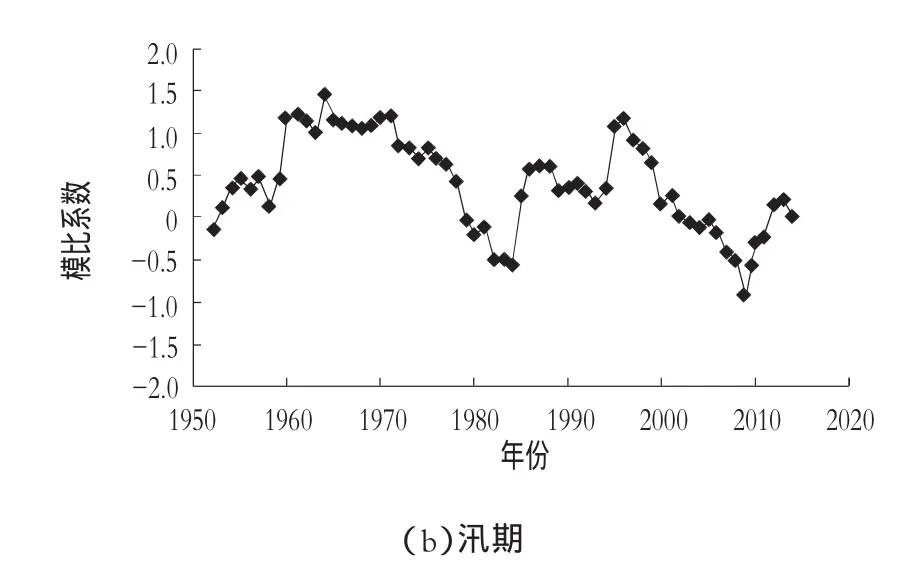
图2 本溪水文站模比系数差积曲线图

对本溪站1952—2014年汛前和汛期降水量做模比系数差积曲线分析，汛前降水量变化大体可分为3个时期，从20世纪50年代至60年代初呈现周期震荡下降的趋势，60年代至80年代中期呈现周期震荡上升的趋势，90年代中期以后呈现周期震荡下降的趋势。

汛期降水量变化大体可分为3个时期，从20世纪50年代至60年代中期呈现周期震荡上升的趋势，80年代中期至90年代中期又呈震荡上升的趋势，90年代中期以后呈现周期震荡下降的趋势。

3 结 论

以降水倾向率和模比系数差积曲线方法分析多年降水变化趋势，并用Mann—Kenddall检验方法对分析结果进行趋势检验，是我国近年来主要采用的方法。该方法经过多次实践，理论成熟、精度较高。

根据上述方法得出的降水量多年变化趋势，在太子河流域中长期降水量预报中得到应用，效果较好，为今后的防汛抗旱、减灾避险等提供了数据基础。

［1］栾兆擎，章光新，邓伟，等.三江平原50年来气温及降水变化研究［J］.干旱区资源与环境，2007，21（11）：39-43.

［2］张雪花，步新影，孔繁德.气候变化对秦皇岛地区降水量影响分析［J］环境科学与管理，2007，32（8）：62-64.

［3］张剑明，黎祖贤，章新平.长沙近50年来降水的多时间尺度分析［J］.水文，2007，27（4）：78-80.

P337

A

1002－0624（2016）12－0033－03

2016-07-24