隔声量计算的边界元-有限元-统计能量法

石嘉欣，杨德庆，郁 扬

（上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，高新船舶与深海开发装备协同创新中心，上海 200240）

隔声量计算的边界元-有限元-统计能量法

石嘉欣，杨德庆，郁 扬

（上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，高新船舶与深海开发装备协同创新中心，上海 200240）

提出边界元-有限元-统计能量（BEM+FEM+SEA，简称BFS）混合方法模拟驻波管，即BFS驻波管模拟法，计算材料的隔声量。探究了不同边界条件对BFS驻波管模拟法隔声量计算结果的影响；通过与有限元（FEM）驻波管模拟法、有限元-统计能量（FEM+SEA，简称FS）混响室模拟法以及瑞利-李兹理论法所得隔声量对比，验证BFS方法的有效性和精度。结果表明，BFS驻波管模拟法能够较为准确地模拟驻波管，得到待测材料的隔声量，相对于有限元（FEM）驻波管模拟法，能够有效解决震荡问题，减小计算量，提升计算速度，可适用于全频段声学材料性能的计算和评估，弥补实验手段耗时费力的缺点，尤其是在新产品的开发阶段具有一定的实际意义。

振动与波；BFS方法；有限元法；驻波管；隔声量

实验测定材料吸声性能主要有驻波管法和混响室法两种手段。驻波管法实验设备简单，测试精度可接受，缺点在于不能完全模拟真实的声学环境[1-2]；混响室法模拟实际受声环境，但实验成本高，难度大[3]。总体来说，实验方法测定材料吸声性能对设备、环境以及人员的要求较高，需要耗费较大的人力物力。为了规避实验手段的缺点，快速、方便、准确地获得待测材料的声学性能参数，近些年利用数值模拟进行材料声学性能评估的技术得到了发展。模拟混响室的数值方法发展得相对比较完善，主要有两种，即统计能量（SEA）混响室数值模拟法以及有限元-统计能量混响室数值模拟法（FEM+ SEA，简称FS混响室模拟法）[4-5]。经实验验证，这两种方法在高频段均能较为准确地拟合实验结果，得到混响声源作用下待测声学材料的隔声量和吸声系数，后者在低频段也能保证一定的精度。而模拟驻波管的数值方法主要运用有限元法，简称FEM驻波管法。现有的基于声学软件Virtual Lab对驻波管法的模拟在高频段存在震荡严重、运算量大、速度慢等问题，推广使用上受到诸多限制；而王英敏基于Ansys平台将声压和力进行转换的驻波管模拟方法存在高频精度差、操作过程复杂、计算效率较低的问题[6]。

为了进一步提升驻波管模拟法的精度，使其能够在全频段得到较为准确的计算结果，本文提出了边界元-有限元-统计能量（BEM+FEM+SEA）混合方法，简称BFS驻波管模拟法。该方法适用于声学材料研究阶段或声学产品开发初期，无需耗费巨大的人力、物力、财力进行实验就可以通过数值模拟的手段得到待测试件的隔声量预测值，有效地降低了研究成本。该方法能够较为准确地拟合FEM驻波管模拟法的计算结果，同时有效改善有限元法曲线震荡的现象，一定程度上克服有限元驻法高频计算模型规模大的问题，有效提升计算速度，在全频段隔声量计算上显示出优势。

1 BFS驻波管模拟法的原理

边界元-有限元-统计能量（BFS）驻波管模拟法的基本原理是，基于驻波管法的实验条件要求确定试件尺寸和边界条件（包括入射波的类型及强度、试件边界约束条件等），建立包含边界元、有限元和统计能量子系统的试件结构与周边流体的混合声学数值模型，通过求解统一的结构与声学耦合方程，计算出全频段材料的隔声量。BFS驻波管模拟法主要包括边界元方程与有限元方程的耦合以及有限元方程与统计能量方程的耦合两个过程。

1.1 边界元方程与有限元方程的耦合

考虑边界元流体作用时，结构振动方程可用下式表示

其中K、C、M分别为结构刚度矩阵、结构阻尼矩阵和结构质量矩阵；u为节点位移向量；fs为外激力向量；fp为流体对结构的作用力，可表示为

其中Csf为耦合系数矩阵；Ns为结构插值形函数矩阵；Nf为流体插值形函数矩阵；n为流固耦合面上单元的法向向量；p为流固耦合面上节点的声压向量；Γi为流固耦合面[7]。

1.2 有限元方程与统计能量方程的耦合

有限元统计能量混合方法将声场分为直接场和混响场，前者定义为入射波产生的声场；后者指经过一次以上反射形成的声场。结构响应q可写为以下形式

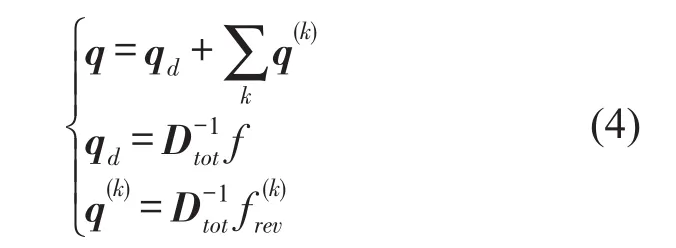
其中Dd是确定性子系统有限元模型的动力刚度矩阵；f是施加在确定性子系统上的外力是子系统k上在混响场所中所受到的力；Dtot是被统计能量子系统直接场的动力刚度矩阵增广后模型的总动力刚度矩阵，是的线性叠加，为有限元和统计能量模型连接处的动力刚度矩阵。子系统j输入到直接场的平均功率为

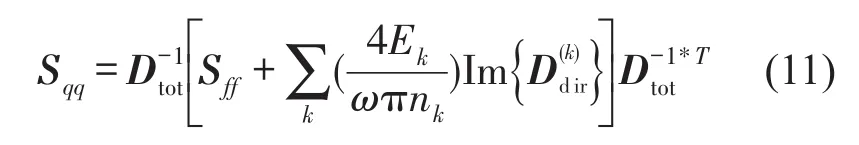
式(10)和式(11)为有限元统计能量理论的主要方程[8]。

1.3 BFS驻波管模拟法的建模原理

还可得到响应q的互谱矩阵

BFS驻波管模拟法的基本建模过程为：首先建立待测材料构件的有限元模型，以模拟构件声学与结构动力学特性；其次，在构件有限元模型入射波侧建立模拟流体介质的边界元模型（空气、海水或者其它流体），与构件有限元模型耦合连接；最后，在有限元模型反射波侧建立统计能量半无限流场子系统，与有限元模型耦合连接。

接下来施加上述模型的边界条件：模拟驻波管测量隔声量实验中的平面波声源，在边界元流体上施加平面波激励，使其垂直入射于构件表面。利用另一侧的半无限流场子系统获得透射声压。

最后，综合求解边界元、有限元和统计能量耦合方程，获得全频段待测材料的隔声量。

具体的建模尺寸、声源以及边界条件的设置说明如下：BFS驻波管模拟法直接设置声源为平面波，且不设管壁，不会激发出高次波，因此声源距离待测平面的距离不会影响计算结果，且因为BFS驻波管模拟法透射端无反射，所以半无限流体距待测试件的距离也不会影响计算结果。一般的，BFS驻波管模拟法选择与实验所用驻波管横截面大小相当的尺寸来建立待测试件的有限元模型，文中推荐待测试件为350 mm×220 mm的矩形有限元结构，入射声源距离待测试件500 mm，另一侧的半无限流场也距待测试件500 mm。同样由于BFS驻波管模拟法消除了高次波和管壁的影响，其工作频率也不再受到驻波管尺寸的限制，所以可以在全频域内求解隔声量。建议在测试频段内均采用声压值为1 Pa（折算为94 dB）的平面入射声波，方向垂直于待测试件平面；待测材料在安装时不应受到不恰当的挤压，BFS驻波管模拟法可以采用的边界条件为无约束边界条件。具体模型如图1所示。

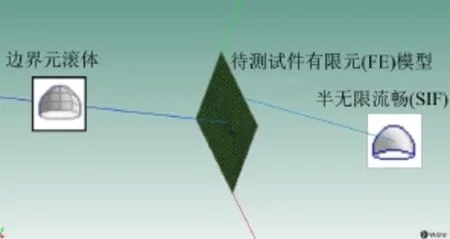
图1 BFS驻波管模拟法示意图

下述的算例分别探讨无约束边界、四边固支边界、四边简支边界、短边简支边界以及长边简支边界五种边界条件下隔声量计算的精度。

2 BFS驻波管模拟法的算例验证

以铝板隔声量计算为例对提出的BFS驻波管模拟法进行精度验证。首先探讨不同的边界条件对BFS驻波管模拟法计算结果的影响，其结果与FEM驻波管模拟法得到的结果进行对比，从而确定BFS驻波管模拟法应当采用的、使隔声量计算结果最为准确的边界条件，其中FEM驻波管模拟法采用Virtual Lab标准算例算法；其次，BFS驻波管模拟法的隔声量计算结果与FS混响室模拟法隔声量计算值和瑞利李兹理论计算值相比较，从而说明不同声源条件对隔声量计算结果的影响，其中瑞利李兹法是混响声源激励下隔声量的理论计算方法，FS混响室模拟法采用的是VA One软件算例。本研究采用目前国际上公认的权威声学分析软件VA One进行数值模拟，其耦合损耗因子由VA One程序内嵌算法确定，程序中参数一般取常规经验值，所得结果满足常规计算精度。

2.1 模型描述

BFS驻波管模型描述如下：测试件为铝板，尺寸为350 mm×220 mm×1 mm，弹性模量G=71.0 GPa，泊松比为0.33，密度为2.81×103kg/m3，损耗因子为0.1%。建立如图1所示的BFS模型，半无限流场子系统（SIF）距铝板有限元模型表面500 mm，流体边界元（BEM Fluid）距铝板有限元模型表面500 mm，入射平面波（plane wave）声压值为1Pa（折算为94 dB），频率区间为16 Hz～8 kHz。

对比模型说明：

(1)FEM驻波管模型：采用Virtual Lab软件计算，铝板的尺寸及材料特性同BFS驻波管模型，定义为结构有限元网格，在发声侧和受声侧建立空气声学有限元网格，将单板模态耦合到空气与单板的接触面上进行计算。单板的两侧500 mm处建立场点，提取场点声压值。在入射声波一侧建立平面波激励，声压值为1 Pa（折算为94 dB），频率区间为16 Hz～8 kHz，FEM驻波管模型如图2所示。

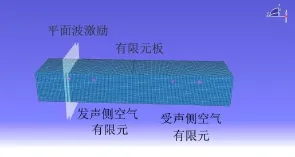
图2 FEM驻波管模拟法示意图

(2)FS混响室模型：FS混响室模拟法可得到混响声源激励下待测材料的隔声量。铝板的尺寸及材料特性同BFS驻波管模型。半无限流场子系统（SIF）距铝板有限元模型表面500 mm，混响声源声压值为1Pa（折算为94 dB），铝板有限元模型的边界条件为简支，频率区间为16 Hz～8 kHz[4]，FS混响室模型如图3所示。

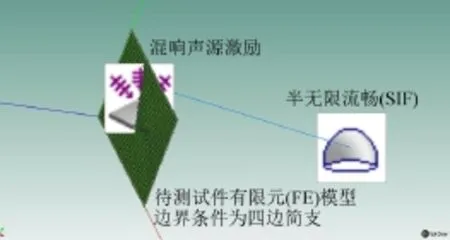
图3 FS混响室模拟法示意图

(3)瑞利李兹法：瑞利李兹法是求取混响声源激励下隔声量的理论解法，文献[8]中给出了详细的计算方法，文中引用其中低频段的数据进行对比。

2. 2 边界条件对隔声量计算的影响

BFS驻波管模型分别采用无约束边界、四边固支边界、四边简支边界、短边简支边界以及长边简支边界，定义为工况一、工况二、工况三、工况四和工况五，分别计算五种工况下单层铝板的隔声量，与FEM驻波管模型、FS混响室模型以及瑞利李兹法计算得到的隔声量进行比较，从而确定BFS驻波管模型的边界条件。采用隔声量TL为指标对结果进行评价，定义

其中LP1为入射声压值，LP2为透射声压值，单位为dB。

本例中入射声压LP1为94 dB(Pa)，由于软件算法的原因，利用VA One软件求取时，不能直接认为受声侧半无限流体的声压值LSIF为透射声压，需要进行修正，因此利用BFS驻波管模拟法计算隔声量时需引入修正量L0，单位为dB。

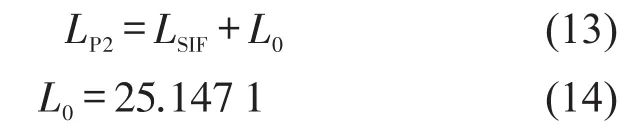
五种工况下单层铝板的隔声量曲线与FEM驻波管模拟法得到的隔声量曲线如图4所示。

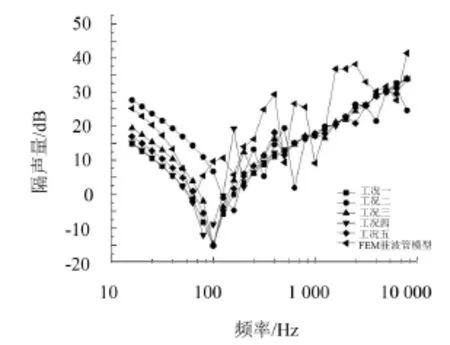
图4 五种工况隔声量计算结果曲线图

从整体看，FEM驻波管模拟法在高频段有明显的震荡现象。而在高频段（110 Hz以上），五种工况的BFS驻波管模型均进入了质量控制区，边界条件对结果影响很小，这也显示了统计能量法的优点，即由于是平均意义上能量分析结果，高频段计算结果准确、震荡小。而在低频段（160 Hz以下），模型处于刚度控制区，不同工况的边界条件对隔声量影响较大，由于共振，不同边界条件的模型在各自固有频率附近隔声量表现出明显的峰谷现象，且边界约束越强，震荡现象越严重。从单个曲线看，FEM驻波管模型结果在高频段不稳定，震荡严重；从平均意义上说，工况一（无约束边界条件）的隔声量曲线在低频段低于FEM驻波管模型结果，高频段较为准确；工况二（固支边界条件）由于边界约束强，总体震荡严重，低频段计算结果偏大；工况三（简支边界条件）隔声量曲线中频段有小幅度震荡，低频段和高频段拟合较好；工况四（短边简支边界条件）和工况五（长边简支边界条件）与FEM驻波管模拟法隔声量对比，存在低频段偏小、中频段震荡的问题。

综合分析来看，工况一（无约束边界条件）的隔声量曲线整体趋势和缓，无明显震荡，较早地进入质量控制区，因此，当重点关注待测材料的全频段的平均吸声性能时，可采用无约束边界条件；工况三（简支边界条件）在全频段拟合最好，低频段的隔声量计算结果最接近FEM驻波管模拟法结果，高频段趋势平缓，因此工况三可用于全频段隔声量的计算。缺点在于，在结构共振频率附近，隔声量曲线会出现明显的峰值现象，在使用时需要进行人为修正。

从图5中可以看出：FS混响室模拟法和瑞利李兹法计算的都是混响声源激励下的隔声量，本质上模拟的是混响室实验方法；而BFS驻波管模拟法和FEM驻波管模拟法计算的是平面声源激励下待测材料的隔声量，本质上是模拟驻波管实验方法。图5显示，两种激励下的隔声量趋势一致，但是混响室模拟法的隔声量会高于驻波管模拟法的隔声量。

图5 BFS、FEM、FS以及瑞利李兹法隔声量计算结果对比

综上所述，BFS驻波管模拟法采取无边界条件时，从平均意义上讲，全频段隔声量计算较为准确，这与王英敏对FEM驻波管模拟法研究的结论一致[6]，即边界条件越弱，对隔声量结果的影响就越小；边界约束越强，隔声量曲线会出现大的波动，需要人为进行修正；BFS驻波管模拟法采取简支边界条件时与FEM驻波管模拟法隔声量拟合最好。因此，BFS驻波管模拟法建议根据所关注的重点不同，对试件采用无约束边界条件或者简支边界条件。

3 结语

为了弥补声学材料实验研究方法要求高、成本大的缺点，结合边界元、有限元以及统计能量法的原理，提出了一种新的驻波管数值模拟方法，即BFS驻波管模拟法，给出该方法的使用条件以及实施该方法的具体试件尺寸、约束边界条件、声源强度等建模细节。对该方法在采用不同边界条件时的隔声量计算结果进行探究，通过与FEM驻波管模拟法结果的对比，验证了该方法的有效性。研究表明：

（1）材料隔声量研究的实验手段需要耗费较大的人力、物力、财力，BFS驻波管模拟法利用数值模拟的方法较为准确地得到待测材料全频段的声学性能，在产品研究和开发初期能够起到有效节约成本、提高效率的作用。

（2）当采用无约束边界条件或简支边界条件时，BFS驻波管数值模拟法的隔声量计算结果在全频段上与FEM驻波管模拟法计算结果相当；利用BFS驻波管数值模拟法计算得到的待测材料的隔声量能够保证一定的精度，可以正确反映材料的声学性能。

（3）BFS驻波管数值模拟法能够有效地模拟驻波管的声学环境，并解决FEM驻波管数值模拟法震荡严重、在高频计算计算量大的问题，简化了操作过程，在全频段隔声材料的性能评估方面显示出优势。

总体来说，BFS驻波管模拟法是对实验方法的有效数值模拟。在实际应用中，可评估和计算待测材料声学性能，作为实验方法的辅助手段运用，还可用于复合材料的开发及声学包的设计等工作。

[1]朱蓓丽，罗晓辉.驻波管中的隔声量测试方法[J].噪声与振动控制，2000，20(6)：41-43.

[2]陶猛，王广玮.驻波管中测量声学材料的隔声量[J].噪声与振动控制，2013，33(5)：210-212.

[3]贺加添.矩形混响室中吸声系数测量结果的检验[J].声学技术，1996，15(1)：6-6.

[4]应申舜，卢奂采，姜伟.多孔橡胶材料声传递损失性能分析：模型描述[J].轻工机械，2013，31(6)：1-4.

[5]毛伟，杨云铠，周书兵.基于LMS Virtual Lab的薄金属铝板的隔声量计算研究[J].重庆建筑，2014，13(10)：16-19.

[6]王英敏，胡碰，朱蓓丽.单层薄板在共振频率区隔声性能的有限元分析[J].噪声与振动控制，2006，26(4)：55-57.

[7]陈磊磊，陈海波，郑昌军，等.基于有限元与宽频快速多极边界元的二维流固耦合声场分析[J].工程力学，2014 (8)：63-69.

[8]COTONI V,SHORTER P,LANGLEY R.Numerical and experimentalvalidation ofa hybrid finite elementstatistical energy analysis method[J].The Journal of the Acoustical Society ofAmerica,2007,122(1):259-270.

BEM/FEM/SEAHybrid Method for Sound Transmission Loss Calculation ofAcoustic Materials

SHI Jia-xin,YANG De-qing,YU Yang
(Collaborative Innovation Center forAdvanced Ship and Deep-Sea Exploration, State Key Laboratory of Ocean Engineering,School of Ship,Ocean and Construction Engineering, Shanghai Jiaotong University,Shanghai 200240,China)

BEM-FEM-SEA hybrid method(BFS method)is proposed to simulate the standing wave tube to get the transmission loss of acoustic materials.The influence of different boundary conditions on the transmission loss is discussed. The effectiveness and accuracy of the BFS method is verified by comparing its isolation result with the results of FEM standing wave tube method,FEM-SEA reverberation simulating method and Rayleigh-Ritz method.The results show that the BFS method can accurately simulate the standing wave tube and obtain the sound insulation of the materials.In comparison with the FEM for simulation of the standing wave tube,this method can be used in the overall frequency domain with better accuracy and lower computation cost.It can make up for the shortcomings of the experimental means.It is of practical significance for research and development of new products.

:vibration and wave;BFS method;FEM method;standing wave tube method;sound transmission loss

O429

：A

：10.3969/j.issn.1006-1335.2016.06.012

1006-1355(2016)06-0062-05

2016-07-07

国家自然科学基金资助项目(51479115)

石嘉欣（1992-），女，陕西省铜川市人，硕士生，主要研究方向为船舶结构减振降噪理论方法。

杨德庆（1968-），男，辽宁省海城市人，教授，博士生导师。E-mail:yangdeq@sjtu.edu.cn