新型恒力末端执行机构力学特性研究
2016-12-27刘海平孙鹏飞史文华王耀兵
刘海平,孙鹏飞,从 强,史文华,王耀兵
(1.北京空间飞行器总体设计部,北京 100094;2.空间智能机器人系统技术与应用北京市重点实验室,北京 100094)
新型恒力末端执行机构力学特性研究
刘海平1,2,孙鹏飞1,2,从 强1,史文华1,王耀兵1,2
(1.北京空间飞行器总体设计部,北京 100094;2.空间智能机器人系统技术与应用北京市重点实验室,北京 100094)
单根纵向受载变形梁与线性螺旋弹簧并联使用,提出一种可实现恒力输出的新型末端执行机构。分别建立了单根受载变形梁和恒力末端执行机构的力学模型。利用解析方法参数化分析了单根受载变形梁设计参数和线性螺旋弹簧预载荷对恒力末端执行机构输出力学特性的影响。考虑恒力末端执行机构在未知环境精细操作过程中冲击载荷的影响,假设受到典型半正弦冲击载荷作用,利用四阶龙格-库塔法对恒力末端执行机构动力学方程进行求解。计算结果表明:单根受载变形梁的纵向预压缩量、自由长度和线性螺旋弹簧预载荷可调整恒力机构的输出力幅值和有效恒力范围;冲击脉冲持续时间长度和系统阻尼可影响恒力末端执行机构输出动态力的幅值和衰减时间。
振动与波;恒力;末端执行机构;受载变形梁;力学特性
随着机器人技术的发展,各领域极端环境工况下机器人被越来越广泛地应用。其中,机器人在复杂未知环境中的精细操作技术始终是重点发展的关键技术之一。目前,针对机器人在未知环境下的精细操作技术的研究大多是通过力控制技术实现[1-2],即在关节或末端执行器上安装力/力矩传感器,实现机器人对操作力的感知,并通过力控制算法进行闭环控制。对机器人采用力控制方法解决精细操作问题可能带来的不足,主要有如下两点:
(1)机器人多为柔性,在其关节上布置力/力矩传感器将进一步降低关节输出轴的扭转刚度和展开基频;然而,力控制方法则希望机器人的结构基频越高越好;
(2)在未知环境下操作,机器人的末端执行机构可能会瞬时突变过载或受到碰撞冲击作用,有可能超出力/力矩传感器的量程,甚至有造成系统破坏的风险。
因此,现有基于力控制的机器人精细操作方式将对系统软硬件、操作安全和可靠性带来一系列问题,有必要研制一种可同时满足精细操作和安全性可靠性要求的恒力末端执行机构。
近年来,在一定输入位移条件下,可提供近似恒力/恒力矩输出的机械式执行机构成为研究热点[3-5]。相关研究主要利用优化设计方法构建由无预载变形薄片梁、连杆和弹簧组合体、柔性铰链等不同方案组成静态载荷作用下可实现恒力输出的机构。对于动态载荷(碰撞冲击,正弦振动)的响应特点研究则较少涉及。
恒力执行机构在恒力输出范围内其动态刚度近似为零,因此又可称为零刚度或者准零刚度机构。根据力学知识,力-位移关系曲线的斜率即为刚度值。基于薄片矩形截面梁在纵向受载达到临界屈曲状态时表现为负刚度输出特征,并联线性正刚度弹簧所构建的准零刚度机构已经被应用于振动防护和能量吸收等领域[6-13]。但是,这些研究工作主要关注在环境扰动影响下,准零刚度机构对输入载荷的振动抑制效果,与恒力末端执行机构的使用环境、安装条件及关注的静动态力学性能指标区别较大。
使用纵向预载变形梁作为负刚度调节元件,与线性螺旋弹簧并联构成恒力末端执行机构,并对其静动态力学特性展开研究。首先,对单根纵向受载梁的力学特性进行数学表征,通过参数化分析对其力-位移特征展开研究;然后,对并联线性螺旋弹簧构成恒力末端执行机构的输出特征展开研究;最后,假设恒力机构受到半正弦冲击载荷作用,对其载荷输出特性进行参数化分析。相关研究成果可为后续恒力末端执行机构的工程应用奠定理论基础。
1 恒力末端执行机构
恒力末端执行机构设计方案的三维模型如图1所示。主要由结构外壳、末端接头、单根梁、预载调整机构和线性螺旋弹簧等组成。
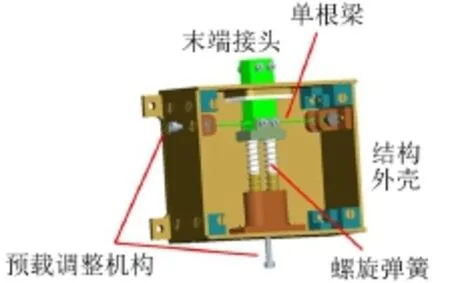
图1 恒力末端执行机构三维模型(未施加预载)
2 单梁模型
单根梁受纵向载荷作用的变形如图2所示。其中,单梁两端固支,其纵向压缩载荷可以由变形势能得出。
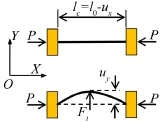
图2 单根梁变形示意图
构建由无预载变形薄片梁、连杆和弹簧组合体、柔性铰链等不同方案组成静态载荷作用下可实现恒力输出的机构。
由图2可见,假设在纵向载荷P作用下,单梁纵向受载变形量为ux。其中,l0为未受载单梁自由长度,lc为纵向受载变形梁的长度。单梁内储存的势能为
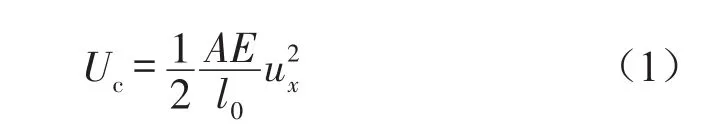
其中A为矩形截面梁的截面面积,E为材料杨氏模量。
两端固支受载变形梁的横向变形满足第1阶模态振型的形函数
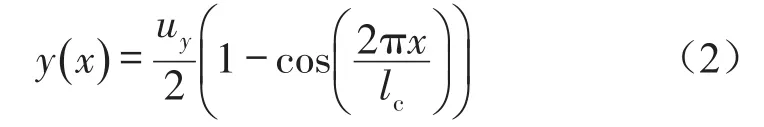
其中uy为单梁中点在横向载荷Ft作用下的位移,x为单梁长轴方向的坐标。
纵向受载变形梁在横向载荷作用下的长度减小量等于受载变形梁的弧长变化量。利用弧长公式,得到
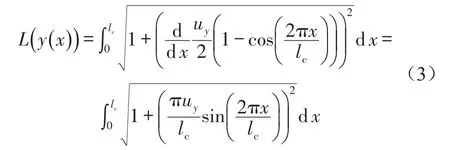
根据参考文献[14]给出的近似计算方法,由弧长公式(3)可化简得到弧长表达式
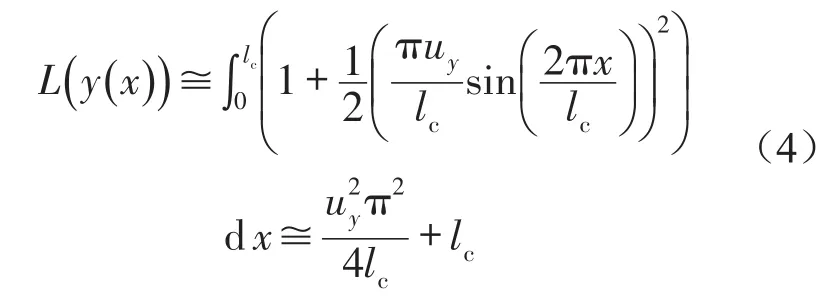
由纵向受载变形梁在横向载荷作用下的弧长公式(4)减去纵向受载变形梁的长度lc,可以得到单梁的长度变形量。结合未受横向载荷Ft作用时纵向受载变形梁的势能公式(1),得到单梁内储存势能的变形梁在变形过程中的势能变化量。
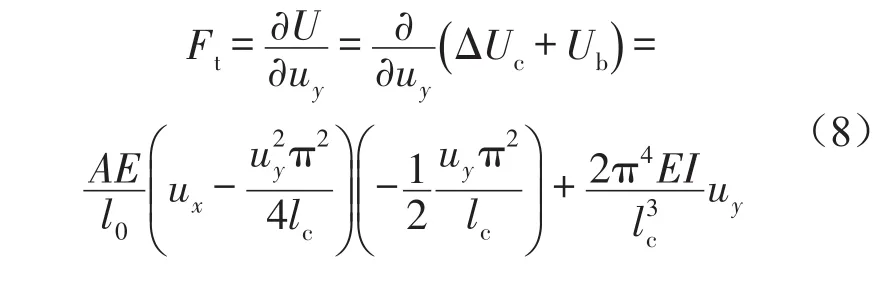
3 恒力机构模型
单根受载变形梁在达到临界屈曲状态时表现出不稳定的负刚度区域,为了实现恒力末端执行机构的恒力输出特性,与线性螺旋弹簧并联,力学模型如图3所示。其中,FL为施加给末端执行机构的外部载荷,Fr为预载调整机构给恒力执行机构施加的预载荷,ks为线性螺旋弹簧刚度,c为阻尼系数,m为末端接头的质量。
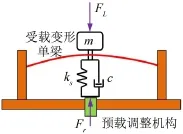
图3 恒力末端执行机构示意图
由图3得到,纵向受载变形梁和线性螺旋弹簧并联后的输出合力为
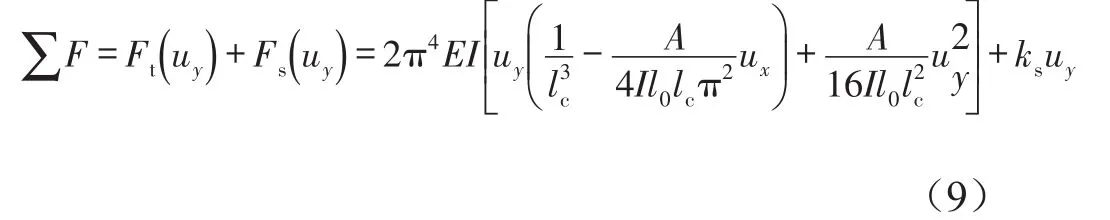
其中Ft为受载变形梁的横向力,Fs为线性螺旋弹簧的回复力。
根据图3所示力学模型,得到系统动力学方程
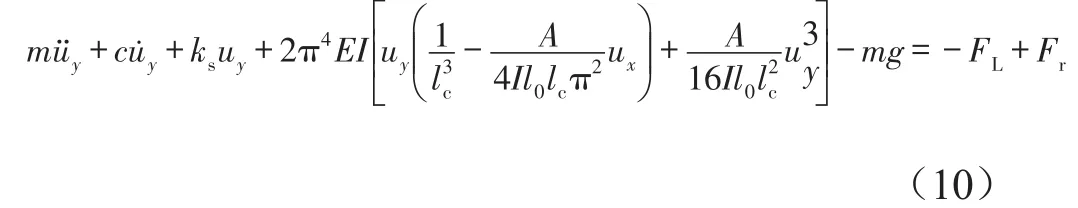
为了便于计算分析,假设y1=uy,y2=y,式(10)可化简为常微分方程组
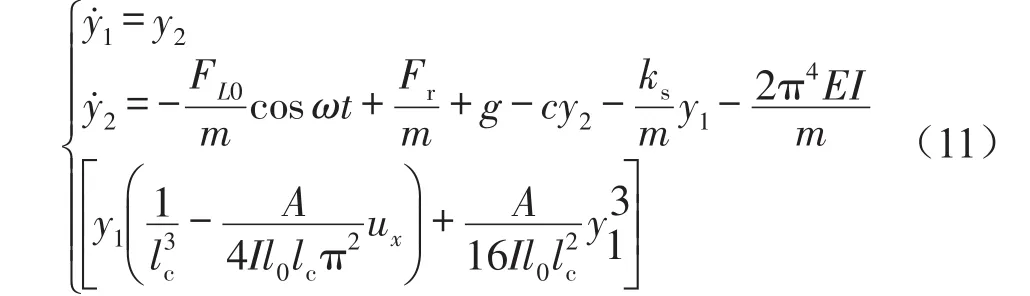
其中FL0为输入力幅值,ω为输入激励圆角频率,t为时间。
4 算例
利用以上所建静动态力学模型,分别采用受载变形梁横向力-位移关系的解析表达式和四阶龙格-库塔法对恒力末端执行机构进行参数化分析研究和力学性能评价。
为了便于后续试验验证,考虑利用树脂材料,采用快速成型技术生产试验件(本文暂不涉及),各设计参数详见表1。
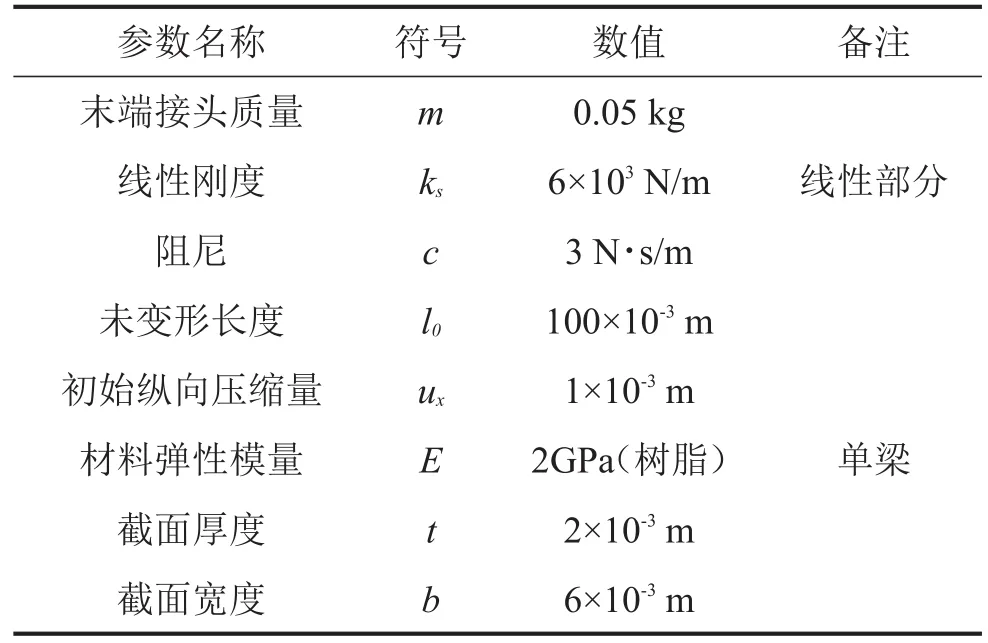
表1 计算参数初值
4.1 单梁静态力学特性
利用所建立单梁静态力-位移关系式(8),计算不同初始纵向压缩量ux=0.1 mm、1 mm、3 mm对应单梁横向力-位移关系,结果如图4所示。
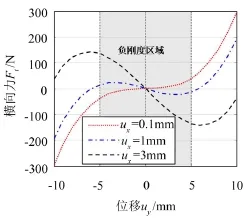
图4 不同初始压缩量条件下单梁横向力-位移曲线
由图4可见,初始压缩量增大,受载变形梁负刚度值增大(即曲线斜率增加);同时负刚度区域增大,参见图中阴影区域。因此,在该阴影区域需要增加一个正刚度元件才可以使输出总刚度为零,即实现恒力输出。
图5给出单梁自由长度变化分别取值l0=60 mm、100 mm、140 mm,对应单梁横向力-位移曲线。可见,随着单梁自由长度增大,单梁负刚度值减小,而负刚度区域增大。
4.2 恒力末端执行机构静态力学特性
将受载变形梁与线性螺旋弹性并联通过刚度调节可实现恒力输出,两部分的合力参见式(9)。将表1中初始设计参数代入式(9),得到恒力末端执行机构的横向力-位移曲线,如图6所示。
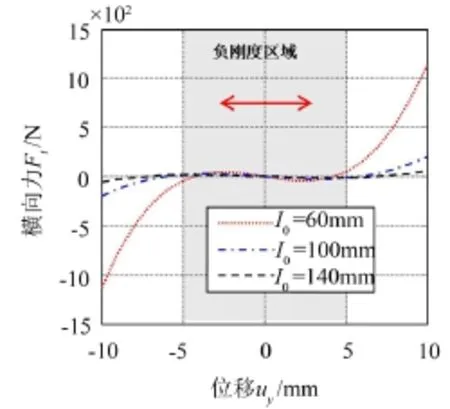
图5 不同自由长度条件下单梁横向力-位移曲线
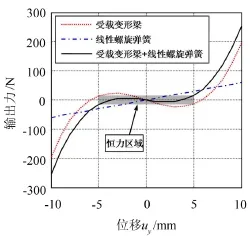
图6 恒力末端执行机构横向力-位移曲线
由图6可见,并联线性螺旋弹簧以后,由于叠加特性使变形梁负刚度区域变为准零刚度区域。其中,输出合力的变化量满足误差要求(一般误差取± 10%)的区域均可认为实现近似恒力输出的设计目标,参见图6中的阴影部分。近似恒力即为输出合力为定值,作为机器人的恒力末端机构可保证受外部载荷作用传递到根部传感器的力为定值。
实际工程中,未知环境产生的载荷是随机变化的。因此,为了提高恒力末端执行机构的承载能力和环境适应性,可对线性螺旋弹簧施加预载荷Fr。
假设对线性螺旋弹簧施加初始预载荷Fr=100 N,恒力末端执行机构的输出力-位移关系如图7所示。由图可见,对线性螺旋弹簧施加预载荷使恒力末端执行机构的恒定输出力区域由Ft=0附近移动到Ft=100 N附近,提高了承载能力。
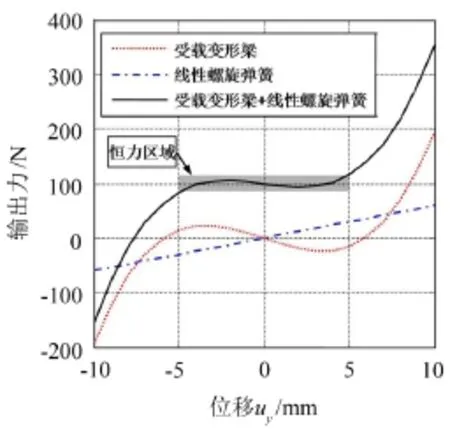
图7 恒力末端执行机构横向力-位移曲线(有预载荷)
4.3 恒力末端执行机构动态力学特性
恒力末端执行机构主要作为机器人的精细操作末端执行单元,在未知环境下操作时在与目标物体接触瞬间将发生碰撞,因此有冲击载荷作用到末端执行机构上。为了评估恒力末端执行机构在瞬时冲击载荷作用下的动态力学特性,假设输入载荷为典型的半正弦冲击波。
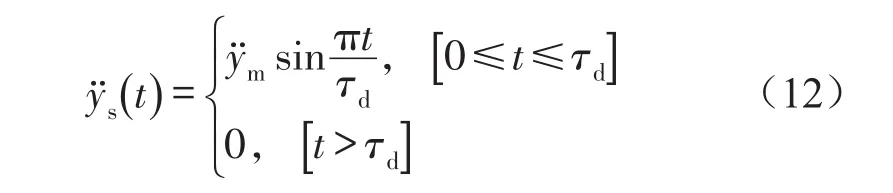
图8给出在冲击载荷作用下,恒力末端执行机构与常规线性螺旋弹簧缓冲效果的比较。其中,任取c=3 Ns/m,Fr=100 N。由图可见,恒力末端执行机构和常规线性弹簧均可对冲击载荷产生缓冲效果,加速度响应峰值衰减量均在50%以上。对比第1个加速度响应峰值,分别为4.7 m/s2和5.1 m/s2;可见,安装恒力末端执行机构可比安装线性弹簧加速度响应峰值减小约8%。
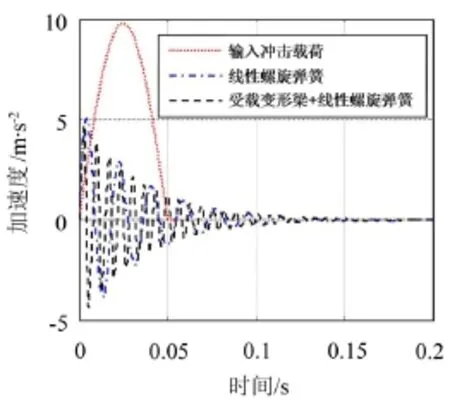
图8 恒力末端执行机构抗冲击效果曲线
图9给出半正弦冲击波作用下,恒力末端执行机构在施加预载荷Fr前后的加速度响应。此时暂不考虑阻尼的影响,即c=0。由图可见,冲击载荷传递到恒力机构后响应幅值显著降低。其中,Fr=0 N时,加速度响应幅值减小约为输入加速度幅值的0.1倍;Fr=100 N时,加速度响应幅值减小约为输入加速度幅值的0.5倍。可见,预载荷施加前后均可以有效抑制冲击载荷的影响。
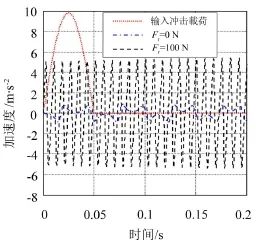
图9 恒力末端执行机构加速度-时间曲线(无阻尼)
考虑系统阻尼(c=3 N·s·m-1)对恒力末端执行机构在冲击载荷作用下动态响应特性的影响,计算结果参见图10。由图可见,受阻尼影响,施加预载荷Fr前后恒力末端执行机构加速度响应幅值衰减时间显著减小,且经过0.15 s以后,冲击载荷引起的加速度响应变为0。
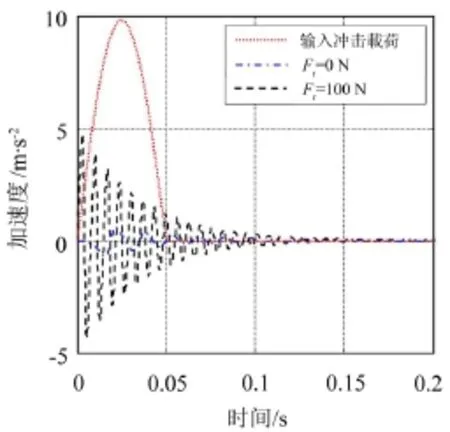
图10 恒力末端执行机构加速度-时间曲线(有阻尼)
图11给出不同冲击时长对恒力末端执行机构加速度响应的影响。图中为了便于对比,计算结果暂不考虑阻尼对系统响应的影响。可见,冲击时长分别取τd=0.001 s、0.05 s、0.5 s时,加速度响应幅值和相邻响应峰值时间间隔均减小。
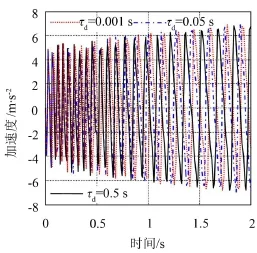
图11 不同冲击时长τd条件下恒力末端执行机构加速度-时间曲线
为了更直观对比在动态冲击载荷作用下恒力末端执行机构的输出力特性,假设初始状态施加预载荷Fr=100 N。利用以上计算得到的位移和加速度响应作为输入,求解得到输出动态力-时间曲线参见图12。由图可见,不考虑系统阻尼的影响,c=0,受冲击载荷作用,恒力末端执行机构输出动态力随时间变化,出现不同峰值的力脉冲响应沿着输出力幅值100 N附近上下振荡,其中最大值约500 N。导致该现象出现的原因在于受载变形梁在负刚度区域内波峰和波谷两个状态发生交替变换,参见图4和文献[10]。考虑系统阻尼的影响,分别取c=3 N·s·m-1和10 N·s·m-1,恒力末端执行机构输出动态力随着时间迅速衰减,趋于预载荷值Fr=100 N;阻尼增大,使输出动态力趋于恒定力的时间更短,并且显著降低了输出力的幅值。
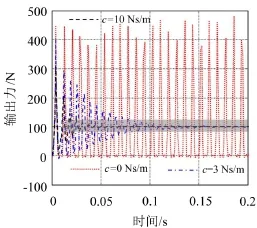
图12 不同阻尼c条件下恒力末端执行机构横向动态力-时间曲线
综上所述,当恒力末端执行机构在未知环境下开展精细操作时,为了防止冲击载荷导致的过载影响,可以通过调整受载变形梁与螺旋弹簧的组合刚度以及阻尼提供缓冲保护。
5 结语
通过纵向受载梁并联线性螺旋弹簧,提出一种可改善现有机器人力控制问题的新型恒力末端执行机构。根据机构的几何构型,分别建立单根受载变形梁和恒力末端执行机构的静动态力学模型。分别采用受载变形梁横向力-位移关系的解析表达式和四阶龙格-库塔法对恒力末端执行机构进行求解,参数化研究恒力末端执行机构在静载和半正弦冲击载荷作用下的力学特性。
根据计算结果,主要得到如下结论:
(1)通过调整纵向受载梁的自由长度和预压缩量,可以调整其输出的负刚度值和负刚度范围;同时发现与线性螺旋弹簧并联后输出的动态力和恒力范围也受其影响;
(2)调整恒力末端执行机构的动态输出力,可通过给线性螺旋弹簧施加预载荷的方式实现;
(3)恒力末端执行机构可以抑制输入冲击载荷引起的加速度峰值;但是,给线性螺旋弹簧施加预载荷将使加速度响应峰值增大。另外,冲击载荷持续时间增加,恒力末端执行机构的加速度响应幅值和相邻响应峰值时间间隔减小;
(4)受冲击载荷影响,恒力末端执行机构的输出动态力随着受载变形梁在负刚度区域内波峰和波谷两个状态之间交替变换,呈现脉冲响应特征;且相比输入冲击载荷,加速度响应得到了显著降低;在此基础上,可以通过调整恒力末端执行机构的系统阻尼进一步降低力脉冲峰值和持续时间长度;随着时间增加,力脉冲趋近于线性螺旋弹簧的预载荷值Fr,即恒力末端执行机构的额定输出力值。
研究成果可为机器人恒力末端执行机构的设计及工程应用提供参考,并指导后续的试验验证工作。
[1]徐文福,周瑞兴,孟得山.空间机器人在轨更换ORU的力/位混合控制方法[J].宇航学报,2013,34(10):1353-1361.
[2]李大明.空间机器人在轨自主装配动力学与控制[D].哈尔滨:哈尔滨工业大学,2012.
[3]YI HO CHEN,CHAO CHIEH LAN.An adjustable constant-force mechanism for adaptive end-effector operations[J].Journal of Mechanical Design,2012,134: 031005-1-031005-9.
[4]DHIRAJ R NAHAR,THOMAS SUGAR.Compliant constant-force mechanism with a variable output for micro/ macro applications[C].Proceedings of the 2003 IEEE International Conference on Robotics&Automation, Taipei,Taiwan,September 14-19,2003:318-323.
[5]VOLKAN PARLAKTAS.Spatial compliant constantforce mechanism[J].Mechanism and Machine Theory, 2013,67:152-165.
[6]刘海平,杨建中,罗文波,等.新型欧拉屈曲梁非线性动力吸振器的实现及抑振特性研究[J].振动与冲击,2016,35(11):155-160.
[7]刘兴天,黄修长,张志谊,等.激励幅值及载荷对准零刚度隔振器特性的研究[J].机械工程学报,2013,49(6):89-94.
[8]JINQIU,JEFFERYHLANG,ALEXANDERH SLOCUM.A curved-beam bistable mechanism[J].Journal of Microelectromechanical Systems,2004,13 (2):137-145.
[9]GREGORY L HOIST,GREGORY H TEICHERT,BRIAN D JENSEN.Modeling and experiments of buckling modes and deflection of fixed-guided beams in compliant mechanisms[J].Journal of Mechanical Design,2011, 133:051002-1-051002-10.
[10]BENJAMIN A FULCHER,DAVIDWSHAHAN, MICHAELR HABERMAN,et.al.Analyticaland experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems[J].Journal of Vibration and Acoustics,2014, 136:031009-1-031009-12.
[11]MUSTAFA YALCIN,BIRCAN UZUNOGLU,ELIF ALTINTEPE,et.al.VNSA:variable negative stiffness actuation based on nonlinear deflection characteristics of buckling beams[C]. 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS), Tokyo,Japan,November 3-7,2013.
[12]殷小涛,孟再强,刘兴星,等.非规则弹性片高静低动的隔振特性[J].噪声与振动控制,2013,33(6):45-48.
[13]胡光军,周生通,李鸿光.一种非线性隔振器的静力分析与实验研究[J].噪声与振动控制,2011,31(6):69-71.
[14]VANGBO M.An analytical analysis of a compressed bistable buckled beam[J].Sens.Actuators A,1998,69(3): 212-216.
Study on the Mechanical Characteristics of a Novel Constant-force End Effector
LIU Hai-ping1,2,SUN Peng-fei1,2,CONG Qiang1, SHI Wen-hua1,WANG Yao-bing1,2
(1.Beijing Institute of Spacecraft System Engineering,Beijing 100094,China; 2.Beijing Key Laboratory of Intelligent Space Robotic Systems Technology andApplications, Beijing 100094,China)
Using parallel connection of an axially compressed beam and a linear spring,a novel constant-force end effector is presented.First of all,a transverse force-displacement relationship for the axially compressed beam is derived. Then,a combined dynamic model including the axially compressed beam,the linear spring and a damper,is built.Finally, based on the dynamic model,the influence of some key design parameters on the performance of the constant-force end effector is studied.It is assumed that the constant-force end effector is excited by a typical semi-sinusoidal impact load when it operating in an unknown environment.Then the dynamic equations of the constant-force end effector are solved by using fourth-order Runge-Kutta method.The numerical results exhibit that the value of the output amplitude and the available range of the constant force can be adjusted by changing the values of the axial compression load and the free length of the beam.In addition,the compressive force for the linear spring also can exert some effect on the dynamic performance of the constant-force end effector.The duration of impact pulse and the system damping can also influence the amplitude of the dynamic output force and the attenuation time for the responses of the constant-force end effector.
vibration and wave;constant force;end effector;axially compressed beam;mechanical characteristics
TH113.1;O328;V231.92
:A
:10.3969/j.issn.1006-1335.2016.06.006
1006-1355(2016)06-0026-06
2016-05-31
国家自然科学基金资助项目(51405014);总体设计部青年创新发展基金
刘海平(1982-),男,山西省吕梁市人,博士,高级工程师,主要研究方向为机械结构振动噪声控制。E-mail:lhpvibration@163.com
