基于SPH的水体交互三维虚拟仿真

方贵盛，郑高安

(浙江水利水电学院 机械与汽车工程学院，浙江 杭州 310018)

基于SPH的水体交互三维虚拟仿真

方贵盛，郑高安

(浙江水利水电学院 机械与汽车工程学院，浙江 杭州 310018)

水体与复杂边界物体相互作用时的运动情况非常复杂.目前用基于网格的方法很难准确有效地实现三维模拟.采用基于无网格的光滑粒子动力学方法，通过求解纳维—斯托克斯方程，在VC++和OpenGL编程环境下，实时动态模拟了水体相互碰撞、水流通过圆形桥墩、水流通过丁坝时的三维动作效果.通过与实际水流模拟实验观察效果相比较，验证了所实现算法的有效性，说明SPH方法可广泛应用于水体复杂运动过程模拟，并可用于解决工程实际问题.

纳维—斯托克斯方程；光滑粒子动力学；水体；虚拟仿真

水作为自然界中一种常见的物质，对其研究和仿真具有重要的理论意义和实用价值.由于水在形态上是不规则的，同时也是动态变化的，因此水体的建模与仿真一直是计算机图形学中的一个研究难点，同时也是真实感图形学领域的一个研究热点[1-2].

水体虚拟仿真建模方法包括了基于几何曲面的方法[3]、基于波形函数的方法[4]、基于海浪谱的方法[5]、基于粒子系统的方法[6]、基于物理模型的方法[7-9]等.近年来，随着计算机软硬件技术的发展，基于流体动力学的方法被广泛应用于流体的仿真，取得了良好的效果.本文采用了光滑粒子动力学方法，通过求解纳维—斯托克斯方程，在VC++和OpenGL编程环境下，动态模拟了水体相互碰撞、水流通过圆形桥墩、水流通过丁坝时的动作效果.

1 基于SPH的水流虚拟仿真基本原理

1.1 水流控制方程

描述水流运动的控制方程有圣维南方程、二维浅水动力方程、欧拉方程、纳维—斯托克斯方程等.为了更好地模拟水流的运行，本文采用了纳维—斯托克斯方程组(Navier-Stokes Equations，简称NSE)，它由一系列的偏微分方程来表示，包含了质量守恒方程和动量守恒方程.

质量守恒方程：

▽·U=0

(1)

动量守恒方程：

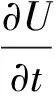
(2)

式中：U—速度矢量；▽—向量梯度算子；

▽2—拉普拉斯算子；t—时间变量；

p—流体的压强；ρ—流体密度；

μ—流体动力粘滞系数；f—单位质量力.

1.2 SPH离散化求解方法

光滑粒子动力学方法(Smoothed Particle Hydrodynamics，简称SPH)是近二十多年来逐步发展起来的一种无网格方法.SPH的基本思想是将连续的流体用相互作用的粒子组来描述，每个粒子点上携带独立的物理信息，包括质量、速度、密度等.通过求解粒子组的动力学方程和跟踪每个粒子的运动轨迹，便可求得整个流体系统的力学行为.采用SPH方法求解NSE方程的关键是采用两次逼近：一是核函数逼近，即将描述场的函数近似表示为该函数和核函数的乘积的积分表示；二是粒子逼近，即将场函数的积分表示用一系列粒子离散化来描述，从而降低了NSE方程求解的难度.根据上述思想，水流粒子的物理量，如密度、压力和速度等，其SPH求解公式分别表示如下：

(3)

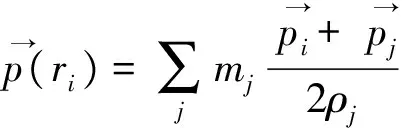
(4)

(5)

式中：mi，mj—粒子i，j的质量；

pi，pj—粒子i，j所受的压力；

ρi，ρj—粒子i，j的密度；

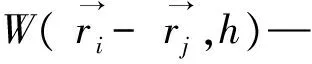
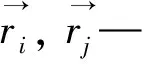
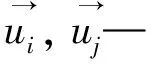
h—光滑核半径.

2 基于SPH的水流虚拟仿真算法实现

2.1 算法的数据结构设计

通过构造粒子类和粒子系统类来确定算法的数据结构.单个粒子的属性包括了粒子的位置、速度、预估速度、颜色、所受的压力、密度、力(加速度)等参数.粒子系统的属性，包括了容纳粒子系统的水箱容器大小、水体的大小、光滑核长度、时间步长、粒子的质量、粘度、静态密度、粒子半径、粒子间距、光滑核半径、内部硬度、外部硬度、阻尼系数等参数.

2.2 算法流程设计

采用SPH方法对NSE进行求解，以模拟水体动态流动过程，其总体设计思路(见图1).

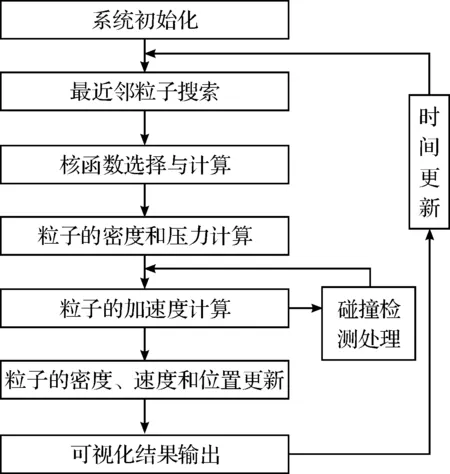
图1 算法的总体设计思路

2.2.1 系统初始化

系统初始化过程需要构造水体仿真场景，设置初始参数，包括水容器的参数、初始水体的参数、基本粒子参数、SPH参数，以及水粒子在容器中的排列方式等.为了提高粒子的最近邻粒子的搜索速度，本文用了空间网格结构，网格初始化构建算法步骤如下.

步骤1：设置网格单元的大小(初始值为核半径的两倍)；

步骤2：确定网格的分辨率，即确定水箱容器X、Y、Z轴各排列有多少个网格单元；

步骤3：计算水容器总共包含有多少个网格单元.

步骤4：为每个网格单元分配指针；

步骤5：设置每个网格单元内粒子的数目，初始值为0.

步骤6：绘制空间网格.

网格构建完成以后，需要将一个个粒子加入到对应的网格中，然后求出每个粒子所在网格的单元索引号，其实现算法如下所示：

步骤1：依次取出一个个水粒子i；

步骤2：确定粒子i的位置，并与空间网格的最小值进行比较，以确定粒子i所在的网格单元索引号；

步骤3：将粒子i插入到对应的网格单元中；

步骤4：粒子i所在的网格单元索引中粒子数加1.

2.2.2 最近邻粒子搜索

常用的最近邻粒子搜索方法有直接粒子搜索技术、关联链表搜索技术、树形结构搜索技术等.本文采用空间网格结构和链表结构来提高最近邻粒子的搜索速度，其算法流程如下所示.

步骤1：取出粒子i，确定粒子i的位置；

步骤2：确定水容器X、Y、Z轴各排列有多少个网格单元；

步骤3：计算最小网格单元的位置；

步骤4：计算粒子i所在的网格单元索引号；

步骤5：按X、Y、Z轴正方向依次计算其余七个邻居粒子网格单元索引号.

2.2.3 核函数选择与计算

在SPH计算过程中，核函数的选择至关重要，它不仅决定了函数近似式的形式，而且还决定核近似和粒子近似的一致性和精度.核函数一般应包括归一性、紧支性、对称性、非负性等.常用的核函数有高斯型核函数、B样条核函数、四次样条核函数等，本文选用了Matthias Muller所采用的三种光滑核函数，分别用来求解粒子的密度、压力和粘滞力等[10].

2.2.4 粒子的密度和所受的压力计算

本文利用空间网格结构来计算粒子所受的压强力，其算法流程如下所示：

步骤1：依次取出一个个水粒子i，采用最近邻粒子搜索方法，查找它的邻居粒子所在的八个网格单元号；

步骤2：从邻居网格单元中取出一个个粒子j，如果取出的粒子是i粒子，则取下一个粒子，否则计算粒子i与j之间的距离；

步骤3：如果粒子i与j之间的距离小于光滑核半径，则计算式子(6)的值；

(6)

步骤4：判断粒子i的邻居粒子数是否小于40，如果满足条件，则创建邻居对列表，并计算邻居粒子对的间距；

步骤5：根据公式(7)计算粒子i的密度；

(7)

步骤6：根据公式(8)计算粒子i所受的压强力，式中K为常数，ρ0为初始密度；

pi=K(ρi-ρ0)

(8)

步骤7：根据压强力的大小设置粒子的颜色值.

2.2.5 粒子所受的合力和加速度计算

本文采用空间网格结构和邻居列表结构计算粒子的加速度，其算法流程如下所示：

步骤1：依次取出一个个水粒子i；

步骤2：从水粒子i的邻居列表对中依次取出水粒子i的一个个邻居粒子j；

步骤3：计算水粒子i与邻居粒子j间的距离；

步骤4：根据公式(9)计算粒子i由于所受的压力差而引起的加速度；

(9)

步骤5：根据公式(10)计算粒子i由于所受的粘滞力而引起的加速度.

(10)

2.2.6 碰撞检测处理，粒子的加速度更新

在边界处，粒子除了受到重力外，还受到固壁边界的作用，此时粒子将改变原有的运动方向、速度和加速度.为了防止粒子穿越固壁边界，本文采用了Matthias Muller所介绍的施加边界力的方法[10].如果粒子与边界间的距离小于2r(r为粒子的半径)，则更新粒子的运动方向和加速度.

2.2.7 粒子的密度、速度和位置更新

SPH的时间积分方法，广泛采用蛙跳法、预测校正法、龙格库塔法等，均具有二阶时间精度.由于在实际运用过程中，蛙跳法对存储的需求量低，而且计算效率高，因此本文选用蛙跳积分方法来计算粒子演进的速度和位置.

2.2.8 可视化结果输出

在每个计算步结束后，可以得到每个粒子的密度、加速度、速度、位置和所受的压力等参数.根据这些数据，用户可以观察到任何时刻的粒子位置分布、速度分布和压力分布等，可以输出不同时刻的速度、压力等值线图，也可以直观地看到水体的产生、演进和变形的全过程，这对于评价或修改工程设计方案有很大帮助.

3 水体仿真实例

仿真实验在Windows 7平台上进行，采用VC++.net和OpenGL编程工具分别实现了两侧水体的相互碰撞效果仿真、水流通过丁坝时的动态效果仿真、水流通过圆形桥墩时的动态效果仿真等.实验的硬件环境为Intel酷睿八核处理器，CPU 2.4 GHz，4 G内存，1 G独立显存.

3.1 水体碰撞效果仿真

水箱容器长0.56 m，宽0.16 m，高0.32 m；左侧水体长0.12 m，宽0.16 m，高0.045 m，粒子数为3 059个；右侧水体长0.12 m，宽0.16 m，高0.097 m，粒子数为6 555个.粒子初始间距为0.006 m，按长方体规律分布，动力粘滞系数为0.2 kg/(m·s)，计算时间步长为0.004 s.初始时刻，两侧水体在重力作用下沿着壁面边界流动(见图2).

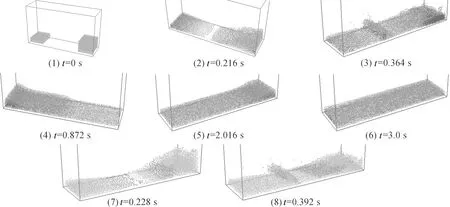
图2 水体碰撞仿真效果

从图2可以看出，初始时刻，两侧水体在重力的作用下流动，由于受水箱侧壁的影响，左侧水体向右流动，右侧水体向左流动.由于右侧水体比左侧水体大，右侧水体的流动速度比左侧水体快，经过了0.232 s后两侧水体相互碰撞，压力增大.左侧水体受右侧水体的冲击，水体流动方向发生改变，向上跃起并折回，同时溅起水花.接着两侧水体融合在一起，继续向左侧流动，当碰到左侧壁时，左侧的水体升高，右侧降低，然后又在重力和惯性力的作用下，向右侧流动，当碰到右侧壁时，又向左侧移动，如此反复，经过5 s后水体趋向平衡静止.图2(7)、(8)中反映了两侧水体的流动速度状况.刚开始时，水平流动速度较小，然后逐渐增大，当两侧水体发生碰撞时，又有一个速度变小的过程，与实际观察的结果相吻合.

3.2 水流通过丁坝时的动态效果仿真

水箱容器长0.8 m，宽0.16 m，高0.32 m；梯形丁坝的上底为0.04 m，下底为0.08 m，高度为0.024 m，长度为0.08 m，丁坝最左侧位置与水箱左侧壁间的距离为0.4 m；水体长0.16 m，宽0.16 m，高0.1 m，粒子数为9 928个(见图3).粒子初始间距为0.006 m，按长方体规律分布，动力粘滞系数为0.2 kg/(m·s)，计算时间步长为0.004 s.

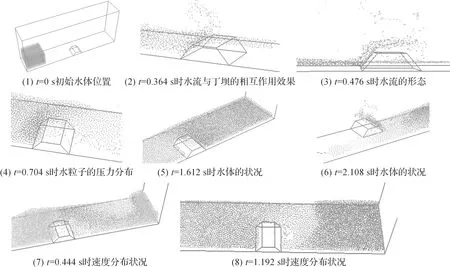
图3 水流通过丁坝时的动态效果仿真

初始时刻，水体在重力作用下沿着壁面边界流动.当水流到达梯形丁坝时，由于受到丁坝坡面的影响，一部分水体沿着坡面向上运动并越过丁坝，一部分水体受丁坝的阻挡被折回，还有一部分水体绕过丁坝向前推进.当水流到达水箱右侧壁时，在壁面的影响下，水体被折回，然后向左流动，并再次通过丁坝.由于水流通过丁坝时，速度不一致，在右侧壁的影响下，将会产生涡流效果.图3(1)～(6)反映的是水流通过梯形丁坝时的位置及压力分布效果，图3(7—8)为水流速度分布状况，青色为低速部分粒子，黄色为高速部分粒子.

3.3 水流通过圆形桥墩时的动态效果仿真

水箱容器长0.8 m，宽0.16 m，高0.32 m；桥墩半径为0.032 m，高度为0.32 m，桥墩轴心与水箱左侧壁间的距离为0.48 m；水体长0.16 m，宽0.16 m，高0.1 m，粒子数为9 936个(见图4).粒子初始间距为0.006 m，按长方体规律分布，动力粘滞系数为0.2 kg/m·s，计算时间步长为0.004 s.

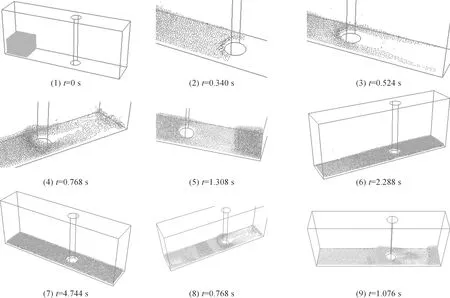
图4 水流通过圆形桥墩时的动态效果仿真

初始时刻，水体在重力作用下沿着壁面边界流动，速度逐渐增大.当水流到达圆形桥墩时，由于受到桥墩的阻力，靠近桥墩表面水粒子压力增大，速度减慢，水位升高.桥墩两侧的水粒子兵分两路绕过桥墩向前推进，速度增大，当达到水箱右侧壁时，由于受到阻力的影响，水流向后折回，同时溅起水花.当5 s后，水位趋于平稳.图4(1)～(7)反映的是水流通过圆形桥墩时的位置及压力效果，图4(8)、(9)为水流速度分布效果，青色为低速部分粒子，黄色为高速部分粒子.

4 结 论

基于无网格的SPH水体运动仿真算法，能够解决基于网格的水体模拟方法中存在的单元划分、网格缠结和扭曲等问题，在模拟水体大变形及波浪破碎等方面具有独特的优势，因此得到广泛的应用.本文采用基于光滑粒子动力学方法，通过求解纳维—斯托克斯方程，在VC++和OpenGL编程环境下，实时动态地模拟了水体相互碰撞、水流通过圆形桥墩、水流通过丁坝时的三维动作效果，模拟结果比较理想，与实验效果吻合较好.对于更复杂的水体交互问题，有待于进一步研究.

[1] 方贵盛,潘志庚.水体虚拟仿真与应用综述[J].计算机仿真，2012，29(10):30-33,361.

[2] 方贵盛，潘志庚.水体虚拟仿真建模技术研究进展[J].系统仿真学报，2013，26(9):1981-1989.

[3] JAY Allen FAULKNER. Beauty Waves: an Artistic Representation of Ocean Waves Using Bezier Curves [D]. Texas: Texas A & M University,2006.

[4] 赵 欣，李凤霞，战守义.基于小振幅波理论的浅海波浪建模及动态仿真[J].系统仿真学报,2008,20(2):281-284.

[5] 杨怀平，孙家广.基于海浪谱的波浪模拟[J].系统仿真学报，2002，14(9):1175-1178.

[6] 张尚弘，陈 垒，赵登峰.基于粒子系统的流场实时模拟[J].水利水电技术，2004，35(9):47-50.

[7] TSUNEMI TAKAHASHI,HIROKO FUJII,ATSUSHI KUNIMATSU. Realistic Animation of Fluid with Splash and Foam [J]. Computer Graphics,2002,21(3):736-744.

[8] MARKUS IHMSEN,NADIRAKINCI,MARC GISSLER. Boundary Handling and Adaptive Time-Stepping for PCISPH[C]]// Kenny Erleben. Proceedings of the 7thWorkshop on Virtual Reality Interaction and Physical Simulation,Aire-la-Ville: The Eurographics Association,2010:79-88.

[9] NADIR AKINCI,MARKUS IHMSEN,GIZEM AKINCI. Versatile Rigid-Fluid Coupling for Incompressible SPH [J],Acm Tranctions on Graph,2012,31(4):1-62.

[10] MATTHIAS MULLER,DAVID CHARYPAR,MARKUS GROSS. Particle-based Fluid Simulation for Interactive Applications[C]]//D. Breen. Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer animation,Aire-la-Ville: The Eurographics Association,2003:154-159.

3DVirtualSimulationofWaterInteractionBasedonSPH

FANG Gui-sheng,ZHENG Gao-an

(College of Mechanical and Automotive Engineering,Zhejiang University of Water Resources and Electric Power,Hangzhou 310018,China)

When water interacts with complex boundary objects,the movement is very complicated. It is difficult to realize 3D simulation of this phenomenon by using the grid-based method. In this paper,a real-time virtual simulation method based on SPH is proposed. In the programming environment of VC++ and OpenGL,the Navier-Stokes equation is solved to simulate some complex water phenomena,such as interaction between water and water,interaction between water and pier,and interaction between water and spur dike. Experimental results show that the method is realistic and can be used to solve some project problems.

Navier-Stokes Equations; smoothed particle hydrodynamics; water; virtual simulation

2016-03-18

2013年度浙江省水利厅科研基金资助项目(RC1337)

方贵盛(1973-)，男，江西婺源人，博士，教授，主要研究方向为人机交互与虚拟仿真技术.

TP391.9

A

1008-536X(2016)10-0068-06