连续油管带筛管双重管柱岩屑运移模型研究

杨睿月, 黄中伟, 李根生, 沈忠厚, 韩 树, 许争鸣

(中国石油大学油气资源与探测国家重点实验室,北京 102249)



连续油管带筛管双重管柱岩屑运移模型研究

杨睿月, 黄中伟, 李根生, 沈忠厚, 韩 树, 许争鸣

(中国石油大学油气资源与探测国家重点实验室,北京 102249)

连续油管带筛管喷射侧钻多分支井钻完井一体化是一种新型的多分支井钻井方法,针对本技术连续油管和筛管所形成的双重管柱,开展岩屑运移试验研究,采用Monte Carlo方法预测岩屑颗粒进入割缝筛管与连续油管之间环空的情况,并计算环空中被岩屑颗粒堵塞的临界参数。结果表明:双重管柱岩屑运移存在悬浮层、跃移层、静止岩屑层以及筛管与连续油管之间的砂堵层。由于具有更小的环空过流面积,双重管柱的岩屑运移能力比常规连续油管钻井高。试验条件下,砂堵层不发生堵塞的临界条件是:当缝宽介于岩屑颗粒之间时,泵排量高于0.98 L/s,或机械钻速小于40.09 km/h,缝宽比岩屑粒径越大,临界机械钻速越小;当缝宽大于岩屑颗粒直径时,泵排量高于0.88 L/s或机械钻速小于5.74 km/h。

多分支井; 连续油管; 割缝筛管; 岩屑运移; 蒙特卡洛方法

连续油管带筛管喷射侧钻多分支井钻完井一体化是一种新型的多分支井钻井方法,可实现一趟管柱同时完成连续油管喷射钻井和割缝筛管完井[1]。国内外学者已对常规连续油管钻水平井岩屑运移模型进行了大量研究[2-8]。该技术在钻进过程中是连续油管外套筛管的双重管柱,而目前对于岩屑运移的研究是针对环空中存在单一管柱,双重环空携岩问题尚未见到相关的报道和研究。笔者采用室内试验与数值模拟的方法相结合,研究连续油管带筛管双重管柱条件下的岩屑运移模型,并预测岩屑颗粒进入割缝筛管与连续油管之间环空的出砂情况。

1 试验装置及方法

1.1 试验设备

连续油管带筛管喷射侧钻多分支井钻完井一体化技术在钻进过程中是连续油管外套筛管的双重管柱(图1),二者前端由分离装置相连,后端由橡胶圈密封。根据该技术的特点,设计了以下试验装置与方法。

图1 连续油管带筛管双重管柱

试验装置包括高压柱塞泵、多功能携岩试验架、水箱、岩屑添加装置、固液分离器、模拟井筒(有机玻璃管)、连续油管、割缝筛管、石英砂、高速摄影机等。

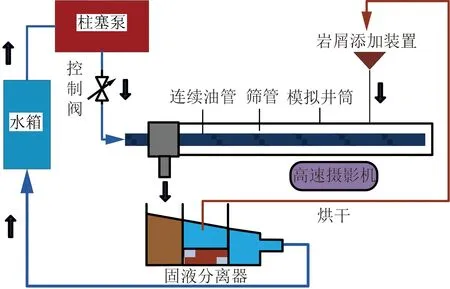
图2 试验设备示意图

1.2 试验材料

试验管柱参数见表1。

表1 管柱参数

割缝筛管缝长80 mm,缝密度150条/m,1#筛管缝宽0.5 mm,2#筛管缝宽0.6 mm。

利用目数筛得到的岩屑颗粒粒径分布:2.36～4.75、2.00～2.36、0.85～2.00、0.43～0.85、0.18～0.43 mm,岩屑密度为2.85 g/cm3。

1.3 试验方案

1.3.1 试验测量值

试验一,测量不同粒径岩屑颗粒的临界滚动速度、临界悬浮速度和临界运移速度,其中临界运移速度是指岩屑全部处于悬浮态或形成的岩屑床可以整体随着冲砂液移动,而没有静止的岩屑床形成[10]。

试验二,测量不同排量下单层连续油管和双重管柱的岩屑床湿周,对比两种管柱的岩屑运移效率并拟合岩屑床湿周与排量的关系。

1.3.2 试验步骤

试验一,临界速度测量:

(1)连接管线,安装各接头,调试各仪器,开泵循环直至井筒内水流稳定,无气泡。以稳定的速度向井筒内注入岩屑,模拟钻井过程中岩屑的产生。

(2)在井眼中铺好岩屑床后,关闭柱塞泵使岩屑均匀地停止在井眼底部,将流体排出,停止泵入钻井液和岩屑。

(3)开泵。逐渐增加泵的排量,直到岩屑床最上层的岩屑开始逐层滚动运移,记录下此时的流量Q1,则临界滚动速度为vr=Q1/Af,其中Af为井筒与筛管之间的环空截面积。

(4)待临界滚动速度测定完毕,重新开泵,调整泵排量,在岩屑床开始滚动后继续增大泵排量,直到岩屑颗粒离开岩屑床进入悬浮运移状态,记录下此时的流量Q2,则临界悬浮速度为vs=Q2/Af。

(5)待临界悬浮速度测定完毕,重新开泵,调整泵排量,在岩屑颗粒离开岩屑床进入悬浮运移状态后继续增大泵排量,直到所有颗粒悬浮在环空中而没有静止岩屑床形成,记录下此时的流量Q3,则临界运移速度为vm=Q3/Af。

试验二,岩屑床湿周测量:

(1)连接管线,安装各接头,调试各仪器,井筒内放入连续油管,不加筛管。

(2)启动柱塞泵,调整泵排量,循环直至井筒内水流稳定,无气泡。

(3)以稳定的速度向井筒内注入岩屑,并开始计时。岩屑进入井筒中,逐渐形成岩屑床,待岩屑床高度稳定时,在井筒段3个不同的测点分别测量岩屑床湿周的长度并记录数据。

(4)待3 min加砂完毕后,停泵,接收携带出井筒内的岩屑,烘干后称量并记录质量m1。

(5)待悬浮颗粒完全沉降,开泵,将井筒中所有的岩屑携带至固液分离器的纱网中,烘干后称量并记录质量m2。

(6)依次增大泵排量,重复以上步骤。

测试完单层连续油管之后,按相同的步骤测量不同排量下连续油管带筛管时岩屑床的湿周。

1.3.3 试验测算物理量

(1)无因次岩屑床湿周。无因次岩屑床湿周是指静止岩屑床在环空周向上的长度与井筒内壁周长的比值，

(1)

式中,S为无因次岩屑床湿周;Lc为静止岩屑床在环空周向上的长度,mm;dw为井筒内径,mm。

(2)机械钻速。试验中的机械钻速通过控制单位时间内的加砂质量模拟实际钻进过程中产生的岩屑,机械钻速为

(2)

式中,vROP为试验中模拟的机械钻速,m/h;Ms为规定时间内加砂总质量,kg;t为加砂时间,h;AWSL为井筒与筛管之间的环空截面积，m2;ρs为砂粒密度,kg/m3。

2 试验结果讨论

2.1 双重管柱岩屑运移模型

常规连续油管钻进时,随着泵排量的变化,连续油管与井眼的环空内会形成悬浮层、跃移层和静止岩屑床(图3(a))。连续油管带筛管钻井中,岩屑颗粒会从割缝中进入到筛管与连续油管之间的密闭环空,大部分岩屑颗粒一旦进入将很难运移出，因此悬浮层、跃移层、静止岩屑床在筛管与井筒的环空之间形成,岩屑颗粒堆积在筛管与连续油管的环空之间,定义为砂堵层(图3(b)),形成了双重管柱岩屑运移四层模型。砂堵层中岩屑颗粒与管壁的摩擦增大了连续油管与筛管分离时的阻力,可能导致连续油管卡在井筒之中,尤其是环空被砂粒堵塞时,连续油管与筛管分离的难度增加,因此有必要对岩屑颗粒进入筛管与连续油管之间的环空情况进行研究。

图3 双重管柱岩屑运移四层模型

将连续油管与筛管分离后(图4)，可以清晰地看到连续油管壁上有一层砂,这一层砂是在岩屑运移过程中细粒岩屑通过割缝缝隙进入,因此割缝参数的选择不仅要考虑地层出砂的粒径,还要考虑射流钻头喷射钻进过程中钻出的岩屑颗粒的粒径。如果钻煤层,由于煤粉颗粒较小,可以考虑将割缝筛管换成绕丝筛管。

图4 试验观察到的砂堵层出砂

2.2 岩屑运移临界速度

试验得到的岩屑运移临界速度见表2。由试验观察可知,岩屑颗粒的运动速度小于临界滚动速度时,井筒与筛管的环空之间几乎充满岩屑颗粒,筛管被岩屑全部覆盖。当岩屑颗粒的运动速度大于临界悬浮速度时,井筒与筛管的环空之间有稳定岩屑床形成,部分筛管被岩屑床覆盖。当岩屑颗粒的运动速度大于临界运移速度时,岩屑颗粒全部处于悬浮状态,没有岩屑床形成,筛管没有被岩屑颗粒覆盖。

表2 试验测量岩屑运移临界速度

2.3 岩屑运移排量与岩屑床湿周

排量与双重管柱无因次岩屑床湿周的关系如图5所示。图5中随着排量的增加,无因次岩屑床湿周总体呈下降趋势。这是由于排量的增加提高了环空返速,使冲砂液的紊流强度增加,缓解了岩屑的堆积效应,岩屑颗粒易离开静止的岩屑床向前移动或进入高速悬浮区。此外,双重管柱的岩屑床湿周始终小于单根连续油管,前者比后者小4.25%～11.15%。这是由于双重管柱减小了环空过流面积,增加了环空局部流速。排量从0.68 L/s提高到0.93 L/s,连续油管的岩屑床湿周降低了23%,而双重管柱降低了34%。筛管的加入有利于提高岩屑的运移能力,且提高排量对井眼净化效率的提高更加有效。

图5 双重管柱无因次岩屑床湿周与排量的关系

拟合无因次岩屑床湿周与泵排量之间的关系,环空中只有单根连续油管时:

SCT=1.14-0.65Q,R2=0.98.

(3)

式中,SCT为环空中只有单根连续油管时的无因次岩屑床湿周;Q为排量,L/s。

环空中是双重管柱、割缝宽度为0.6 mm时二者函数关系为

SSLSCT=1.25-0.88Q,R2=0.92.

(4)

式中,SSLSCT为环空中为双重管柱时井筒与筛管之间环空的无因次岩屑床湿周。

环空中是双重管柱、割缝宽度为0.5 mm时二者函数关系为

SSLSCT=1.19-0.75Q，R2=0.97.

(5)

3 Monte Carlo 数值模拟

3.1 数值模型的建立

采用Monte Carlo(MC)算法对砂堵层内的出砂情况进行预测[10],主要考虑颗粒的粒径与缝宽之间的关系,判定颗粒是否会通过缝隙进入到砂堵层:颗粒直径小于缝宽会进入砂堵层,否则不会进入。由Champura等[11]的研究可知,当一条缝被粒径大于缝宽的砂覆盖了一层之后,筛管出砂量占总出砂量的99.4%,为了减少计算量,假设筛管被第一层大粒径砂覆盖之后筛管就不再出砂,而不考虑从覆盖砂之间的孔隙部分进入的细小砂粒。

初始岩屑颗粒的数量取决于机械钻速即加砂速度,单位时间内产生岩屑的数量为初始颗粒的数量。岩屑颗粒是否进入割缝还与排量有关,可分为以下3种情况:①低排量时,岩屑颗粒运动速度小于临界滚动速度,岩屑床不断升高,最终将整个筛管埋没(图6(a)),此时整个筛管的割缝都会有砂粒进入;②升高排量,直到岩屑颗粒运动速度达到临界悬浮速度,处于悬浮态的岩屑颗粒随着冲砂液向前移动,不会进入割缝中,此时被稳定岩屑床覆盖的割缝部分会有砂粒进入,随着排量的升高,岩屑床高度降低,进入砂堵层的颗粒减少(图6(b));③继续升高排量,岩屑速度达到临界运移速度时,砂粒全部处于悬浮态或没有稳定岩屑床形成,砂粒不会进入割缝中,可能有少部分砂粒由于颗粒之间的碰撞进入割缝,数量极少,不会对砂堵层造成堵塞(图6(c))。用MC进行模拟计算出砂之前还须根据流量判定筛管有多少缝隙可能会进入砂粒。

图6 不同临界流速下岩屑颗粒进入砂堵层情况

MC数值模型假设:①不考虑砂桥的形成对砂粒的阻挡,只根据缝宽阻挡砂粒;②砂粒是规则圆形的;③岩屑床整个筛管与井筒的环空部分,不考虑由于筛管管体的弯曲变形导致的岩屑床高低不平;④井筒内无空气泡存在;⑤通过所有缝隙的流量相同;⑥不考虑颗粒与颗粒之间的碰撞。

MC计算方法:①通过筛分法或激光分选法得到一定质量砂粒的颗粒分布;②在总砂粒中随机选取一颗砂粒,不放回抽样;③如果选取的砂砾直径小于割缝缝宽,则该砂进入砂堵区;如果选取的砂粒直径大于割缝缝宽,则该砂停留在割缝外部;④循环选取砂粒,直到整个缝长上的割缝被滞留在缝隙外部的砂覆盖,程序终止选取砂粒;⑤记录进入割缝的砂粒总数量、总体积及质量比,一条缝出砂计算完毕,循环到步骤②,直到所有的缝计算完毕或者所有的原始砂粒都筛选完毕。

以上步骤为一次MC模拟,循环计算以上步骤10～1 000次,求取平均值即为最终结果。算法流程见图7。

图7 一次MC模拟算法流程

3.2 数值模型验证

MC数值模型对砂堵层出砂预测的准确度通过试验结果进行验证。岩屑运移试验的测试条件:机械钻速17 m/h,加砂总质量4.84 kg,加砂时间3 min,颗粒粒径0.43～0.85 mm,缝宽0.6 mm,缝密150条/m,缝长80 mm,缝单元中的缝数1条,3次测试排量依次为0.4 、0.78 和1.0 L/s。3种排量下分别对应于不同的岩屑运移状态,每组测试共对比了3种砂粒分布(PSD)的出砂情况(图8、表3)。

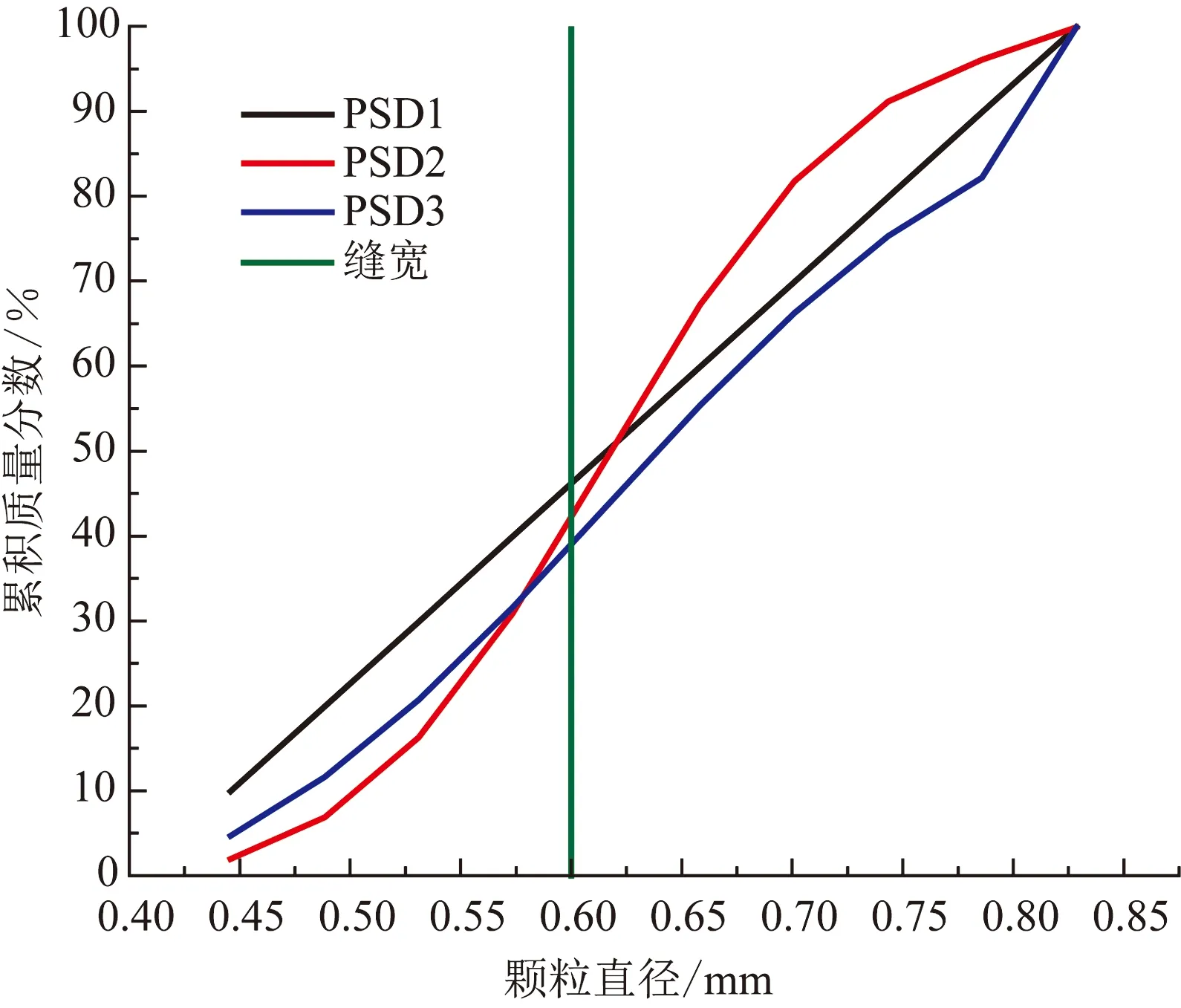
图8 不同颗粒粒径的分布

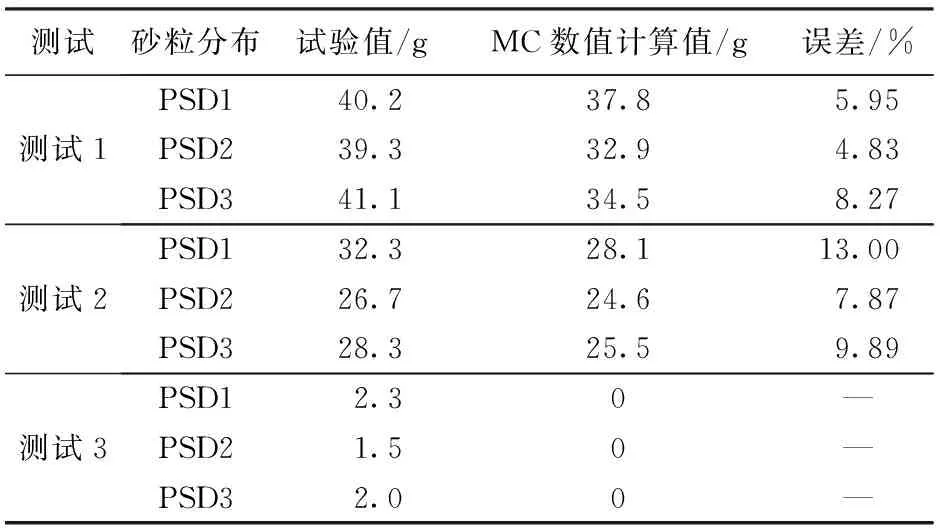
表3 MC模型预测出砂结果与试验对比

由表3可知,当颗粒速度小于临界滚动速度时,试验值与计算值的误差保持在8%以下,介于临界悬浮和运移速度之间时,试验值与计算值的误差保持在13%以下,大于运移速度,绝对误差在2.3 g以下。MC数值模型可以用来预测砂堵层的出砂情况。此外,试验值均大于模型计算值,这是由于模型值中第一层砂将割缝覆盖之后,砂粒就不再进入割缝中,而实际情况会有少部分细小颗粒通过第一层砂粒之间的间隙进入到砂堵层。颗粒介于临界悬浮和运移速度之间的预测误差比第一种情况大,是因为处于悬浮层的颗粒可能由于颗粒之间的互相碰撞作用部分进入到砂堵层。

3.3 砂堵层出砂影响因素

3.3.1 MC模型模拟次数

采用PSD2的砂粒分布、测试1的计算条件,计算不同的MC模拟次数对砂堵层出砂预测的影响。

根据Monte Carlo算法的特点,随机抽样次数越多计算结果越准确[12],因此模拟次数越多,越与真实结果接近。由图9可知,随着模拟次数的增加,尤其是当模拟次数达到100时,结果趋于相等。后续计算中MC模拟次数设定为100次。

图9 MC模拟次数对计算结果的影响

3.3.2 缝 宽

采用PSD2的砂粒分布、测试1的计算条件,计算不同缝宽影响下砂堵层中的出砂情况,结果如图10所示。

图10 缝宽对进入砂堵层砂粒的影响

由图10可知,随着缝宽的增加,进入砂堵层的砂粒显著增多,尤其是在缝宽大于0.7 mm之后,砂粒显著增多,不利于岩屑的清除。由之前的研究[13]可知,缝宽对割缝筛管的抗挤强度和引入的表皮因子影响较小,因此建议采用小缝宽的割缝筛管,如本文中研究的地层砂颗粒粒径为0.43～0.85 mm时,建议采用0.5和0.6 mm的缝宽,即接近于地层砂粒径的平均值。

3.3.3 缝 长

采用PSD2的砂粒分布、测试1的计算条件,计算不同缝长影响下砂堵层中的出砂情况,结果如图11所示。由图11可知,随着缝长的增加,进入砂堵层的砂粒基本呈线性增加,这是由于缝长越长,割缝的流通面积越大,砂粒进入割缝的数量越多。缝长主要控制了颗粒是否继续从样本里随机抽取,缝长越大抽取的次数越多,进入割缝的颗粒越多。

图11 缝长对进入砂堵层砂粒的影响

3.3.4 缝 密

采用PSD2的砂粒分布、测试1的计算条件,计算不同缝密影响下砂堵层中的出砂情况,结果如图12所示。由图12可知,随着缝密的增加,进入砂堵层的砂粒基本呈线性增加,这是由于缝密越多,割缝的流通面积越大,砂粒进入割缝的数量越多。

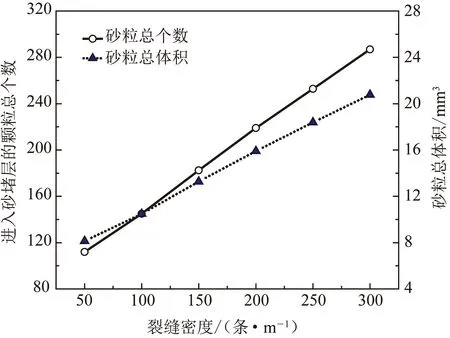
图12 缝密对进入砂堵层砂粒的影响

3.3.5 排 量

采用PSD2的砂粒分布、测试2的计算条件,计算不同的排量影响下砂堵层中的出砂情况,结果如图13所示。由图13中可知,随着排量的增加,进入砂堵层中的砂粒减少,这是因为排量的增加使更多的岩屑颗粒进入悬浮层,降低了岩屑床高度,岩屑颗粒进入割缝的数量减少。排量从0.6 L/s增加到0.93 L/s,进入砂堵层的砂粒总体积减小了32.20%,达到颗粒临界悬浮速度之前和之后砂粒进入砂堵层的量显著下降,提高排量到临界悬浮速度以上是降低砂堵的有效方法。

图13 排量对进入砂堵层砂粒的影响

3.3.6 机械钻速

采用PSD2的砂粒分布、测试1的计算条件,计算不同钻速下砂堵层中的出砂情况,结果如图14所示。由图14可知,随着机械钻速的增加,进入砂堵层中的砂粒增加。机械钻速从1.14 m/h增加到28.40 m/h,进入砂堵层的砂粒总体积增加了3.77%。相比于泵排量的影响,机械钻速的影响较小。

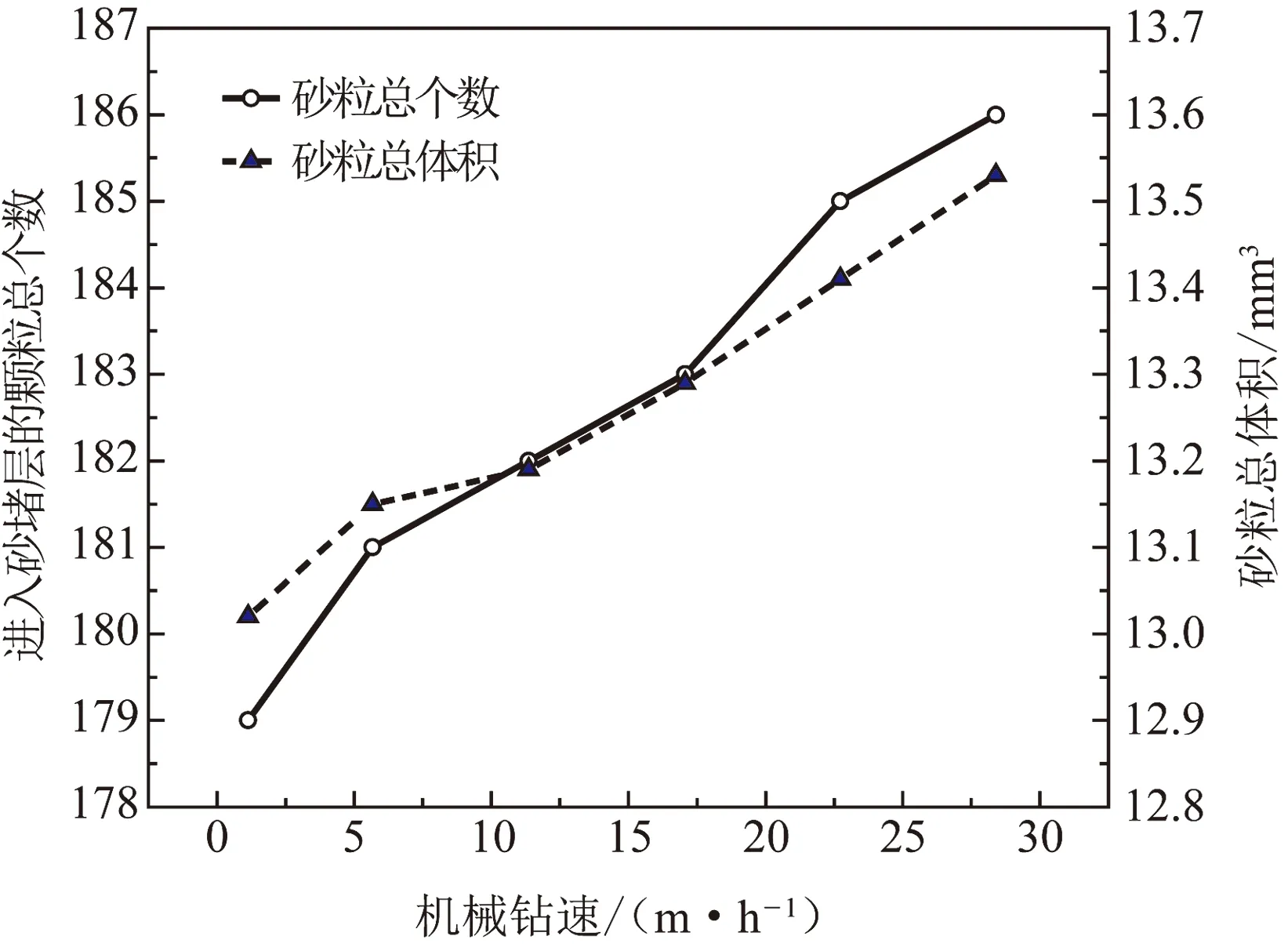
图14 机械钻速对进入砂堵层砂粒的影响

3.4 砂堵层堵塞环空临界参数预测

砂堵层堵塞即筛管与连续油管之间的环空充满砂粒,连续油管不易从筛管中抽出。由MC数值模型的防砂条件,当砂粒的粒径小于缝宽时,砂粒会进入到砂堵层,当粒径大于缝宽时,砂粒不会进入砂堵层。根据砂粒粒径与缝宽的关系可分为以下3种情况:①岩屑粒径大于缝宽时,岩屑不会进入到砂堵层,不存在砂堵层堵塞的情况;②岩屑粒径部分大于缝宽,部分小于缝宽,部分岩屑颗粒会进入到砂堵层,可能引起砂堵层堵塞;③岩屑粒径小于缝宽,岩屑颗粒会全部进入砂堵层,若不控制钻井条件,极易引起砂堵层堵塞。冲砂液排量和机械钻速是控制岩屑颗粒是否会引起砂堵层堵塞的关键参数。

3.4.1 缝宽介于岩屑颗粒直径之间

岩屑粒径部分大于缝宽,部分小于缝宽时,部分岩屑颗粒会进入到砂堵层,可能引起砂堵层堵塞。若排量足够大,颗粒运移速度大于临界运移速度,没有静止岩屑床形成,则砂堵层不会发生堵塞;若小于临界运移速度,只要机械钻速足够小,也不会发生堵塞。以有效清理岩屑为原则钻进,临界运移速度所对应的泵排量为砂堵层不发生堵塞的临界泵排量。临界机械钻速须根据试验结果和MC预测模型进行计算。

由上述讨论可知,岩屑颗粒是否进入割缝缝隙与排量和粒径有关,如果排量和粒径确定,则单位时间内进入缝隙的岩屑体积占总岩屑体积的比值一定,该比值η可通过试验中的加砂质量Ms和MC模型预测Vsb计算得出,其比值为

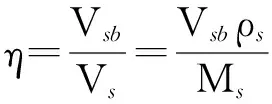
(6)

式中,Vsb为进入缝隙即砂堵层的岩屑体积,m3;Vs为岩屑总体积,m3。

当计算砂堵层堵塞的临界条件时,假设砂堵层全部被砂粒堵塞,即进入到割缝中的砂粒充满了整个连续油管与筛管之间环空的体积,

Vsb=VSLCT.

(7)

其中

VSLCT=ASLCTL.

式中,VSLCT为进入连续油管与筛管之间环空的砂粒的体积m3;ASLCT为连续油管与筛管之间的环空截面积,m2;L为筛管长度,m。

根据式(6)、(7)可计算出当砂堵层堵塞时须加入的岩屑总体积Vs。再根据式(2)可计算出砂堵层堵塞的临界机械钻速,

采用PSD2的砂粒分布、测试1的计算条件,则Ms=4.84 kg,t=3 min,Vsb由MC模型根据不同的缝宽值计算得出。预测结果见表4,只要达到其中一个条件就不会有砂堵现象发生。

表4 0.43～0.85 mm砂粒砂堵层不发生堵塞的临界条件

3.4.2 缝宽大于岩屑颗粒直径

按照MC模型防砂原则,若砂粒运移的临界速度小于其临界悬浮速度，且机械钻速足够大,则所有的砂都会进入到砂堵层,引起砂堵层的堵塞。尤其是喷射钻进煤层时,由于煤粉颗粒较小,沁水盆地开发现场产出的煤粉颗粒粒径为0.008 5～0.085 cm[14],更易引起砂堵,须采用高排量低钻速前进,但是由于煤层易坍塌,提高排量会提高喷射压力,容易造成钻进前方煤层破碎而堵塞井眼,无法继续前进,此时控制钻速更加有效。采用本试验数据,岩屑颗粒为0.18～0.43 mm,缝宽为0.5 mm,预测砂堵层全部堵塞的临界机械钻速为5.74 km/h,临界泵排量为0.88 L/s。只要达到上述其中一个条件就不会有砂堵现象发生。

4 结 论

(1)细砂从割缝的缝隙进入连续油管与筛管之间的密闭环空,形成砂堵层,建立了双重管柱岩屑运移四层模型:筛管与井筒的环空中存在悬浮层、跃移层和静止岩屑床,筛管与连续油管之间的环空存在砂堵层。

(2)双重管柱相较连续油管由于拥有更小的环空过流面积,相同排量下拥有更高的环空返速,提升了环空流体的紊流程度和岩屑颗粒之间的碰撞作用。筛管的加入有利于岩屑的运移。

(3)Monte Carlo 算法通过重复随机抽样,可以较准确地模拟预测砂堵层出砂情况,试验结果与数值模型的平均误差在13%以内。

(4)试验条件下,砂堵层不发生堵塞的临界条件是当缝宽介于岩屑颗粒之间时,泵排量高于0.98 L/s或机械钻速小于40.09 km/h,缝宽越大相应的临界机械钻速越小;当缝宽大于岩屑颗粒直径时,泵排量高于0.88 L/s或机械钻速小于5.74 km/h。

(5)为防止筛管与连续油管之间的环空砂堵,采用该装置进行多分支井钻进时,建议砂岩中主要采用提高排量的方式即大于岩屑颗粒临界运移速度进行钻进，煤层中主要采用低钻速的方式进行钻进。

[1] YANG R, HUANG Z, LI G, et al. Slotted liner sheathing coiled tubing—a new concept for multilateral jetting in coalbed methane wells and laboratory tests of tubular friction performance[J]. Journal of Natural Gas Science and Engineering, 2015,9(26):1332-1343.

[2] GAVIGNET A A, SOBEY I J. A model for the transport of cuttings in highly deviated wells[R]. New Orleans, LA, USA,1986.

[3] DORON P, GRANICA D, BARNEA D. Slurry flow in horizontal pipes—experimental and modeling[J]. International Journal of Multiphase Flow, 1987,13(4):535-547.

[4] DORON P, BARNEA D. A three-layer model for solid-liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow, 1993,19(6):1029-1043.

[5] CHO H, SHAH S N, OSISANYA S O. A three-layer modeling for cuttings transport with coiled tubing horizontal drilling[R]. SPE 63269, 2000.

[6] 郭晓乐,汪志明,龙芝辉.大位移钻井全井段岩屑动态运移规律[J].中国石油大学学报(自然科学版),2011,35(1):72-76. GUO Xiaole, WANG Zhiming, LONG Zhihui. Transient cuttings transport laws through all sections of extended reach well[J]. Journal of China University of Petroleum(Edition of Natural Science), 2011,35(1):72-76.

[7] 马东军,李根生,郭瑞昌,等.管内转向径向水平井携岩规律数值模拟[J].石油机械,2013,41(11):6-10. MA Dongjun, LI Gensheng, GUO Ruichang, et al. Numerical simulation of the cuttings-carrying law in radial horizontal well[J]. China Petroleum Machinery, 2013,41(11):6-10.

[8] 宋先知,李根生,王梦抒,等.连续油管钻水平井岩屑运移规律数值模拟[J].石油钻探技术,2014,42(2):28-32. SONG Xianzhi, LI Gensheng, WANG Mengshu, et al. Numerical simulation on cuttings carrying regularity for horizontal wells drilled with coiled tubing[J]. Petroleum Drilling Techniques, 2014,42(2):28-32.

[9] 宋洵成,管志川,陈绍维.斜井岩屑运移临界环空流速力学模型[J]. 中国石油大学学报(自然科学版), 2009,33(1):53-56,63. SONG Xuncheng, GUAN Zhichuan, CHEN Shaowei. Mechanics model of critical annular velocity for cuttings transportation in deviated well[J]. Journal of China University of Petroleum (Edition of Natural Science), 2009,33(1):53-56,63.

[10] PEDEN J M, FORD J T, OYENEYIN M B. Comprehensive experimental investigation of drilled cuttings transport in inclined wells including the effects of rotation and eccentricity[R]. SPE 20925, 1990.

[11] CHANPURA R A, FIDAN S, MONDAL S, et al. New analytical and statistical approach for estimating and analyzing sand production through wire-wrap screens during a sand-retention test[J]. SPE Drilling & Completion, 2012,27(3):416-426.

[12] 谢中华.MATLAB统计分析与应用:40个案例分析[M].北京:北京航空航天大学出版社,2010:1689-1819.

[13] 杨睿月,黄中伟,李根生,等.煤层气水平井割缝筛管优化设计[J].煤炭学报,2014,39(11):2269-2275. YANG Ruiyue, HUANG Zhongwei, LI Gensheng, et al. Optimization design for the geometry parameters of slotted liner in coal bed methane horizontal wells[J]. Journal of China Coal Society, 2014,39(11):2269-2275.

[14] 韩国庆,高飞,竺彪,等.煤层气井煤粉颗粒表观机械运移规律[J].煤炭学报,2013,38(增2):364-369. HAN Guoqing, GAO Fei, ZHU Biao, et al. Superficial transport mechanisms of coal particles in the coal-bed methane well[J]. Journal of China Coal Society, 2013,38(sup2):364-369.

(编辑 李志芬)

Slotted liner sheathing coiled tubing—a dual-pipe model for cuttings transport

YANG Ruiyue, HUANG Zhongwei, LI Gensheng, SHEN Zhonghou, HAN Shu, XU Zhengming

(StateKeyLaboratoryofPetroleumResourcesandProspectinginChinaUniversityofPetroleum,Beijing102249,China)

Drilling with slotted liner sheathing coiled tubing (SLSCT) is a new technique for multilateral jetting, which is designed to synchronize the jet drilling and liner tube running in one trip. Its drilling assembly includes dual-pipes, thus the cuttings transport efficiency in a dual-pipe mode needs special analysis. In this study, laboratory experiments were conducted to investigate the cuttings transport mechanisms in a dual-pipe system. A Monte Carlo algorithm was proposed to determine the amounts of cuttings entering the annulus between the coiled tubing and slotted liner, and it was also used to estimate the critical pumping rate and drilling rate for the case of cutting blocking. A four-layer model for cuttings transport with the SLSCT multilateral jetting was established, including suspension layer, moving bed layer, stationary layer and cutting blocking layer, which exist in the annulus between the coiled tubing and slotted liner. The cuttings carrying capability of a dual-pipe system is higher than that of the conventional coiled tubing drilling due to the smaller flow area thus the higher annular pumping velocity. Under the experiment conditions of this research, the critical condition for no cutting blocking is that, in the case the slot size smaller than the cutting particle size, the pumping rate is higher than 0.98 L/s, or the ROP is smaller than 40.09 km/h, and the wider the slot size, the lower the ROP. In the case of the slot size larger than the cutting particle size, the pumping rate is recommended to be higher than 0.88 L/s, or the ROP is smaller than 5.74 km/h.

multilateral well; coiled tubing; slotted liner; cuttings transport; Monte Carlo method

2015-12-24

国家科技重大专项(2011ZX05037-001)

杨睿月(1989-),女,博士研究生,研究方向为煤层气连续油管喷射钻完井技术。E-mail:ruiyue_yang@126.com。

黄中伟(1972-),男,教授,博士,博士生导师,研究方向为油气钻完井和压裂增产。E-mail:huangzw@cup.edu.cn。

1673-5005(2016)05-0087-09

10.3969/j.issn.1673-5005.2016.05.010

TE 21

:A

杨睿月,黄中伟,李根生,等.连续油管带筛管双重管柱岩屑运移模型研究[J]. 中国石油大学学报(自然科学版),2016,40(5):87-95.

YANG Ruiyue, HUANG Zhongwei, LI Gensheng, et al. Slotted liner sheathing coiled tubing—a dual-pipe model for cuttings transport[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(5):87-95.