通胀市场下多设备租赁的在线策略分析

徐维军，刘幼珠，陈晓丽，胡茂林，高 丽

(1. 华南理工大学工商管理学院，广东 广州 510641；2. 淮阴师范学院数学科学学院，江苏 淮安 223300；3. 华南理工大学数学学院，广东 广州 510641)



通胀市场下多设备租赁的在线策略分析

徐维军1，刘幼珠1，陈晓丽1，胡茂林2，高 丽3

(1. 华南理工大学工商管理学院，广东 广州 510641；2. 淮阴师范学院数学科学学院，江苏 淮安 223300；3. 华南理工大学数学学院，广东 广州 510641)

现实租赁市场中，企业同时租赁多台设备的现象大量存在，但经营者面临的最大难题是如何对这多台设备进行在线租赁的组合优化，从而降低决策成本，而通货膨胀又进一步增加了决策难度。本文运用在线算法和竞争分析法建立多设备投资的风险控制策略，并分析通胀对决策的影响。首先在Karp经典模型上给出通胀因素下多设备投资的最优在线和离线策略；接着建立设备租赁在连续可分情形下的最优风险控制模型，进一步结合实际投资中设备必须以离散整数租赁的特点，对CR策略进行调整和优化，得到近似的CRJ策略，使得策略更符合实际投资活动。最后给出具体实例分析，结果显示，当物价指数逐渐增大时，最优决策日期相应提前，对应最优策略的竞争比也逐渐增大，进一步说明物价指数因素和多设备投资因素的引入对投资者的决策有着重要的影响，为多设备在线租赁问题的研究提供了新的解决思路。

通货膨胀；多设备租赁；在线算法；竞争分析

1 引言

日常经济活动中，设备不断多样化呈现且设备更新速度不断加快已成为事实，随着经济的发展、市场竞争的越来越激烈，为追求资金的利用效率，越来越多企业一改传统投资思维模式，即由原来偏好固定资产投资倾向于根据市场的需求情况灵活地租赁多台设备，如航空公司租赁飞机、医院租赁大型医疗设备等。我国的租赁行业也由此快速增长，机构数量从2009年的160多家增加到现在的约750家，业务总量从2009年的3000亿元增长到现在的19000亿元，租赁逐渐成为经济活动中一种常见的投资方式。而当真正做决策时，不得不考虑市场中其它宏观因素的影响，如，通货膨胀因素。2000年末我国的广义货币M2仅为13.8万亿元，2015年1月已达124.3万亿元，14年间净增长110.5万亿元，涨8倍多；同期，2000年末人均GDP为9.9万亿元， 2014年末达到63.64万亿元，净增长54万亿元，涨5倍多；对比货币供应量和GDP的增长情况发现，货币发行增长率远大于经济增长率，导致货币贬值、物价急剧攀升。由于通货膨胀因素的影响，企业生产过程中的设备资产等价格不断上涨，这对投资者的投资决策产生重要影响。因此，基于现实背景和投资决策需要，研究通货膨胀中的设备投资租赁问题具有一定的现实意义。

虽然许多学者对该问题进行了大量研究，但是他们大多从税收对租赁决策的影响[1]、租赁对企业财务结构的影响[2]及租赁对企业绩效的影响[3]等角度进行研究。然而在实际的设备投资活动中，由于种种因素限制，投资者往往无法精确知道设备使用的时间段，但又不得不立即做出采用何种投资策略的决定，此时如何进行设备的投资使得成本最低呢？1992年，Karp[4]首先运用在线算法和竞争分析法对该问题进行了研究，他假设，设备的购买价格是p，每期租金是1，经过分析和证明给出最优的在线策略是：在前p-1期内采用一直租赁设备的策略，而一旦第p期仍需要则购买(该策略的竞争比达到最小为2-1/p)。在Karp提出的经典“租雪橇”模型基础上，众多国内外学者进行深入的扩展研究。Yaniv[5]在此基础上提出市场利率下的确定性在线租赁模型，并扩展给出均衡策略下的随机性在线策略。进一步，Binali[6]考虑投资者的风险偏好，给出风险补偿下的在线租赁策略。之后，学者们在此基础上继续考虑投资活动中伴随的市场因素，如设备价格变动和价格折扣[7-9]、多阶段和多策略租赁[10-13]、设备更新[4-15]、通货膨胀[6-17]、复利[8]、时间约束[9-20]、绩效比[21]等，改善了决策者的决策条件和信息知识，使决策更符合实际投资活动。

已有文献都是在Karp单一设备资产上进行的一系列研究，而实际投资中由于业务需要可能需同时使用多台设备生产。下例子说明多设备租赁问题与单一设备租赁问题的不同：某公司需要同时使用2台设备，但不知道需要使用多长时间，每台设备的购买价格为10，租赁价格为1，公司可选择租赁两台设备、或购买两台设备、或租一台设备再买一台设备等，那么何种租赁策略最划算？按照Karp单一设备租赁模型，把两台设备看成一个整体，得到的最优租赁策略是：前9期连续租赁两台设备，第10期若仍需要使用，就购买两台设备，得到的竞争比为2-1/10=1.9。但这并不是最优策略，事实上公司可采取在前6期每期都租用两台设备，在第7期开始如果还需要使用设备就购买一台设备、再租用一台设备直到第9期结束，当第10期还需要时再买下一台设备的策略，则可得到1.75得到竞争比，显然此策略要优于Karp提出的单一设备租赁策略。由此可知多设备租赁问题与单一设备租赁问题存在着本质上的区别，多设备租赁问题并不是单一设备租赁问题的简单推广。

对于多设备租赁的研究，胡茂林[22-23]假设所需的多设备是连续可分资产，并给出对应的风险控制策略，接着，又将利率因素引入模型，给出存在市场利率的连续松弛多重在线租赁策略。但在投资中，设备往往不是连续可分，而目前尚没有文献对离散多设备租赁问题进行研究。考虑到实际投资的需要，本文给出通胀市场下离散多设备投资的最优方案，给投资者的决策提供一定的理论和现实指导。

2 通胀下Karp的在线租赁策略

某企业需要使用多台设备，但事先并不确定到底需使用设备多长时间，决策者又必须在每期的开始立即做出是继续租赁还是购买该设备的决定，一旦购买某台设备，则以后如还需使用则不必再支付任何费用，那么何种策略是最优的呢？

针对多设备在线租赁问题，假设如下：

(a)在线决策者需要使用某设备m台，每期每台设备的租赁费用为l，购买价格为p；

(b)考虑到实际生活中通胀因素的存在，则设备的租赁和购买价格随时间推移持续上涨，假设每期上涨的比例是ρ(ρ≥0)，称为物价上涨指数；

(c)不考虑除物价上涨指数外的其他因素，如设备的寿命等。

基于假设条件，首先采用Karp最早在“租雪橇”问题中提出的在线算法和竞争分析方法进行研究。Karp在策略中给出在线和离线两种可比投资策略，可供在线者选择策略集为S={S(1),S(2)…}；离线者的不确定策略集为Σ。对于在线者的策略S(t)及离线者的不确定输入σ∈Σ，记其决策费用分别为Coston(σ;t)和Costoff(σ)，如果存在一个与σ无关的常数λ使Coston(σ;t)≤λ*Costoff(σ)成立，则最小的λ称为该在线策略的最优λ-竞争比。

令R(t)表示在线策略S(t)的竞争比，即有：

假设设备实际租赁的时间段为n，若n是已知的称为离线问题，否则为在线问题。显而易见，在该问题中离线者的费用是：

(1)

其中n*满足n*=ln(sρ+1)/ln(1+ρ)，s=p/l。

对于在线者，设策略S(t)表示：前t-1期总是租赁设备，到第t期若还需要则购买设备。此时，在线者选择策略S(t)需支付的费用是：

(2)

根据在线和离线策略的费用及竞争比的定义，易得到策略S(t)的竞争比R(t)为：

进一步，通过在线算法和竞争分析可证明该问题的最优竞争比R(n*)为以下定理2.1。

定理2.1 对于每期租金是l、购买价格是p、物价上涨指数是ρ、设备总单位数是m的在线租赁问题，运用Karp模型得到的最优策略是：前n*-1期都租用设备，到第n*期若还需要即买下设备。对应的最优竞争比是：

R(n*′)=minR(t)

3 风险控制下的多设备在线租赁策略

s.t.0≤mt≤m,t=1,2,…,n且mt是整数

为确定每期购买和租赁设备的数量，我们借助外汇兑换[24]的思想给出以下策略以控制风险获取最优竞争比α，对应的策略称为CR策略：

(i)在前n*期中，当每个租赁期t到来时，如果投资者还需使用该设备，则考虑购买足够数量的设备mt，使得即使以后设备不再使用时仍能保证得到竞争比α；

(ii)前n*期购买设备的总量应等于投资者总共需要的设备数量m，以免投资者如果在n*+1期及以后仍需使用该设备时还要再支付租赁费用。

按照CR策略，不难得出定理3.1。

定理3.1 对于每期租金是l、购买价格是p、物价上涨指数是ρ、设备总单位数是m的在线租赁问题，最优的在线风险控制策略是：当第k(1≤k≤n*)期到来时，投资者考虑购买的设备单位数量是mk，而剩余的m-m1-m2-…-mk单位设备进行租赁。CR策略得到的最优竞争比是：

其中每期购买设备的单位数是：

(3)

证明：用归纳法进行分析。

1)当第一期到来时，投资者考虑购买的设备数量是m1，则剩余的m-m1单位设备进行租赁，根据CR策略法则，有竞争比α满足：

则第一期购买的设备单位数m1是：

2)按照数学归纳法原则，现假设当i=k-1时，有式子(3)成立：

3)现需证明当j=k时式(3)同样成立。

当j=k，即当第k期到来时，投资者考虑购买设备单位数是mk，剩余的m-m1-m2-…-mk单位设备进行租赁，根据CR策略有竞争比α满足：

α=

(4)

对式(4)化简得：

(α-1)ml(1+ρ)k-1=

(5)

根据已知mi(1≤i≤k-1)的表达式，式(5)化成：

由此可得式(3)同样成立：

因此，由数学归纳法原理可得，对于1≤i≤n*均有式子(3)成立。

同时，由CR策略的第二条法则可得：前n*期购买设备的总量应等于投资者共需的设备数量m，即有：

由此可得策略的竞争比α为：

对应每期购买设备的单位数是：

至此，定理3.1证明完毕。

从理论上我们给出每期租赁和购买设备的单位数及其对应的最优竞争策略和竞争比，但可看出理论上所得到的单位数可能都是非整数的。而在实际投资中，购买和租赁设备都是以整数单位进行投资的，因此有必要对理论结果进行调整，设法得到近似的最优解，使得策略更符合实际投资。进一步，对策略CR进行改进得到CRJ策略，具体的调整规则如下：

(i)根据CR策略算出理论上的最优竞争比α及每期购买单位数mk；

(iii)由于规则(ii)中对设备购买单位数都进行取整的调整后，可能到第n*期时总共购买的单位数不等于设备原本总需要的单位数m，此时需要进行第二次调整，分两种情况讨论：

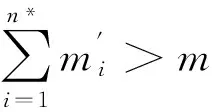
(iv)对所有n*期购买和租赁的设备单位数都进行调整后，得到近似的竞争比α″。

需注意的是，该策略是按照实际投资情况对理论上的最优策略进行的调整，得到近似的CRJ策略的最优性还需进一步验证，但无论如何，本文提出的策略更适应实际投资离散的情形，且能有效分散投资风险和提高竞争比性能，具有一定的现实投资指导意义。

4 算例分析

基于实际投资中物价不断上涨的现象和投资者因生产需要同时使用多台设备的事实，本文以通货膨胀为背景，考虑物价上涨和多设备投资的因素，根据在线算法和竞争比理论构建投资策略，本小节将对模型中的参数分别取不同数值进行算例分析，进一步说明物价指数因素和多设备投资因素的引入对投资者的决策有着重要的影响。

以大型工程公司租赁工程设备为例，某大型工程公司需要某工程设备30台，公司可以按每个设备5万元的价格购买这些设备，也可以按每月每台设备1000元的价格进行租赁，还可以采取购买一部分再租赁一部分设备的策略。已知当前的物价上涨指数是0.02，但是公司决策者并不知道工程什么时候结束，需要使用设备多长时间，那么决策者应该采取何种投资策略才是最优的呢？根据上述问题，采用本文给出的投资策略，则有参数m=30、p=50000、l=1000、ρ=0.02。按照CR策略计算，最优的决策时间是在35个月内完成投资，其决策结果如表1。具体决策过程如下：首先，根据CR策略算出理论上每期购买的单位数mk(见第二列)；然后，按每月设备购买单位数mk的优化规则得到调整后的离散购买单位数(见第三列，按策略调整得总共购买35台设备，而实际只需要30台)，经过第一次调整得到每期的竞争比见第五列；接着，需要进行第二次调整，取竞争比最大的五期调整，调整后每期的购买数量见第七列，对应调整后的每期竞争比见第九列，此时已完成整个优化过程。

在同样的物价水平ρ=0.02下，根据Karp经典“租雪橇”模型即本文第二部分，可得出模型的最优竞争比是2.9216(即是此模型中最优的投资策略结果是事后投资决策最优成本的2.9216倍)。当假设设备是连续可分资产时，根据CR策略可得对应的最优竞争比是1.9728。而本文提出的多设备离散情形下的租赁策略的最优竞争比是2.0933。可看出，我们提出的离散策略效果虽没有理论上连续的结果理想，但明显好于Karp之前的设备整批租赁模型，相比之下，本模型能更好的服务于现实投资决策。

表1 m=30、p=50000、ρ=0.02条件下CR策略和CRJ策略的决策过程

表2 不同参数下CRJ策略的比较和分析

不失一般性，我们对投资模型中的不同参数取不同数值进行进一步分析，对应情况下的投资策略如表2所示。

从表2可看出，当物价指数保持不变时，随着总需要设备单位数的增多，最优竞争比逐渐减小，特殊地，当需要的设备单位数趋于正无穷大时，离散情形下的最优竞争比无限接近于连续问题的最优竞争比。而当物价指数逐渐增大时，最优决策日期相应提前，对应情形下的最优策略竞争比也逐渐增大。这也进一步说明了物价指数和多设备投资因素对投资决策具有重要的影响。

5 结语

基于现实金融租赁市场中物价不断上涨的现象和投资者有时需要同时使用多台设备的事实。本文以通货膨胀为背景，考虑多设备投资、物价上涨等市场因素的在线租赁问题，给出其在理论上最优的在线、离线策略和竞争比，在此基础上考虑实际决策中设备的投资数量需满足整数的条件，进一步对理论数据进行调整，以期获取理论最优策略的一个近似策略。最后通过数值例子分析实际投资的方案和各种参数对投资的影响，结果表明物价上涨因素对多设备的投资决策具有一定影响。

但是，本文给出的离散设备的投资策略由于其需根据CR策略结果进行多次优化，其最优性也难以证明，只能从一般的算例中进行讨论和分析。但可以证明的是，该策略结果优于Karp之前提出的设备整批租赁策略，对离散多设备投资有兴趣的读者可以进一步探讨分析其最优性。

另外，本文的研究仍假设投资者对未来设备的需求信息一无所知，只根据过去和目前的信息作出决策，这往往忽略了某些有用的信息。因此，在今后的研究中，主要是在本文研究的基础上考虑设备的未来需求序列服从某种概率分布的在线策略，使问题更贴近实际。同时，进一步将概率预期下的两种风险补偿模型运用于其它各种租赁问题中，如带租赁合同约束、设备更新问题等，考虑投资者的风险补偿偏好，设计出更有效、实用的在线策略。

[1] Bell T J, Thomas J. Tax benefits of leasing[J]. Economics Letters, 2013, 120(2): 338-341.

[2] Aurora C, Bontas B. Lease financing: A new dual approach[J]. Management Strategies Journal, 2013, 23: 87-96.

[3] Sule O E, Amuni S I.Equipment leasing as a source of finance for small and medium scale entrepreneurs in Nigeria[J]. International Journal of Management Excellence, 2014, 2(3): 247-256.

[4] Karp R. On-line algorithms versus off-line algorithms: How much is it worth to know the future？[C]//Proceedings of IEIP 12th Word Computer Congress. Madrid Spain,September, 1992,7-11.

[5] El-Yaniv R, Knaiel R, Linial N. Competitive optimal on-line leasing[J]. Algorithmica, 1999, 25: 116-140.

[6] Al-Binali S. A risk-reward framework for the competitive analysis of financial games[J]. Algorithmica, 1999, 25(1): 99-115.

[7] Irani S, Ramanatham D. The problem of renting versus buying[J]. Personal Communication, 1998,4(3):6-11.

[8] Bienkowski M. Price fluctuations: To buy or to rent[M]//Bampis E,Jansen K.Approximation and Online Algorithms Berlin Heiderlbery, 2010: 25-36.

[9] Ding Lili, Liu Xinmin, Kang Wanglin. Competitive analysis of online price discount replacement problem[R]//Proleedings of International Joint Conference on Computational Sciences and Optimization, Sanya,Hainan,April,24-26,2009.

[10] 王杨, 董玉成, 徐寅峰,等. 多阶段占线赁购问题与竞争分析[J]. 中国管理科学, 2009, 17(3): 101-106.

[11] Lotker Z, Patt-Shamir B, Rawitz D. Ski rental with two general options[J]. Information Processing Letters, 2008, 108(6): 365-368.

[12] Lotker Z, Patt-Shamir B, Rawitz D.Rent. Lease or buy: Randomized algorithms for multislope ski rental[R]//Proceedings of the 25th Annual Symposium on Theoretical Aspects of Computer Science, Bordeaux,France,February,2008,21-23.

[13] Fujiwara H, Kitano T, Fujito T. On the best possible competitive ratio for multislope ski rental[M]//Asano T,Nakano S,Okamoto Y,et al. Algorithms and Computation, Behin Heidelbery:Springer,2011: 544-553.

[14] 辛春林, 陈剑, 刘天亮. 基于凸情形下在线设备更新问题的竞争分析[J]. 系统工程理论与实践, 2009, 29(11): 145-151.

[15] 张永, 张卫国, 徐维军. 在线设备更新问题的竞争策略及其风险补偿模型[J]. 中国管理科学, 2010, 18(2): 113-119.

[16] 徐维军, 胡茂林. 基于物价指数上涨的最优在线租赁决策模型[J]. 系统工程理论与实践, 2013, 33(3): 1-10.

[17] 刘幼珠, 徐维军, 胡茂林. 通胀市场下的风险补偿在线租赁策略设计[J]. 运筹与管理, 2013, 22(4): 175-181.

[18] Yang Xingyu, Zhang Weiguo, Zhang Yong, et al. Optimal randomized algorithm for a generalized ski-rental with interest rate[J]. Information Processing Letters, 2012, 112(13): 548-551.

[19] Khanafer A, Kodialam M, Puttaswamy K. The constrained ski-rental problem and its application to online cloud cost optimization[R]//Proceedings of 2013 IEEE INFOCOM, Turin,April 14-19,2013:1492-1500.

[20] Epstein L, Zebedat-Haider H. Rent or buy problem with a fixed time horizon[M]//Chatterjee K,Sgall J. Mathematical Foundations of Computer Science 2013, Berlin Heidelbery:Springer,2013: 361-372.

[21] 杨兴雨, 张卫国, 徐维军,等. 基于绩效比和合同约束的多阶段在线租赁[J]. 中国管理科学, 2014, 22(2): 94-100.

[22] 胡茂林. 可分资产的在线租赁策略及其竞争分析[J]. 系统工程理论与实践, 2011, 31(1): 144-150.

[23] 胡茂林, 徐维军, 刘幼珠. 存在市场利率的连续松弛多重在线租赁问题[J]. 管理科学学报, 2014, 17(9): 29-39.

[24] El-Yaniv R, Fiat A, Karp R, et al. Optimal search and one-way trading online algorithms[J]. Algorithmica, 2001, 30(1): 101-139.

Competitive Strategy for On-line Multiple Devices Leasing in an Inflation Market

XU Wei-jun1, LIU You-zhu1, CHEN Xiao-li1, HU Mao-lin2, GAO Li3

(1.School of Business Administration, South China University of Technology, Guangzhou 510641, China;2.School of Mathematical Science, Huaiyin Normal University, Huaian 223300, China;3. School of Mathematics, South China University of Technology, Guangzhou 510641, China)

There exist massive phenomena of leasing multiple devices at the same time in the real leasing market. And the biggest problem what the manager faces is to optimize the combination of multiple devices on-line leasing in order to reduce the decision-making cost. However, inflation further increases the difficulty. In this paper, risk control model for the multiple devices leasing problem is put forward using the method of on-line algorithm and competitive analysis, and the impact of inflation on decision-making is analyzed. Firstly, the on-line and off-line strategies are proposed respectively for the multiple devices leasing according to the model of Karp’s with the factor of inflation. Then to improve the competitive ratio in Karp’s model, the risk control strategy which we call the CR strategy is discussed in theory with the hypothesis that the device is continuous separability. Furthermore, when consider that the number of devices investing in real decision-making must be integer, the risk control model is reconstructed and optimized to gain a new approximate strategy-CRJ strategy. Finally, the optimal competitive performance of the strategy is discussed and illustrated by numerical analysis, which shows that the competitive performance of on-line strategy is affected by the fact of inflation and the ways of investing. More, a new idea in multiple devices leasing problem is given in this paper.

inflation; multiple devices leasing; on-line algorithm; competitive analysis

1003-207(2016)02-0069-07

10.16381/j.cnki.issn1003-207x.2016.02.009

2013-12-15；

2015-03-11

国家自然科学基金资助青年项目(71471065)；中央高校基本科研业务费专项资金资助(2012ZZ0035)；中央高校基本科研业务费自然科学类项目(x21xD214183W)

简介：徐维军(1975-)，男(汉族)，宁夏人，华南理工大学工商管理学院研究员，研究方向：在线金融算法,E-mail:xuwj@scut.edu.cn.

F224

A