数字式正交包络检波算法实现

郭瑞鹏,宫 政,王海涛,徐 君,仲光明

(南京航空航天大学 自动化学院, 南京 211106)



数字式正交包络检波算法实现

郭瑞鹏,宫 政,王海涛,徐 君,仲光明

(南京航空航天大学 自动化学院, 南京 211106)

针对超声相控阵检测系统中的数据采集与处理模块，设计了数字式正交包络检波算法。通过取包络，在保留超声脉冲回波信号幅值信息的基础上，将射频信号转换为基带信号，降低了采样率，节约了存储空间。同时，将正交包络检波从模拟域转换至数字域，提高了包络检波的效率及精度，改善了整个检测系统的性能。

超声相控阵；正交包络检波；数字式

超声相控阵检测不同于传统的超声检测，它使用多阵元探头，将原有的单一晶体分割为许多独立的小晶体，每一个晶体的尺寸符合一定的波动条件[1]。当用同一脉冲信号激励相控阵探头时，各阵元发出的超声波相干并在空间叠加形成特定指向和聚焦特性的波束。根据设定的聚焦法则，计算出相应的激励延时，运用电子技术控制电脉冲序列激励各阵元，其发射的超声波可在被测时间内指定点聚焦，该合成波束在声阻抗突变处(如缺陷位置)发生反射，反射的回波信号以一定时差返回相控阵探头各阵元；按照相应的延时规则进行延时补偿再叠加合成，便可将合成结果以适当形式显示出来[2]。超声相控阵技术，就是通过控制各个独立阵元延时的方式，生成不同指向性的超声波波束，并产生不同形式的声束效果[3]。

对于超声相控阵检测系统而言，多路脉冲回波信号包含了成像处理需要的所有信息；将每个阵元接收到的回波信号进行叠加合成，即可获得全部的回波信息。但由于相控阵探头阵元的排布，从缺陷位置返回的超声波到达超声阵列换能器每个阵元的声程不同，需要对各路超声脉冲回波信号进行延时补偿及声束形成处理，才能使目标点上的回波信号相位相同，信号强度增大，同时，其他位置上的超声脉冲回波信号强度被减弱[4]。

上述的超声相控阵信号接收算法，只进行了简单的信号处理，叠加之后的信号属于射频信号，其频率和超声阵列换能器中心频率相近，要想获得回波信号中所包含的全部信息，则必须提高整个系统的采样率。如果不对回波信号进行处理，势必造成整个检测系统成本以及实现难度的增加。为此，笔者针对超声相控阵检测系统中的数据采集与处理模块，设计了数字式正交包络检波算法。

1 数字式正交包络检波方法

1.1 数字式正交包络检波原理

超声相控阵检测系统中，对于后期回波信息的数据处理，只需要保留超声脉冲回波信号中的幅值及相位信息，便足以获知缺陷的相关情况。因此，可以对叠加后的超声脉冲回波信号进行取包络处理。这样，便可以在保留超声脉冲回波信号幅值信息的基础上，将射频信号转换为基带信号，降低系统采样率，缓解检测系统存储空间的压力。

传统的超声相控阵检测系统通常采用模拟正交包络检波进行设计[5]。这种包络检波的不足之处在于模拟器件本身的精度有限，会降低超声脉冲回波信号的检波处理效果，造成一定程度的失真，无法达到整个超声相控阵检测系统的检测要求。为了提高包络检波的效率，改善整个检测系统的性能，笔者采用了数字式正交包络检波技术，将传统的包络检波设计从模拟域转换到数字域，其原理框图如图1所示。图中，ωr为本振信号频率，I、Q分别为经过混频、低通滤波处理后的两路正交的脉冲回波信号，A(nTs)为经过A/D采样转换之后的超声脉冲回波的幅值信息。

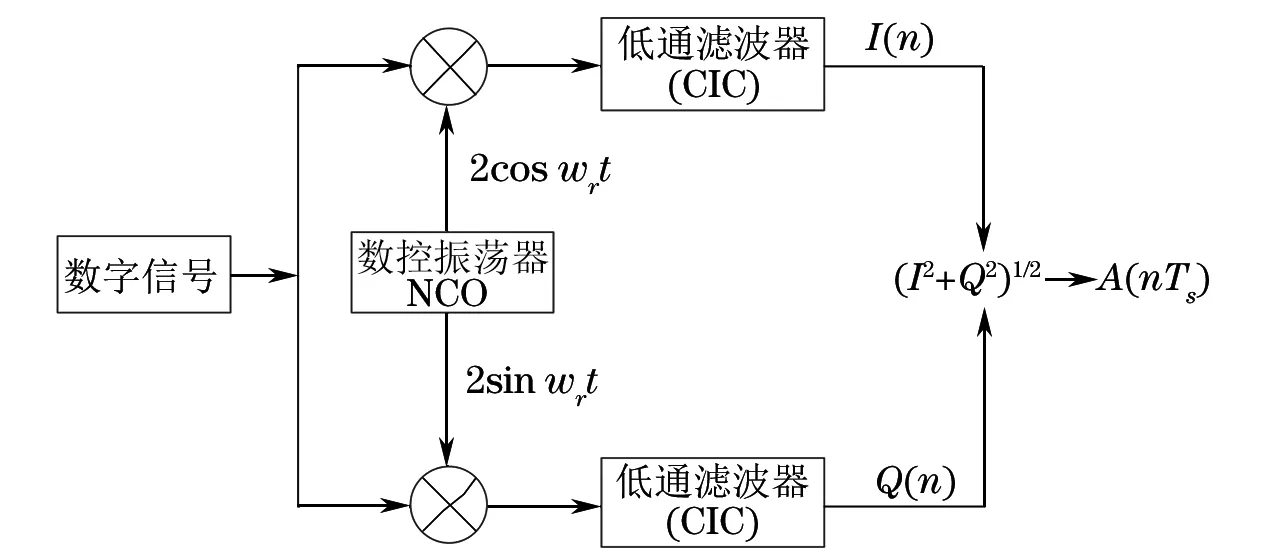
图1 数字式正交包络检波原理框图

笔者采用的是线性超声阵列换能器，其阵元按照等间隔依次排列，并由收发电路根据不同的聚焦法则进行激励和接收。系统中第k个超声阵列换能器阵元接收到的中频信号为：

(1)

式中:A(t)为超声脉冲回波的幅值信息;ω0为超声脉冲回波的频率;Φ(t)为超声脉冲回波的相位信息。

经过A/D采样转换之后，可得：

fk(nTs)=A(nTs)cos[ω0nTs+Φ(nTs)]=

(2)

式中:AI(nTs)=A(nTs)cosΦ(nTs)为同相分量;AQ(nTs)=A(nTs)sinΦ(nTs)为正交分量;Ts=1/fs为采样间隔;fs为采样频率，由奈奎斯特采样定理可得fs>2ω0，但在实际应用过程中，一般要求fs>4ω0。

由图1可知，经过A/D采样后的回波信号与两路信号相乘，分别是2coswrnTs、2sinwrnTs，它们被称为I、Q的本振信号，且相互为正交关系，并且在设计中，选取ωr=ω0。经过混频、低通滤波后，可得：

Ik=LPF[fk(nTs)×2coswrnTs]=

AI(nTs)cos(ω0-ωr)nTs-

(3)

同理可得：

Qk=Ai(nTs)sin(ω0-ωr)nTs-

(4)

经过进一步数学运算,可得：

(5)

式中：下标k表示超声相控阵探头中的第k个单元；AI(nTs)，AQ(nTs)分别为经过A/D采样转换之后的超声脉冲回波I信号和Q信号的幅值信息。

可见，合成声束经过数字式正交包络检波后，便可以得到其幅值大小。在推导过程中，本振信号与脉冲回波信号频率相等，但在实际应用过程中，并不要求两者完全相等，因此可以降低对本振信号设计的难度。

与模拟正交包络检波相比，本振信号、混频、低通滤波器等功能的设计均是在数字域完成的，其中本振信号由数控振荡器(NCO)产生，低通滤波器选用的是积分级联梳状(CIC)滤波器，二者可以保证本振信号相位的正交性以及滤波器系数的一致性。因此，数字式正交包络检波的精度远高于采用传统方式的模拟正交包络检波方法。

1.2 数字式正交包络检波设计如前所述，对于超声相控阵检测系统，只需要利用被检工件回波信号的幅值及相位信息，便可在成像过程中对缺陷进行简单的定位及显示。因此，正交包络检波器的设计尤为重要。包络信号相对于回波信号而言属于慢变信号，可以降低采样频率，缓解系统的存储压力，便于后续处理。该小节即针对图1中描述的数字式正交包络检波的具体实现展开论述。

对于声束合成之后的信号，首先需要将其和一对正交的载波信号进行混频操作，即本振信号2coswrnTs、2sinwrnTs。采用了数控振荡器(NCO)来实现两路正交的载波信号，它是实现数字信号处理(DSP)、频移键控(FSK)、数字调制解调器的重要部件[6]。

数控振荡器可以产生正弦波形，用来综合时间离散和取值离散，Altera公司提供的NCO IP核可以实现数控振荡器的功能，其生成的正弦波可以表示为：

(6)

式中：fO为未调制输出频率；fFM为调制输出频率；T为周期；A=2N-1；N为10～32之间的任意整数;ΦDITH为模块内部不稳定而引起的相位杂散(噪声)；ΦPM为输出正弦波的调制相位。

输入相位增量ΦINC决定了fO输出值的大小，其具体计算过程如下式：

(7)

式中：M的含义为累加器的精度；fCLK为数字信号处理电路的系统时钟频率。

当ΦINC=1时，fO值为最小值，也称为频率分辨率，即fO=fCLK/2M(单位赫兹)。

由此可见，数控振荡器输出信号的频率分辨率取决于M，且与M成反比例关系。文中选取的M值为32。由于使用的超声阵列换能器的中心频率为4 MHz，因此数控振荡器的输出频率为4 MHz，即fO=4 MHz，可以得到输入相位增量的值为：

(8)

Altera公司提供的NCO IP核相关接口参数,如表1所示[7]。

表1 NCO IP核接口说明

2 试验结果

图2给出了本振信号的仿真效果。由图可知，两路信号频率为4 MHz，且相位差为90°，满足正交关系。

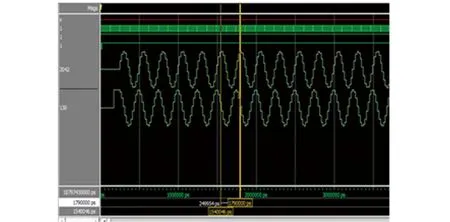
图2 数控振荡器仿真波形

声束合成之后的信号与两路本振信号进行的乘操作，称之为混频处理，得到I、Q两路信号，分别由一个低频分量(频率为ω0-ωr)和一个高频分量(频率为ω0+ωr)组成。这里,只需要对混频之后的低频信号进行后续的处理，因此，需要设计一个低通滤波器用来抑制高频分量[8]。

为了实现低通滤波效果，通常采用多级CIC滤波器。文章选取级数为3、速率变换因子为4、差分延时为2的CIC抽取滤波器。为了验证滤波器的效果，对其进行低通滤波仿真测试。由于本振信号的频率为4 MHz，可选取频率为3.5 MHz的正弦波分别和两路本振信号做混频处理，得到的结果为0.5 MHz的低频信号以及7.5 MHz的高频信号。经过CIC抽取滤波器后，输出信号为0.5 MHz的低频信号，如图3所示。其中第一、三路分别为混频后的I、Q两路信号，第二、四路分别为第一、三路经过低通滤波后的低频信号。

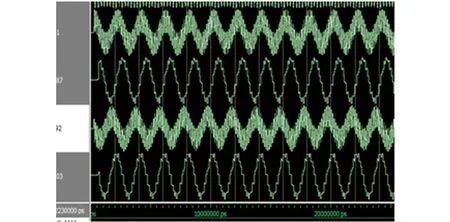
图3 3级CIC抽取滤波器仿真波形

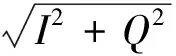
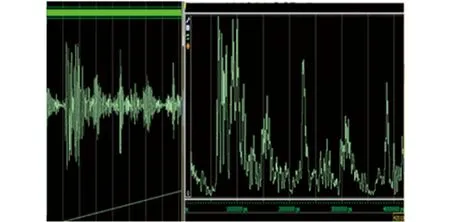
图4 数字式正交包络检波仿真波形

3 结语

采用数字式正交包络检波技术，在提取出脉冲回波信号幅值信息的前提下，大幅降低了超声脉冲回波信号的频率，减少了数据量。试验结果表明，数字式正交包络检波能够成功提取包络信号，且提取效果与精度良好。

[1] 沈立军. 超声相控阵收发电路设计与关键技术研究[D].南京：南京航空航天大学, 2014.

[2] 郭艳. 超声相控阵检测系统成像技术研究[D].南京：南京航空航天大学, 2014.

[3] 程继隆. 超声相控阵检测关键技术的研究[D].南京：南京航空航天大学, 2010.

[4] 李衍. 超声相控阵技术 第一部分 基本概念[J]. 无损探伤, 2007, 31(4): 24-28.

[5] 吴远斌. 一种数字式正交检波器的设计[J]. 电子科学学刊, 1997(1): 68-71.

[6] 董亮, 汪敏, 高亦菲,等. 基于NCO IP core的Chirp函数实现设计[J]. 现代电子技术,2009,20(20):20-22.

[7] 孙玉梅. 基于FPGA的FSK调制解调器的设计及实现[J]. 电子科技, 2009, 22(5): 38-39.

[8] 窦建华, 梁红松, 胡敏,等. 一种改进的CIC抽取滤波器设计[J]. 系统工程与电子技术, 2008, 30(5): 984-986.

The Realization of Digital Orthogonal Envelope Detection Algorithm

GUO Rui-peng, GONG Zheng, WANG Hai-tao, XU Jun, ZHONG Guang-ming

(College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)

A digital orthogonal envelope detection algorithm for data acquisition and processing module of the ultrasonic phased array testing system is designed. By taking envelope, the amplitude information of ultrasonic pulse echo signal is kept, and the RF signal is converted to baseband signal. Accordingly, the sampling rate and the system storage space can be reduced. At the same time, by converting the orthogonal envelope detection from analog domain to digital domain, the efficiency and precision of the envelope detection are improved, and the performance of the whole detection system is enhanced.

Ultrasonic phased array; Orthogonal envelope detection; Digital

2016-06-22

郭瑞鹏(1981-)，女，博士,讲师,主要从事相控阵、激光超声方面的研究工作。

王海涛，E-mail: htwang@nuaa.edu.cn。

10.11973/wsjc201612002

TG115.28

A

1000-6656(2016)12-0006-03