威廉·博尔科姆现代钢琴作品中点描技法的音响元素量化与对比研究——以《十二首钢琴练习曲》第一首为例

威廉·博尔科姆现代钢琴作品中点描技法的音响元素量化与对比研究
——以《十二首钢琴练习曲》第一首为例

张 放

文章选取美国当代作曲家威廉·博尔科姆钢琴作品中点描技法的音响元素作为研究对象，借助统计学、和声力学等理论对《十二首钢琴练习曲》（12 Etudes for Piano）第1首中的力度、时值、演奏法以及音高参数进行了量化分析，进而观察作品中的材料特征、音响发展和结构布局，解读出作曲家在创作中利用音响元素实现了全局设计。

［美］威廉·博尔科姆（William Bolcom 1938-）；《十二首钢琴练习曲》第一首；和声力学；音响元素；结构布局

为了获得丰富多彩的钢琴音响音色变化，当代作曲家在前人的基础之上迈出了坚实的一步。在宏观层面上，作曲家不断地尝试拓展不同的弹奏技巧、演奏法，并为此积极改进记谱法和乐器功能；在微观层面上，作曲家在许多钢琴作品中融入了微妙细致的层次变化，形成了力度、音值、和声张力、演奏法等音响对比关系。①姚恒璐：《现代音乐分析方法教程》，长沙：湖南文艺出版社2003年版，第74页。然而，这些作曲家在处理钢琴音响音色时，总有隶属于自身独特的手法和理念，所以对于音乐研究者而言很难设定一种适用于所有作品、具有高度程式化的分析方法。如在点描式、镜像、块状织体为主的音乐作品中，我们发现用传统的分析方式无法解释这些音响元素的存在意义，也无法理解作曲家在编排这些元素时的内在逻辑。为此，多年来许多学者进行了大量研究工作，试图通过量化计算与数据分析的方式对乐曲的内容进行剖析。如高为杰先生1986年起即针对和声力学发表了相关研究成果，给出了音高集合纵列的分类及和声张力效应定量化分析的具体方法。此后，王文先生于1992年发表《模糊数论对和声力学研究的梯度级开发》一文，以非精确定量的形式对和声力学的相关参数进行了表述。冯勇先生2013年发表的《和声力学研究——“拍音论”为基础的“和声体”张力定量化分析》一文则是建立了“和声体”张力效应定量化分析理论及方法，对音程、和弦、音集等重要参数进行了量化分析。

本文选取威廉·博尔科姆的钢琴作品《十二首钢琴练习曲》第一首作为研究对象。这首作品创作于1959，是博尔科姆早期作品中的经典之作，在众多现代钢琴点描技法的创作中具有典型性。在此作品中，作曲家通过对演奏法、力度、音符时值、音质等元素的不断变换，将音色切割成零碎的单音“色彩点”与音集“色彩块”，再将它们串联后形成横向的“色彩线”。为了更加清晰直观地分析博尔科姆在不同音响元素上的运用，本文对和声、时值、力度、演奏法等元素进行量化处理，进而一一罗列、逐步解析，犹如把音乐作品放在显微镜或像照X光片一样来剖析它们内在的某种联系。具体四个分析步骤如下：（1）参考点描技法中音集、力度等内容，对作品的音高材料进行音点分组②［美］阿伦·福特：《无调性音乐的结构》，罗忠铭译，上海：上海音乐出版社，2009年，第76页。；（2）将几种不同的音响元素进行分层，并制定具体的量化方法；（3）将得出的各音响元素量化值处理后进行横向比较；（4）总结各音响元素数据的关联性，并阐述其在结构中的作用与意义。

谱1 《十二首钢琴练习曲》第一首③音点分组

一、音响元素量化方法

这首作品在整体结构布局上简短而精炼，全曲共23小节。整体速度平稳缓慢，拍号转换并不频繁，以3/4拍子为主。在进行音响量化之前，首先需要将全曲23个小节中的所有音高素材进行分组。如谱1中所示，所有单音及音集均具有明确的力度和演奏法标记，并且时值变化频繁，易于辨认。其分组方法主要通过对音高、力度、演奏法这三个方面进行抽离和归类后，将其分为音色及音质各异的154个音点。在谱1中显示了第1至8小节的单音和音集分组情况。

对全曲音集进行分组后，再从微观上对音响进行分层处理，可以得出四个不同维度的层次。第一层是力度维度，表现为从ppp至fz的十一个层次；第二层是音符时值，以十六分音符为基础单位排序出色点与色块的时值容量；第三层维度则是演奏法的动力值；第四层为音集的张力度。为了直观准确地了解这些元素之间的关系，测量它们之间相关性的程度，接下来是制定几种音响元素具体的量化方法。

（一）力度值量化

作曲家通常在钢琴作品中组合和运用变化多端的力度与强度，试图在单个音符、乐思或乐句的情绪变化中捕捉到力度所带来的音响明暗和情感张力。此曲中的力度层次以弱区音量为主，整体音响的进行以轻松、灵巧、神秘的氛围慢慢展开。其中力度层次变化最为频繁，最多时在1小节内多达9个“纯力度标记”（不包括渐强渐弱、重音和保持音）。这种力度的处理源于威伯恩的点描式音乐技法，此技法曾为整体序列音乐的形成奠定了基础，但通过分析可以看出博尔科姆很明显地回避了将力度等元素进行严格序列的安排，更多地是对音色和音响的挖掘和尝试。除横向音点、音块外，纵向多声部之间也始终保持着频繁的力度对比，在声部和音区之间形成了丰富细腻的层次感。本曲中可以看出点描性织体与密集的线状织体的并置与结合，所形成的音色特性是不同的，其直观表现为“点与线”并置的织体形态，即相互融合又各自独立。在表1中，我们将此曲中出现的十一种力度层次变化进行了量化设定。

表1 力度量化对照表

从曲中所有分组的音集与单音的力度层面来看，其中只有少数音点没有专属标记任何力度，在量化时则延用前一位音点的力度，如前一位音点力度为突强类（mfzfz）标记时，则延用同一声部前一位的标记。图1中显示了将154个音点进行量化后的力度分布和密集度情况，从中可以看出，所有音点的力度值在-1至0的区间内最为密集，其他力度值相对比较分散。

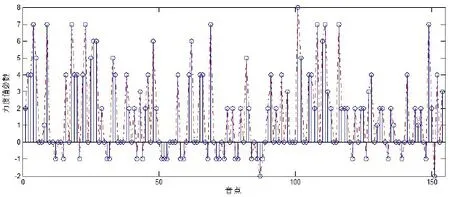
图1 《十二首钢琴练习曲》第一首中154个音点的力度值

（二）时值量化

下面同样将音符的时值进行量化，首先我们需要设定一个相对合理的时值作为标准参数。因需要和其他元素进行比对，所设定量化基础单位的高低必须能够体现与其他元素在格度上取得相对的平衡，本文尝试将十六分音符设定为计算标准单位，如：一个十六分音符=V1.0（V=Value即时值）。此曲中时值最短的音符为六十四分音符，如果按照十六分音符为基础刻度，那么六十四分音符的量化值则为V0.25，以此类推。除常规的量化外，有时会有一些特殊情况，如三连音、五连音等非常规量化方式。另外，许多情况下音符带有延音连线，所以需要将所有时值相加。表2显示了《十二首钢琴练习曲》之一中的时值特殊量化对照，如第17音点：附点八分音符+八分音符+三连音十六分音符之一，所产生的量化时值为V3+V2+V0.66=V5.66。将此曲中所含154个音点的时值进行相关量化，再将延音部分相加，得出时值音点序列（整体数值请参看后文的音响元素对比）。

表2 《十二首钢琴练习曲》第一首非常规时值量化方法

（三）演奏法动力值量化

演奏法在实际演奏当中同样会产生很强的动力感，与其他元素相辅相成，相互依托。演奏法可以直接影响音色及音响的质感，如在极断（重断）情况下，音响往往非常尖锐并带有强烈的冲击性，敲击性较强，而在连奏时则尤为抒情或宽广。将演奏法进行量化时需要考虑力度的影响因素，其主要可以分四类：连奏型、连断型、断奏型、极断（重断）型。在对演奏法的动力值进行量化时，需要考虑两个问题：（1）在相似力度范畴中，演奏法相同时动力感几乎相同，所以在制定基础动力值时将相似的力度如：p与mp给出相同数值；（2）将四种不同演奏法的数值进行按比例分配，连奏动力较弱+0.25、连断+0.5（0.25x2）、断+1（0.25 x 4）、极断+1.5（0.25 x 6）；3）其次是附加值的处理，将几种不同的重音记号、forzando记号、保持记号进行量化，如保持记号为+0.25、重音等记号+0.5（0.25x2），如同时具有多项记号是将数值相加。在此基础上，尽管有时连奏的mp在动力值上可能会比p的值低，但在动力性的角度上这种比例是合理的。

（四）音集张力值量化

在现代音乐中，对于判别和声中的紧张度一直来说都是一个难题，用传统三音叠置和调性中心的方式解释各音程组合之间协和度的高低显然不能适用于所有现代音乐创作。而事实上在聆听这些作品时，和声与音程在进行中呈现了明显的起伏变化，它们之间的张力变化和层次极为丰富，仅依靠听觉感受是无法解释清楚的，必须借助一种现代的定量分析的方法对每一个和弦和音程的紧张度和张力值进行研究，从而得出更为科学的测量结果，在理论层面更为有依据和说服力。本节中对于和声力学的定量分析的理论依据来源于高为杰先生的《和声力学研究——论音高集合纵列的分类及和声张力效应定量化分析》④高为杰：《和声力学研究——论音高集合纵列的分类及和声张力效应定量化分析》，《音乐探索》l986年第3期，第3页。。此研究认为和声关系可以由五度相和作为基础，将十二个音按同向传递而形成一个周而复始的循环圈，也可以说借鉴五度相生律的理论来考量音与音之间的关系。通过对此理论的研究和应用，将《十二首钢琴练习曲》之一中的154个音点进行了详细的分析验证，借以得出音集所蕴含的“静态”与“动态”力学两个层面的张力特征。此曲中的音集“静态”张力值共154个，而音集“动态”则为前后两组音集（张力值）之间的张力差，称为“张力效应”，共153个数值序列（见图2和图3）。

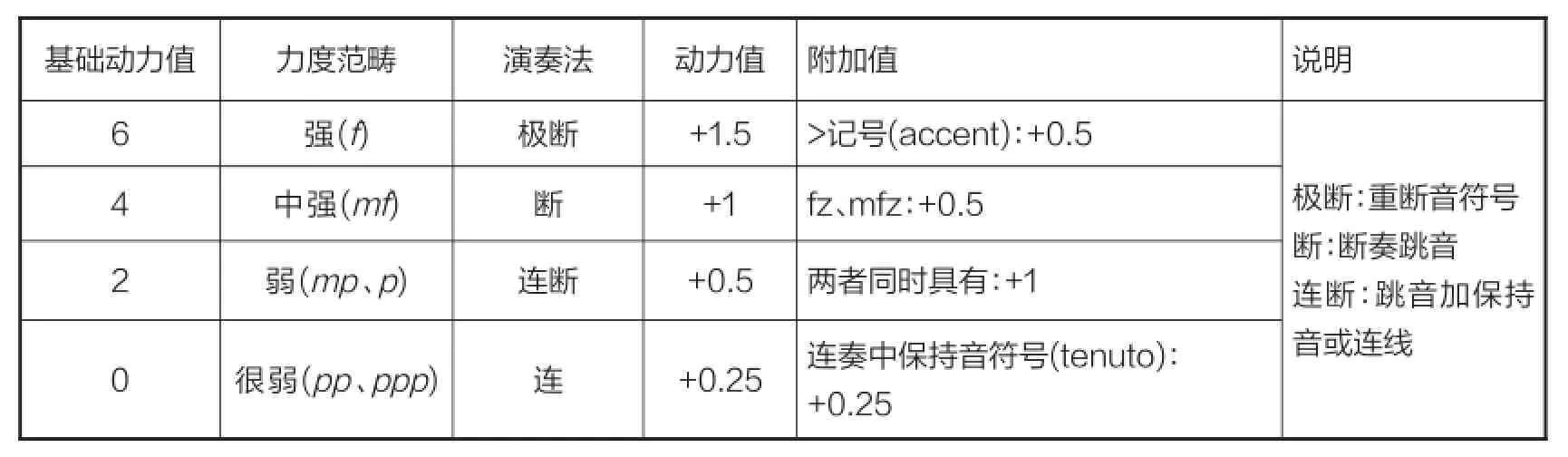
表3 演奏法量化规则

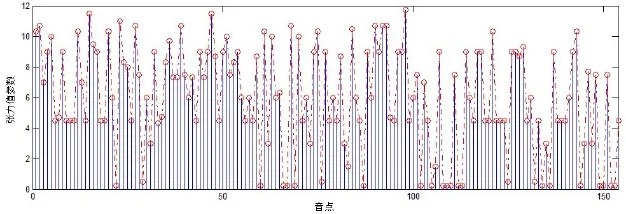
图2 音集“静态”张力值参数

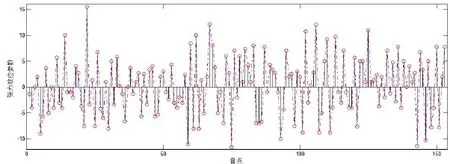
图3 音集“动态”张力效应参数

将上述四种音响元素量化后，所得出的各类数值可以进行横向对比研究，继续探究它们之间的内在联系。博尔科姆在此类作品中将力度、时值、和声、演奏法等作曲手法进行特殊处理，如在《十二首钢琴练习曲》之十一、十二，另一部作品《十二首新钢琴练习曲》（12 New Etudes for Piano）之三中，都蕴含大量的点描式音响变化。我们有理由相信在这些作品中，演奏法与力度的结合、时值与力度的相互作用等在音乐结构和情感表达方面起到了至关重要的作用。

二、音响元素对比与结构关系

（一）序列对比算法简析

在音响元素量化的基础上，为了进一步对比分析这些数值序列之间的潜在关联，找出乐曲内部暗藏的逻辑，本文引入了数理统计理论中的相关系数概念。通常来说，相关系数是衡量两个序列之间线性相关程度的重要指标，它由数学家卡尔·皮尔森（Karl Pearson 1857～1936）在1880年代提出的，现已广泛地应用于科学的各个领域。在相关系数的计算中，通常以rxy表示两个样本的相关系数，其具体的计算公示如图4。⑤孙禄杰、柏满迎：《相关系数与连接函数》，《统计与决策》2006年8月（下），第4页。

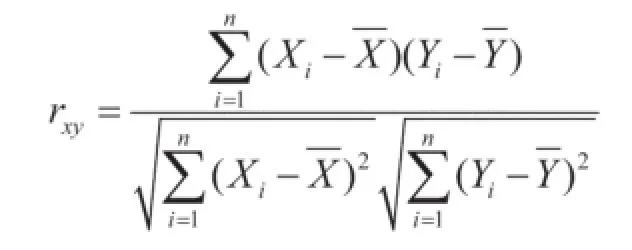
图4 相关系数计算公式

图4中，N代表序列的长度，Xi代表x序列中的第i个数值，X代表x序列平均值，Yi代表序列中的第i个数值，Y代表y序列平均值。计算所得的数值介于-1与+1之间，其含义如下：

1.当r〉0时，表示两变量正相关，当r〈0时，表示两变量为负相关。当|r|=1时，表示两变量为完全线性相关即函数关系。当r=1时，称为完全正相关，而当r=-1时，称为完全负相关。当r=0时，表示两变量间无线性相关关系。

2.当|r|≥0.8时，可视为高度相关；当0.5≤|r|〈0.8时，可视为中度相关；当0.3≤|r|〈0.5时，视为低度相关；当|r|〈0.3时，说明两个变量之间的相关程度极弱。

在本文中将分别设定乐曲的张力值、力度值、时值、演奏法、张力效应、力度效应（效应：是指前后两组力度值相差）这六组音点序列为X序列和Y序列，进行两两比对，试图找出这些音点序列之间的关联并将这些关联程度进行量化分析。

（二）音响序列对比分析

1.张力值与力度值对比

在本文中计算得出的张力值是每一组音级集合作为和声产生的紧张度量化数据，而力度值是根据乐曲中作曲家标记的频繁转换的力度标记所产生的音色的变化量化数据，这二者都是乐曲音响参数的重要体现。根据前面计算得到的结果，分别将两个时间序列在时间点坐标上进行排列，其效果如图5所示。

从图5中可以看到，由于两个序列的波动范围具有较大的差异，直接通过原始数值进行对比的话并没有实际意义，为此本文对向量数据进行归一化处理（见图6）。

在图6的公式中，Xi、Yi分别为归一化转换前、后的序列数值，Ymax、Xmin分别为样本的最大值和最小值，Ymax、Ymin为归一化之后序列的上下限，本文设定的归一化区间为0至1。需要指出的是，归一化处理后的序列并不会影响到相关系数的计算。

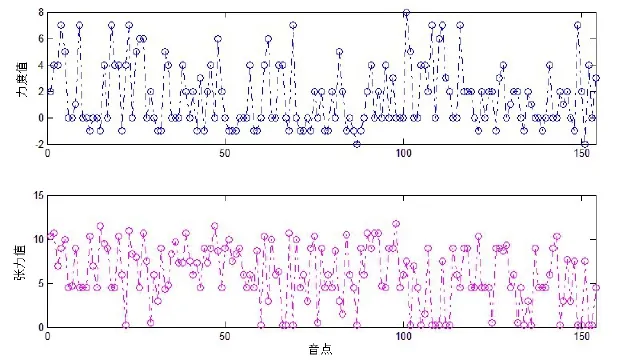
图5 力度值与张力值

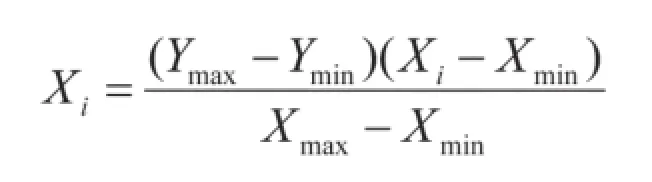
图6 序列归一化计算公式

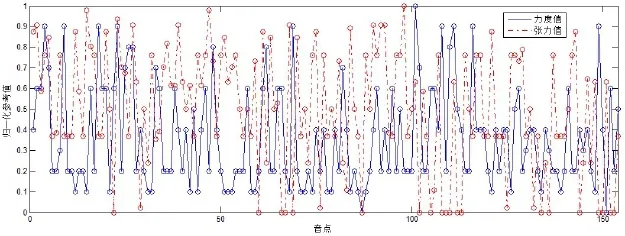
图7 力度值与张力值合比对

在对力度值、张力值序列分别进行归一化转换之后即可将二者放在同一个坐标系中进行比对，其效果如图7所示。

经过相关系数计算后得到这两个序列的相关系数为-0.1549，可以判定，从包含154个音点的整体音集序列上看，力度值和张力值并不存在相关性。考虑到作曲家对于全曲不同部分的处理手法会有所不同，接下来将序列的前150个音点分成15个子序列，每个子序列10个音点，然后将力度和张力相同位置对应的子序列分别进行相关系数计算，从而可以得到一组包含15个数值的序列，如图8所示。

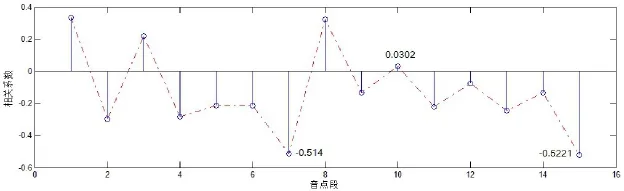
图8 力度值与张力值子序列相关系数变化曲线

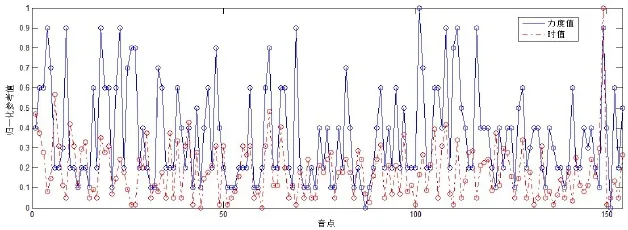
图9 力度值与时值归一化参考值对比

从图6中可以看到，在这15对子序列中，有4对呈现正相关，但是相关性均小于0.4，可以视为低度相关或者不相关，其中以第十组序列的相关性最弱，为0.0302。在11对负相关的子序列中，多数处于-0.3以内，即为低度的负相关，但是在第7组和第15组位置上出现了超过-0.5的中度负相关情况。从出现的位置上看，相关性最弱的第10组子序列恰好处于全曲的黄金分割点位置，而相关性最强的第7点和第15点则位于乐曲的中心和结尾⑥宋廷山：《相关系数统计量的功能及其应用探讨——以SPSS为分析工具》，《统计教育》2008年第11期，第27页。。

2.力度值与时值比较

根据前面计算得出的力度值与时值时间序列，归一化后在同一坐标系中展示的形态如图9所示。

从这两个各包含154个音点的时间序列初步比较图来看，二者总体上并没有明显的相关性，通过计算得到相关系数为0.2596，属于极弱的相关。为了进一步比对不同音点段的相关性变化，接下来仍然将序列的前150个音点分成15个子序列，每个子序列10个音点，然后将相同位置对应的子序列分别进行相关系数计算，得到的相关系数序列如图10所示。

从图中可以看出，分段比对的序列相关性明显较强，第一对子序列就呈现出了-0.697的中度负相关。在第10段时达到了整体的相关系数峰值：0.8791，为强相关，而此处恰恰是涵盖了乐曲黄金分割点的音点段位置。为了进一步证明力度值与时值的相关程度，我们提取出乐曲黄金分割点（第95点）前后的20对音点序列，放大后如图11所示。

从图中可以看出，两个音点子序列的波动形态非常接近，尤其是在91至95音点区间内最为相似，此后便逐渐减弱。为了进一步寻求相关度高的音点子序列，我们对全曲的音点序列进行了更加细致的观察比较，发现除了在黄金分割点周围出现相似度极高的音点序列之外，在第56至65点的音点序列位置也出现了非常相似的情况，而此处正是负黄金分割点位置（第58点），如图12所示。

通过相关系数计算得出，从56至65音点的子序列对之间的相关系数为0.9062，为全曲的最大值。

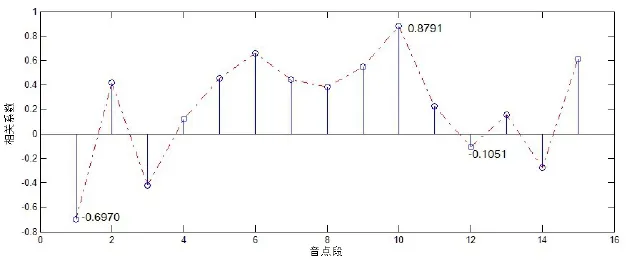
图10 力度值与时值子序列相关系数变化曲线

图11 力度值与时值：第85-105音点归一化参考值

3.时值与演奏法比较

根据前面计算得出的时值与演奏法音点序列，归一化后在同一坐标系中进行逐段比对。通过观察和计算可以发现，虽然二者总体上仍然属于极弱的相关，但是在乐曲的黄金分割点和负黄金分割点位置前后的子序列对上表现出了较强的相关性。其中黄金分割点位置前后（从91至100音点位置前后）的音点子序列比对效果如图13所示。

从图中可以看出，在黄金分割点前后两个子序列表现出了较强的相关性，从91至100音点位置的音点子序列对之间的相关系数为0.5464，属于中度相关。而如果进一步缩小比对区间，聚焦在黄金分割点位置前后共三个音点时（即94、95、96这三个音点），两个子序列的形状更加接近。接下来对乐曲的负黄金分割点位置前后（从56至65音点位置前后）的音点子序列进行比对，效果如图14所示。

从图中可以看出，二者的相关程度更加明显，计算得到的相关系数为0.8333，属于高度相关。

4.其他音点序列比较

随后，我们又以同样的方法将音点之间的动态特征，如将音集动态的张力效应、力度效应数值序列进行了相关性比较。通过从序列图形上观察，这些参数的音点序列无论是从整体看还是从局部看都没有明显的相似性，计算结果也显示这些序列各段的之间的相关系数都较低，可以判断这些参数之间没有明显的关联。

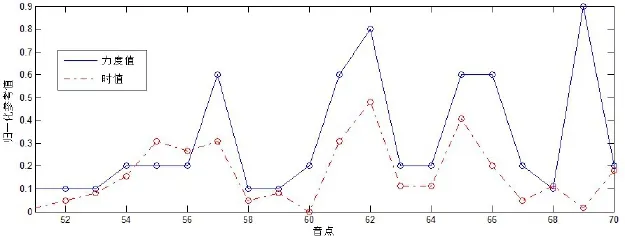
图12 力度值与时值：第50-70音点归一化参考值

图13 时值与演奏法：第80-105音点归一化参考值

三、结论

在现代音乐中应运而生的新的作曲方式所带来的对比因素与传统有较大的差异，明显体现出现代作曲家们对音色音响写作的特殊性与优势的捕捉。从前面的分析中可以看出:点描技法作品中的各音响元素可以在量化后形成数值序列，这些序列之间虽然在整体上不存在任何相关性，但是从局部来看，部分乐曲片段的力度值与时值等参数之间相关性很强，而相关性最强处恰好为黄金分割点和负黄金分割点的位置。这种“巧合”既可以理解为是博尔科姆有意而为之，也可以认为是潜意识中的理性安排。由此，我们可以认为在看似凌乱无章的现代音乐创作中，作曲家一方面在音色音响的并置与对比上借助更加无序的方式改变织体密度和质量来塑造不同的音乐形象，与此同时在结构上又继承着传统音乐中严谨的内在逻辑和理性思维。本论文中的量化以及音响元素对比方法不仅仅可以用来分析博尔科姆的钢琴点描作品，同样也可以应用在解析20世纪其他作曲家的作品中蕴含的各音响元素的隐性联系，以及和声、力度、时值、演奏法等发面的相互作用，为相关作品的解构分析提供了新的思路和途径。

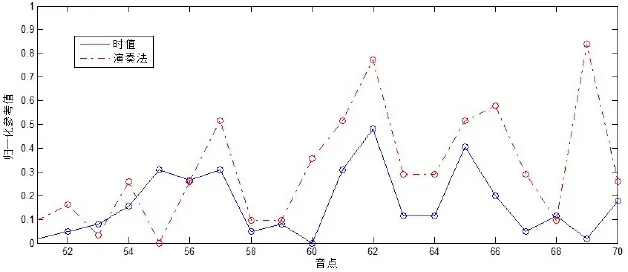
图14 时值与演奏法：第50-70音点归一化参考值

作者说明：本文为教育部人文社会科学研究规划基金项目《基于系统科学方法的钢琴教学法研究》（编号：14YJA760033）成果。

（责任编辑 张 璟）

Quantitative and Comparative Study on Sound Elements of Pointillism in William Bolcom’s Modern Piano Work: A Case Study of the First one of12 Etudes

ZHANG Fang

This paper selected the sound elements of pointillism in contemporary American composer William Bolcom piano works as the research object，with the theories of statistics and harmony mechanics to quantitative analysis the dynamics，duration，playing method and pitch parameters in the first one of12 Etudes，and then observed the material characteristics，sound development and structural layout in the work，interpreted the composer using the sound elements in the creation to realize the overall design.

William Bolcom（1938-），12 Etudes for Piano，harmony mechanics，statistics，sound elements，structure layout

J614.5

A

10.3969/j.issn1003-7721.2016.01.013

1003-7721（2016）01-0127-11

2016-01-06

张放，男，汉，中国人民大学艺术学院讲师、音乐系副主任，首都师范大学音乐学院博士研究生（北京100872）。